如果您想了解如何实现K-Means++算法?的相关知识,那么本文是一篇不可错过的文章,我们将对k-means算法的步骤进行全面详尽的解释,并且为您提供关于Golang如何实现高效的AI算法?、Java
如果您想了解如何实现K-Means ++算法?的相关知识,那么本文是一篇不可错过的文章,我们将对k-means算法的步骤进行全面详尽的解释,并且为您提供关于Golang如何实现高效的AI算法?、Java中如何实现抽奖功能的算法?、Java中如何实现插入排序算法?、Java如何实现Kruskal算法的有价值的信息。
本文目录一览:
如何实现K-Means ++算法?(k-means算法的步骤)
我无法完全了解K-Means++算法。我很感兴趣第一个k质心的选取方式,即初始化,其余的就像原始的K-Means算法一样。
- 使用的概率函数是基于距离还是高斯?
- 同时,为新质心选取了最远的距离点(与其他质心相对)。
我将逐步解释并举例说明。维基百科中的那个还不够清楚。一个注释非常好的源代码也将有所帮助。如果您使用的是6个数组,请告诉我们哪个数组适合什么。
答案1
小编典典有趣的问题。感谢您使本文引起我的注意-K-Means++:谨慎播种的优势
简而言之,聚类中心最初是从一组输入观察向量中随机选择的,x如果x不靠近任何先前选择的中心,则选择向量的可能性就很高。
这是一维示例。我们的观察值为[0,1,2,3,4]。令第一个中心c1为0。下一个聚类中心c2为x
的概率与成正比||c1-x||^2。因此,P(c2 = 1)= 1a,P(c2 = 2)= 4a,P(c2 = 3)= 9a,P(c2 = 4)=16a,其中a = 1 /(1 + 4 + 9 + 16)。
假设c2 = 4。然后,P(c3 = 1)= 1a,P(c3 = 2)= 4a,P(c3 = 3)= 1a,其中a = 1 /(1 + 4 + 1)。
我已经用Python编写了初始化过程;我不知道这是否对您有帮助。
def initialize(X, K): C = [X[0]] for k in range(1, K): D2 = scipy.array([min([scipy.inner(c-x,c-x) for c in C]) for x in X]) probs = D2/D2.sum() cumprobs = probs.cumsum() r = scipy.rand() for j,p in enumerate(cumprobs): if r < p: i = j break C.append(X[i]) return C澄清说明:的输出cumsum为我们提供了划分区间[0,1]的边界。这些分区的长度等于相应点被选择为中心的概率。因此,由于r在[0,1]之间均匀选择,因此它将恰好落入这些间隔之一(由于break)。的for循环检查以查看哪个分区r是英寸
例:
probs = [0.1, 0.2, 0.3, 0.4]cumprobs = [0.1, 0.3, 0.6, 1.0]if r < cumprobs[0]: # this event has probability 0.1 i = 0elif r < cumprobs[1]: # this event has probability 0.2 i = 1elif r < cumprobs[2]: # this event has probability 0.3 i = 2elif r < cumprobs[3]: # this event has probability 0.4 i = 3
Golang如何实现高效的AI算法?

Golang(又称Go语言)是一种现代化的、高效的编程语言,广泛应用于各个领域。在人工智能(AI)领域,高效的算法是非常重要的。本文将探讨如何使用Golang实现高效的AI算法。
为了实现高效的AI算法,首先需要对Golang的特性和优势有所了解。Golang是一种编译型语言,使用静态类型系统,具有垃圾回收功能。它的设计目标之一就是提供高效的并发支持。这些特性使得Golang成为实现高性能、高并发的AI算法的理想选择。
第一步是选择适合AI的Golang库。Golang拥有丰富的开源库,包括用于数据处理、机器学习和神经网络的库。例如,Gonum是一个专门用于数学和统计的库,提供了许多常用的线性代数和概率分布函数。GoCV可以用于图像处理和计算机视觉。而Gorgonia和Golearn则是用于机器学习的库,提供了各种常见的机器学习算法和工具。
然后,需要考虑如何利用并发性来提高AI算法的效率。Golang的并发模型采用goroutine和channel,非常适合解决并行计算的问题。可以将AI算法中的独立任务分解成多个goroutine,并使用channel在它们之间传递数据。这样可以充分利用多核处理器的性能,并提高算法的运行效率。此外,还可以使用Golang的互斥锁(mutex)和条件变量(condition)机制来管理和保护共享的资源,确保多个goroutine之间能够正确地协调和同步。
立即学习“go语言免费学习笔记(深入)”;
另一个关键因素是优化数据处理和算法实现。Golang提供了丰富的数据结构和算法库,可以帮助实现高效的数据处理。例如,使用切片(slice)来处理大规模数据集,而不是使用传统的数组。切片可以动态扩展和缩小,减少了内存的浪费。此外,可以使用map来实现高效的数据索引和查询。对于一些计算密集型的算法,可以使用Golang的内联函数和汇编插入(inlining and assembly)功能,进一步提高算法的性能。
最后,必须进行充分的性能调优和测试,以确保算法在实际应用中的高效性。Golang提供了丰富的性能分析和性能测试工具,可以帮助发现和修复性能瓶颈。使用这些工具,可以测量算法的运行时间、内存使用情况和并发性能等指标,并进行比较和优化。
总而言之,Golang是一种完美的选择,用于实现高效的AI算法。它的并发性能和丰富的开源库使其成为一个有效的工具,可以加速AI算法的开发和部署。但是,在开始使用Golang时,需要对其特性和优势有所了解,并进行合理的数据处理和算法实现。通过优化和测试,可以确保算法能够在实际应用中实现高效和高性能。
以上就是Golang如何实现高效的AI算法?的详细内容,更多请关注php中文网其它相关文章!

Java中如何实现抽奖功能的算法?
一、题目描述
题目: 小虚竹为了给粉丝送福利,决定在参与学习打卡活动的粉丝中抽一位幸运粉丝,送份小礼物。为了公平,要保证抽奖过程是随机的。
二、解题思路
1、把参与的人员加到集合中
2、使用Random对象获取随机数
3、把随机数当下标,获取集合中的幸运用户
三、代码详解
public class Basics28 {
public static void main(String[] args) {
List<String> luckUserNames = getLuckUserNames();
Random random = new Random();
int luckNum = random.nextInt(6);
System.out.println("幸运的未来大佬是:"+luckUserNames.get(luckNum));
}
private static List<String> getLuckUserNames(){
List<String> luckUserNames = new ArrayList<String>();
luckUserNames.add("李慢慢_");
luckUserNames.add("TryAgain-");
luckUserNames.add("team_dog");
luckUserNames.add("Jasonakeke");
luckUserNames.add("学好c语言的小王同学");
luckUserNames.add("Ara~追着风跑");
return luckUserNames;
}
}
立即学习“Java免费学习笔记(深入)”;
四、优化抽奖算法
解题思路
随机次数太少,需要优化
需要列出所有人随机命中的次数,显示出来,比较公开公平
代码详解
public class LuckDraw {
public static void main(String[] args) {
List<String> luckUserNames = getLuckUserNames();
Random random = new Random();
//key:luckNum ,value:count
Map<Integer,Integer> luckNumMap = new HashMap<Integer, Integer>();
for (int i = 0; i < 100; i++) {
int luckNum = random.nextInt(4);
Integer count = luckNumMap.get(luckNum);
if(count==null){
count = 0;
}
++count;
luckNumMap.put(luckNum,count);
}
Integer maxLuckNum = 0;
Integer maxCount =0;
for(Integer luckNum:luckNumMap.keySet()){
if(maxCount<luckNumMap.get(luckNum)){
maxCount = luckNumMap.get(luckNum);
maxLuckNum = luckNum;
}
System.out.println(luckUserNames.get(luckNum)+"同学的幸运值:"+luckNumMap.get(luckNum));
}
System.out.println("本周学习打卡积分第一且是幸运的未来大佬是:"+luckUserNames.get(maxLuckNum));
}
private static List<String> getLuckUserNames(){
List<String> luckUserNames = new ArrayList<String>();
luckUserNames.add("学好c语言的小王同学");
luckUserNames.add("Ara~追着风跑");
luckUserNames.add("李慢慢_");
luckUserNames.add("Jasonakeke");
return luckUserNames;
}
}
以上就是Java中如何实现抽奖功能的算法?的详细内容,更多请关注php中文网其它相关文章!

Java中如何实现插入排序算法?
一、基本思想
插入排序(insertion-sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
二、算法分析
1、算法描述
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
从第一个元素开始,该元素可以认为已经被排序;
取出下一个元素,在已经排序的元素序列中从后向前扫描;
-
如果该元素(已排序)大于新元素,将该元素移到下一位置;
立即学习“Java免费学习笔记(深入)”;
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
将新元素插入到该位置后;
重复步骤2~5。
2、过程分析
(1)、将第一个元素 (1) 标记为已经排序过。
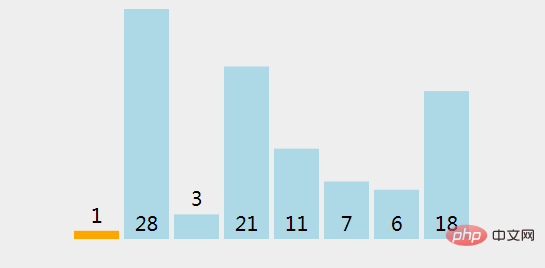
(2)、提取第一个没有排序过的元素 (28)。
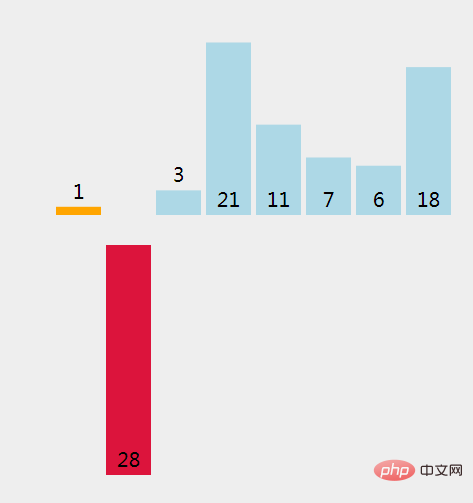
(3)、找出插入提取元素的地方;和已经排序过的元素 1 比较。
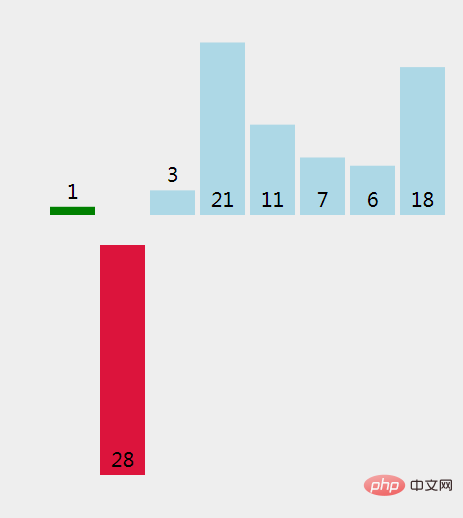
(4)、1 > 28 不成立(False), 在现有位置上插入一个元素。
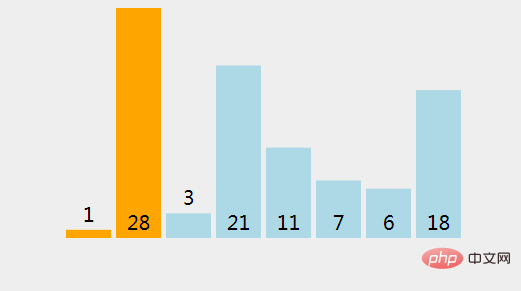
(5)、找出插入提取元素的地方;和已经排序过的元素 28 比较。
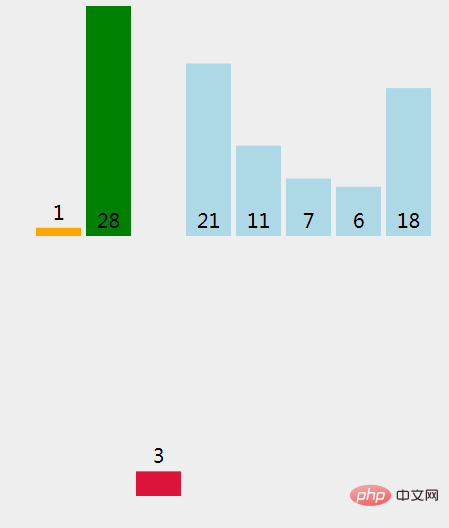
(6)、28 > 3 成立(True), 则将现在已经排序过的元素({val1}) 向右移动1格。
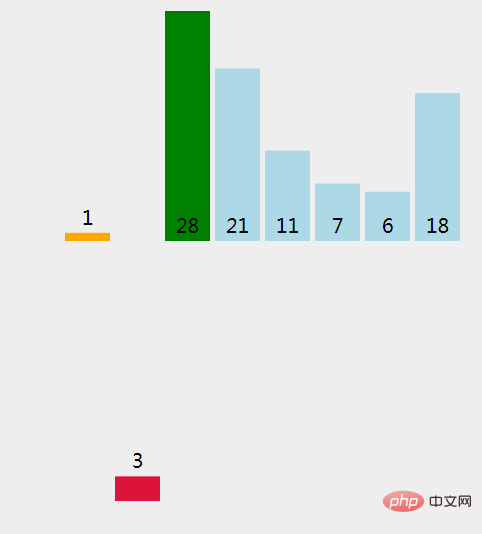
(7)、找出插入提取元素的地方;和已经排序过的元素 1 比较。
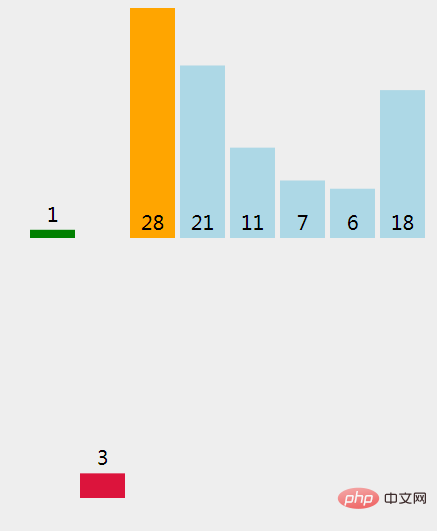
(8)、1 > 3 不成立(False), 在现有位置上插入一个元素。
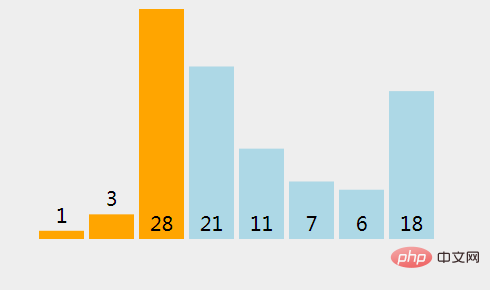
(9)、以此类推
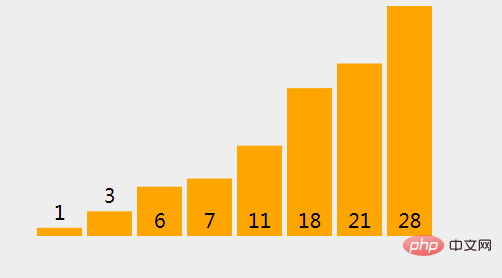
三、算法实现
package com.algorithm.tenSortingAlgorithm;
import java.util.Arrays;
public class InsertionSort {
private static void insertionSort(int[] arr) {
int preIndex, current;
for (int i = 1; i < arr.length; i++) {
preIndex = i - 1;
current = arr[i];
while (preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = current;
}
}
public static void main(String[] args) {
int[] arr = {1,28,3,21,11,7,6,18};
insertionSort(arr);
System.out.println(Arrays.toString(arr));
}
}以上就是Java中如何实现插入排序算法?的详细内容,更多请关注php中文网其它相关文章!

Java如何实现Kruskal算法
介绍
构造最小生成树还有一种算法,即 kruskal 算法:设图 g=(v,e)是无向连通带权图,v={1,2,...n};设最小生成树 t=(v,te),该树的初始状态只有 n 个节点而无边的非连通图t=(v,{}),kruskal 算法将这n 个节点看成 n 个孤立的连通分支。它首先将所有边都按权值从小到大排序,然后值要在 t 中选的边数不到 n-1,就做这样贪心选择:在边集 e 中选择权值最小的边(i,j),如果将边(i,j)加入集合 te 中不产生回路,则将边(i,j)加入边集 te 中,即用边(i,j)将这两个分支合并成一个连通分支;否则继续选择下一条最短边。把边(i,j)从集合 e 中删去,继续上面的贪心选择,直到 t 中的所有节点都在同一个连通分支上为止。此时,选取的 n-1 条边恰好构成图 g 的一棵最小生成树 t。
Kruskal 算法用一种非常聪明的方法,就是运用集合避圈;如果所选择加入边的起点和终点都在 T 集合中,就可以断定会形成回路,变的两个节点不能属于同一个集合。
算法步骤
1 初始化。将所有边都按权值从小到大排序,将每个节点集合号都初始化为自身编号。
2 按排序后的顺序选择权值最小的边(u,v)。
立即学习“Java免费学习笔记(深入)”;
3 如果节点 u 和 v 属于两个不同的连通分支,则将边(u,v)加入边集 TE 中,并将两个连通分支合并。
4 如果选取的边数小于 n-1,则转向步骤2,否则算法结束。
一、构建后的图
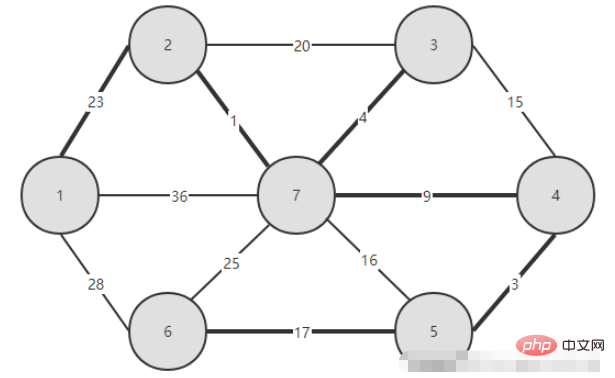
二、代码
package graph.kruskal;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
public class Kruskal {
static final int N = 100;
static int fa[] = new int[N];
static int n;
static int m;
static Edge e[] = new Edge[N * N];
static List<Edge> edgeList = new ArrayList();
static {
for (int i = 0; i < e.length; i++) {
e[i] = new Edge();
}
}
// 初始化集合号为自身
static void Init(int n) {
for (int i = 1; i <= n; i++)
fa[i] = i;
}
// 合并
static int Merge(int a, int b) {
int p = fa[a];
int q = fa[b];
if (p == q) return 0;
for (int i = 1; i <= n; i++) { // 检查所有结点,把集合号是 q 的改为 p
if (fa[i] == q)
fa[i] = p; // a 的集合号赋值给 b 集合号
}
return 1;
}
// 求最小生成树
static int Kruskal(int n) {
int ans = 0;
Collections.sort(edgeList);
for (int i = 0; i < m; i++)
if (Merge(edgeList.get(i).u, edgeList.get(i).v) == 1) {
ans += edgeList.get(i).w;
n--;
if (n == 1)//n-1次合并算法结束
return ans;
}
return 0;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
Init(n);
for (int i = 1; i <= m; i++) {
e[i].u = scanner.nextInt();
e[i].v = scanner.nextInt();
e[i].w = scanner.nextInt();
edgeList.add(e[i]);
}
System.out.println("最小的花费是:" + Kruskal(n));
}
}
class Edge implements Comparable {
int u;
int w;
int v;
@Override
public int compareTo(Object o) {
if (this.w > ((Edge) o).w) {
return 1;
} else if (this.w == ((Edge) o).w) {
return 0;
} else {
return -1;
}
}
}三、测试
绿色为输入,白色为输出。
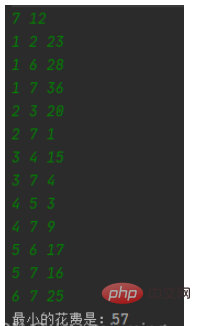
以上就是Java如何实现Kruskal算法的详细内容,更多请关注php中文网其它相关文章!
今天关于如何实现K-Means ++算法?和k-means算法的步骤的讲解已经结束,谢谢您的阅读,如果想了解更多关于Golang如何实现高效的AI算法?、Java中如何实现抽奖功能的算法?、Java中如何实现插入排序算法?、Java如何实现Kruskal算法的相关知识,请在本站搜索。
本文标签:





