在这篇文章中，我们将为您详细介绍R语言实现支持向量机SVM应用案例的内容，并且讨论关于r语言支持向量机代码的相关问题。此外，我们还会涉及一些关于3.SVM支持向量机、ML--支持向量机SVM、NLP自
在这篇文章中，我们将为您详细介绍R语言实现支持向量机SVM应用案例的内容，并且讨论关于r语言支持向量机代码的相关问题。此外，我们还会涉及一些关于3.SVM支持向量机、ML--支持向量机SVM、NLP自然语言处理系列5-支持向量机(SVM)、OpenCV 学习笔记 07 支持向量机SVM（flag）的知识，以帮助您更全面地了解这个主题。
本文目录一览：- R语言实现支持向量机SVM应用案例（r语言支持向量机代码）
- 3.SVM支持向量机
- ML--支持向量机SVM
- NLP自然语言处理系列5-支持向量机(SVM)
- OpenCV 学习笔记 07 支持向量机SVM（flag）
R语言实现支持向量机SVM应用案例（r语言支持向量机代码）
IRIS数据集简介
IRIS数据集中的数据源于1936年费希尔法发表的一篇论文。彼时他收集了三种鸢尾花（分别标记为setosa、versicolor和virginical）的花萼和花瓣数据。包括花萼的长度和宽度，以及花瓣的长度和宽度。我们将根据这四个特征来建立支持向量机模型从而实现对三种鸢尾花的分类判别任务。
有关数据可以从datasets软件包中的iris数据集里获取，下面我们演示性地列出了前5行数据。成功载入数据后，易见其中共包含了150个样本（被标记为setosa、versicolor和virginica的样本各50个），以及四个样本特征，分别是Sepal.Length、Sepal.Width、Petal.Length和Petal.Width。
> iris
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
7 4.6 3.4 1.4 0.3 setosa
8 5.0 3.4 1.5 0.2 setosa
9 4.4 2.9 1.4 0.2 setosa
10 4.9 3.1 1.5 0.1 setosa
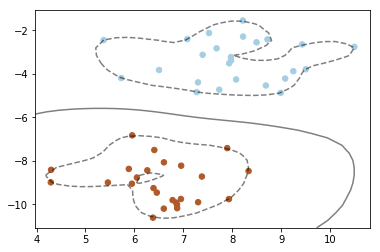
在正式建模之前，我们也可以通过一个图型来初步判定一下数据的分布情况，为此在R中使用如下代码来绘制（仅选择Petal.Length和Petal.Width这两个特征时）数据的划分情况。
library(lattice)
xyplot(Petal.Length ~ Petal.Width, data = iris,
groups = Species,
auto.key = list(corner=c(1, 0)))
上述代码的执行结果如图14-13所示，从中不难发现，标记为setosa的鸢尾花可以很容易地被划分出来。但仅使用Petal.Length和Petal.Width这两个特征时，versicolor和virginica之间尚不是线性可分的。
函数svm()在建立支持向量机分类模型时有两种方式。第一种是根据既定公式建立模型，此时的函数使用格式为：
svm(formula, data= NULL, subset, na.action = na.omit , scale= TRUE)
其中:
- formula表示函数模型的形式
- data表示在模型中包含的有变量的一组可选格式数据
- 参数na.action用于指定当样本数据中存在无效的空数据时系统应该进行怎样的处理。默认值na.omit表示程序会忽略那些数据缺失的样本。另外一个可选的赋值为na.fail，它指示系统在遇到空数据时给出一条错误信息。
- 参数scale为一个逻辑向量指定特征是护具是否需要标准化（默认标准化为均值0，方差1）
- 索引向量subset用于指定那些将来将被用来训练模型的采样数据。
例如，已经知道仅用Petal.Length和Petal.Width这两个特征时标记为setosa和versicolor的鸢尾花是线性可分的，所以我们用下面的代码来构建SVM模型：
data(iris)
attach(iris)
subdata <- iris[iris$Species != ''virginica'', ]
subdata$Speices <- factor(subdata$Species)
model1 <- svm(Species ~ Petal.Length + Petal.Width,
data = subdata)
plot(model1, subdata, Petal.Length ~ Petal.Width)
绘制的模型如下:
在使用第一种格式建立模型时，若使用数据中的全部特征变量作为模型特征变量时，可以简要地使用“Species~．”中的“．”代替全部的特征变量。例如下面的代码就利用了全部四种特征来对三种鸢尾花进行分类。
model2 <- svm(Species~., data = iris) summary(model2)
summary函数的结果如下：
> model2 <- svm(Species~., data = iris)
> summary(model2)
Call:
svm(formula = Species ~ ., data = iris)
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
gamma: 0.25
Number of Support Vectors: 51
( 8 22 21 )
Number of Classes: 3
Levels:
setosa versicolor virginica
通过summary函数可以得到关于模型的相关信息。
- 其中，SVM-Type项目说明本模型的类别为C分类器模型；
- SVM-Kernel项目说明本模型所使用的核函数为高斯内积函数且核函数中参数gamma的取值为0.25；
- cost项目说明本模型确定的约束违反成本为1；
- 此外我们可以看到，模型找到了51个支持向量：第一类包含有8个支持向量，第二类包含有22个支持想想，第三类包含21个支持向量。
- 最后一行说明模型中的三个类别分别为setosa、versicolor和virginica。
第二种使用svm()函数的方式则是根据所给的数据建立模型。这种方式形式要复杂一些，但是它允许我们以一种更加灵活的方式来构建模型。它的函数使用格式如下（注意我们仅列出了其中的主要参数）。
svm(x, y = NULL, scale = TRUE, type = NULL, kernel = "radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x), coef0 = 0, cost = 1, nu = 0.5, subset, na.action = na.omit)
其中：
- x可以是一个数据矩阵，也可以是一个数据向量，同时也可以是一个稀疏矩阵。y是对于x数据的结果标签，它既可以是字符向量也可以为数值向量。x和y共同决定了将要用来建模的训练数据以及模型的积分形式。
- 参数type用于指定建立模型的类别。支持向量机模型通常可以用作分类模型、回归模型和异常检查模型。根据用途的不同，在svm函数中的type可取的值为C-classification、nu-classification、one-classification、eps-regression和nu-regression这五种类型。其中前三种是针对于字符结果变量的分类方式，其中第三种方式为逻辑判别，即判别结果输出所需判别样本是否属于该类别。而后两种则是针对数值型结果变量的分类方式。
- kernel是指在模型的建立过程中使用的核函数。针对线性不可分的问题，为了提高模型预测精度，通常会只用核函数对原始数据进行变换，提高原始特征维度，解决支持向量机模型线性不可分的问题。svm函数中kernel参数有四个可选核函数，分别为线性核函数、多项式核函数、高斯核函数及神经网络核函数。其中，高斯核函数与多项式核函数被认为是性能最好、也是最常用的核函数。
核函数有两种主要类型：局部性核函数和全局性核函数，高斯核函数是一个典型的局部性核函数，而多项式核函数则是一个典型的全局性核函数。局部性核函数仅仅在测试点附近小邻域内对数据点有影响，其学习能力强，泛化性能较弱；而全局性核函数则相对来说泛化性能较强，学习能力较弱。
- 对于选定的核函数，degree参数是指核函数多项式内积函数中的参数，其默认值为3。gamma参数给出了一个核函数中除线性内积函数以外的所有函数的参数，默认值为1.coef0参数是指核函数中多项式内积函数sigmoid内积函数的中的参数，默认值为0.
- 参数cost是软间隔模型中离群点权重。
- 最后，参数nu是用于nu-regression、nu-classification和one-classification类型中的参数。
一个经验性的结论为，在利用svm函数建立支持向量机模型时，使用标准化后的数据建立的模型效果更好。根据函数的第二种使用格式，在针对上述数据建立模型时，首先应该将结果变量和特征变量分别提取出来。结果向量用一个向量表示，特征向量用一个矩阵表示。在确定好数据后还应根据数据分析所使用的核函数以及核函数所对应的参数值，通常默认使用高斯内积函数作为核函数。下面给出一段实例代码：
# 提取iris数据集中除第五列以外的数据作为特征变量
x <- iris[, -5]
# 提取iris数据集中第五列数据作为结果变量
y <- iris[, 5]
model3 <- svm(x, y, kernel = "radial",
gamma = if (is.vector(x)) 1 else 1 / ncol(x))
在使用第二种格式建立模型时，不需要特别强调所建立模型的形式，函数会自动将所有输入的特征变量数据作为建立模型所需要的特征向量。在上述过程中，确定核函数的gamma系数时所使用的代码代表的意思为：如果特征向量是向量则gamma值取1，否则gamma值为特征向量个数的倒数。
在利用样本数据建立模型之后，我们便可以利用模型来进行相应的预测和判别。基于svm函数建立的模型来进行预测时，可以选用函数predict函数来完成相应的工作。在使用该函数时，应该首先确认将要用于预测的样本数据，并将样本数据的特征变量整合后放入同一个矩阵。代码如下：
pred <- predict(model3, x) table(pred, y)
输出结果：
> pred <- predict(model3, x)
> table(pred, y)
y
pred setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 2
virginica 0 2 48
通常在进行预测之后，还需要检查模型预测的准确程度，这时便需要使用函数table来对预测结果和真实结果做出对比展示。从上述代码的输出中，可以看到在模型预测时，模型将所有属于setosa类型的鸢尾花全部预测正确；模型将数据versicolor类型的鸢尾花中有48朵预测正确，另外两朵错误的预测为virginica类型；同样，模型将属于virginica类型的鸢尾花中的48朵预测正确，但也将另外两朵错误的预测为versicolor类型。
函数predict中的一个可选参数是decision.values，在默认情况下，该参数的缺省值为FALSE。若将其值置为TRUE，那么函数的返回值中将包含有一个名为decision.values的属性，该属性是一个n*c的矩阵。这里，n是被预测的数据量，c是一个二分类器的决策值。注意，因为我们使用支持向量机对样本数据进行分类，分类结果可能是有k个类别。那么这k个类别中任意两类之间都会有一个二分类器。所以，我么可以推断出总共的二分类器数量为K(k-1)/2。决策值矩阵中的列名就是二分类器的标签。代码如下：
pred <- predict(model3, x, decision.values = TRUE) attr(pred, "decision.values")[1:4, ]
输出如下：
> pred <- predict(model3, x, decision.values = TRUE)
> attr(pred, "decision.values")[1:4, ]
setosa/versicolor setosa/virginica
1 1.196152 1.091757
2 1.064621 1.056185
3 1.180842 1.074542
4 1.110699 1.053012
versicolor/virginica
1 0.6708810
2 0.8483518
3 0.6439798
4 0.6782041
由于我们处理的是一个分类问题。所以分类决策最终是经由一个sign()函数来完成的。从上面的输出中可以看到，对于样本数据4而言，标签setosa/versicolor对应的值大于0，因此属于setosa类；标签setosa/virginica对应的值同样大于0，因此数据setosa类；在二分类器versicolor/virginica中对应的决策值大于0，判定属于versicolor类。所以，最终样本数据4被判定数据setosa类。
可视化模型，代码如下：
> plot(cmdscale(dist(iris[,-5])),
+ col=c("orange", "blue", "green")[as.integer(iris[,5])],
+ pch=c("o", "+")[1:150 %in% model3$index + 1])
>
> # ?legend
> legend(1.8, -0.5, c("setosa","versicolor", "virgincia"),
+ col = c("orange","blue","green"), lty = 1,
+ cex = 0.6,
+ bty = "o", box.lty = 1, box.col = "black")
在图中我们可以看到，鸢尾花中的第一种setosa类别同其他两种区别较大，而剩下的versicolor类别和virginica类别却相差很小，甚至存在交叉难以区分。注意，这是在使用了全部四种特征之后仍然难以区分的。这也从另一个角度解释了在模型预测过程中出现的问题，所以模型误将2朵versicolor 类别的花预测成了virginica 类别，而将2朵virginica 类别的花错误地预测成了versicolor 类别，也就是很正常现象了。
到此这篇关于R语言实现支持向量机SVM应用案例的文章就介绍到这了,更多相关R语言支持向量机SVM内容请搜索以前的文章或继续浏览下面的相关文章希望大家以后多多支持！
- R语言删除/添加数据框中的某一行/列
- R语言数据框合并(merge)的几种方式小结
- R语言学习笔记之lm函数详解
- R语言利用loess如何去除某个变量对数据的影响详解
- R语言strsplit函数用法深入详解
- R语言实现对数据框按某一列分组求组内平均值
- 解决R语言安装时出现辑程包不存在的问题
3.SVM支持向量机
思想：找一条曲线，使得所有样本点到这条曲线的距离的最小值最大
点x到直线的距离：
$$ l = \frac{1}{{\left\| w \right\|}}({w^T}x + b) $$
对于二分类，y取值只有-1和1，那么同号表示分类正确，异号表示分类错误。在感知算法中，这样的超平面会有多个要找到最好的一个。
几何间隔：$\widehat {{y_i}} = {y_i}({w^T}{x_i} + b)$
函数间隔：$\widehat {{y_i}} = {y_i}\frac{1}{{\left\| w \right\|}}({w^T}{x_i} + b)$
可以看到说w，b同时扩大超平面是不变的，有：
$$ \mathop {\max }\limits_{w,b} \widehat y\& \& {y_i}({w^T}{x_i} + b) \ge \widehat y,i = 1,2,...,m $$
由于$\widehat y$取值不会影响w,b，因此取$\widehat y=1$，引入松弛变量：
$$ \begin{array}{l} \mathop {\min }\limits_{w,b,\xi } \left\| w \right\| + c\sum\limits_{i = 1}^m {{\xi _i}} \\ s.t.{y_i}({w^T}{x_i} + b) \ge 1 - {\xi _i},i = 1,2,...,m \end{array} $$
然后用拉格朗日乘数法，转换成无约束问题，用SMO进行求解。
ML--支持向量机SVM
ML–支持向量机SVM
SVM算法专门解决线性不可分
主要涉及的知识点有：
- 支持向量机的基本原理和构造
- 支持向量机的核函数
- 支持向量机的参数调节
- 支持向量机实例–对波士顿房价进行回归分析
一.支持向量机SVM基本概念
1.支持向量机SVM的原理
# 导入numpy
import numpy as np
# 导入画图工具
import matplotlib.pyplot as plt
# 导入支持向量机SVM
from sklearn import svm
# 导入数据集生成工具
from sklearn.datasets import make_blobs
# 先创建50个数据点，让它们分为两类
X,y=make_blobs(n_samples=50,centers=2,random_state=6)
# 创建一个线性内核的支持向量机模型
clf=svm.SVC(kernel=''linear'',C=1000)
clf.fit(X,y)
# 把数据点画出来
plt.scatter(X[:,0],X[:,1],c=y,s=30,cmap=plt.cm.Paired)
# 建立图像坐标
ax=plt.gca()
xlim=ax.get_xlim()
ylim=ax.get_ylim()
# 生成两个等差数列
xx=np.linspace(xlim[0],xlim[1],30)
yy=np.linspace(ylim[0],ylim[1],30)
YY,XX=np.meshgrid(yy,xx)
xy=np.vstack([XX.ravel(),YY.ravel()]).T
Z=clf.decision_function(xy).reshape(XX.shape)
# 把分类的决定边界画出来
ax.contour(XX,YY,Z,colors=''k'',levels=[-1,0,1],alpha=0.5,linestyles=[''--'',''-'',''--''])
ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=100,linewidth=1,facecolors=''none'')
plt.show()
[结果分析] 从图中，可以清晰地看到，在分类器两侧分别有两条虚线，那些正好压在虚线上的数据点，就是我们刚刚提到的支持向量。而上例使用的这种方法称为最大边界间隔超平面(Maximum Margin Separating Hyperplane)。指的是说中间这条实线(在高维数据中是一个超平面)，和所有支持向量之间的距离，都是最大的
如果我们把SVM的内核换成是RBF，看下结果
# 创建一个RBF内核的支持向量机模型
clf_rbf=svm.SVC(kernel=''rbf'',C=1000)
clf_rbf.fit(X,y)
# 把数据点画出来
plt.scatter(X[:,0],X[:,1],c=y,s=30,cmap=plt.cm.Paired)
# 建立图像坐标
ax=plt.gca()
xlim=ax.get_xlim()
ylim=ax.get_ylim()
# 生成两个等差数列
xx=np.linspace(xlim[0],xlim[1],30)
yy=np.linspace(ylim[0],ylim[1],30)
YY,XX=np.meshgrid(yy,xx)
xy=np.vstack([XX.ravel(),YY.ravel()]).T
Z=clf_rbf.decision_function(xy).reshape(XX.shape)
# 把分类的决定边界画出来
ax.contour(XX,YY,Z,colors=''k'',levels=[-1,0,1],alpha=0.5,linestyles=[''--'',''-'',''--''])
ax.scatter(clf_rbf.support_vectors_[:,0],clf_rbf.support_vectors_[:,1],s=100,linewidth=1,facecolors=''none'')
plt.show()
[结果分析] 我们看到分类器的样子变得完全不一样了，这是因为当我们使用RBF内核的时候，数据点之间的距离是用如下公式来计算的：
公式中的x1和x2代表两个不同的数据点，而|||x1-x2|代表两个点之间的欧几里得距离。γ(gamma)是用来控制RBF内核宽度的参数，也就是图中实线距离两条虚线的距离
二.SVM的核函数与参数选择
1.不同核函数的SVM对比
前面提到的linearSVM就是一种使用了线性内核的SVM算法。不过linearSVM不支持对核函数进行修改，因为它默认只能使用线性内核。为了让大家能够直观体验不同内核的SVM算法在分类中的表现，我们画个图像进行展示
# 导入红酒数据集
from sklearn.datasets import load_wine
# 定义一个函数用来画图
def make_meshgrid(x,y,h=.02):
x_min,x_max=x.min()-1,x.max()+1
y_min,y_max=y.min()-1,y.max()+1
xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))
return xx,yy
# 定义一个绘制等高线的函数
def plot_contours(ax,clf,xx,yy,**params):
Z=clf.predict(np.c_[xx.ravel(),yy.ravel()])
Z=Z.reshape(xx.shape)
out=ax.contourf(xx,yy,Z,**params)
return out
# 使用酒的数据集
wine=load_wine()
# 选取数据集的前两个特征
X=wine.data[:,:2]
y=wine.target
C=1.0 # 选取数据集的前两个特征
models=(svm.SVC(kernel=''linear'',C=C),svm.LinearSVC(C=C),svm.SVC(kernel=''rbf'',gamma=0.7,C=C),svm.SVC(kernel=''poly'',degree=3,C=C))
models=(clf.fit(X,y) for clf in models)
# 设定图题
titles=(''SVC with linear kernel'',''LinearSVC (linear kernel)'',''SVC with RBF kernel'',''SVC with polynomial (degree 3) kernel'')
# 设定一个字图形的个数和排列方式
fit,sub=plt.subplots(2,2)
plt.subplots_adjust(wspace=0.4,hspace=0.4)
# 使用前面定义的函数进行画图
X0,X1=X[:,0],X[:,1]
xx,yy=make_meshgrid(X0,X1)
for clf,title,ax in zip(models,titles,sub.flatten()):
plot_contours(ax,clf,xx,yy,cmap=plt.cm.plasma,alpha=0.8)
ax.scatter(X0,X1,c=y,cmap=plt.cm.plasma,s=20,edgecolors=''k'')
ax.set_xlim(xx.min(),xx.max())
ax.set_ylim(yy.min(),yy.max())
ax.set_xlabel(''Feature 0'')
ax.set_ylabel(''Feature 1'')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
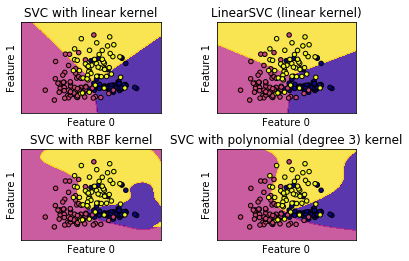
[结果分析] 我们可以看到线性内核的SVC与linearSVC得到的结果非常近似，但仍然有一点点差别。其中一个原因是linearSVC对L2范数进行最小化，而线性内核的SVC是对L1范数进行最小化。无论如何，linearSVC和线性内核的SVC生成的决定边界都是线性的，在更高维数据集中将会是相交的超平面。而RBF内核的SVC和polynomial内核的SVC分类器的决定边界则完全不是线性的，它们更加弹性。而决定了它们决定边界形状的，就是它们的参数。在polynomial内核的SVC中，起决定性作用的参数就是degree和正则化参数C，在本例中我们使用的degree为3，也就是对原始数据集的特征进行乘3次方操作。而在RBF内核的SVC中，其起决定作用的是正则化参数C和参数gamma
接下来我们重点介绍一下RBF内核SVC的gamma参数调节
2.支持向量机的gamma参数调节
首先让我们看一下不同的gamma值对于RBF内核的SVC分类器有什么影响
C=1.0 # SVM正则化参数
models=(svm.SVC(kernel=''rbf'',gamma=0.1,C=C),svm.SVC(kernel=''rbf'',gamma=1,C=C),svm.SVC(kernel=''rbf'',gamma=10,C=C))
models=(clf.fit(X,y) for clf in models)
# 设定图题
titles=(''gamma=0.1'',''gamma=1'',''gamma=10'')
# 设置子图形个数和排列
fig,sub=plt.subplots(1,3,figsize=(10,3))
X0,X1=X[:,0],X[:,1]
xx,yy=make_meshgrid(X0,X1)
# 使用定义好的函数进行画图
for clf,title,ax in zip(models,titles,sub.flatten()):
plot_contours(ax,clf,xx,yy,cmap=plt.cm.plasma,alpha=0.8)
ax.scatter(X0,X1,c=y,cmap=plt.cm.plasma,s=20,edgecolors=''k'')
ax.set_xlim(xx.min(),xx.max())
ax.set_ylim(yy.min(),yy.max())
ax.set_xlabel(''Feature 0'')
ax.set_ylabel(''Feature 1'')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
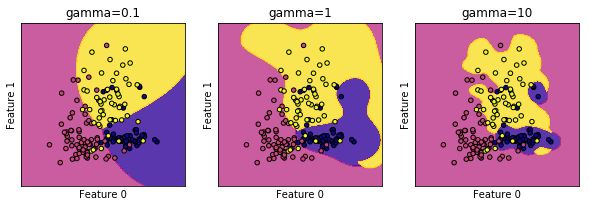
[结果分析] 从图中可以看出，自左到右gamma值从0.1增加到10，gamma值越小，则RBF内核的直径越大，这样就会有更多的点被模型圈进决定边界中，所以决定边界也就越平滑，这时的模型也就越简单；而随着参数的增加，模型则更倾向于把每个点都放到相应的决定边界中，这时模型的复杂度也相应提高了。所以gamma值越小模型越倾向于欠拟合，而gamma值越大，则模型越倾向于出现过拟合的问题
而至于正则化参数C，C值越小，模型就越受限，也就是说单个数据点对模型的影响越小，模型就越简单；而C值越大，每个数据点对模型的影响就越大，模型也会更加复杂
3.SVM算法的优势与不足
SVM应对高维数据集和低维数据集都还算是得心应手。但是，前提条件是数据集的规模不太大。如果数据集中的样本数量在1万以内，SVM都能驾驭得了，但如果样本数量超过10万的话，SVM就会非常耗费时间和内存
SVM还有一个短板，就是对于数据预处理和参数调节要求非常高
在SVM算法中，有3个参数是比较重要的：第一个是核函数的选择；第二个是核函数的参数，例如RBF的gamma值；第三个是正则化参数C。RBF内核的gamma值是用来调节内核宽度的，gamma值和C值一起控制模型的复杂度，数值越大模型越复杂，而数值越小模型越简单
三.SVM实例–波士顿房价回归分析
在scikit-learn中，内置了一个非常适合做回归分析的数据集–波士顿房价数据集。我们将使用该数据集讲解SVM中用于回归分析的SVR的用法
1.初步了解数据集
# 导入波士顿房价数据集
from sklearn.datasets import load_boston
boston=load_boston()
# 打印数据集中的键
print(boston.keys())
dict_keys([''data'', ''target'', ''feature_names'', ''DESCR'', ''filename''])
[结果分析] 从结果中可以看出，波士顿房价数据集中有5个键，分别是数据，目标，特征名称，描述和文件名。我们可能有疑问，波士顿房价数据集比红酒数据集少了一个键，就是目标名称(target_names)，这是为什么？我们查看一下
print(boston[''DESCR''])
.. _boston_dataset:
Boston house prices dataset
---------------------------
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000''s
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. ''Hedonic
prices and the demand for clean air'', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, ''Regression diagnostics
...'', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
.. topic:: References
- Belsley, Kuh & Welsch, ''Regression diagnostics: Identifying Influential Data and Sources of Collinearity'', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
[结果分析] 从上面的这段描述可以看出，数据集中共有506个样本，每个样本有13个特征变量。而后面还有一个叫作中位数的第14个变量，这个变量就是该数据集中的target
2.使用SVR进行建模
我们要先制作训练数据集和测试数据集，代码如下：
# 导入数据集拆分工具
from sklearn.model_selection import train_test_split
# 建立训练数据集和测试数据集
X,y=boston.data,boston.target
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8)
print(X_train.shape)
print(X_test.shape)
(379, 13)
(127, 13)
下面开始用SVR进行建模，我们在前面介绍了SVM的两种核函数：Linear和rbf，不过我们不知道这两种核函数哪一个会让模型表现得更好，那么分别尝试一下：
# 导入支持向量机回归模型
from sklearn.svm import SVR
# 分别测试sklearn核函数和rbf核函数
for kernel in [''linear'',''rbf'']:
svr=SVR(kernel=kernel)
svr.fit(X_train,y_train)
print(kernel,''核函数的模型训练集得分：{:.3f}''.format(svr.score(X_train,y_train)))
print(kernel,''核函数的模型测试集得分：{:.3f}''.format(svr.score(X_test,y_test)))
linear 核函数的模型训练集得分：0.709
linear 核函数的模型测试集得分：0.696
rbf 核函数的模型训练集得分：0.145
rbf 核函数的模型测试集得分：0.001
[结果分析] 两种核函数的模型得分都不能令人满意。使用rbf核函数的模型糟糕透了，在训练数据集的分只有0.145，而在测试数据集的得分完全可以用"灾难"来形容了—居然只有0.001分
这是什么原因呢？想想，会不会是数据集的各个特征之间的量级差的比较远？由于SVM算法对于数据预处理的要求是比较高的，如果数据特征量差异较大，我们需要对数据进行预处理。所以我们用可视化的方法看一看数据集中各个特征的数量级是什么情况
# 将特征数值中的最小值和最大值用散点图画出来
plt.plot(X.min(axis=0),''v'',label=''min'')
plt.plot(X.max(axis=0),''^'',label=''max'')
# 设定纵坐标为对数形式
plt.yscale(''log'')
# 设置图注位置为最佳
plt.legend(loc=''best'')
# 设定横纵轴标题
plt.xlabel(''features'')
plt.ylabel(''feature magnitude'')
# 显示图形
plt.show()
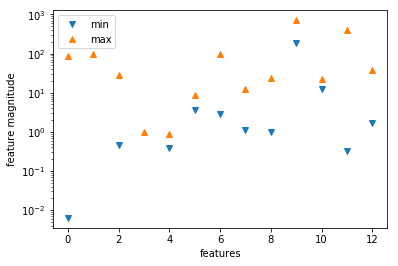
看来为了能够让SVM算法能够更好地对数据进行拟合，我们必须对数据集进行预处理
# 导入数据预处理工具
from sklearn.preprocessing import StandardScaler
# 对训练集和测试集进行数据预处理
scaler=StandardScaler()
scaler.fit(X_train)
X_train_scaled=scaler.transform(X_train)
X_test_scaled=scaler.transform(X_test)
# 将预处理后的数据特征最大值和最小值用散点图表示出来
plt.plot(X_train_scaled.min(axis=0),''v'',label=''train set min'')
plt.plot(X_train_scaled.max(axis=0),''^'',label=''train set max'')
plt.plot(X_test_scaled.min(axis=0),''v'',label=''test set min'')
plt.plot(X_test_scaled.max(axis=0),''^'',label=''test set max'')
plt.yscale(''log'')
# 设置图注位置
plt.legend(loc=''best'')
# 设置横纵轴标题
plt.xlabel(''scaled features'')
plt.ylabel(''scaled feature magnitude'')
plt.show()
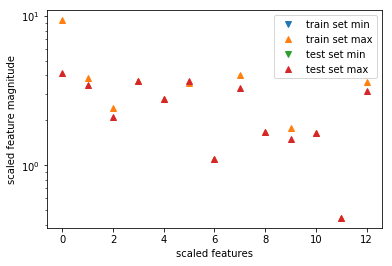
[结果分析] 经过了我们的预处理，不管是训练集还是测试集，基本上所有的特征最大值都不会超过10，而最小值也都趋于0，以至于在图中我们看不到它们了
现在我们在试试用经过预处理的数据来训练模型，看看结果会有什么不同
# 导入支持向量机回归模型
from sklearn.svm import SVR
# 分别测试sklearn核函数和rbf核函数
for kernel in [''linear'',''rbf'']:
svr=SVR(kernel=kernel)
svr.fit(X_train_scaled,y_train)
print(kernel,''核函数的模型训练集得分：{:.3f}''.format(svr.score(X_train_scaled,y_train)))
print(kernel,''核函数的模型测试集得分：{:.3f}''.format(svr.score(X_test_scaled,y_test)))
linear 核函数的模型训练集得分：0.706
linear 核函数的模型测试集得分：0.698
rbf 核函数的模型训练集得分：0.665
rbf 核函数的模型测试集得分：0.695
[结果分析] 经过预处理之后，linear内核的SVR得分变化不大，而rbf内核的SVR得分有了巨大的提升
和SVC一样，SVR模型也有gamma和C两个参数，接下来我们试着对两个参数进行修改
# 设置模型的C参数和gamma参数
svr=SVR(C=100,gamma=0.1)
svr.fit(X_train_scaled,y_train)
print(''调节参数后的模型在训练集得分：{:.3f}''.format(svr.score(X_train_scaled,y_train)))
print(''调节参数后的模型在测试集得分：{:.3f}''.format(svr.score(X_test_scaled,y_test)))
调节参数后的模型在训练集得分：0.966
调节参数后的模型在测试集得分：0.894
[结果分析] 这是一个比较不错的结果，我们看到通过参数调节，rbf内核的SVR模型在训练集的得分已经高达0.966，而在测试数据集的得分也达到了0.894，可以说现在模型的表现已经是可以接受的
NLP自然语言处理系列5-支持向量机(SVM)
1.什么是支持向量机
支持向量机（Support Vector Machine，SVM）是一种经典的分类模型，在早期的文档分类等领域有一定的应用。了解SVM的推导过程是一个充满乐趣和挑战的过程，耐心的看完整个过程，你会受益良多。所以，小Dream也决定好好讲一讲SVM的推导过程，还是跟此前一样，讲解务必追求通俗易懂，深入浅出。
首先要说的是，支持向量机最主要是用于分类。假设有一个训练样本集D={（x1,y1），（x2,y2），（x3,y3），...（xn,yn）}，支持向量机分类学习最主要的思想就是基于训练集D在样本空间中，找到一个划分超平面，将不同类别的样本分开。
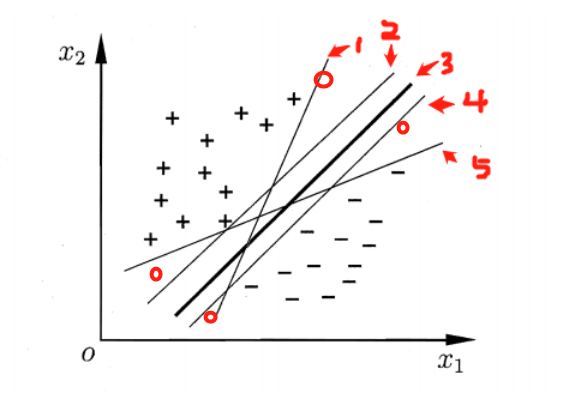
图 一 类别划分超平面
如图一所示，那些能够将+、-两类样本分开的直线（超平面），都是合理的分类器。那么，哪个分类器是最优的呢？我们可以看到，当一个新的样本（样本可能有扰动）出现在图中4个红色圆圈所在位置时，分类器1，2，4，5就极有可能把他分错。根据图一，肉眼可见，分类器3是图中的最优分类器，因为它忍受样本干扰的能力是最强的，用术语说，就是最鲁棒的。那么怎么从数学上来定义这个最优的超平面呢？
在样本空间中，假设划分超平面是这样的一个平面：
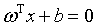（1）
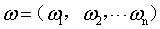称为超平面的法向量，b定义了超平面到空间远点的距离，回忆一下高中的立体几何，我们知道，超平面可以由
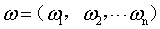和b唯一确定。那么。怎么样的一个超平面是最优的呢？
首先，我问这样一个问题，样本空间中任意一个样本，到该划分超平面的距离应该怎么表示？（赶紧回忆一下，点到平面的距离
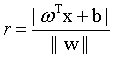（2）
我们先假设超平面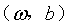
能够将所有的样本正确的进行分类。对任意
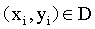如果样本属于正类，则有yi=+1，且
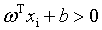；如果样本属于负类，则有yi=-1，且
。
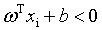我们可以选择合适的b，使得离超平面最近的哪一类点满足如下的条件：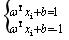
，这些点就称为支持向量。那么所有样本可以这样表示：
（3）
如图二所示，支持向量用圈圈圈住了。两个异类的支持向量的距离可以表示为：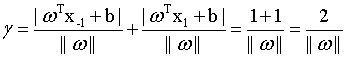
（4）
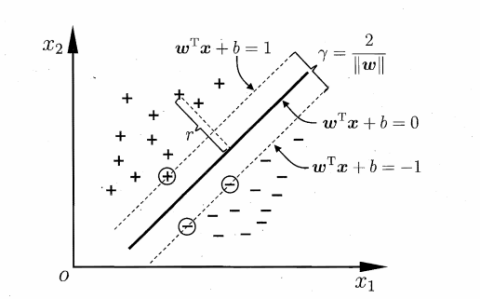图二 支持向量与间隔
那么选择最优的划分超平面就可以转为成如下的数学表达式：
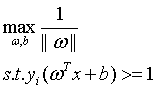(5)
为了计算简便，（5）式等价于如下：
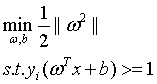（6）
怎么样，这就是SVM的基本型了，有没有感受到数学语言的魅力？简洁、明确而又优美。
2. 支持向量机如何学习
既然我们明确了SVM是个怎么样的问题，接下来要考虑的就是如何利用数据集D求得上述的超平面。
我们期望根据式6，获得一个模型：
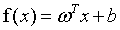(7)
式6是一个凸二次规划问题，可能会有相关的优化计算包可以求解。但是SVM有自己的更为高效的求解方式，我们来好好说一下。
求解这种带限制条件的极值问题，用的最多的应该式拉格朗日乘子法。我们对式6的每个约束条件乘以拉格朗日乘子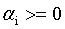
:
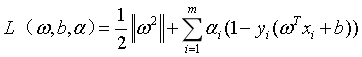(8)
其中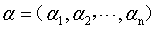
为拉格朗日乘子向量，注意向量的长度和数据集D中样本的数目相同。根据拉格朗日极值法，分别对w和b求偏导，并取极值得到：
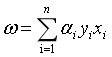(9)
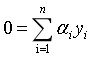(10)
将式（9）（10）带入式（8），可以得到：
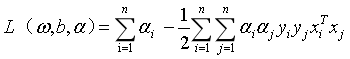
参考https://blog.csdn.net/zlsjsj/article/details/80522650
我们可以得到式6的对偶问题：
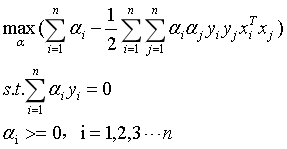(11)
这么多公式，相信大家看到都有点烦了，这里总结一下，理一理思路。
我们得到式6的SVM基本型之后，想要用一种高效的方式来求解SVM的划分超平面。在限定条件下的极值问题，我们想到了拉格朗日乘子法。通过求偏导、解极值之后，我们消去w和b，问题变成了解决式6的对偶问题式11。这样的话，求解w和b就转化成了求解拉格朗日乘子
。将所有拉格朗日乘子求出之后，就得到了模型：
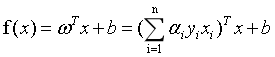
这里我们注意，拉格朗日乘子的个数与数据集样本的个数相同。
那么，式11该如何高效的求解呢？下面我们SMO（Sequential Minimal Optimization）算法就登场了。
SMO算法的基本思路是各个击破，逐个参数优化求解。具体来说就是，先选定一个参数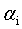
，然后固定除
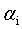之外的所有其他参数，这样就可以根据式11求极值，求得合适的
。具体来说，是这样的，先选定两个参数
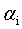和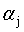
，根据式11的限制条件会有：
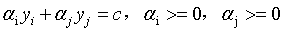(12)
其中，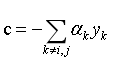
。
可以用式12将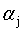
用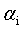
来表示，带入到式11中，得到一个关于
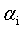的单变量二次规划（二次函数求极值）问题，就可以高效的进行求解了。
2. SVM中的核函数
上述的SVM问题的定义及求解过程中，隐含了一个假设，就是存在一个超平面，能够将两类样本分开，即问题是线性可分的。那么，如果问题不是线性可分的呢？例如，很简答的“异或”问题就是线性不可分的。
图三 线性不可分问题及其非线性映射
如图三所示，在二维空间中，没有办法找到一条直线，将“异或”问题进行正确的区分。那么如何解决线性不可分的问题呢？在图三中，将四个样本经过一个映射函数，映射到三维空间中，就可以通过一个平面将该问题划分开了。
这样我们就有了利用SVM去分类线性不可分问题的思路了。我们可以通过一个映射函数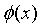
，将样本从原空间映射到高维空间，再利用上面章节的SVM原理进行分类就可以了。
下面我们再简单说一下利用升维的办法用SVM进行分类的过程。
训练样本集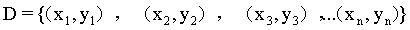
经过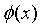
进行映射，变成了
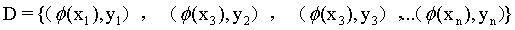，那么我们要获得这样一个模型：
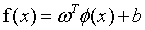（13）
在如下的限制条件下：
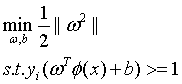（14）
同样，得到它的对偶问题：
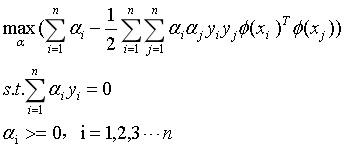（15）
同样，问题的本质并没有改变，我们其实还是可以用SMO算法求解向量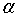
。只是多了一步，要计算
，当样本空间的维度很大时，这个计算量时很大的。为了简化计算，我们聪明的算法专家提出了核函数的概念，所谓核函数，就是为了简化上述计算而设计出来的函数，它满足如下要求：
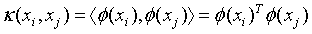（16）
那么式15就可以改写为：
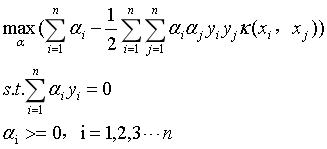（17）
我们仔细回顾下抑或问题的映射过程，可以发现，其实映射过程不是唯一的，只要满足一定的性质，映射函数可以很多，同样核函数也可以很多。
我们先列出来常用的核函数：
图四 常用核函数列表
那么，加入我们使用的高斯核，则式17可以表示为：
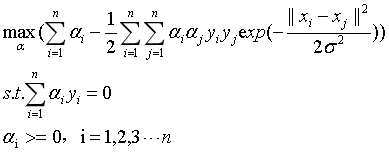（18）
我们可以看到加入核函数后，能够顺利解决线性不可分的问题，但是计算过程却并没有因此而变得复杂。
关于核函数的选择以及过拟合的处理，可以用软间隔的技术，大体的思想就是在最大化间隔的同时，允许一些样本出现在间隔里。感兴趣的同学可以出门百度一下，这里不再详述。
这篇博客可能没有太多原创的思考，但是都是小Dream根据自己的理解一个字一个字码的，可能在遣词造句上没有教科书那么严谨。但是我觉得技术博客存在意义就在于用一种朴实易懂的语言介绍一些在实际工作中非常实用的技巧、经验和技术。
---------------------------------------------------------------------------------------------------------------------------------
分享时刻：
你要记住，人生聚散起伏太常见。生命太短，铭记那些温暖与真诚吧，倒掉那些凉掉的茶水。
OpenCV 学习笔记 07 支持向量机SVM（flag）
1 SVM 基本概念
本章节主要从文字层面来概括性理解 SVM。
支持向量机（support vector machine，简SVM）是二类分类模型。
在机器学习中，它在分类与回归分析中分析数据的监督式学习模型及相关的学习算法；在给定的一组训练实例中，每个训练实例会被标记其属性类别（两个类别中的一个），是非概率的二元线性分类器。
SVM模型是将采用尽可能宽的、明显的间隔将实例分开，使得实例分属不同的空间；然后将新的实例映射到某一空间，基于新的实例所属空间来预测其类别。
SVM 除了可进行线性分类外，还可以采用核技巧进行非线性分类，将其输入隐式映射到高维特征空间中。
更正式地来说，支持向量机在高维或无限维空间中构造超平面或超平面集合，其可以用于分类、回归或其他任务。直观来说，分类边界距离最近的训练数据点越远越好，因为这样可以缩小分类器的泛化误差。
简单地说，SVM属于二类分类模型，当在平面直角坐标系中，理解为二元线性分类器，当构造高维的超平面时，可以实现非线性分类运算。
摘自维基百科 - 支持向量机
2 SVM 的数学逻辑实现过程
本章节主要是实现 SVM 的数学逻辑推导。
该部分内容主要参考内容有：
从超平面到SVM（一）
从超平面到 SVM（二）
支持向量机通俗导论（理解SVM的三层境界）
计算机视觉—人脸识别（Hog特征+SVM分类器）（8） - SVM支持向量机
支持向量机（SVM）的分析及python实现
3 SVM 的python代码实现过程
支持向量机SVM通俗理解（python代码实现）
4 SVM 的代码应用实例
关于R语言实现支持向量机SVM应用案例和r语言支持向量机代码的介绍现已完结，谢谢您的耐心阅读，如果想了解更多关于3.SVM支持向量机、ML--支持向量机SVM、NLP自然语言处理系列5-支持向量机(SVM)、OpenCV 学习笔记 07 支持向量机SVM（flag）的相关知识，请在本站寻找。
本文标签：
