本文将带您了解关于Tensorflow中的numpy随机选择的新内容，同时我们还将为您解释tensorflow随机数的相关知识，另外，我们还将为您提供关于EffectiveTensorFlowChap

本文将带您了解关于Tensorflow中的numpy随机选择的新内容，同时我们还将为您解释tensorflow随机数的相关知识，另外，我们还将为您提供关于Effective TensorFlow Chapter 4: TensorFlow中的广播Broadcast机制【转】、numpi 与 tensorflow 2.4 上的卷积、NumPy arrays and TensorFlow Tensors的区别和联系、numpy 和 tensorflow 中的各种乘法（点乘和矩阵乘）的实用信息。

本文目录一览：

• Tensorflow中的numpy随机选择（tensorflow随机数）
• Effective TensorFlow Chapter 4: TensorFlow中的广播Broadcast机制【转】
• numpi 与 tensorflow 2.4 上的卷积
• NumPy arrays and TensorFlow Tensors的区别和联系
• numpy 和 tensorflow 中的各种乘法（点乘和矩阵乘）

Tensorflow中的numpy随机选择（tensorflow随机数）

Tensorflow中是否有等效于numpy随机选择的函数。在numpy中，我们可以从给定列表中随机获得一个项目及其权重。

 np.random.choice([1,2,3,5], 1, p=[0.1, 0, 0.3, 0.6, 0])

此代码将从给定列表中选择一个权重为p的项。

答案1

小编典典

不，但是您可以使用tf.multinomial获得相同的结果：

elems = tf.convert_to_tensor([1,2,3,5])samples = tf.multinomial(tf.log([[1, 0, 0.3, 0.6]]), 1) # note log-probelems[tf.cast(samples[0][0], tf.int32)].eval()Out: 1elems[tf.cast(samples[0][0], tf.int32)].eval()Out: 5

该[0][0]部分在这里，正如multinomial预期的那样，该批次中每个元素的行都有未归一化的对数概率，并且对于样本数量还具有另一个维度。

Effective TensorFlow Chapter 4: TensorFlow中的广播Broadcast机制【转】

本文转载自：https://blog.csdn.net/LoseInVain/article/details/78763303

TensorFlow支持广播机制（Broadcast），可以广播元素间操作(elementwise operations)。正常情况下，当你想要进行一些操作如加法，乘法时，你需要确保操作数的形状是相匹配的，如：你不能将一个具有形状[3, 2]的张量和一个具有[3,4]形状的张量相加。但是，这里有一个特殊情况，那就是当你的其中一个操作数是一个具有单独维度(singular dimension)的张量的时候，TF会隐式地在它的单独维度方向填满(tile)，以确保和另一个操作数的形状相匹配。所以，对一个[3,2]的张量和一个[3,1]的张量相加在TF中是合法的。（译者：这个机制继承自numpy的广播功能。其中所谓的单独维度就是一个维度为1，或者那个维度缺失，具体可参考numpy broadcast）。

import tensorflow as tf

a = tf.constant([[1., 2.], [3., 4.]]) b = tf.constant([[1.], [2.]]) # c = a + tf.tile(b, [1, 2]) c = a + b

• 1
• 2
• 3
• 4
• 5
• 6

广播机制允许我们在隐式情况下进行填充（tile），而这可以使得我们的代码更加简洁，并且更有效率地利用内存，因为我们不需要另外储存填充操作的结果。一个可以表现这个优势的应用场景就是在结合具有不同长度的特征向量的时候。为了拼接具有不同长度的特征向量，我们一般都先填充输入向量，拼接这个结果然后进行之后的一系列非线性操作等。这是一大类神经网络架构的共同套路(common pattern)

a = tf.random_uniform([5, 3, 5])
b = tf.random_uniform([5, 1, 6]) # concat a and b and apply nonlinearity tiled_b = tf.tile(b, [1, 3, 1]) c = tf.concat([a, tiled_b], 2) d = tf.layers.dense(c, 10, activation=tf.nn.relu)

• 1
• 2
• 3
• 4
• 5
• 6
• 7

但是这个可以通过广播机制更有效地完成。我们利用事实f(m(x+y))=f(mx+my)f(m(x+y))=f(mx+my)，简化我们的填充操作。因此，我们可以分离地进行这个线性操作，利用广播机制隐式地完成拼接操作。

pa = tf.layers.dense(a, 10, activation=None)
pb = tf.layers.dense(b, 10, activation=None)
d = tf.nn.relu(pa + pb)

• 1
• 2
• 3

事实上，这个代码足够通用，并且可以在具有抽象形状(arbitrary shape)的张量间应用：

def merge(a, b, units, activation=tf.nn.relu):
    pa = tf.layers.dense(a, units, activation=None) pb = tf.layers.dense(b, units, activation=None) c = pa + pb if activation is not None: c = activation(c) return c

• 1
• 2
• 3
• 4
• 5
• 6
• 7

一个更为通用函数形式如上所述：

目前为止，我们讨论了广播机制的优点，但是同样的广播机制也有其缺点，隐式假设几乎总是使得调试变得更加困难，考虑下面的例子：

a = tf.constant([[1.], [2.]])
b = tf.constant([1., 2.])
c = tf.reduce_sum(a + b)

• 1
• 2
• 3

你猜这个结果是多少？如果你说是6，那么你就错了，答案应该是12.这是因为当两个张量的阶数不匹配的时候，在进行元素间操作之前，TF将会自动地在更低阶数的张量的第一个维度开始扩展，所以这个加法的结果将会变为[[2, 3], [3, 4]]，所以这个reduce的结果是12. 
（译者：答案详解如下，第一个张量的shape为[2, 1]，第二个张量的shape为[2,]。因为从较低阶数张量的第一个维度开始扩展，所以应该将第二个张量扩展为shape=[2,2]，也就是值为[[1,2], [1,2]]。第一个张量将会变成shape=[2,2]，其值为[[1, 1], [2, 2]]。） 
解决这种麻烦的方法就是尽可能地显示使用。我们在需要reduce某些张量的时候，显式地指定维度，然后寻找这个bug就会变得简单：

a = tf.constant([[1.], [2.]])
b = tf.constant([1., 2.])
c = tf.reduce_sum(a + b, 0)

• 1
• 2
• 3

这样，c的值就是[5, 7]，我们就容易猜到其出错的原因。一个更通用的法则就是总是在reduce操作和在使用tf.squeeze中指定维度。

numpi 与 tensorflow 2.4 上的卷积

虽然我认为这个问题大部分是 this question 的重复，但我可以用这个问题来想出一个等效的脚本。

import tensorflow as tf
import numpy as np

I = [3,4,5]
K = [2,1,0]

I = [0] + I + [0]

i = tf.constant(I,dtype=tf.float32,name='i')
k = tf.constant(K,name='k')

data   = tf.reshape(i,[1,int(i.shape[0]),1],name='data')
kernel = tf.reshape(k,[int(k.shape[0]),name='kernel')

res = tf.squeeze(tf.nn.conv1d(data,kernel[::-1],'SAME'))
print(res)
print(np.convolve(I,K,'SAME'))

tf.Tensor([ 6. 11. 14. 5. 0.],shape=(5,),dtype=float32)

[ 6 11 14 5 0]

在您的情况下，他们的关键是了解 tensorflow 和 numpy 如何处理填充。尽管链接的问题很好地解释了这一点，但我还要注意到一个事实，即 full 的默认 np.convolve 填充在 tensorflow conv 1d 中没有等效项。

NumPy arrays and TensorFlow Tensors的区别和联系

1，tensor的特点

• Tensors can be backed by accelerator memory (like GPU, TPU).
• Tensors are immutable

2，双向转换

• TensorFlow operations automatically convert NumPy ndarrays to Tensors.
• NumPy operations automatically convert Tensors to NumPy ndarrays

3，转换的代价

Tensors can be explicitly converted to NumPy ndarrays by invoking the .numpy() method on them. These conversions are typically cheap as the array and Tensor share the underlying memory representation if possible. However, sharing the underlying representation isn''t always possible since the Tensor may be hosted in GPU memory while NumPy arrays are always backed by host memory, and the conversion will thus involve a copy from GPU to host memory.

4，使用tensor时如何测定和选择gpu

x = tf.random_uniform([3, 3])

print("Is there a GPU available: "),
print(tf.test.is_gpu_available())

print("Is the Tensor on GPU #0: "),
print(x.device.endswith(''GPU:0''))

print(tf.test.is_built_with_cuda())

5，显式指定运行的xpu

import time

def time_matmul(x):
start = time.time()
for loop in range(10):
tf.matmul(x, x)

result = time.time()-start

print("10 loops: {:0.2f}ms".format(1000*result))

# Force execution on CPU
print("On CPU:")
with tf.device("CPU:0"):
x = tf.random_uniform([900, 900])
assert x.device.endswith("CPU:0")
time_matmul(x)

# Force execution on GPU #0 if available
if tf.test.is_gpu_available():
with tf.device("GPU:0"): # Or GPU:1 for the 2nd GPU, GPU:2 for the 3rd etc.
x = tf.random_uniform([1000, 1000])
assert x.device.endswith("GPU:0")
time_matmul(x)

numpy 和 tensorflow 中的各种乘法（点乘和矩阵乘）

点乘和矩阵乘的区别：

1）点乘（即“ * ”） ---- 各个矩阵对应元素做乘法

若 w 为 m*1 的矩阵，x 为 m*n 的矩阵，那么通过点乘结果就会得到一个 m*n 的矩阵。

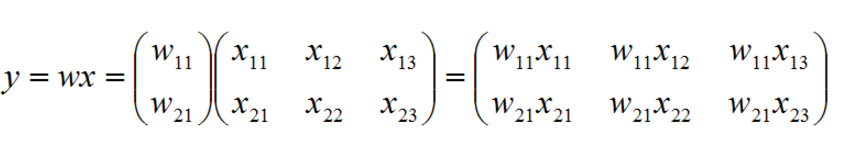
若 w 为 m*n 的矩阵，x 为 m*n 的矩阵，那么通过点乘结果就会得到一个 m*n 的矩阵。

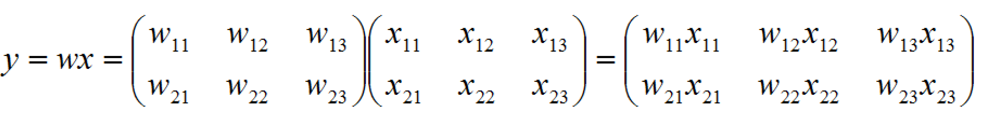
w的列数只能为 1 或 与x的列数相等（即n），w的行数与x的行数相等 才能进行乘法运算。

2）矩阵乘 ---- 按照矩阵乘法规则做运算

若 w 为 m*p 的矩阵，x 为 p*n 的矩阵，那么通过矩阵相乘结果就会得到一个 m*n 的矩阵。

只有 w 的列数 == x的行数 时，才能进行乘法运算

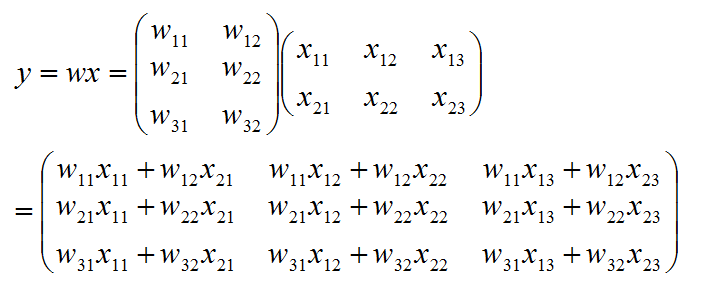
1. numpy

1）点乘

1 import numpy as np
2 
3 w = np.array([[0.4], [1.2]])
4 x = np.array([range(1,6), range(5,10)])
5 
6 print w
7 print x
8 print w*x

运行结果如下图：

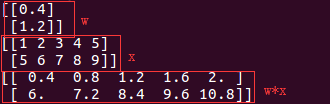
2）矩阵乘

1 import numpy as np
2 
3 w = np.array([[0.4, 1.2]])
4 x = np.array([range(1,6), range(5,10)])
5 
6 print w
7 print x
8 print np.dot(w,x)

运行结果如下：

2. tensorflow

1）点乘

 1 import tensorflow as tf
 2 
 3 w = tf.Variable([[0.4], [1.2]], dtype=tf.float32) # w.shape: [2, 1]
 4 x = tf.Variable([range(1,6), range(5,10)], dtype=tf.float32) # x.shape: [2, 5]
 5 y = w * x     # 等同于 y = tf.multiply(w, x)   y.shape: [2, 5]
 6 
 7 sess = tf.Session()
 8 init = tf.global_variables_initializer()
 9 sess.run(init)
10 
11 print sess.run(w)
12 print sess.run(x)
13 print sess.run(y)

运行结果如下：

2）矩阵乘

 1 # coding:utf-8
 2 import tensorflow as tf
 3 
 4 w = tf.Variable([[0.4, 1.2]], dtype=tf.float32) # w.shape: [1, 2]
 5 x = tf.Variable([range(1,6), range(5,10)], dtype=tf.float32) # x.shape: [2, 5]
 6 y = tf.matmul(w, x) # y.shape: [1, 5]
 7 
 8 sess = tf.Session()
 9 init = tf.global_variables_initializer()
10 sess.run(init)
11 
12 print sess.run(w)
13 print sess.run(x)
14 print sess.run(y)

运行结果如下：

我们今天的关于Tensorflow中的numpy随机选择和tensorflow随机数的分享就到这里，谢谢您的阅读，如果想了解更多关于Effective TensorFlow Chapter 4: TensorFlow中的广播Broadcast机制【转】、numpi 与 tensorflow 2.4 上的卷积、NumPy arrays and TensorFlow Tensors的区别和联系、numpy 和 tensorflow 中的各种乘法（点乘和矩阵乘）的相关信息，可以在本站进行搜索。

本文标签：

• Tensorflow
• numpy
• 随机选择
• tensorflow随机数