以上就是给各位分享使用批处理计算BCE反向传播中的dx,其中也会对bp算法反向传播进行解释,同时本文还将给你拓展caffe中的前向传播和反向传播、Java中的神经网络无法反向传播、Keras模型中的反
以上就是给各位分享使用批处理计算 BCE 反向传播中的 dx,其中也会对bp算法反向传播进行解释,同时本文还将给你拓展caffe 中的前向传播和反向传播、Java 中的神经网络无法反向传播、Keras 模型中的反向传播不会影响所有层?、Python实现深度学习系列之【正向传播和反向传播】等相关知识,如果能碰巧解决你现在面临的问题,别忘了关注本站,现在开始吧!
本文目录一览:- 使用批处理计算 BCE 反向传播中的 dx(bp算法反向传播)
- caffe 中的前向传播和反向传播
- Java 中的神经网络无法反向传播
- Keras 模型中的反向传播不会影响所有层?
- Python实现深度学习系列之【正向传播和反向传播】

使用批处理计算 BCE 反向传播中的 dx(bp算法反向传播)
如何解决使用批处理计算 BCE 反向传播中的 dx?
我正在尝试使用批处理从头开始反向传播,但在计算 dx 时遇到问题。首先,我想先定义变量以避免混淆:
a - The activation value calculated by passing z through an activation function
z - The value before the activation function of the layer
x - The inputs into the layer
w - The weights that connect the inputs to the output nodes
da - The derivative of a
dz - The derivative of z
dx - The derivative of x
我知道这是 x 的导数:
dx = w.T*dz
Note: * means dot and .T means transpose
现在让我介绍一下这个问题。假设我有一个具有 2 个输入、3 个输出节点和 5 个批次大小的神经网络。我将如何计算 dx?在这种情况下,权重在转置之前的形状为 (z,x) 或 (3,2),而 dz 的形状为 (z,batches) 或 (3,5)。如果我使用上面的公式,我会得到 (x,batches) 或 (2,5) 的形状。在使用上面的公式得到 dx(导致形状为 (2,1))之后,我会取最后一个维度的总和吗?下面是使用虚构值的点积表示:
w.T * dz = dx
[[1,2,3,4,5],[[1,0.5,1],* [1,= [[2.5,5,7.5,10,12.5],[-1,-1,-0.5] [1,5]] [-2.5,-5,-7.5,-10,-12.5]]
解决方法
你做的一切都是正确的。在反向传播中,X 始终需要与 dX 具有相同的维度。如果 X 是形状 (2,5) 的中间结果,则梯度也具有形状 (2,5)。通过这种方式,您可以更新矩阵 X。现在在您的情况下,矩阵 X 是输入矩阵,您将永远不会更新它。您只需要更新 W。
如果 X 是隐藏层的结果,则您对反向传播梯度的计算是正确的。

caffe 中的前向传播和反向传播
caffe 中的网络结构是一层连着一层的,在相邻的两层中,可以认为前一层的输出就是后一层的输入,可以等效成如下的模型

可以认为输出 top 中的每个元素都是输出 bottom 中所有元素的函数。如果两个神经元之间没有连接,可以认为相应的权重为0。其实上图的模型只适用于全连接层,其他的如卷积层、池化层,x 与 y 之间很多是没有连接的,可以认为很多权重都是0,而池化层中有可能部分 x 与 y 之间是相等的,可以认为权重是1。
下面用以上的模型来说明反向传播的过程。在下图中,我用虚线将 y 与损失 Loss 之间连接了起来,表示 Loss 必然是由某种函数关系由 y 映射而成,我们只需要知道这个函数是由后面的网络参数决定的,与这一层的网络参数无关就行了。

当我们知道了 Loss 对本层输出的导数 dy,便能推出 Loss 对本层输入 x 及本层网络参数 w 的导数。
先推 Loss 对输入 x 的导数。由
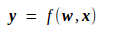
可知,y 对 x 的导数如下,其中 g 为某种函数映射,它由上面的 f 唯一地确定,因而是一种已知的映射。
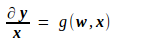
由此推出 Loss 对 x 的导数如下,其中 h 也为某种函数映射,也是由上面的 f 唯一地确定,是一种已知的映射。
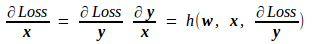
至于 Loss 对该层网络参数 w 的导数,由上述公式很容易得到

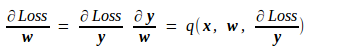
其中的 p、q 和 g、h 一样,都是由 f 确定的已知映射。
从上面的分析中可以看出,只要知道了 Loss 对本层输出的导数 dy,就能计算出本层参数的梯度,并且求出 Loss 对本层输入 x 的导数 dx。反向传播是从最后一层(损失层)向第一层(输出层)传播,损失层中 Loss 对输出的导数 dy 是能直接求取的,并且本层的输入恰是上一层的输出,因此这种计算可以由后向前地递推下去,这就是反向传播的大体过程。最后示意图如下图所示
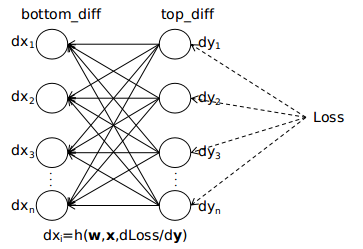
以上便是 caffe 实现反向传播的整体思路。对不同的层,由于前向传播的过程 f 不一样,所以对应的反向传播的过程 p、q 也是不一样的。在后面的章节中,我将结合源代码,分析 ConvolutionLayer、PoolingLayer、InnerProductLayer、ReLULayer、SoftmaxLayer、SoftmaxWithLossLayer 这几种层前向传播、后向传播的具体过程。

Java 中的神经网络无法反向传播
这个问题所涉及的数学量加上缺乏数据/代码复制,几乎不可能回答“我的 NaN 在哪里”的原始问题。
相反,我建议您将这个问题重新考虑为一个更简单的问题,“我如何知道像 NaN 这样的值在我的代码中来自哪里”。
如果您可以在 IDE 中运行您的代码,它们中的大多数将支持条件断点。即,只要变量达到某个值就会暂停代码的断点。在您的情况下,我建议您在首选 IDE 中运行您的代码,并使用条件断点检测值是否为 NaN。
您可以在这篇 SO post 中阅读更多关于如何设置它的信息,其中 NaN 双重检查的主题在此线程中很好地提到: Eclipse Debugger doesn't stop at conditional breakpoint
另一个后续考虑是考虑您需要将这些断点放在哪里。简短的回答是将它们放在计算双精度值的任何地方,因为这些计算中的任何一个都可能引入 NaN。
为此,我提出以下两个建议:
首先,在您当前计算双精度数的位置放置一个断点,以查看 NaN 是否来自这些计算。那将是这两个变量:
double z = ...
double sum = ...
其次,重构您对 gradientOfWeight 的调用以返回到一个临时变量,然后在这些临时计算上放置一个类似的断点。
所以代替
this.weightGradients.get(l)[i][j] = this.gradientOfWeight(l,i,j,target);
你会:
double interrimComputationToListenForNaNon = this.gradientOfWeight(l,target);
this.weightGradients.get(l)[i][j] = interrimComputationToListenForNaNon;
拥有这些中间变量更方便,可以为您提供一种简单的方法来监视计算,而无需以任何显着的方式更改调用。可能有一种更聪明的方法来做到这一点,而无需中间变量,但这种方法似乎最容易监控和解释。
,您看到的 NaN 是由于下溢,您需要使用 BigDecimal 类而不是 double 以获得更高的精度。请参阅这些以更好地理解 bigdecimal class java sample use,BigDecimal API Reference

Keras 模型中的反向传播不会影响所有层?
如何解决Keras 模型中的反向传播不会影响所有层??
我有以下型号
inputs = Input(shape=(8)) # 8 groessen als eingabe
x = Reshape((8,1))(inputs)
# generator
x = Bidirectional(LSTM(32,return_sequences=True))(x)
x = Bidirectional(LSTM(64,return_sequences=True))(x)
generated = LSTM(4,return_sequences=True,activation="sigmoid")(x)
# rating
x = Bidirectional(LSTM(128,return_sequences=True))(generated)
x = Bidirectional(LSTM(128))(x)
x = Flatten()(x)
x = Dense(16,activation="relu")(x)
rating = Dense(8,activation="relu")(x)
model = Model(inputs=inputs,outputs=[rating,generated])
return model
我向模型输入一个序列 (8,),生成器应该从这个序列中创建一个满足某些条件的新序列 (8,4)。有很多输出可以满足这个条件,但我的生成器应该只取一个它喜欢的。
然后我将生成的序列提供给下一层,在那里我计算此输出的值 (8,) 以便能够在应用我的损失函数时获得梯度
rating,generated = model(model_input,training=True)
calculated_rating = my_numeric_function(np.array(generated))
loss_1 = mse(model_input,rating) # the rating-loss
loss_2 = mse(calculated_rating,rating) # the loss between rating and generator
metric = mse(model_input,calculated_rating) # metric: difference between model input and real calculated
tape.gradient(loss_1+loss_2,model.trainable_weights)
我的 loss1 和 loss2 正在减少,但指标(calculated_rating - 生成)保持完全相同。
似乎在反向传播中,我的损失函数不允许更改生成器层的权重。
指标没有减少的原因可能是什么? (它保持在 51-52 左右)
解决方法
暂无找到可以解决该程序问题的有效方法,小编努力寻找整理中!
如果你已经找到好的解决方法,欢迎将解决方案带上本链接一起发送给小编。
小编邮箱:dio#foxmail.com (将#修改为@)

Python实现深度学习系列之【正向传播和反向传播】
前言
在了解深度学习框架之前,我们需要自己去理解甚至去实现一个网络学习和调参的过程,进而理解深度学习的机理;
为此,博主这里提供了一个自己编写的一个例子,带领大家理解一下网络学习的正向传播和反向传播的过程;
除此之外,为了实现batch读取,我还设计并提供了一个简单的DataLoader类去模拟深度学习中数据迭代器的取样;并且提供了存取模型的函数;
值得注意的是仅仅使用python实现,因此对于环境的需求不是很大,希望各位可以多多star我的博客和github,学习到更有用的知识!!

目录
一、实现效果
二、整体代码框架
三、详细代码说明
1.数据处理
2.网络设计
3.激活函数
4.训练
四、训练演示
五、总结
一、实现效果
实现一个由多个Linear层构成的网络来拟合函数,项目地址:https://github.com/nickhuang1996/HJLNet,运行:
python demo.py
拟合函数为: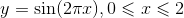
以下结果从左到右依次为(学习率为0.03,batchsize为90):
Epoch:400,1000, 2000, 10000以上
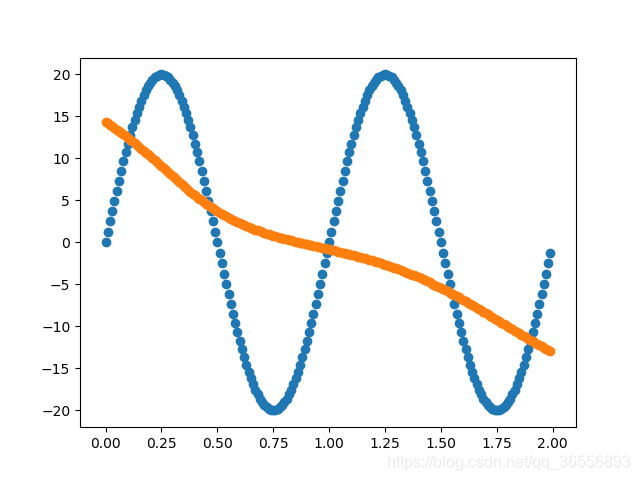
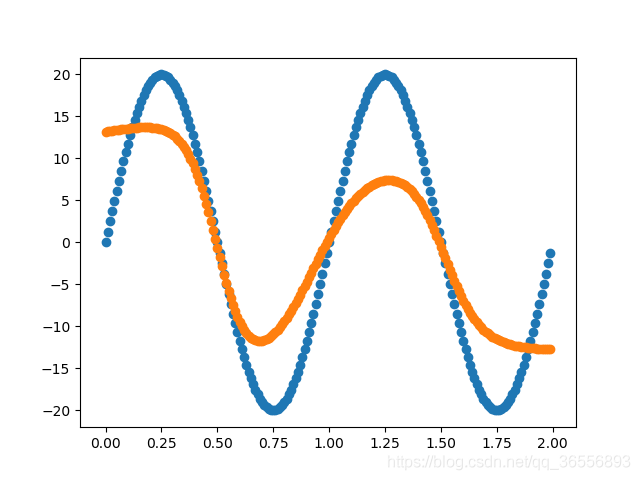
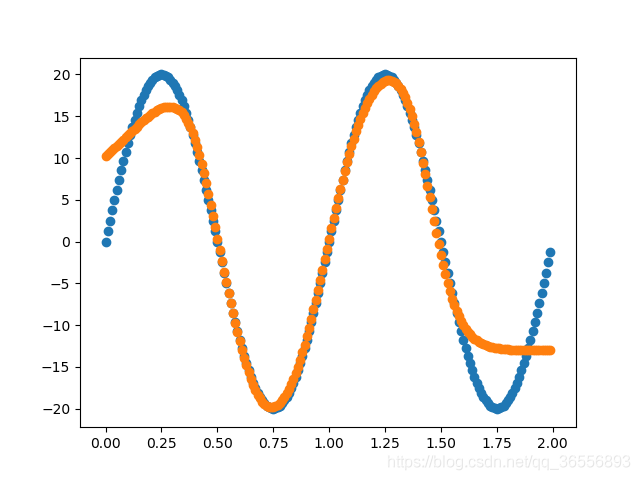
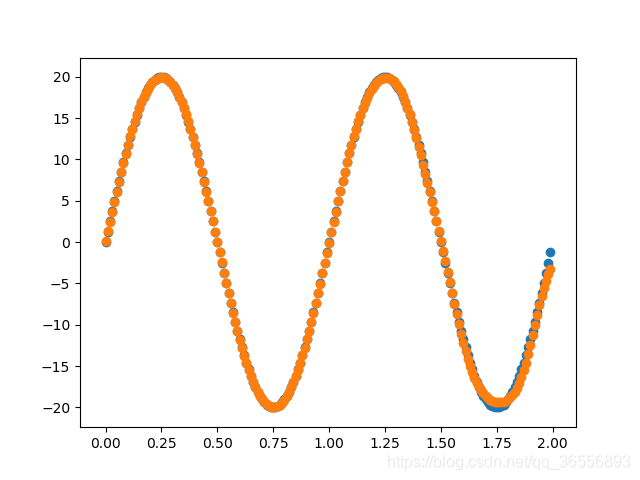
二、整体代码框架

三、详细代码说明
1.数据处理
Dataset.py
x是0到2之间的数据,步长为0.01,因此是200个数据;
y是目标函数,振幅为20;
length是数据长度;
_build_items()是建立一个dict存储x和y;
_transform()是对x和y进行数据的变换;
import numpy as np
class Dataset:
def __init__(self):
self.x = np.arange(0.0, 2.0, 0.01)
self.y = 20 * np.sin(2 * np.pi * self.x)
self.length = len(list(self.x))
self._build_items()
self._transform()
def _build_items(self):
self.items = [{
''x'': list(self.x)[i],
''y'': list(self.y)[i]
}for i in range(self.length)]
def _transform(self):
self.x = self.x.reshape(1, self.__len__())
self.y = self.y.reshape(1, self.__len__())
def __len__(self):
return self.length
def __getitem__(self, index):
return self.items[index]DataLoader.py
类似于Pytorch里的DataLoader,博主这里初始化也传入两个参数:dataset和batch_size
__next__()就是每次迭代执行的函数,利用__len__()得到dataset的长度,利用__getitem__()得到数据集里的数据;
_concate()就是把一个batch的数据拼接起来;
_transform()就是转换一个batch的数据形式;
import numpy as np
class DataLoader:
def __init__(self, dataset, batch_size):
self.dataset = dataset
self.batch_size = batch_size
self.current = 0
def __next__(self):
if self.current < self.dataset.__len__():
if self.current + self.batch_size <= self.dataset.__len__():
item = self._concate([self.dataset.__getitem__(index) for index in range(self.current, self.current + self.batch_size)])
self.current += self.batch_size
else:
item = self._concate([self.dataset.__getitem__(index) for index in range(self.current, self.dataset.__len__())])
self.current = self.dataset.__len__()
return item
else:
self.current = 0
raise StopIteration
def _concate(self, dataset_items):
concated_item = {}
for item in dataset_items:
for k, v in item.items():
if k not in concated_item:
concated_item[k] = [v]
else:
concated_item[k].append(v)
concated_item = self._transform(concated_item)
return concated_item
def _transform(self, concated_item):
for k, v in concated_item.items():
concated_item[k] = np.array(v).reshape(1, len(v))
return concated_item
def __iter__(self):
return self
2.网络设计
Linear.py
类似于Pytorch里的Linear,博主这里初始化也传入三个参数:in_features, out_features, bias
_init_parameters()是初始化权重weight和偏置bias,weight大小是[out_features, in_features],bias大小是[out_features, 1]
forward就是前向传播: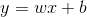
import numpy as np
class Linear:
def __init__(self, in_features, out_features, bias=False):
self.in_features = in_features
self.out_features = out_features
self.bias = bias
self._init_parameters()
def _init_parameters(self):
self.weight = np.random.random([self.out_features, self.in_features])
if self.bias:
self.bias = np.zeros([self.out_features, 1])
else:
self.bias = None
def forward(self, input):
return self.weight.dot(input) + self.bias
*network.py
一个简单的多层Linear网络
_init_parameters()是把Linear层里的权重和偏执都放在一个dict里存储;
forward()就是前向传播,最后一层不经过Sigmoid;
backward()就是反向传播,利用梯度下降实现误差传递和调参:例如一个两层的Linear层的反向传播如下
![dz^{[1]}=a^{[1]}-y}](https://oscimg.oschina.net/oscnet/up-1897ba2686437329dc51d16280333f79.gif)
![dW^{[1]}=dz^{[1]}a^{[1]}^{T}}](https://oscimg.oschina.net/oscnet/up-b4feecc1e0b00a6ceee1642e189aaa91.gif)
![db^{[1]}=dz^{[1]}](https://oscimg.oschina.net/oscnet/up-389a46b05441d14c9f4919b6ca0b1b89.gif)
![dz^{[0]}=W^{[1]}^{T}dz^{[1]}\ast S^{[0]}''(z^{[0]}) }](https://oscimg.oschina.net/oscnet/up-b693b67575828fe67ec17294a522ba95.gif)
![dW^{[0]}=dz^{[0]}x^{T}}](https://oscimg.oschina.net/oscnet/up-ccfd70526305070fa5fc53b1a65f84f5.gif)
![db^{[0]}=dz^{[0]}](https://oscimg.oschina.net/oscnet/up-31b9447684a6c51946ccd4b8287f5d61.gif)
update_grads()是更新权重和偏置;
# -*- coding: UTF-8 -*-
import numpy as np
from ..lib.Activation.Sigmoid import sigmoid_derivative, sigmoid
from ..lib.Module.Linear import Linear
class network:
def __init__(self, layers_dim):
self.layers_dim = layers_dim
self.linear_list = [Linear(layers_dim[i - 1], layers_dim[i], bias=True) for i in range(1, len(layers_dim))]
self.parameters = {}
self._init_parameters()
def _init_parameters(self):
for i in range(len(self.layers_dim) - 1):
self.parameters["w" + str(i)] = self.linear_list[i].weight
self.parameters["b" + str(i)] = self.linear_list[i].bias
def forward(self, x):
a = []
z = []
caches = {}
a.append(x)
z.append(x)
layers = len(self.parameters) // 2
for i in range(layers):
z_temp = self.linear_list[i].forward(a[i])
self.parameters["w" + str(i)] = self.linear_list[i].weight
self.parameters["b" + str(i)] = self.linear_list[i].bias
z.append(z_temp)
if i == layers - 1:
a.append(z_temp)
else:
a.append(sigmoid(z_temp))
caches["z"] = z
caches["a"] = a
return caches, a[layers]
def backward(self, caches, output, y):
layers = len(self.parameters) // 2
grads = {}
m = y.shape[1]
for i in reversed(range(layers)):
# 假设最后一层不经历激活函数
# 就是按照上面的图片中的公式写的
if i == layers - 1:
grads["dz" + str(i)] = output - y
else: # 前面全部都是sigmoid激活
grads["dz" + str(i)] = self.parameters["w" + str(i + 1)].T.dot(
grads["dz" + str(i + 1)]) * sigmoid_derivative(
caches["z"][i + 1])
grads["dw" + str(i)] = grads["dz" + str(i)].dot(caches["a"][i].T) / m
grads["db" + str(i)] = np.sum(grads["dz" + str(i)], axis=1, keepdims=True) / m
return grads
# 就是把其所有的权重以及偏执都更新一下
def update_grads(self, grads, learning_rate):
layers = len(self.parameters) // 2
for i in range(layers):
self.parameters["w" + str(i)] -= learning_rate * grads["dw" + str(i)]
self.parameters["b" + str(i)] -= learning_rate * grads["db" + str(i)]3.激活函数
Sigmoid.py
公式定义: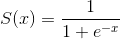
导数可由自身表示: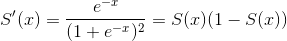
import numpy as np
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
def sigmoid_derivative(x):
return sigmoid(x) * (1 - sigmoid(x))
4.训练
demo.py
训练模型的入口文件,包含训练、测试和存储模型
from code.scripts.trainer import Trainer
from code.config.default_config import _C
if __name__ == ''__main__'':
trainer = Trainer(cfg=_C)
trainer.train()
trainer.test()
trainer.save_models()
default_config.py
配置文件:
layers_dim代表Linear层的输入输出维度;
batch_size是batch的大小;
total_epochs是总体的训练时间,训练一次x为一个epoch;
resume是判断继续训练;
result_img_path是结果存储的路径;
ckpt_path是模型存储的路径;
from easydict import EasyDict
_C = EasyDict()
_C.layers_dim = [1, 25, 1] # [1, 30, 10, 1]
_C.batch_size = 90
_C.total_epochs = 40000
_C.resume = True # False means retraining
_C.result_img_path = "D:/project/Pycharm/HJLNet/result.png"
_C.ckpt_path = ''D:/project/Pycharm/HJLNet/ckpt.npy''trainer.py
这里不多赘述,主要利用train()这个函数进行训练,test()进行测试
from ..lib.Data.DataLoader import DataLoader
from ..scripts.Dataset import Dataset
from ..scripts.network import network
import matplotlib.pyplot as plt
import numpy as np
class Trainer:
def __init__(self, cfg):
self.ckpt_path = cfg.ckpt_path
self.result_img_path = cfg.result_img_path
self.layers_dim = cfg.layers_dim
self.net = network(self.layers_dim)
if cfg.resume:
self.load_models()
self.dataset = Dataset()
self.dataloader = DataLoader(dataset=self.dataset, batch_size=cfg.batch_size)
self.total_epochs = cfg.total_epochs
self.iterations = 0
self.x = self.dataset.x
self.y = self.dataset.y
self.draw_data(self.x, self.y)
def train(self):
for i in range(self.total_epochs):
for item in self.dataloader:
caches, output = self.net.forward(item[''x''])
grads = self.net.backward(caches, output, item[''y''])
self.net.update_grads(grads, learning_rate=0.03)
if i % 100 == 0:
print("Epoch: {}/{} Iteration: {} Loss: {}".format(i + 1,
self.total_epochs,
self.iterations,
self.compute_loss(output, item[''y''])))
self.iterations += 1
def test(self):
caches, output = self.net.forward(self.x)
self.draw_data(self.x, output)
self.save_results()
self.show()
def save_models(self):
ckpt = {
"layers_dim": self.net.layers_dim,
"parameters": self.net.linear_list
}
np.save(self.ckpt_path, ckpt)
print(''Save models finish!!'')
def load_models(self):
ckpt = np.load(self.ckpt_path).item()
self.net.layers_dim = ckpt["layers_dim"]
self.net.linear_list = ckpt["parameters"]
print(''load models finish!!'')
def draw_data(self, x, y):
plt.scatter(x, y)
def show(self):
plt.show()
def save_results(self):
plt.savefig(fname=self.result_img_path, figsize=[10, 10])
# 计算误差值
def compute_loss(self, output, y):
return np.mean(np.square(output - y))
四、训练演示
训练期间会输出训练的时间,迭代次数和损失变化,训练结束存储模型和结果。
1.开始训练
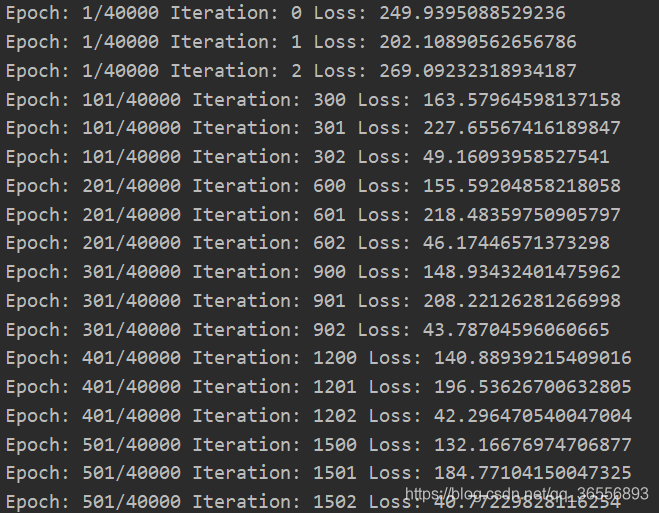
2.训练完毕,读取上次的模型继续训练
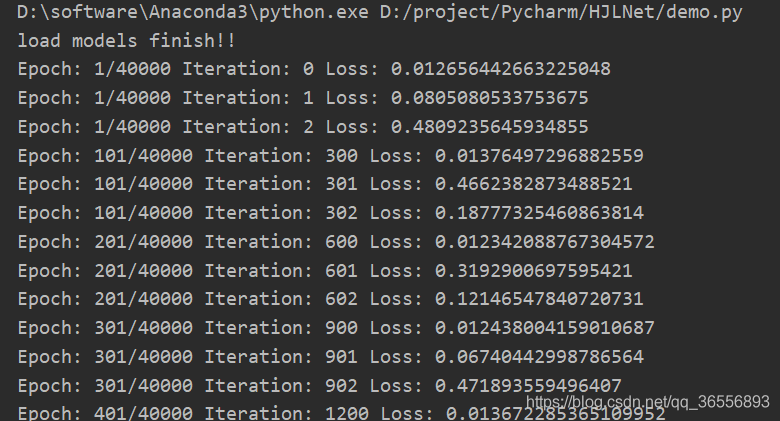
3.结果展示
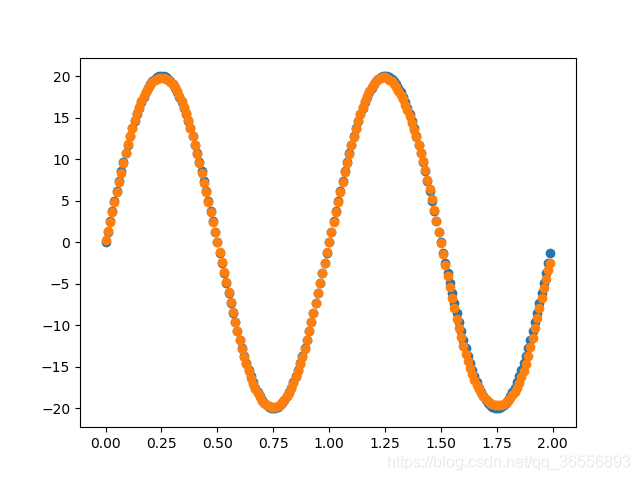
五、总结
如此一来便知晓了一个基本网络训练过程中正向反向传播过程,之后会更新更加详细的代码和原理,帮助各位学习深度学习的知识和概念~
本文分享 CSDN - 悲恋花丶无心之人。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。
今天关于使用批处理计算 BCE 反向传播中的 dx和bp算法反向传播的介绍到此结束,谢谢您的阅读,有关caffe 中的前向传播和反向传播、Java 中的神经网络无法反向传播、Keras 模型中的反向传播不会影响所有层?、Python实现深度学习系列之【正向传播和反向传播】等更多相关知识的信息可以在本站进行查询。
本文标签:





