GVKun编程网logo

计算极坐标中样条曲线的梯度（极坐标 梯度）

22

对于想了解计算极坐标中样条曲线的梯度的读者，本文将是一篇不可错过的文章，我们将详细介绍极坐标梯度，并且为您提供关于AndroidLineChart绘制多条曲线的方法、BsplineCatmullRoo

对于想了解计算极坐标中样条曲线的梯度的读者，本文将是一篇不可错过的文章，我们将详细介绍极坐标 梯度，并且为您提供关于Android LineChart绘制多条曲线的方法、Bspline CatmullRoom and Bezier 样条曲线生成、B样条曲线上的最近点？、B样条曲线方程和C++实现的有价值信息。

本文目录一览：

计算极坐标中样条曲线的梯度（极坐标 梯度）

计算极坐标中样条曲线的梯度（极坐标 梯度）

如何解决计算极坐标中样条曲线的梯度？

我想计算样条曲线的梯度，并在极坐标图中将其可视化。

我用tck,u = splprep()获得具有直角坐标的样条，而splev(u,tck,der=1)分别计算其在x和y方向上的偏导数。然后，我计算出应该用于可视化渐变的箭头的端点，并将其转换为极坐标。

乍一看，该图看起来不错，但是，如果我将梯度的估计方向与解析解进行比较，即使增加点数也存在显着差异。

MWE 

from matplotlib import pyplot as plt
import numpy as np
from scipy.interpolate import splprep,splev

if __name__ == ''__main__'':
    N = 11  # number of samples
    # x = np.arange(0,N)  # [Update] This did not decrease the step size for increasing N
    x = np.linspace(0,10,N)
    y = np.sin(x)

    tck,u = splprep([x,y],s=0)  # spline

    theta,r = np.arctan2(y,x),np.hypot(x,y)  # convert to polar

    gradient = splev(u,der=1) # compute first derivative

    # normalize
    gradient = gradient / np.hypot(gradient[0],gradient[1])

    # compare numerical and analytical solution
    # direction = np.arctan2(gradient[1],gradient[0])  # [Update] this was wrong
    slope = gradient[1] / gradient[0]
    print(np.cos(x) - slope)  # cos(x) should be the analytical solution

    endpoints_x = x + gradient[0]
    endpoints_y = y + gradient[1]

    # convert cartesian endpoints to polar
    endpoints_theta,endpoints_r = np.arctan2(endpoints_y,endpoints_x),\
                                   np.hypot(endpoints_x,endpoints_y)


    fig,ax = plt.subplots(1,1,subplot_kw=dict(polar=True))

    plt.scatter(theta,r,marker=''o'')

    plt.plot(np.stack((theta,endpoints_theta)),np.stack((r,endpoints_r)),''r'')

    plt.show()

屏幕截图

Gradient of a spline in polar coordinates

更新

我发现了两个错误。首先，当我使用x时，N中的步长并没有通过增加np.arange(0,N)而减小。其次，我期望数值解为arctan2(gradient[1],gradient[0])，但它只是笛卡尔坐标中的斜率gradient[1] / gradient[0]。

现在一切正常。

解决方法

暂无找到可以解决该程序问题的有效方法，小编努力寻找整理中！

如果你已经找到好的解决方法，欢迎将解决方案带上本链接一起发送给小编。

小编邮箱:dio#foxmail.com (将#修改为@）

Android LineChart绘制多条曲线的方法

Android LineChart绘制多条曲线的方法

本文实例为大家分享了Android LineChart绘制多条曲线的具体代码，供大家参考，具体内容如下

目标效果：

1.新建custom_marker_view.xml页面作为点击弹出框的页面：

<?xml version="1.0" encoding="utf-8"?>
<RelativeLayout xmlns:android="http://schemas.android.com/apk/res/android"
 android:layout_width="wrap_content"
 android:layout_height="40dp"
 android:background="@drawable/marker2" >
 
 <TextView
 android:id="@+id/tvContent"
 android:layout_width="wrap_content"
 android:layout_height="wrap_content"
 android:layout_centerHorizontal="true"
 android:layout_marginTop="7dp"
 android:layout_marginLeft="5dp"
 android:layout_marginRight="5dp"
 android:text=""
 android:textSize="12dp"
 android:textColor="@android:color/white"
 android:ellipsize="end"
 android:singleLine="true"
 android:textAppearance="?android:attr/textAppearanceSmall" />
 
</RelativeLayout>

2.activity_main.xml页面：

<RelativeLayout xmlns:android="http://schemas.android.com/apk/res/android"
 xmlns:tools="http://schemas.android.com/tools"
 android:layout_width="match_parent"
 android:layout_height="match_parent"
 android:paddingBottom="10dp"
 android:paddingLeft="10dp"
 android:paddingRight="10dp"
 android:paddingTop="10dp"
 tools:context=".MainActivity" >
 
 <com.github.mikephil.charting.charts.LineChart
 android:id="@+id/chartTall"
 android:layout_width="match_parent"
 android:layout_height="400dp"
 android:layout_marginTop="20dp" />
 
 
</RelativeLayout>

3.新建MyMarkerView.java重写MarkView控件：

package com.example.weixu.drawline;
 
import android.content.Context;
import android.widget.TextView;
 
import com.github.mikephil.charting.data.CandleEntry;
import com.github.mikephil.charting.data.Entry;
import com.github.mikephil.charting.utils.MarkerView;
import com.github.mikephil.charting.utils.Utils;
 
public class MyMarkerView extends MarkerView {
 
 private TextView tvContent;
 
 public MyMarkerView(Context context, int layoutResource) {
 super(context, layoutResource);
 
 tvContent = (TextView) findViewById(R.id.tvContent);
 }
 
 @Override
 public void refreshContent(Entry e, int dataSetIndex) {
 
 if (e instanceof CandleEntry) {
 CandleEntry ce = (CandleEntry) e;
 tvContent.setText("" + Utils.formatNumber(ce.getHigh(), 0, true));
 } else {
 tvContent.setText("" +e.getVal());
 }
 }
}

4.MainActivity.java页面：

package com.example.weixu.drawline;
 
import java.util.ArrayList;
 
import android.app.Activity;
import android.graphics.Color;
import android.graphics.Typeface;
import android.os.Bundle;
import android.view.WindowManager;
 
import com.github.mikephil.charting.charts.BarLineChartBase;
import com.github.mikephil.charting.charts.BarLineChartBase.BorderPosition;
import com.github.mikephil.charting.charts.LineChart;
import com.github.mikephil.charting.data.Entry;
import com.github.mikephil.charting.data.LineData;
import com.github.mikephil.charting.data.LineDataSet;
import com.github.mikephil.charting.utils.Legend;
import com.github.mikephil.charting.utils.Legend.LegendForm;
import com.github.mikephil.charting.utils.XLabels;
import com.github.mikephil.charting.utils.XLabels.XLabelPosition;
import com.github.mikephil.charting.utils.YLabels;
 
public class MainActivity extends Activity {
 
 private LineChart chartTall;
 
 @Override
 protected void onCreate(Bundle savedInstanceState) {
 super.onCreate(savedInstanceState);
 getWindow().setFlags(WindowManager.LayoutParams.FLAG_FULLSCREEN,
 WindowManager.LayoutParams.FLAG_FULLSCREEN);
 setContentView(R.layout.activity_main);
 
 chartTall = (LineChart) findViewById(R.id.chartTall);
 
 setType();
 
 // 刷新图表
 chartTall.invalidate();
 }
 
 private void setType() {
 // 设置在Y轴上是否是从0开始显示
 chartTall.setStartAtZero(true);
 //是否在Y轴显示数据，就是曲线上的数据
 chartTall.setDrawYValues(true);
 //设置网格
 chartTall.setDrawBorder(true);
 chartTall.setBorderPositions(new BarLineChartBase.BorderPosition[] {
 BorderPosition.BOTTOM});
 //在chart上的右下角加描述
 chartTall.setDescription("身高曲线图");
 //设置Y轴上的单位
 chartTall.setUnit("cm");
 //设置透明度
 chartTall.setAlpha(0.8f);
 //设置网格底下的那条线的颜色
 chartTall.setBorderColor(Color.rgb(213, 216, 214));
 //设置Y轴前后倒置
 chartTall.setInvertYAxisEnabled(false);
 //设置高亮显示
 chartTall.setHighlightEnabled(true);
 //设置是否可以触摸，如为false，则不能拖动，缩放等
 chartTall.setTouchEnabled(true);
 //设置是否可以拖拽，缩放
 chartTall.setDragEnabled(true);
 chartTall.setScaleEnabled(true);
 //设置是否能扩大扩小
 chartTall.setPinchZoom(true);
 //设置点击chart图对应的数据弹出标注
 MyMarkerView mv = new MyMarkerView(this, R.layout.custom_marker_view);
 mv.setOffsets(-mv.getMeasuredWidth() / 2, -mv.getMeasuredHeight());
 chartTall.setMarkerView(mv);
 chartTall.setHighlightIndicatorEnabled(false);
 //设置字体格式，如正楷
 Typeface tf = Typeface.createFromAsset(getAssets(),
 "OpenSans-Regular.ttf");
 chartTall.setValueTypeface(tf);
 
 XLabels xl = chartTall.getXLabels();
 xl.setPosition(XLabelPosition.BOTTOM); // 设置X轴的数据在底部显示
 xl.setTypeface(tf); // 设置字体
 xl.setTextSize(10f); // 设置字体大小
 xl.setSpaceBetweenLabels(3); // 设置数据之间的间距
 
 YLabels yl = chartTall.getYLabels();
 yl.setTypeface(tf); // 设置字体
 yl.setTextSize(10f); // s设置字体大小
 yl.setLabelCount(5); // 设置Y轴最多显示的数据个数
 // 加载数据
 setData();
 //从X轴进入的动画
 chartTall.animateX(4000);
 chartTall.animateY(3000); //从Y轴进入的动画
 chartTall.animateXY(3000, 3000); //从XY轴一起进入的动画
 
 //设置最小的缩放
 chartTall.setScaleMinima(0.5f, 1f);
 
 }
 
 private void setData() {
 String[] babAge = {"0","1","2","3","4","5","6"}; //连线的x轴数据
 String[] babyTall = {"50","60","90","110","130","135","140"};
 String[] usuaTall = {"55","65","95","115","125","135","145"};//连线的y轴数据
 
 LineData data=new LineData(babAge,setLine(babAge,babyTall,1,"宝宝身高")); //创建LineData实体类并添加第一条曲线
 data.addDataSet(setLine(babAge,usuaTall,2,"正常身高")); //添加第二条曲线
 chartTall.setData(data);
 }
 
 //画线
 private LineDataSet setLine(String[] babAge, String[] Tall,int flag,String name) {
 ArrayList<String> xValsAge = new ArrayList<String>();
 for (int i = 0; i < babAge.length; i++) {
 xValsAge.add(babAge[i]);
 }
 ArrayList<Entry> yValsBabyTall = new ArrayList<Entry>();
 for (int i = 0; i < Tall.length; i++) {
 yValsBabyTall.add(new Entry(Float.parseFloat(Tall[i]), i));
 }
 //设置baby的成长曲线
 LineDataSet setData = new LineDataSet(yValsBabyTall,name);
 setData.setDrawCubic(true); //设置曲线为圆滑的线
 setData.setCubicIntensity(0.2f);
 setData.setDrawFilled(false); //设置包括的范围区域填充颜色
 setData.setDrawCircles(true); //设置有圆点
 setData.setLineWidth(2f); //设置线的宽度
 setData.setCircleSize(5f); //设置小圆的大小
 setData.setHighLightColor(Color.rgb(244, 117, 117));
 //设置曲线颜色
 if(flag==1)
 setData.setColor(Color.rgb(104, 241, 175)); //宝宝身高曲线颜色
 else if(flag==2)
 setData.setColor(Color.rgb(255, 0, 0)); //普通身高曲线颜色
 return setData; //返回曲线
 }
}

源码：点击打开链接

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持。

您可能感兴趣的文章:
  • Android把商品添加到购物车的动画效果（贝塞尔曲线）
  • Android 曲线图的绘制示例代码
  • Android利用MPAndroidChart绘制曲线图表的基础教程
  • Android编程之canvas绘制各种图形(点,直线,弧,圆,椭圆,文字,矩形,多边形,曲线,圆角矩形)
  • Android实现价格走势自定义曲线图
  • Android 利用三阶贝塞尔曲线绘制运动轨迹的示例
  • android贝塞尔曲线实现波浪效果
  • Android贝塞尔曲线初步学习第二课 仿QQ未读消息气泡拖拽黏连效果
  • Android中贝塞尔曲线的绘制方法示例代码
  • Android实现动态曲线绘制

Bspline CatmullRoom and Bezier 样条曲线生成

Bspline CatmullRoom and Bezier 样条曲线生成

此项目旨在生成常见的样条曲线，项目inspired by 叶飞影

首先是各种曲线的基类

#ifndef __SPLINE_BASE__
#define __SPLINE_BASE__

#include <cstddef>

class SplineBase
{
public:
    // 计算样条数值
    virtual bool BuildSpline(const void* ctrlValuesPtr, int ctrlStride, int ctrlCount, void* splineValuesPtr, int splineStride) const = NULL;

    // 计算切线数值
    virtual bool BuildTangent(const void* ctrlValuesPtr, int ctrlStride, int ctrlCount, void* tangentValuesPtr, int tangentStride) const
    {
        return false;
    }
};

inline float YfGetFloatValue(const void* valuesPtr, int stride, int index)
{
    return *(float*)((char*)valuesPtr + stride * index);
}

#endif //__SPLINE_BASE__

每种曲线的类都会继承此基类，并实现 BuildSpline或者同时实现BuildSpline和Buildtangent两个函数。三种曲线中，三阶及以上阶数的Bezier曲线只通过起始控制点和终点，B样条曲线不会经过其控制点，CatmullRoom曲线会通过所有控制点。BSpline和CatmullRoom样条公式要求4个控制点，然后给出位于第2和第3点之间的光滑曲线(效果如下图，图片来源游戏编程精粹1)。为了得到第1个控制点和第2个控制点之间的点，可以将第一个控制点输入两次，同理第3和第4个控制点之间的曲线需要第四点输入两次。

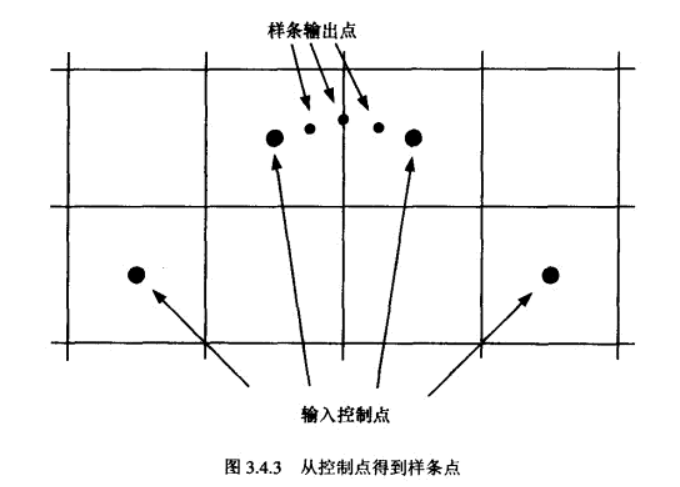
N阶Bezier 曲线

1. 原理参考我的另外一篇博客：N 阶贝塞尔曲线生成，此篇代码每次都要计算N次方，比较耗时，可以在绘制图形之前，先计算好各阶数值即可。如下代码分别是bezier.h 和 bezier.cpp实现N阶贝塞尔曲线

/****************************************************************

  File name   :  bezier.h
  Author      :  Shike
  Version     :  1.0
  Create Date :  2020/05/01
  Description :  Bezier Spline

*****************************************************************/

#ifndef __BEZIER__SPLINE__
#define __BEZIER__SPLINE__

#include "spline_base.h"

#define YD_MAX_BEZIER_CONTROL_VALUE 33

class Bezier : public SplineBase
{
public:
    Bezier();
    ~Bezier();

    // 设置输出样条值的数目
    void SetSplineValuesCount(int count);

    // 获得输出样条值的数目
    int GetSplineValuesCount() const;

    // 计算样条数值
    bool BuildSpline(const void* ctrlValuesPtr, int ctrlStride, int ctrlCount, void* splineValuesPtr, int splineStride) const;

protected:
    void ClearPowT();
    void BuildPowT();
    
    double GetValueT(int t, int p) const
    {
        return m_pow_t[YD_MAX_BEZIER_CONTROL_VALUE*t + p];
    }

protected:
    int    m_valuesCount;
    double *m_pow_t;

protected:
    static void BuildYanghuiTriangle();

    //pascal''s triangle
    static int  m_yanghuiRowIndex[YD_MAX_BEZIER_CONTROL_VALUE];
    static int  m_yanghuiTriangle[(YD_MAX_BEZIER_CONTROL_VALUE + 1)*YD_MAX_BEZIER_CONTROL_VALUE / 2];

};

#endif // __BEZIER__SPLINE__

bezier.cpp

#include "bezier.h"
#include "assert.h"
#include "stdlib.h"

#include <cstdio>

int Bezier::m_yanghuiRowIndex[YD_MAX_BEZIER_CONTROL_VALUE] = { 0 };
int Bezier::m_yanghuiTriangle[(YD_MAX_BEZIER_CONTROL_VALUE + 1)*YD_MAX_BEZIER_CONTROL_VALUE / 2] = { 0 };

Bezier::Bezier()
{
    if (m_yanghuiTriangle[0] == 0)
    {
        BuildYanghuiTriangle();
    }

    m_valuesCount = 0;
    m_pow_t = NULL;

    SetSplineValuesCount(100);
}

Bezier::~Bezier()
{
    ClearPowT();
}

void Bezier::BuildYanghuiTriangle()
{
    // 第0行
    m_yanghuiRowIndex[0] = 0;
    m_yanghuiTriangle[0] = 1;

    int index = 1;
    int t0, t1;
    int* lastRow;

    for (int i = 1; i < YD_MAX_BEZIER_CONTROL_VALUE; i++)
    {
        m_yanghuiRowIndex[i] = index;
        m_yanghuiTriangle[index] = 1;
        index++;

        for (int j = 1; j <= i; j++)
        {
            lastRow = m_yanghuiTriangle + m_yanghuiRowIndex[i - 1];
            t0 = lastRow[j - 1];
            t1 = (j < i) ? lastRow[j] : 0;

            m_yanghuiTriangle[index] = t0 + t1;
            index++;
        }
    }

    assert(index == (YD_MAX_BEZIER_CONTROL_VALUE + 1)*YD_MAX_BEZIER_CONTROL_VALUE / 2);
}

//设置输出样条值的数目
void Bezier::SetSplineValuesCount(int count)
{
    if (count < 2)
    {
        count = 2;
    }

    if (count == m_valuesCount)
    {
        return;
    }

    m_valuesCount = count;
    BuildPowT();
}

//获得输出样条值的数目
int Bezier::GetSplineValuesCount() const
{
    return m_valuesCount;
}

void Bezier::ClearPowT()
{
    if (m_pow_t)
    {
        free(m_pow_t);
        m_pow_t = NULL;
    }
}

void Bezier::BuildPowT()
{
    ClearPowT();

    m_pow_t = (double*)malloc(m_valuesCount*YD_MAX_BEZIER_CONTROL_VALUE * sizeof(double));
    double t;
    for (int i = 0; i < m_valuesCount; i++)
    {
        t = i / (m_valuesCount - 1.0f);

        m_pow_t[i*YD_MAX_BEZIER_CONTROL_VALUE] = 1.0f;
        for (int j = 1; j < YD_MAX_BEZIER_CONTROL_VALUE; j++)
        {
            m_pow_t[i*YD_MAX_BEZIER_CONTROL_VALUE + j] = m_pow_t[i*YD_MAX_BEZIER_CONTROL_VALUE + j - 1] * t;
        }
    }
}

//计算样条数值
bool Bezier::BuildSpline(const void* ctrlValuesPtr, int ctrlStride, int ctrlCount, void* splineValuesPtr, int splineStride) const
{
    if (ctrlCount < 2 || ctrlCount > YD_MAX_BEZIER_CONTROL_VALUE)
    {
        return false;
    }

    double* destValue;
    double* srcValue;
    double v;
    const int* yanghuiRow = m_yanghuiTriangle + m_yanghuiRowIndex[ctrlCount - 1];

    for (int i = 0; i < m_valuesCount; i++)
    {
        for (int dim = 0; dim < ctrlStride; dim++)
        {
            v = 0.0f;
            for (int j = 0; j < ctrlCount; j++)
            {
                srcValue = (double*)ctrlValuesPtr + ctrlStride * j + dim;
                v += yanghuiRow[j] * (*srcValue) * GetValueT(i, j) * GetValueT(m_valuesCount - 1 - i, ctrlCount - 1 - j);
            }

            destValue = (double*)splineValuesPtr + splineStride * i + dim;
            *destValue = v;
        }
    }

    return true;
}

显示效果如下

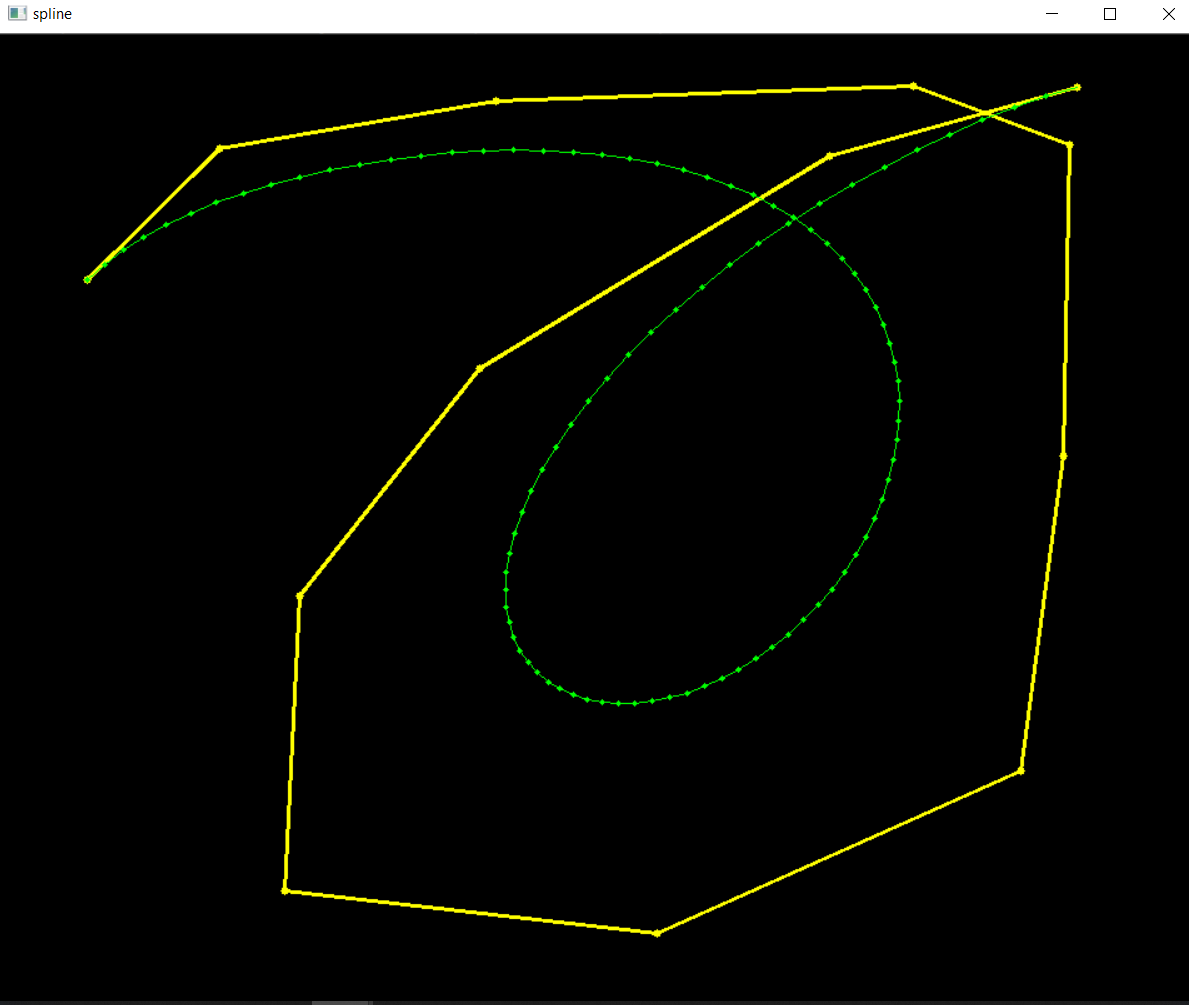
BSpline 

在数学的子学科数值分析里，B-样条是样条曲线一种特殊的表示形式。它是B-样条基曲线的线性组合。B-样条是贝兹（贝塞尔）曲线的一种一般化，可以进一步推广为非均匀有理B样条(NURBS)，使得我们能给更多一般的几何体建造精确的模型。

常数B样条

常数B样条是最简单的样条。只定义在一个节点距离上，而且不是节点的函数。它只是不同节点段（knot span）的标志函数（indicator function）。

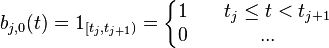
线性B样条

线性B样条定义在两个相邻的节点段上，在节点连续但不可微。

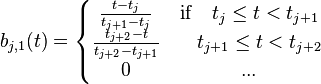
三次B样条

一个片断上的B样条的表达式可以写作：

 

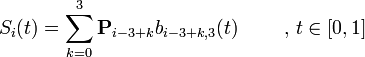
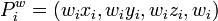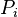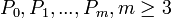 其中Si是第i个B样条片段，而P是一个控制点集，i和k是局部控制点索引。控制点的集合会是的集合，其中w_i是比重，当它增加时曲线会被拉向控制点，在减小时则把曲线远离该点。片段的整个集合m-2条曲线（S_3,S_4,...,S_m）由m+1个控制点（P_0,P_1,...,P_m, m \ge 3）定义，作为t上的一个B样条可以定义为

 

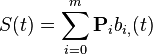
其中i是控制点数，t是取节点值的全局参数。这个表达式把B样条表示为B样条基函数的线性组合，这也是这个名称的原因。有两类B样条-均匀和非均匀。非均匀B样条相邻控制点间的距离不一定要相等。一个一般的形式是区间随着插入控制点逐步变小到0。

bspline.cpp核心代码

void BSpline::BuildWeights()
{
    ClearWeights();

    m_splineWeights = (double **)malloc(4 * sizeof(double*));
    m_tangentWeights = (double **)malloc(4 * sizeof(double*));

    for (int i = 0; i < 4; i++)
    {
        m_splineWeights[i] = (double*)malloc((m_subD) * sizeof(double));
        m_tangentWeights[i] = (double*)malloc((m_subD) * sizeof(double));
    }

    double u, u_2, u_3;
    for (int i = 0; i < m_subD; i++)
    {
        u = (float)i / m_subD;
        u_2 = u * u;
        u_3 = u_2 * u;

        // 参见"游戏编程精粹1"P331
        m_splineWeights[0][i] = (-1.0f*u_3 + 3.0f*u_2 - 3.0f*u + 1.0f) / 6.0f;
        m_splineWeights[1][i] = (3.0f*u_3 - 6.0f*u_2 + 0.0f*u + 4.0f) / 6.0f;
        m_splineWeights[2][i] = (-3.0f*u_3 + 3.0f*u_2 + 3.0f*u + 1.0f) / 6.0f;
        m_splineWeights[3][i] = (1.0f*u_3 + 0.0f*u_2 + 0.0f*u + 0.0f) / 6.0f;

        // 参见"游戏编程精粹1"P333
        m_tangentWeights[0][i] = (-1.0f*u_2 + 2.0f*u - 1.0f)*0.5f;
        m_tangentWeights[1][i] = (3.0f*u_2 - 4.0f*u + 0.0f)*0.5f;
        m_tangentWeights[2][i] = (-3.0f*u_2 + 2.0f*u + 1.0f)*0.5f;
        m_tangentWeights[3][i] = (1.0f*u_2 + 0.0f*u + 0.0f)*0.5f;
    }
}

显示效果如下

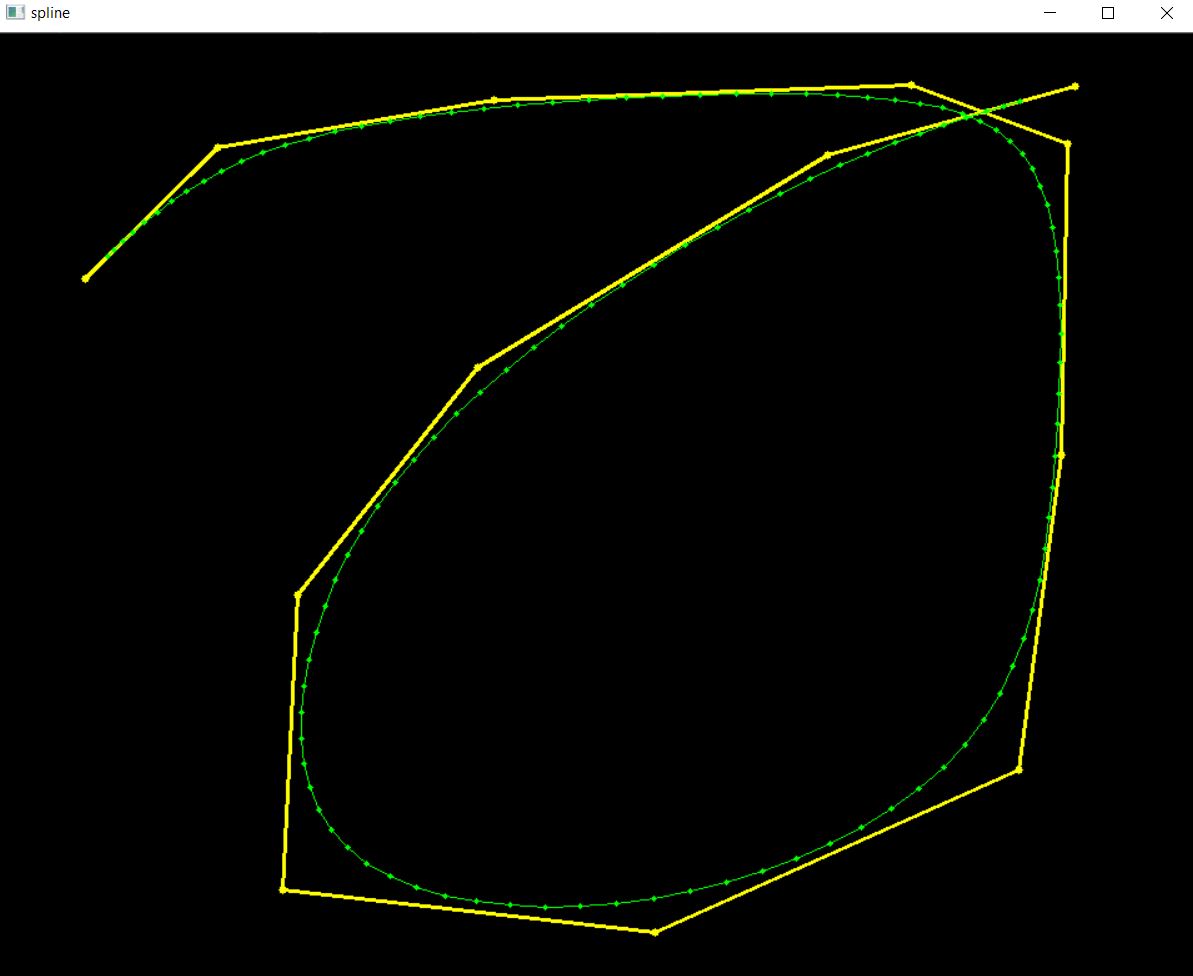
CatmullRoom

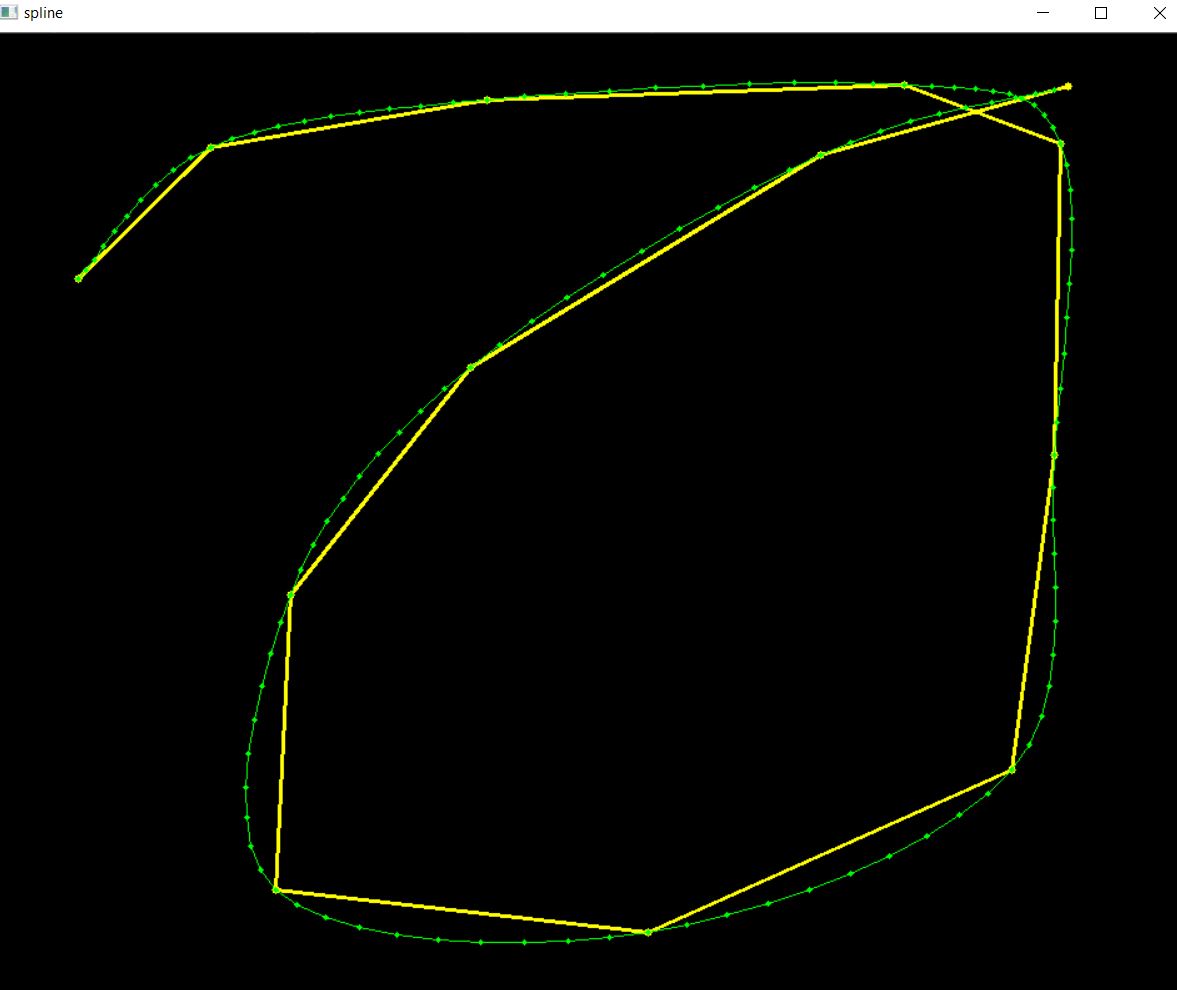
所谓样条曲线是指给定一组控制点而得到一条曲线，曲线的大致形状由这些点予以控制，一般可分为插值样条和逼近样条两种，插值样条通常用于数字化绘图或动画的设计，逼近样条一般用来构造物体的表面。CatmullRom样条与上一节所讲的B样条很相似，不同在于CatmullRom样条的曲线会经过其每一个控制点。

catmullroom.cpp核心代码入下

void CatmullRoom::BuildWeights()
{
    ClearWeights();

    m_splineWeights = (double **)malloc(4 * sizeof(double*));
    m_tangentWeights = (double **)malloc(4 * sizeof(double*));

    for (int i = 0; i < 4; i++)
    {
        m_splineWeights[i] = (double*)malloc((m_subD) * sizeof(double));
        m_tangentWeights[i] = (double*)malloc((m_subD) * sizeof(double));
    }

    double u, u_2, u_3;
    for (int i = 0; i < m_subD; i++)
    {
        u = (float)i / m_subD;
        u_2 = u * u;
        u_3 = u_2 * u;

        // 参见"游戏编程精粹1"P333
        m_splineWeights[0][i] = (-1.0f*u_3 + 2.0f*u_2 - 1.0f*u + 0.0f)*0.5f;
        m_splineWeights[1][i] = (3.0f*u_3 - 5.0f*u_2 + 0.0f*u + 2.0f)*0.5f;
        m_splineWeights[2][i] = (-3.0f*u_3 + 4.0f*u_2 + 1.0f*u + 0.0f)*0.5f;
        m_splineWeights[3][i] = (1.0f*u_3 - 1.0f*u_2 + 0.0f*u + 0.0f)*0.5f;

        m_tangentWeights[0][i] = (-3.0f*u_2 + 4.0f*u - 1.0f)*0.5f;
        m_tangentWeights[1][i] = (9.0f*u_2 - 10.0f*u + 0.0f)*0.5f;
        m_tangentWeights[2][i] = (-9.0f*u_2 + 8.0f*u + 1.0f)*0.5f;
        m_tangentWeights[3][i] = (3.0f*u_2 - 2.0f*u + 0.0f)*0.5f;
    }
}

 博主叶飞影博客附带可样条视化工具，可以下载设置控制点检测曲线效果。

B样条曲线上的最近点？

B样条曲线上的最近点？

如何解决B样条曲线上的最近点？？

该线程询问如何在给定同一平面上的任意点的情况下获得贝塞尔曲线上最近的点：Closest point on a cubic Bezier curve?

除了 B-SPline 曲线之外，我怎样才能完成同样的事情？

解决方法

暂无找到可以解决该程序问题的有效方法，小编努力寻找整理中！

如果你已经找到好的解决方法，欢迎将解决方案带上本链接一起发送给小编。

小编邮箱:dio#foxmail.com (将#修改为@）

B样条曲线方程和C++实现

B样条曲线方程和C++实现

功能：根据参数u值和k（大小为阶数值）与节点矢量，计算第i个k次B样条基数

输入参数： u—参数值；k—大小值为阶数；i—第i个k次B样条的支撑区间左端节点的下标；aNode为节点向量。

输出参数：返回函数值。

double GetBaseFunVal(double u, int i, int k, vector <double> m_aNode)

{

double Val = 0.0;

double Val1 = 0.0;

double Val2 = 0.0;

if (k==0)

{

if (u < m_aNode[i] || u > m_aNode[i+1])

return Val;

else

{

Val = 1.0;

return Val;

}

}

if (k>0)

{

if (u < m_aNode[i] || u > m_aNode[i+k+1])

{

return Val;

}

else

{

double alpha = 0.0;

double beta = 0.0;

double dTemp = 0.0;

dTemp = m_aNode[i+k] - m_aNode[i];

if (dTemp == 0.0)

{

alpha  = 0;

}

else

alpha = (u - m_aNode[i])/dTemp;

dTemp = m_aNode[i+k+1] - m_aNode[i+1];

 

if (dTemp == 0.0)

{

beta = 0.0;

}

else

beta = (m_aNode[i+k+1] - u)/dTemp;

Val1 = alpha * GetBaseFunVal(u, i, k-1, m_aNode);

Val2 = beta * GetBaseFunVal(u, i+1, k-1, m_aNode);

Val = Val1 + Val2;

}

}

 

return Val;

}

 

上述功能模块摘自于计算机辅助几何设计与非均匀有理B样条。已知B样条的n+1控制点坐标，以及相应的节点向量，可求得对应的曲线方程。

先计算各个控制点的基函数

 

 各个基函数的求解可根据上述的功能模块求出。

下面是我的C++实现：曲线是二维的，三维的情况，就Z坐标做同X,Y求解方式相同即可。在求解的过程中，我自己在CAD上画了个样条曲线，然后通过GetBaseFunVal(double u, int i, int k, vector <double> m_aNode)和顶点坐标，及节点向量求各个点的坐标。随着u值的变化，计算各个X,Y,Z值。一个星期的摸爬滚打中，能输出图形，但是与原来的图形对应不上。最终找到的原因在与基函数出问题了。在书本等相关资源中，基函数成员中的k表示的是次数，在我画的样条曲线中，阶数显示为3（为什么是3？CAD的标注里，实体块中的 70 下一行，为3），所以我理所当然的写为了2,。一直有问题。我将它改为3以后，竟然奇迹般的可以用了。而且跟原来图形吻合。这个是我的相关经历，希望对你们能有用。另外，哪位热心人士可以说明下，为什么k改为阶数大小，就可以呢？

#include <iostream>
#include <fstream>
#include <afxtempl.h>

using namespace std;

struct tPoint
{
    double x;
    double y;
    double z;
};


double GetBaseFunVal(double u, int i, int k, vector <double> m_aNode)
{
    double Val = 0.0;
    double Val1 = 0.0;
    double Val2 = 0.0;
    if (k==0)
    {
        if (u < m_aNode[i] || u > m_aNode[i+1])
            return Val;
        else
        {
            Val = 1.0;
            return Val;
        }
    }
    if (k>0)
    {
        if (u < m_aNode[i] || u > m_aNode[i+k+1])
        {
            return Val;
        }
        else
        {
            double alpha = 0.0;
            double beta = 0.0;
            double dTemp = 0.0;
            dTemp = m_aNode[i+k] - m_aNode[i];
            if (dTemp == 0.0)
            {
                alpha  = 0;
            }
            else
                alpha = (u - m_aNode[i])/dTemp;
            dTemp = m_aNode[i+k+1] - m_aNode[i+1];

            if (dTemp == 0.0)
            {
                beta = 0.0;
            }
            else
                beta = (m_aNode[i+k+1] - u)/dTemp;
            Val1 = alpha * GetBaseFunVal(u, i, k-1, m_aNode);
            Val2 = beta * GetBaseFunVal(u, i+1, k-1, m_aNode);
            Val = Val1 + Val2;
        }
    }

    return Val;
}

int main()
{
    tPoint tData;
    vector <tPoint> vtData;

    vtData.clear();
    vector <double> nodeVector;
    nodeVector.push_back(0);
    nodeVector.push_back(0);
    nodeVector.push_back(0);
    nodeVector.push_back(0);
    nodeVector.push_back(1);
    nodeVector.push_back(2);
    nodeVector.push_back(3);
    nodeVector.push_back(4);
    nodeVector.push_back(5);
    nodeVector.push_back(6);
    nodeVector.push_back(6);
    nodeVector.push_back(6);
    nodeVector.push_back(6);

    //节点向量nodeVector， 控制点坐标(0,3),(200,100), (750, 200), k=2

    for (double u = 0; u < 6; u=u+0.01)
    {
        // 样条的数据
        tData.x = (GetBaseFunVal(u, 0, 3, nodeVector)*(-7585) + GetBaseFunVal(u, 1, 3, nodeVector)*(-3427.5) + GetBaseFunVal(u, 2, 3, nodeVector)*46087.5
            + GetBaseFunVal(u, 3, 3, nodeVector)*9220.0 +  GetBaseFunVal(u, 4, 3, nodeVector)*(-14835.0) +  GetBaseFunVal(u, 5, 3, nodeVector)*(-2002.5) + GetBaseFunVal(u, 6, 3, nodeVector)*71975
            +  GetBaseFunVal(u, 7, 3, nodeVector)*45235 +  GetBaseFunVal(u, 8, 3, nodeVector)*83150)/*/(GetBaseFunVal(u, 0, 3, nodeVector) + GetBaseFunVal(u, 1, 3, nodeVector) + GetBaseFunVal(u, 2, 3, nodeVector)
            + GetBaseFunVal(u, 3, 3, nodeVector) +  GetBaseFunVal(u, 4, 3, nodeVector) +  GetBaseFunVal(u, 5, 3, nodeVector))*/;
         tData.y = (GetBaseFunVal(u, 0, 3, nodeVector)*(-3807.5) + GetBaseFunVal(u, 1, 3, nodeVector)*(19850.0) + GetBaseFunVal(u, 2, 3, nodeVector)*14335
             +  GetBaseFunVal(u, 3, 3, nodeVector)*(-17582.5) +  GetBaseFunVal(u, 4, 3, nodeVector)*(-5445.0) +  GetBaseFunVal(u, 5, 3, nodeVector)*(-80735.0) + GetBaseFunVal(u, 6, 3, nodeVector)*(-23817.5)
            +   GetBaseFunVal(u, 7, 3, nodeVector)*5037.5 +  GetBaseFunVal(u, 8, 3, nodeVector)*(-9360))/*/(GetBaseFunVal(u, 0, 3, nodeVector) + GetBaseFunVal(u, 1, 3, nodeVector) + GetBaseFunVal(u, 2, 3, nodeVector)
            + GetBaseFunVal(u, 3, 3, nodeVector) +  GetBaseFunVal(u, 4, 3, nodeVector) +  GetBaseFunVal(u, 5, 3, nodeVector))*/;
        tData.z = 0.0;

        vtData.push_back(tData);
    }

    char *file = "C:/Users/Monkey/Desktop/新建文件夹 (2)/TEST/Last.txt";
    ofstream out(file);
    if (!out)
    {
        cout << "打开文件失败！！！！" << endl;
    }  

    for (int n = 0; n < vtData.size(); n++)
    {
        out << vtData[n].x << "  " << vtData[n].y <<"   " << vtData[n].z << endl;
    }

    out.close();

    return 0;
}

 

原文出处：https://www.cnblogs.com/strangemonkey/p/11453959.html

今天关于计算极坐标中样条曲线的梯度和极坐标 梯度的讲解已经结束，谢谢您的阅读，如果想了解更多关于Android LineChart绘制多条曲线的方法、Bspline CatmullRoom and Bezier 样条曲线生成、B样条曲线上的最近点？、B样条曲线方程和C++实现的相关知识，请在本站搜索。

本文标签：

上一篇Python Pandas在dataFrame中计算百分比并将其放入列表的问题（pandas 如何求百分比）

下一篇用两个查询计算平均值（用两个查询计算平均值的函数）

相关文章