本文的目的是介绍PHP计算后序表达式的详细情况,特别关注逆波兰式的相关信息。我们将通过专业的研究、有关数据的分析等多种方式,为您呈现一个全面的了解PHP计算后序表达式的机会,同时也不会遗漏关于08.前
本文的目的是介绍PHP计算后序表达式的详细情况,特别关注逆波兰式的相关信息。我们将通过专业的研究、有关数据的分析等多种方式,为您呈现一个全面的了解PHP计算后序表达式的机会,同时也不会遗漏关于08. 前缀 (波兰表达式)、中缀、后缀表达式 (逆波兰表达式)、2021-10-17:逆波兰表达式求值。根据 逆波兰表示法,求表达式的值。有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:整数除法只保留整数部分。给定逆波兰、2022-11-05:给定一个逆波兰式,转化成正确的中序表达式。要求只有必要加括号的地方才加括号。、C++栈实现逆波兰式的应用的知识。
本文目录一览:- PHP计算后序表达式(逆波兰式)(php逆序输出)
- 08. 前缀 (波兰表达式)、中缀、后缀表达式 (逆波兰表达式)
- 2021-10-17:逆波兰表达式求值。根据 逆波兰表示法,求表达式的值。有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:整数除法只保留整数部分。给定逆波兰
- 2022-11-05:给定一个逆波兰式,转化成正确的中序表达式。要求只有必要加括号的地方才加括号。
- C++栈实现逆波兰式的应用

PHP计算后序表达式(逆波兰式)(php逆序输出)
百度谷歌搜索无果,只好自己造一次轮子。 PHP /** * rpn2value * 计算逆波兰式 * @author leo108 root@leo108.com */function rpn2value($str){ $arr = explode('','',$str); $stack = array(); $len = count($arr); for($i=0;$i$len;$i++){ if(is_numeric($ar
百度谷歌搜索无果,只好自己造一次轮子。 php
/**
* rpn2value
* 计算逆波兰式
* @author leo108 root@leo108.com
*/
function rpn2value($str){
$arr = explode('','',$str);
$stack = array();
$len = count($arr);
for($i=0;$i
<p>使用方法: </p><p>逆波兰式</p>
<pre>$str = "1,2,3,+,*,4,-,5,+,7,*";
echo rpn2value($str);另附中序转后序代码,版权归原作者所有 http://leo108.com/pid-1901.asp
/**
* math_rpn
*
* 实现逆波兰式算法
*
* @author sparkHuang 260558820@qq.com
* @version RPN 1.0.0
*
*/
class math_rpn {
//初始的计算表达式
private $_expression = '''';
//处理后的逆波兰表达式
private $_rpnexp = array();
//模拟栈结构的数组
private $_stack = array(''#'');
//正则判断
//private $_reg = ''/^([A-Za-z0-9\(\)\+\-\*\/])*$/'';
//优先级
private $_priority = array(''#'' => 0, ''('' => 10, ''+'' => 20, ''-'' => 20, ''*'' => 30, ''/'' => 30);
//四则运算
private $_operator = array(''('', ''+'', ''-'', ''*'', ''/'', '')'');
public function __construct($expression) {
$this->_init($expression);
}
private function _init($expression) {
$this->_expression = $expression;
}
public function exp2rpn() {
$len = strlen($this->_expression);
for($i = 0; $i _expression, $i, 1);
if ($char == ''('') {
$this->_stack[] = $char;
continue;
} else if ( ! in_array($char, $this->_operator)) {
$this->_rpnexp[] = $char;
continue;
} else if ($char == '')'') {
for($j = count($this->_stack); $j >= 0; $j--) {
$tmp = array_pop($this->_stack);
if ($tmp == "(") {
break;
} else {
$this->_rpnexp[] = $tmp;
}
}
continue;
} else if ($this->_priority[$char] _priority[end($this->_stack)]) {
$this->_rpnexp[] = array_pop($this->_stack);
$this->_stack[] = $char;
continue;
} else {
$this->_stack[] = $char;
continue;
}
}
for($i = count($this->_stack); $i >= 0; $i--) {
if (end($this->_stack) == ''#'') break;
$this->_rpnexp[] = array_pop($this->_stack);
}
return $this->_rpnexp;
}
}
//测试实例
$expression = "(A*(B+C)-E+F)*G";
var_dump($expression);
$mathrpn = new math_rpn($expression);
var_dump($mathrpn->exp2rpn());
中序表达式

08. 前缀 (波兰表达式)、中缀、后缀表达式 (逆波兰表达式)
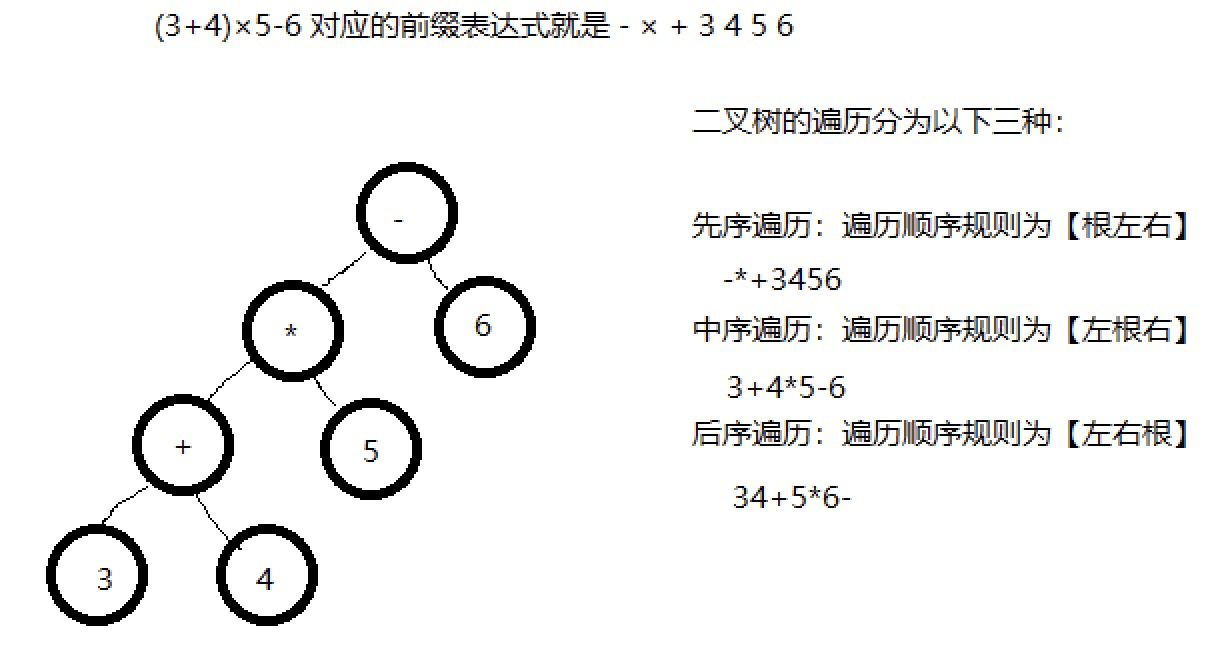
前缀表达式的求值:
例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:
- 从右至左扫描,将 6、5、4、3 压入堆栈
- 遇到 + 运算符,因此弹出 3 和 4(3 为栈顶元素,4 为次顶元素),计算出 3+4 的值,得 7,再将 7 入栈
- 接下来是 × 运算符,因此弹出 7 和 5,计算出 7×5=35,将 35 入栈
- 最后是 - 运算符,计算出 35-6 的值,即 29,由此得出最终结果
将中缀表达式转成后缀表达式:
(1)初始化两个栈:运算符栈s1和储存中间结果的栈s2;
(2)从左至右扫描中缀表达式;
(3)遇到操作数时,将其压s2;
(4)遇到运算符时,比较其与s1栈顶运算符的优先级:
1.如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
2.若优先级比栈顶运算符的高,也将运算符压入s1,否则将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中新的栈顶运算符相比较;
(5)遇到括号时:
1.如果是左括号“(”,则直接压入s1
2.如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
(6)重复步骤2至5,直到表达式的最右边
(7)将s1中剩余的运算符依次弹出并压入s2
(8)依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式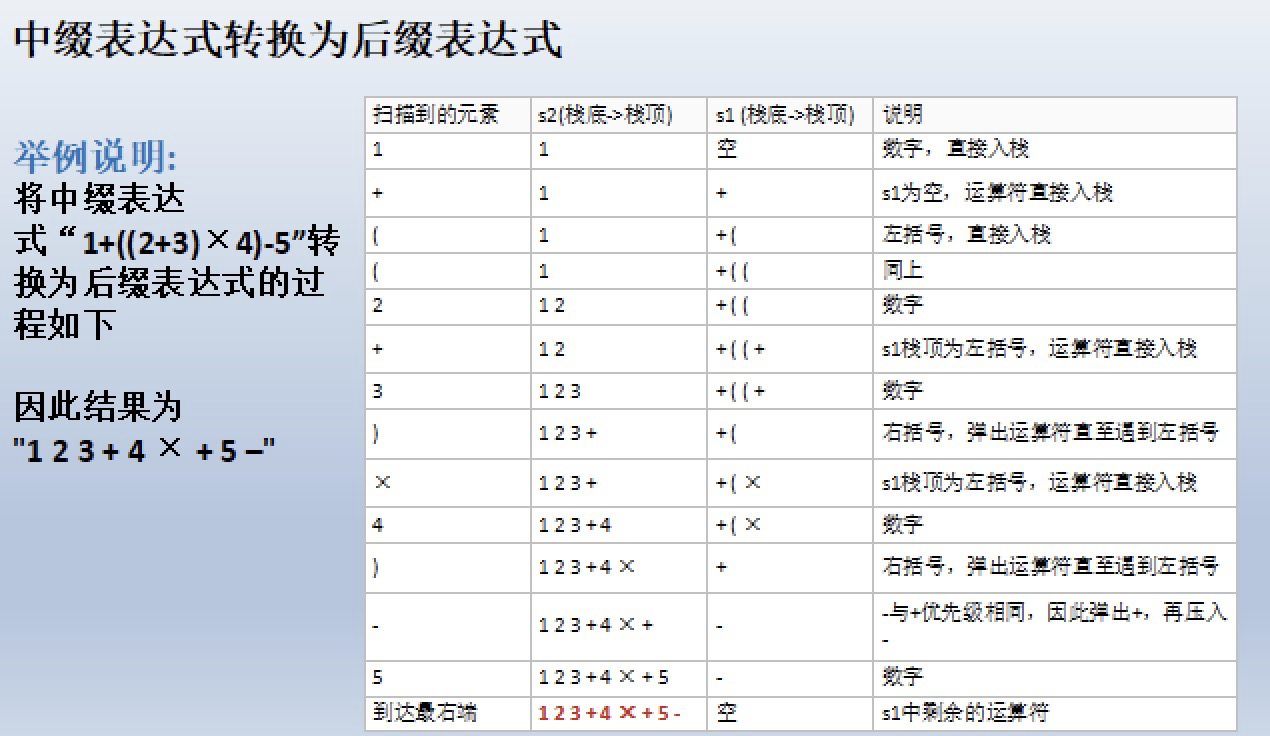
import java.math.BigDecimal;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
import java.util.regex.Pattern;
/**
* 逆波兰整数计算器
*/
public class PolandNotation {
public static boolean isNumber(String s){
Pattern pattern = Pattern.compile("^[-+]?[.\\d]+$");
return pattern.matcher(s).matches();
}
//中缀表达式转化为list
public static List<String> toInfixList(String s){
if (s==null) throw new RuntimeException("空表达式");
if (String.valueOf(s.charAt(0)).equals(")")) throw new RuntimeException("错误的表达式");
//\\s+匹配任何空白字符,包括空格、制表符、换页符等,等价[\f\n\r\t\v]
s = s.replaceAll("\\s+","");
System.out.println(s);
List<String> list = new ArrayList<>();
int i = 0;
char c;
String str = "";
do {
c = s.charAt(i);
//不是数字并且不是.
if (String.valueOf(c).matches("[\\D]")&&!String.valueOf(c).equals(".")){
if (i==0&&(!String.valueOf(c).equals("("))){//第一个字符不是(拼接到str
str += c;
}else if (i!=0&&String.valueOf(c).equals("-")&&String.valueOf(s.charAt(i-1)).equals("(")){//非第一个字符,根据前一个是否是(判断是负号还上减号
str += c;
}else {
list.add(String.valueOf(c));
}
i++;
}else {
while (i<s.length()&&String.valueOf(c=s.charAt(i)).matches("[\\d.]")){//是符号或是小数点
str += c;
i++;
}
int a = str.indexOf(".");
if (a!=-1){
if (str.indexOf(".",a+1)!=-1) throw new RuntimeException("数字中保含多个小数点");
}
if (!String.valueOf(str.charAt(0)).matches("[-\\d]")){
str = str.substring(1);
}
list.add(str);
str = "";
}
}while (i<s.length());
return list;
}
//中缀表达式列表改为后缀表达式列表
public static List<String> parseSuffixList(List<String> list){
Stack<String> s1 = new Stack<>();
List<String> s2 = new Stack<>();
for (String item:list) {
if (isNumber(item)){
s2.add(item);
}else if (item.equals("(")){
s1.push(item);
}else if (item.equals(")")){//遇到)就将s1中的弹出加入s2,直到遇到s1的(
while (!s1.peek().equals("(")){
s2.add(s1.pop());
}
s1.pop();//弹出s1的(
}else { //遇到符号了,看s1栈顶运算符,s1的优先级不小于它,就弹出放入s2,再与s1栈顶运算符比较,否则将这个符号放入s1
while (s1.size()!=0&&(getValue(s1.peek())>=getValue(item))){
s2.add(s1.pop());
}
s1.push(item);
}
}
//将s1中剩下的运算符依次弹出到s2
while (s1.size()!=0){
s2.add(s1.pop());
}
return s2;
}
public static int getValue(String oper){
if (oper.equals("*")||oper.equals("×")||oper.equals("/")){
return 2;
}else if (oper.equals("+")||oper.equals("-")){
return 1;
}else {
return -1;
}
}
public static String calculate(List<String> list){
Stack<String> stack = new Stack<>();
for (String item : list) {
if (isNumber(item)){
stack.push(item);
}else {
String s2 = stack.pop();
String s1 = stack.pop();
BigDecimal res = BigDecimal.ZERO;
BigDecimal b2 = new BigDecimal(s2);
BigDecimal b1 = new BigDecimal(s1);
if (item.equals("+")){
res = b1.add(b2);
}else if (item.equals("-")){
res = b1.subtract(b2);
}else if (item.equals("*")||item.equals("×")){
res = b1.multiply(b2);
}else if (item.equals("/")){
res = b1.divide(b2,BigDecimal.ROUND_HALF_UP);
}else {
throw new RuntimeException("运算符错误");
}
stack.push(String.valueOf(res));
}
}
return stack.pop();
}
public static void main(String[] args){
List<String> strings = toInfixList("-1+((-30 . 1- 4)×5 /5+1)- 6");//[-1, +, (, (, -30.1, -, 4, ), ×, 5, /, 5, +, 1, ), -, 6]
System.out.println("strings2.toString() = " + strings.toString());
List<String> strings2 = parseSuffixList(strings);
System.out.println("strings2.toString() = " + strings2.toString());//[-1, -30.1, 4, -, 5, ×, 5, /, 1, +, +, 6, -]
String calculate = calculate(strings2);
System.out.println(calculate);//-40.1
}
}

2021-10-17:逆波兰表达式求值。根据 逆波兰表示法,求表达式的值。有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:整数除法只保留整数部分。给定逆波兰
2021-10-17:逆波兰表达式求值。根据 逆波兰表示法,求表达式的值。有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:整数除法只保留整数部分。给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。力扣 150。
福大大 答案 2021-10-17:
栈。遇到数字,压栈。遇到运算符,计算。
时间复杂度:O (N)。
空间复杂度:O (N)。
代码用 golang 编写。代码如下:
package main
import (
"fmt"
"strconv"
)
func main() {
tokens := []string{
"2", "1", "+", "3", "*"}
ret := evalRPN(tokens)
fmt.Println(ret)
}
func evalRPN(tokens []string) int {
stack := make([]int, 0)
for _, str := range tokens {
if str == "+" || str == "-" || str == "*" || str == "/" {
compute(&stack, str)
} else {
i, _ := strconv.Atoi(str)
stack = append(stack, i)
}
}
return stack[len(stack)-1]
}
func compute(stack *[]int, op string) {
num2 := (*stack)[len(*stack)-1]
*stack = (*stack)[0 : len(*stack)-1]
num1 := (*stack)[len(*stack)-1]
*stack = (*stack)[0 : len(*stack)-1]
ans := 0
switch op {
case "+":
ans = num1 + num2
break
case "-":
ans = num1 - num2
break
case "*":
ans = num1 * num2
break
case "/":
ans = num1 / num2
break
}
*stack = append(*stack, ans)
}执行结果如下:
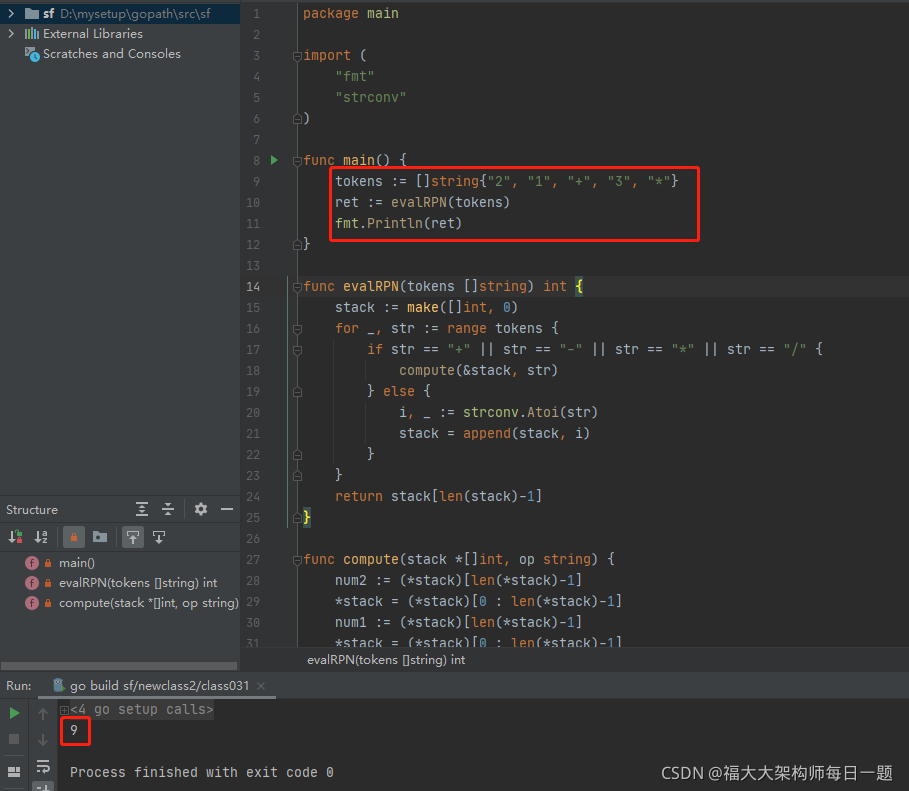
左神 java 代码

2022-11-05:给定一个逆波兰式,转化成正确的中序表达式。要求只有必要加括号的地方才加括号。
2022-11-05:给定一个逆波兰式,转化成正确的中序表达式。要求只有必要加括号的地方才加括号。
答案 2022-11-05:
代码用 rust 编写。代码如下:
计算结果。用栈。遇到数字,入栈;遇到运算符,出栈。 给出表达式,难点在于去掉没必要的小括号。准备两个栈,一个栈存数字,另一个栈存类型,类型有数字类型,加减类型,乘除类型。最有可能加括号的一定是后来的乘除类型遇到先来的加减类型。
执行结果如下:
fn main() {
let rpn = "3 -5 13 + * 6 2 3 - 2 + / + 4 5 3 * * -";
println!("{}", get_ans(rpn));
println!("{}", convert(rpn));
}
// 请保证给定的逆波兰式是正确的!
fn get_ans(rpn: &str) -> i32 {
if rpn == "" {
return 0;
}
let parts: Vec<&str> = rpn.split(" ").collect();
let mut stack: Vec<i32> = vec![];
for part in parts.iter() {
if *part == "+" || *part == "-" || *part == "*" || *part == "/" {
let right = stack.pop().unwrap();
let left = stack.pop().unwrap();
let mut ans: i32 = 0;
if *part == "+" {
ans = left + right;
} else if *part == "-" {
ans = left - right;
} else if *part == "*" {
ans = left * right;
} else {
ans = left / right;
}
stack.push(ans);
} else {
let a: i32 = part.parse().unwrap();
stack.push(a);
}
}
// stack 只有一个数,最终的结果
return stack.pop().unwrap();
}
#[derive(PartialEq)]
enum Operation {
SingleNumber,
AddOrMinus,
MultiplyOrDivide,
}
// 请保证输入的逆波兰式是正确的
// 否则该函数不保证正确性
// 逆波兰式仅支持+、-、*、/
// 想支持更多算术运算符自己改
fn convert(rpn: &str) -> String {
if rpn == "" {
return String::from("");
}
let parts: Vec<&str> = rpn.split(" ").collect();
let mut stack1: Vec<String> = vec![];
let mut stack2: Vec<Operation> = vec![];
for cur in parts.iter() {
// cur 当前遇到的字符串
// +- */ 单数
if *cur == "+" || *cur == "-" {
let b = stack1.pop().unwrap();
let a = stack1.pop().unwrap();
stack2.pop();
stack2.pop();
stack1.push(format!("{}{}{}", a, cur, b));
stack2.push(Operation::AddOrMinus);
} else if *cur == "*" || *cur == "/" {
let b = stack1.pop().unwrap();
let a = stack1.pop().unwrap();
let b_op = stack2.pop().unwrap();
let a_op = stack2.pop().unwrap();
let left = if a_op == Operation::AddOrMinus {
format!("({})", a)
} else {
a
};
let right = if b_op == Operation::AddOrMinus {
format!("({})", b)
} else {
b
};
stack1.push(format!("{}{}{}", left, cur, right));
stack2.push(Operation::MultiplyOrDivide);
} else {
stack1.push(String::from(*cur));
stack2.push(Operation::SingleNumber);
}
}
return String::from(stack1.pop().unwrap());
}
执行结果如下:
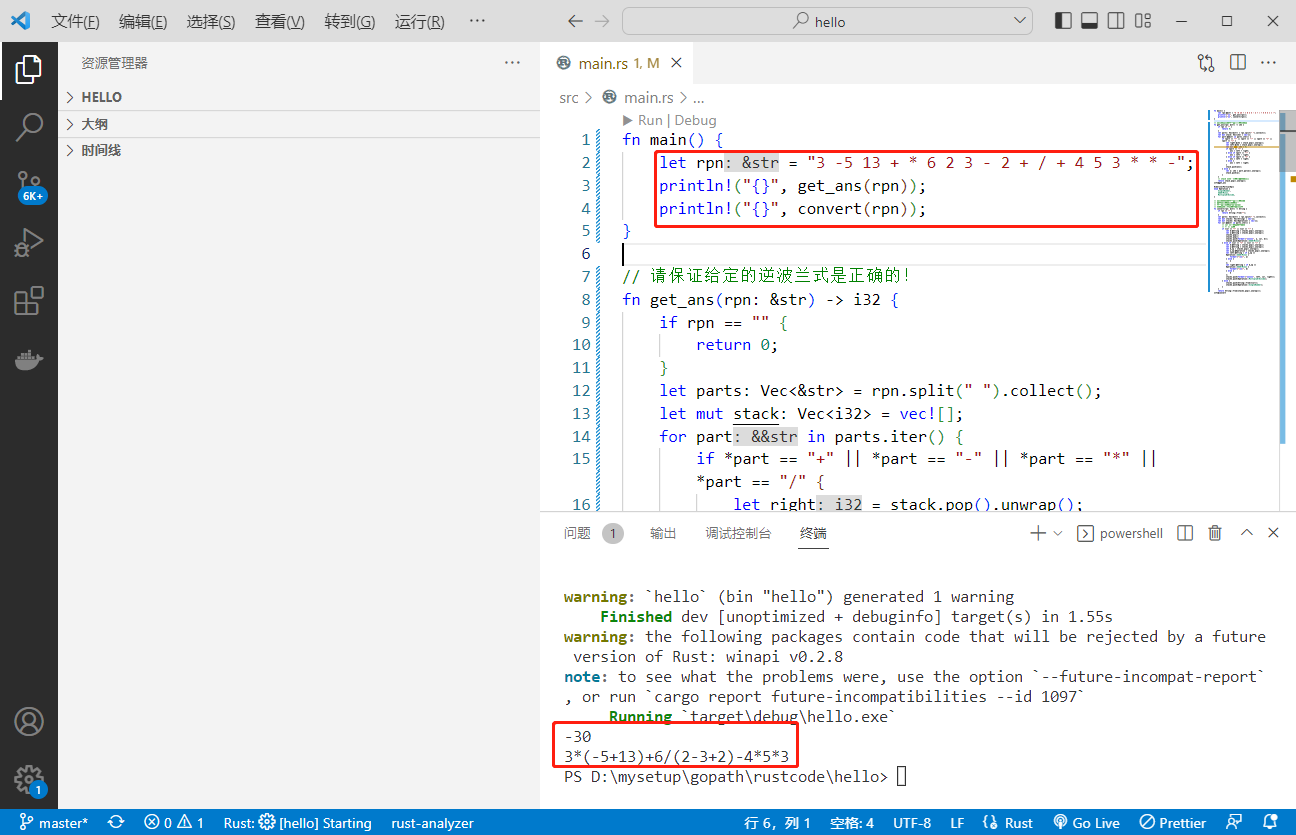
左神 java 代码

C++栈实现逆波兰式的应用
一.定义
逆波兰式,又称后缀表达式,指的是操作符在其所控制的操作数后面的表达式。
举个例子,1 + 2 * 3 - 4这个表达式是我们熟悉的中缀表达式,那么其所对应的后缀表达式为:1 2 3 * + 4 -。
再来个复杂的例子:1 * (2 + 3) / 5 - 4 / 2其对应的后缀表达式为:1 2 3 + * 5 / 4 2 / -(其中括号由于只是提升表达式优先级的作用,因此不放入后缀表达式中)。
二.逆波兰式的意义
为什么要将看似简单的中缀表达式转换为复杂的逆波兰式,原因就在于这个简单是相对我们人类的思维结构来说的,对计算机而言中序表达式是非常复杂的结构。相对的,逆波兰式在计算机看来却是比较简单易懂的结构。因为计算机普遍采用的内存结构是栈式结构,它执行先进后出的顺序。
三.逆波兰式的实现
1.方法
(1)中缀表达式转化为后缀表达式
对于给出的中缀表达式,如何将其转化为后缀表达式呢?
第一,若遇到操作数则直接输出/存储。
第二,遇到操作符,若此时栈为空或者操作符优先级高于栈顶,则入栈。
第三,若操作符的优先级低于或者等于栈顶,则出栈直至栈空或者优先级低于该操作符。
第四,遇到''('',其后的所有操作符(直至遇到'')'')按上述操作入栈或出栈;当遇到'')‘时,将''(''顶上的所有操作符出栈。

(2)由后缀表达式计算结果
第一,遇到操作数则入栈。
第二,遇到操作符则将栈顶的两个操作数出栈,其中第一个数为右操作数,第二个数为左操作数。
第三,计算结果并将计算的结果入栈。
第四,最后栈顶的结果即为所计算的结果。

2.代码实现
#include <iostream>
#include <string>
#include <stack>
#include <vector>
using namespace std;
string trans(string& s)
{
string operand;
stack<char> Operator;
int flag = 0;//记录括号优先级
for (const auto& e : s)
{
if (e == ''('')
{
Operator.push(e);
flag = 1;
continue;
}
if (e == '')'')
{
flag = 0;
while (Operator.top() != ''('')
{
operand.push_back(Operator.top());
Operator.pop();
}
Operator.pop();
continue;
}
//操作符
if (e == ''+'' || e == ''-'' || e == ''*'' || e == ''/'')
{
if (flag == 1)
{
if (Operator.top() == ''('')
{
Operator.push(e);
}
else if ((e == ''*'' || e == ''/'') && (Operator.top() == ''+'' || Operator.top() == ''-''))
{
Operator.push(e);
}
else//操作符的优先级低于或等于栈顶操作符则出栈,直至遇到''(''
{
while (Operator.top() != ''('')
{
operand.push_back(Operator.top());
Operator.pop();
}
Operator.push(e);
}
}
else if (Operator.empty())//栈空就入栈
{
Operator.push(e);
}
//操作符的优先级高于栈顶操作符,入栈
else if ((e == ''*'' || e == ''/'') && (Operator.top() == ''+'' || Operator.top() == ''-''))
{
Operator.push(e);
}
else//操作符的优先级低于或等于栈顶操作符则出栈,直至栈空或者优先级高于栈顶操作符
{
while (!Operator.empty())
{
operand.push_back(Operator.top());
Operator.pop();
}
Operator.push(e);
}
}
//操作数
else
{
operand.push_back(e);
}
}
while (!Operator.empty())
{
operand.push_back(Operator.top());
Operator.pop();
}
return operand;
}
int evalRPN(const string& s)
{
stack<char> operand;
int left = 0, right = 0;
for (const auto& e : s)
{
if (e == ''+'' || e == ''-'' || e == ''*'' || e == ''/'')
{
switch (e)
{
case ''+'':
right = operand.top();
operand.pop();
left = operand.top();
operand.pop();
operand.push(left + right);
break;
case ''-'':
right = operand.top();
operand.pop();
left = operand.top();
operand.pop();
operand.push(left - right);
break;
case ''*'':
right = operand.top();
operand.pop();
left = operand.top();
operand.pop();
operand.push(left * right);
break;
case ''/'':
right = operand.top();
operand.pop();
left = operand.top();
operand.pop();
operand.push(left / right);
break;
}
}
else//操作数
{
operand.push(e - ''0'');
}
}
return operand.top();
}
int RPN(const string& str)
{
//1.中缀表达式转化为后缀表达式
string s(str);
s = trans(s);
//2.后缀表达式计算答案
return evalRPN(s);
}
int main()
{
string s("1*(2*3+5)/5-4/2");
int ret = RPN(s);
cout << "ret:" << ret << endl;
return 0;
}
结果:

到此这篇关于C++栈实现逆波兰式的应用的文章就介绍到这了,更多相关C++ 逆波兰式内容请搜索以前的文章或继续浏览下面的相关文章希望大家以后多多支持!
- C++代码实现逆波兰式
- C++实现逆波兰式
我们今天的关于PHP计算后序表达式和逆波兰式的分享就到这里,谢谢您的阅读,如果想了解更多关于08. 前缀 (波兰表达式)、中缀、后缀表达式 (逆波兰表达式)、2021-10-17:逆波兰表达式求值。根据 逆波兰表示法,求表达式的值。有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:整数除法只保留整数部分。给定逆波兰、2022-11-05:给定一个逆波兰式,转化成正确的中序表达式。要求只有必要加括号的地方才加括号。、C++栈实现逆波兰式的应用的相关信息,可以在本站进行搜索。
本文标签:





