本文的目的是介绍POJ-3436:ACMComputerFactory的详细情况,特别关注Dinic最大流的相关信息。我们将通过专业的研究、有关数据的分析等多种方式,为您呈现一个全面的了解POJ-34
本文的目的是介绍POJ-3436:ACM Computer Factory 的详细情况,特别关注Dinic 最大流的相关信息。我们将通过专业的研究、有关数据的分析等多种方式,为您呈现一个全面的了解POJ-3436:ACM Computer Factory 的机会,同时也不会遗漏关于18.10.29 POJ 3987 Computer Virus on Planet Pandora(AC自动机+字符串处理)、2020 杭电多校第四场 1007 Go Running Dinic 最大流跑二分图匹配、AC 的故事大结局山寨版(下)(网络流之最大流,当前弧优化的 dinic)、ACM-ICPC Beijing 2016 Genius ACM(倍增 + 二分)的知识。
本文目录一览:- POJ-3436:ACM Computer Factory (Dinic 最大流)(最大流定义)
- 18.10.29 POJ 3987 Computer Virus on Planet Pandora(AC自动机+字符串处理)
- 2020 杭电多校第四场 1007 Go Running Dinic 最大流跑二分图匹配
- AC 的故事大结局山寨版(下)(网络流之最大流,当前弧优化的 dinic)
- ACM-ICPC Beijing 2016 Genius ACM(倍增 + 二分)

POJ-3436:ACM Computer Factory (Dinic 最大流)(最大流定义)
题目链接:http://poj.org/problem?id=3436
解题心得:
- 题目真的是超级复杂,但解出来就是一个网络流,建图稍显复杂。其实提炼出来就是一个工厂 n 个加工机器,每个机器有一个效率 w,q 个材料入口,q 个材料出口,每个口有三个数表示状态,1 表示一定有入 / 出的材料,0 表示没有入 / 出的材料,2 表示可能有入的材料。如果一个机器入口全是 0,代表这是起始机器,如果一个机器出口全是 1,那么代表这是末尾机器。
- 具体做法:
- 将每个机器 i 拆成两点 i 和 i+n 分别代表进和出
- 建立超级源点,连在起始机器上,流量 INF。 建立超级汇点,找到末尾机器连在超级汇点上,流量 INF。
- 一个机器拆成的两个点 i 和 i+n 连上,流量就是这个点的效率 w。
- 然后暴力匹配,看一个点的所有出口是否可以完全对应一个点的入口,如果可以,匹配上,流量 INF。
- 跑 Dinic,得到最大流。
- 刚开始看到这个题没啥思路,因为关系太过于复杂,但是只要将题目中所有的关系提炼出来,就很容易建立一个网络图,要整体效率最大,那就是跑一个最大流啊,但是如果关系找漏 GG。
#include <stdio.h>
#include <cstring>
#include <stdlib.h>
#include <queue>
#include <math.h>
#include <vector>
#include <climits>
using namespace std;
const int maxn = 1e4+7;
const int INF = INT_MAX;
int p, n, S, T, level[maxn], iter[maxn];
struct Machine {
int in[15];
int out[15];
int p;
}m[maxn];
struct Edge {
int to, cap, rev, flow;
Edge(int To, int Cap, int Rev, int Flow):
to(To), cap(Cap), rev(Rev), flow(Flow){}
};
vector <Edge> ve[maxn];
void add_edge(int s,int t, int cap) {//建边
ve[s].push_back(Edge(t, cap, ve[t].size(), 0));
ve[t].push_back(Edge(s, 0, ve[s].size()-1, 0));
}
void build_edge() {//找出口和入口的关系
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
if(i == j)
continue;
bool flag = false;
for(int k=1;k<=p;k++) {
if(m[j].in[k] != 2 && m[i].out[k] != m[j].in[k]) {
flag = true;
break;
}
}
if(!flag)
add_edge(i+n, j, INF);
}
add_edge(i, i+n, m[i].p);
}
}
void init() {
scanf("%d%d",&p,&n);
S = 0, T = 2*n + 1;
for(int i=1;i<=n;i++) {//找起始机器和末尾机器
scanf("%d", &m[i].p);
bool flag = false;
for (int j = 1; j <= p; j++) {
scanf("%d", &m[i].in[j]);
if (m[i].in[j] == 1)
flag = true;
}
if (!flag)
add_edge(S, i, INF);
flag = false;
for (int j = 1; j <= p; j++) {
scanf("%d", &m[i].out[j]);
if (m[i].out[j] != 1)
flag = true;
}
if (!flag)
add_edge(i+n, T, INF);
}
build_edge();
}
bool bfs() {
memset(level, -1, sizeof(level));
level[S] = 0;
queue <int> qu;
qu.push(S);
while(!qu.empty()) {
int now = qu.front(); qu.pop();
for(int i=0; i<ve[now].size(); i++) {
Edge &e = ve[now][i];
if(e.cap > e.flow && level[e.to] < 0) {
level[e.to] = level[now] + 1;
qu.push(e.to);
}
}
}
return level[T] > 0;
}
int dfs(int now, int f) {
if(now == T) return f;
for(int &i=iter[now]; i<ve[now].size(); i++) {
Edge &e = ve[now][i];
if(e.cap > e.flow && level[e.to] > level[now]) {
int d = dfs(e.to, min(f, e.cap-e.flow));
if(d > 0) {
e.flow += d;
ve[e.to][e.rev].flow -= d;
return d;
}
}
}
return 0;
}
int max_flow() {//Dinic跑最大流
int ans = 0;
while(bfs()) {
int f = dfs(S, INF);
memset(iter, 0, sizeof(iter));
if(f > 0)
ans += f;
else
break;
}
return ans;
}
int cnt, path[maxn][5];
void Print_path(int ans) {//把路找出来
cnt = 0;
for(int i=n+1;i<=2*n;i++) {
for(int j=0;j<ve[i].size();j++) {
Edge &e = ve[i][j];
if(e.flow > 0 && e.to <= n) {
path[cnt][0] = i - n;
path[cnt][1] = e.to;
path[cnt][2] = e.flow;
cnt++;
}
}
}
printf("%d %d\n",ans, cnt);
for(int i=0;i<cnt;i++)
printf("%d %d %d\n",path[i][0], path[i][1], path[i][2]);
}
int main() {
init();
int ans = max_flow();
Print_path(ans);
}

18.10.29 POJ 3987 Computer Virus on Planet Pandora(AC自动机+字符串处理)
描述
Aliens on planet Pandora also write computer programs like us. Their programs only consist of capital letters (‘A’ to ‘Z’) which they learned from the Earth. On planet Pandora, hackers make computer virus, so they also have anti-virus software. Of course they learned virus scanning algorithm from the Earth. Every virus has a pattern string which consists of only capital letters. If a virus’s pattern string is a substring of a program, or the pattern string is a substring of the reverse of that program, they can say the program is infected by that virus. Give you a program and a list of virus pattern strings, please write a program to figure out how many viruses the program is infected by.输入There are multiple test cases. The first line in the input is an integer T ( T <= 10) indicating the number of test cases.
For each test case:
The first line is a integer n( 0 < n <= 250) indicating the number of virus pattern strings.
Then n lines follows, each represents a virus pattern string. Every pattern string stands for a virus. It’s guaranteed that those n pattern strings are all different so there are n different viruses. The length of pattern string is no more than 1,000 and a pattern string at least consists of one letter.
The last line of a test case is the program. The program may be described in a compressed format. A compressed program consists of capital letters and “compressors”. A “compressor” is in the following format:
[qx]
q is a number( 0 < q <= 5,000,000)and x is a capital letter. It means q consecutive letter xs in the original uncompressed program. For example, [6K] means ‘KKKKKK’ in the original program. So, if a compressed program is like:
AB[2D]E[7K]G
It actually is ABDDEKKKKKKKG after decompressed to original format.
The length of the program is at least 1 and at most 5,100,000, no matter in the compressed format or after it is decompressed to original format.输出For each test case, print an integer K in a line meaning that the program is infected by K viruses.
样例输入
3
2
AB
DCB
DACB
3
ABC
CDE
GHI
ABCCDEFIHG
4
ABB
ACDEE
BBB
FEEE
A[2B]CD[4E]F
样例输出
0
3
2
提示
In the second case in the sample input, the reverse of the program is ‘GHIFEDCCBA’, and ‘GHI’ is a substring of the reverse, so the program is infected by virus ‘GHI’.


1 #include <iostream>
2 #include <string.h>
3 #include <algorithm>
4 #include <stack>
5 #include <string>
6 #include <math.h>
7 #include <queue>
8 #include <stdio.h>
9 #include <string.h>
10 #include <vector>
11 #include <fstream>
12 #include <set>
13
14 using namespace std;
15 const int maxn = 255;
16 char line[5100005];
17 int kase, n, infecsum = 0, nodecou,l;
18 struct node {
19 node*next[26];
20 node*prev;
21 int count;
22 node() {
23 memset(next, 0, sizeof(next));
24 prev = NULL;
25 count = 0;
26 }
27 }tree[maxn * 1000];
28
29 void build() {
30 for (int i = 0; i < 26; i++)
31 tree[0].next[i] = tree + 1;
32 tree[0].prev = NULL;
33 tree[1].prev = tree;
34 queue<node*>q;
35 q.push(tree + 1);
36 while (!q.empty()) {
37 node*now = q.front();
38 q.pop();
39 for (int i = 0; i < 26; i++) {
40 node*child = now->next[i];
41 if (child) {
42 node*prev = now->prev;
43 while (prev->next[i] == NULL)
44 prev = prev->prev;
45 child->prev = prev->next[i];
46 q.push(child);
47 }
48 }
49 }
50 }
51
52 int search(char *str) {
53 int ans = 0;
54 node*first = tree + 1;
55 for (int i = 0; str[i] != ''\0''; i++) {
56 while (first->next[str[i] - ''A''] == NULL&&first!=(tree+1))
57 first = first->prev;
58 if (first->next[str[i] - ''A''])
59 first = first->next[str[i] - ''A''];
60 node*tmp = first;
61 while (tmp != NULL && tmp->count != -1) {
62 ans += tmp->count;
63 tmp->count = -1;
64 tmp = tmp->prev;
65 }
66 }
67 return ans;
68 }
69
70 void insert(node*rt, char* line) {
71 int l = strlen(line);
72 for (int i = 0; i < l; i++) {
73 if (rt->next[line[i] - ''A''] == NULL) {
74 nodecou++;
75 rt->next[line[i] - ''A''] = tree + nodecou;
76 }
77 rt = rt->next[line[i] - ''A''];
78 }
79 rt->count++;
80 }
81
82 void stringin() {
83 char ch;
84 scanf("\n");
85 while (scanf("%c", &ch)) {
86 if (ch == ''\n'')
87 break;
88 if (ch == ''['') {
89 int c;
90 scanf("%d", &c);
91 scanf("%c", &ch);
92 for (int i = 1; i <= c; i++)line[l++] = ch;
93 scanf("%c", &ch);
94 }
95 else
96 line[l++] = ch;
97 }
98 line[l] = ''\0'';
99 }
100
101 void init() {
102 scanf("%d", &kase);
103 while (kase--) {
104 memset(tree, 0, sizeof(tree));
105 infecsum = 0, nodecou = 1,l=0;
106 scanf("%d", &n);
107 for (int i = 1; i <= n; i++) {
108 scanf("%s",line);
109 insert(tree + 1, line);
110 }
111 build();
112 stringin();
113 infecsum=search(line);
114 reverse(line,line+l);
115 infecsum+=search(line);
116 printf("%d\n", infecsum);
117 }
118 }
119
120 int main()
121 {
122 init();
123 return 0;
124 }这题杀我……!
果然自动AC什么的都是假的QwQ
一开始倔强地使用了string结果无限TLE
后来又因为中间少了一句迭代而WA
die了
再也不想看到这道题
开学来做得最悲伤的一道题没有之一
主要是要考虑子串中套子串的问题如果不加标记会TLE(我看见有人没有考虑AC了??逗我??)
稍微处理一下字符串

2020 杭电多校第四场 1007 Go Running Dinic 最大流跑二分图匹配
题目
题目链接
题目大意是这样的:在一条双向的轴上,有若干同学在跑步,每位同学的速度是固定的,都是 1 单位长度 /s。在 n 个时刻 t,位置
x 上将至少有一个人在跑步,但是方向不确定,仅能确定有人。
需要求解的问题就是根据这 n 个时刻的信息,问能确定最少有多少同学在跑步?
二分图匹配
首先这个问题,以时间为横轴,位置为纵轴建系 x-t 图像,将 n 个数据描点。
题目中提到学生跑步有起始时间和终止时间,反映在坐标系上就是一条线段。但是由于题目要求的是最小的学生数量,因此不妨假设学生跑步时间是无限长,且开始的无限早,这反映在坐标系上就是一条直线。
也就是说倘若一个学生在向正方向跑,那么其跑出的直线斜率为 1,反之斜率为 - 1。
如果两个点描述的是同一个学生,那么这两个点就在同一条直线上。
那么问题就转变成了给定 n 个点,使用斜率为 1 或者 - 1 的直线覆盖这些点,问最少直线数量是多少?
斜率为 - 1 或 1 不太好处理,我们不妨将坐标轴顺时针旋转 45°。
我们假设原横纵坐标为 t,p;
可使用矩阵乘法进行旋转:
[ x y ] = [ 1 1 1 − 1 ] [ t p ]
即:
{ x = t + p y = t − p \left\{
写在程序中可以直接写成:
int x,y;
scanf("%d%d",&x,&y);
x += y;
y = x - y * 2;
这样旋转之后,所有 斜率为 1 的直线都是平行于 x 轴的直线,所有斜率为 - 1 的直线都是品性与 y 轴的直线。
(其实仔细思考一下,如果学生向负方向跑步那么他所有出现点,时间和位置的加和不变,如果向正方向跑,其时间和位置的差不变)
下面我们可以建立一个二分图,左边是横坐标,右边是纵坐标。对于点 (xi,yi),我们将 xi 和 yi 连一条边。
接着,如果我们选择一个左边的点 xi 即等于选择了一条直线 x=xi ,同理右边的点 yi 代表着直线 y=yi 。对于没跳变,都要满足它的端点中存在至少一个被选择的点。
下面的问题就转化成了求二分图的最小点覆盖问题,有一个结论:二分图的最小点覆盖等于二分图的最大匹配。 于是转而求这张图的最大匹配即可。
由于题目中的点数量级是 105 使用匈牙利增广路算法 O (n2) 复杂度妥妥超时。于是可以考虑使用最大流来解决这个问题。
使用 dinic 算法跑最大流复杂度是 O (Nsqrt (N))
代码:
#include<iostream>
#include<queue>
#include<cstring>
#include<cstdio>
#include<map>
using namespace std;
const int N = 1e6 + 50;
const int M = 3e6 + 50;
const int inf = 1 << 30;
struct Edge{
int point;
int next;
int flow;
}nxt[N];
int head[N];
int dis[N];
bool vis[N];
int n,T,m1,m2,tot;
int s,t;
map<long long,int> mp1;
map<long long,int> mp2;
queue<int> q;
inline int getMap1(int x){return mp1.find(x)->second;}
inline int getMap2(int x){return mp2.find(x)->second;}
inline int min(int x,int y){return x < y ? x : y;}
bool bfs(){
memset(vis,false,sizeof(vis));
dis[s] = 0;
vis[s] = true;
q.push(s);
int k;
while(!q.empty()){
k = q.front();
q.pop();
for(int i = head[k];i;i = nxt[i].next){
if(vis[nxt[i].point] || !nxt[i].flow)
continue;
dis[nxt[i].point] = dis[k] + 1;
vis[nxt[i].point] = true;
q.push(nxt[i].point);
}
}
return vis[t];
}
int dfs(int k,int flow){
if(k == t || flow == 0){
return flow;
}
int sum = 0,f;
for(int i = head[k];i;i = nxt[i].next){
if(dis[nxt[i].point] == dis[k] + 1 && (f = dfs(nxt[i].point,min(nxt[i].flow,flow)))){
flow -= f;
sum += f;
nxt[i].flow -= f;
nxt[i ^ 1].flow += f;
}
if(!flow)
break;
}
return sum;
}
/*dinic算法*/
int dinic(){
int sum = 0;
while(bfs()){
sum += dfs(s,inf);
}
return sum;
}
void link(int x,int y,int f){
nxt[++tot] = {y,head[x],f};head[x] = tot;
nxt[++tot] = {x,head[y],0};head[y] = tot;
}
int main(){
for(cin >> T;T;T--){
scanf("%d",&n);
m1 = 1;
m2 = n + 10;
mp1.clear();
mp2.clear();
tot = 1;
s = 0;
t = 1;
/*建边的时候建议使用map映射一下x和y的值,它们是离散的,有负数且会很大,不方便处理*/
long long x,y;
while(n--){
scanf("%lld%lld",&x,&y);
x += y;
y = x - y * 2;
if(!mp1.count(x)){
mp1.insert(pair<long long,int>(x,++m1));
link(s,m1,1);
}
if(!mp2.count(y)){
mp2.insert(pair<long long,int>(y,++m2));
link(m2,t,1);
}
link(getMap1(x),getMap2(y),1);
}
cout << dinic() << endl;
for(int i = 0;i <= m2;i++) head[i] = 0;
}
}

AC 的故事大结局山寨版(下)(网络流之最大流,当前弧优化的 dinic)
福建工程学院第十二届 ACM 程序设计大赛真题
AC 的故事大结局山寨版(下)
TimeLimit:2000MS MemoryLimit:128MB64-bit integer IO format: %lld已解决 | 点击收藏Problem Description小 A 算出幕后黑手的人员是如此之多,知道在我们华夏,手段通天者必然身居高位,仅仅靠他们的力量恐怕难以和他们对抗。
于是小 A 和小 C 找到了以前认识的检察官侯亮平,告诉侯亮平事情的始末后,他们立马通知赵东来安排了人手准备逮捕嫌疑人祁同伟(这么大的事居然没有事先向上级汇报就擅自行动)。
现在警厅里只有 P<=100 个警察,F<=100 辆警车和 C<=100 把武器,每辆车和每把武器都有自己的特点,每个警察只会用其中的一些警车和武器。
每辆警车只坐一名警察(不知道为何要这么浪费资源,可能市局比较有钱),每位警察必须带上自己熟练的武器才能驾车出击。
为了打败幕后黑手祁同伟,小 A 合理安排后派出了最多的人手,相信你也一定知道派出了多少警察。最终成功逮捕了嫌疑人祁同伟。
从此小 A 和小 C 过上了幸福快乐的日子。可喜可贺,可喜可贺。
Input先输入一个整数 t(<=100)表示有多少组数据
每组输入 3 个整数 P,F,C,(3 个数都不超过 100) 分别表示警察人数,警车数量和武器数量。
接着第 i 行表示第 i 个警察的能力(共 P 行)。该行先输入两个整数 x,y 表示该警察会驾驶 x 辆汽车和 y 把武器,之后有 x 个整数表示警车的编号和 y 个整数表示武器的编号。
(警车编号:1~F,武器编号:1~C)
Output每组输出一个整数,代表能带上武器驾车出击的警察最多有多少个
SampleInput1 4 3 3 2 2 1 2 3 1 2 2 2 3 1 2 2 2 1 3 1 2 2 1 1 3 3SampleOutput3
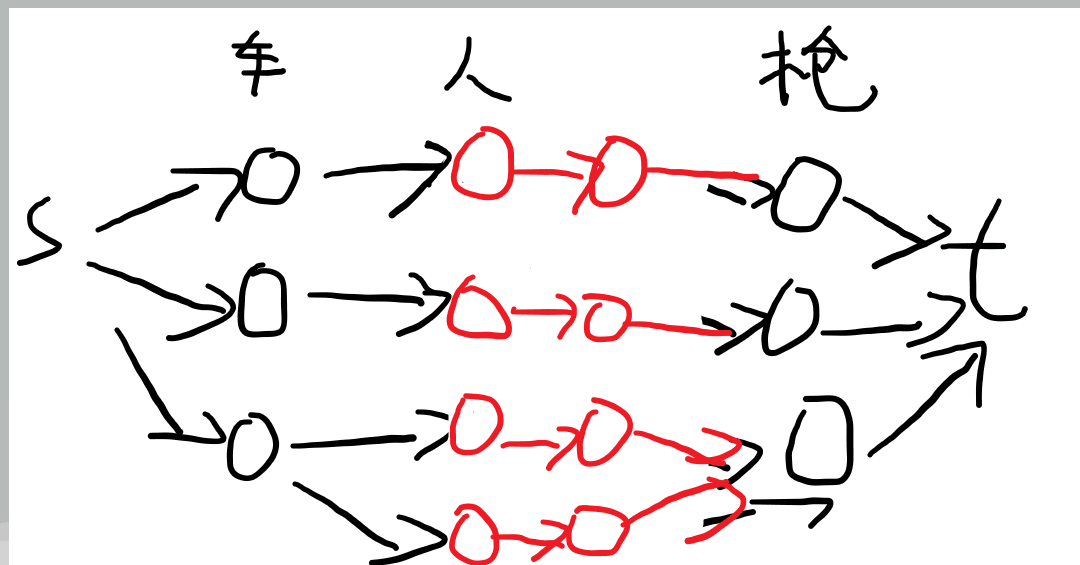
思路:警察,武器,车都看作点,虚拟出源点汇点。保证源点到汇点必须经过一个警察,一个武器,一辆车。另外,警察要拆成两个点,为了避免警察被使用多次。所有关系作为流为 1 的边
正确的图:
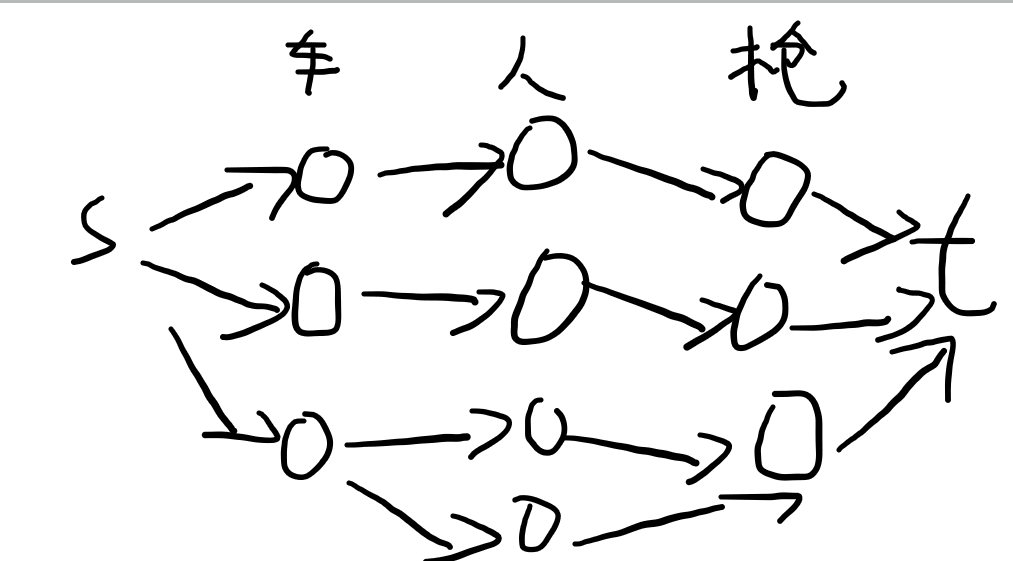
错误的图:
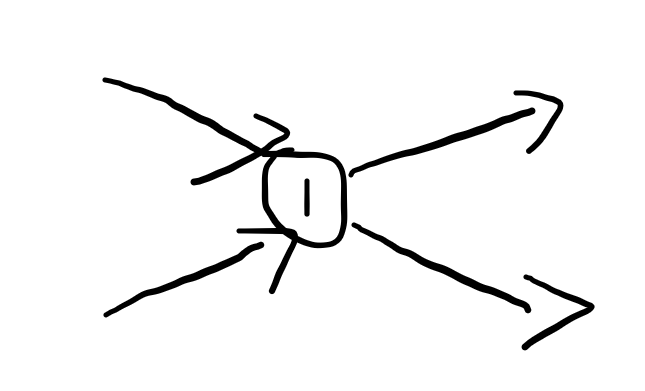
如果有一个人可以使用多个武器多辆车,那么该警察可能被使用多次。如下图,警察 1 就会贡献流量 2。
1 #include <bits/stdc++.h>
2
3 using namespace std;
4 const int MAXN = 1001;
5 const int MAXM = 1e4 + 7;
6 const int INF = 0x7fffffff;
7 typedef long long LL;
8
9 int s, t, p, f, c;
10
11 struct Edge {
12 int to, w, next;
13 } edge[MAXM * 4];
14
15 int first[MAXN], cur[MAXN], sign, dist[MAXN];
16
17 inline void init() {
18 for(int i = 0; i < MAXN; i ++ ) {
19 first[i] = -1;
20 }
21 sign = 0;
22 }
23
24 inline void add_edge(int u,int v,int w) {
25 edge[sign].to = v, edge[sign].w = w;
26 edge[sign].next = first[u], first[u] = sign++;
27 edge[sign].to = u, edge[sign].w = 0;
28 edge[sign].next = first[v], first[v] = sign++;
29 }
30
31 bool bfs(int s,int t) {
32 memset(dist, -1, sizeof(dist));
33 queue<int>que;
34 que.push(s), dist[s] = 0;
35 while(!que.empty()) {
36 int now = que.front();
37 que.pop();
38 if(now == t) {
39 return 1;
40 }
41 for(int i = first[now]; ~i; i = edge[i].next) {
42 int to = edge[i].to, ww = edge[i].w;
43 if(dist[to] == -1 && ww > 0) {
44 dist[to] = dist[now] + 1;
45 que.push(to);
46 }
47 }
48 }
49 return 0;
50 }
51
52 int dfs(int s, int t, int max_flow) {
53 if(s == t) {
54 return max_flow;
55 }
56 for(int &i = cur[s]; ~i; i = edge[i].next) {
57 int to = edge[i].to, ww = edge[i].w;
58 if(dist[to] == dist[s] + 1 && ww > 0) {
59 int flow = dfs(to, t, min(max_flow, ww));
60 if(flow > 0) {
61 edge[i].w -= flow;
62 edge[i ^ 1].w += flow;
63 return flow;
64 }
65 }
66 }
67 return 0;
68 }
69
70 int dinic(int s, int t) {
71 int ans = 0;
72 while(bfs(s, t)) {
73 for(int i = 0; i < MAXN; i ++ ) {
74 cur[i] = first[i];
75 }
76 ans += dfs(s, t, INF);
77 }
78 return ans;
79 }
80
81 template<class T>
82 inline bool nextInt(T &n)
83 {
84 T x = 0, tmp = 1; char c = getchar();
85 while((c < ''0'' || c > ''9'') && c != ''-'' && c != EOF) c = getchar();
86 if(c == EOF) return false;
87 if(c == ''-'') c = getchar(), tmp = -1;
88 while(c >= ''0'' && c <= ''9'') x *= 10, x += (c - ''0''),c = getchar();
89 n = x*tmp;
90 return true;
91 }
92
93 template<class T>
94 inline void out(T n)
95 {
96 if(n < 0)
97 {
98 putchar(''-'');
99 n = -n;
100 }
101 int len = 0,data[20];
102 while(n)
103 {
104 data[len++] = n%10;
105 n /= 10;
106 }
107 if(!len) data[len++] = 0;
108 while(len--) putchar(data[len]+48);
109 }
110
111 int main() {
112 int T;
113 nextInt(T);
114 while(T--) {
115 nextInt(p), nextInt(f), nextInt(c);
116 s = 0, t = 1000;
117 init();
118 for(int i = 1; i <= f; i++ ) { ///s->car
119 add_edge(s, i, 1);
120 }
121 for(int i = 1; i <= p; i++ ) { ///line
122 add_edge(i + 200, i + 400, 1);
123 }
124 for(int i = 1; i <= c; i++ ) { ///gun->t
125 add_edge(i + 600, t, 1);
126 }
127 for(int i = 1; i <= p; i++ ) {
128 int x, y, id;
129 nextInt(x), nextInt(y);
130 for(int j = 1; j <= x; j++ ) { ///car
131 nextInt(id);
132 add_edge(id, i + 200, 1);
133 }
134 for(int j = 1; j <= y; j++ ) { ///gun
135 nextInt(id);
136 add_edge(i + 400, id + 600, 1);
137 }
138 }
139 out(dinic(s, t)), putchar(''\n'');
140 }
141
142 return 0;
143 }

ACM-ICPC Beijing 2016 Genius ACM(倍增 + 二分)
描述
给定一个整数 M,对于任意一个整数集合 S,定义 “校验值” 如下:
从集合 S 中取出 M 对数 (即 2∗M 个数,不能重复使用集合中的数,如果 S 中的整 数不够 M 对,则取到不能取为止),使得 “每对数的差的平方” 之和最大,这个最大值 就称为集合 S 的 “校验值”。
现在给定一个长度为 N 的数列 A 以及一个整数 T。我们要把 A 分成若干段,使得 每一段的 “校验值” 都不超过 T。求最少需要分成几段。
Advanced CPU Manufacturer (ACM) is one of the best CPU manufacturer in the world. Every day, they manufacture n CPU chips and sell them all over the world.
As you may know, each batch of CPU chips must pass a quality test by the QC department before they can be sold. The testing procedure is as follows:
1) Randomly pick m pairs of CPU chips from the batch of chips (If there are less than 2m CPU chips in the batch of chips, pick as many pairs as possible.)
2) For each pair, measure the Relative Performance Difference (RPD) between the two CPU chips. Let Di be the RPD of the i-th pair
3) Calculate the Sqared Performance Difference (SPD) of the batch according to the following formula:
SPD=∑Di2
If there are only 1 CPU in a batch, then the SPD of that batch is 0.
4) The batch of chips pass the test if and only if SPD≤k, where k is a preseted constant
Usually they send all the n CPU chips as a single batch to the QC department every day. As one of the best CPU manufacturer in the world, ACM never fail the test. However, with the continuous improvement of CPU performance, they find that they are at risk!
Of course they don''t want to take any risks. So they make a decision to divide the n chips into several batches to ensure all of them pass the test. What’s more, each batch should be a continuous subsequence of their productions, otherwise the QC department will notice that they are cheating. Quality tests need time and money, so they want to minimize the number of batches.
Given the absolute performance of the n chips P1 ... Pn mesured by ACM in order of manufacture, your task is to determine the minimum number of batches to ensure that all chips pass the test. The RPD of two CPU chips equals to the difference of their absolute performance.
输入格式
The first line contains a single integer T, indicating the number of test cases.
In each test case, the first line contains three integers n, m, k. The second line contains n integers, P1 ... Pn.
输出格式
For each test case, print the answer in a single line.
样例输入
2
5 1 49
8 2 1 7 9
5 1 64
8 2 1 7 9样例输出
2
1数据范围与约定
- T≤12
- 1≤n,m≤5e5
- 0≤k≤1e18
- 0≤Pi≤2e20
思路:
我们知道 max(sum) = (最大 - 最小)²+(次大 - 次小)²+....
①暴力枚举,枚举每个 sum <= T 的最大位置, Σ(ilogi) ≈ O(n²logn)
②二分 如果每次都只是向右扩展一位,那么二分的复杂度将会比枚举要高 O(n²log²n)
③倍增 + 二分 我们让其快速增长,过头后,快速下降。 (倍增 + 二分 logn、排序校验 nlogn) O(nlog²n)
我们让 L = R = P = 1,先校验【L,R+P】,然后倍增 R=R+P,P*=2;不符合要求就 P/=2,直至 P=0,L=R,就是 sum <= T 最大位置
那么每次符合倍增的时候【L,R】是上次校验过的,也就是说是有序的,我们只需要【R,R+P】排序,和前一段合并成【L,R+P】。
这样的复杂度是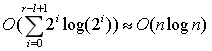


1 #include<bits/stdc++.h>
2 using namespace std;
3
4 const int maxn = 5e5+5;
5 int t;
6 int n,m;
7 int L,R,p;
8
9 typedef long long ll;
10 ll k;
11 ll num[maxn];
12 ll tmpnum[maxn];
13 ll tmpnum2[maxn];
14 void Mergesort(int l,int mid,int r)
15 {
16 int i=l,j=mid+1;
17 int k = l;
18 while(i <= mid && j <= r)
19 {
20 if(tmpnum2[i]<tmpnum2[j])
21 tmpnum[k++] = tmpnum2[i++];
22 else
23 tmpnum[k++] = tmpnum2[j++];
24 }
25 while(i <= mid)
26 tmpnum[k++] = tmpnum2[i++];
27 while(j <= r)
28 tmpnum[k++] = tmpnum2[j++];
29 }
30
31
32 bool Merge(int l,int mid,int r,int p)
33 {
34 for(int i=l; i<=r; i++)
35 tmpnum2[i] = num[i];
36 sort(tmpnum2+mid+1,tmpnum2+r+1);
37 Mergesort(l,mid,r);
38 int len = (l+r)/2;
39 ll tmp = 0;
40 for(int i=l; i<=len&&i < l+m; i++)
41 {
42 tmp += (tmpnum[l+r-i] - tmpnum[i])*(tmpnum[l+r-i] - tmpnum[i]);
43 }
44 if(tmp > k)
45 return 1;
46 else
47 {
48 for(int i=l; i<=r; i++)
49 {
50 num[i] = tmpnum[i];
51 }
52 return 0;
53 }
54 }
55
56 int main()
57 {
58 scanf("%d",&t);
59 while(t--)
60 {
61 scanf("%d%d%lld",&n,&m,&k);
62 for(int i=1; i<=n; i++)
63 scanf("%lld",&num[i]);
64 p=1,R=1,L=1;
65 int sum = 0;
66 while(R <= n)
67 {
68 if(p)
69 {
70 if(R+p > n || Merge(L,R,R+p,p))
71 p/=2;
72 else
73 R+=p,p *= 2;
74 }
75 else
76 {
77 R++;
78 L=R;
79 p++;
80 sum++;
81 }
82 }
83 printf("%d\n",sum);
84 }
85 }
关于POJ-3436:ACM Computer Factory 和Dinic 最大流的介绍已经告一段落,感谢您的耐心阅读,如果想了解更多关于18.10.29 POJ 3987 Computer Virus on Planet Pandora(AC自动机+字符串处理)、2020 杭电多校第四场 1007 Go Running Dinic 最大流跑二分图匹配、AC 的故事大结局山寨版(下)(网络流之最大流,当前弧优化的 dinic)、ACM-ICPC Beijing 2016 Genius ACM(倍增 + 二分)的相关信息,请在本站寻找。
本文标签:





