本文将带您了解关于c–可以boost:algorithm::join()连接一个float的容器?的新内容,同时我们还将为您解释c++链接的相关知识,另外,我们还将为您提供关于AdaboostAlgo
本文将带您了解关于c – 可以boost:algorithm :: join()连接一个float的容器?的新内容,同时我们还将为您解释c++ 链接的相关知识,另外,我们还将为您提供关于Adaboost Algorithm Step、AdaBoost Meta-algorithm 笔记、Algorithm - Network Flow、Algorithm - Network Flow 复习的实用信息。
本文目录一览:- c – 可以boost:algorithm :: join()连接一个float的容器?(c++ 链接)
- Adaboost Algorithm Step
- AdaBoost Meta-algorithm 笔记
- Algorithm - Network Flow
- Algorithm - Network Flow 复习

c – 可以boost:algorithm :: join()连接一个float的容器?(c++ 链接)
我的STL技能很弱.我想知道是否有一个数字容器(float,double,ints)使用相同的功能?似乎应该有一双或者两衬以适应其他类型.
还有stl的复制功能,在这里找到一个很好的例子:
How to print out the contents of a vector?
但是我不喜欢在每个元素之后添加分隔符字符串.我只想使用boost.
谢谢.
解决方法
boost::adaptors::transformed将双精度转换为字符串,然后将它们加在一起. #include <iostream>#include <vector>#include <string>#include <boost/algorithm/string/join.hpp>#include <boost/range/adaptor/transformed.hpp>int main(){ using boost::adaptors::transformed; using boost::algorithm::join; std::vector<double> v{1.1,2.2,3.3,4.4}; std::cout << join( v | transformed( static_cast<std::string(*)(double)>(std::to_string) ),"," );} 输出:
1.100000,2.200000,3.300000,4.400000

Adaboost Algorithm Step
Adaboost Algorithm Step
- 给定一个数据集:
$$ D=\{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}) … (x^{(n)}, y^{(n)})\} $$
并为数据集初始化一个对应的权重分布$W_{k,i}$,得:
$$W_{k,i} = (w_{k,1}, w_{k,2} … w_{k,n})$$
初始时设置$k=1$,且初始时权重向量中的每一项的值为$w_{1i}=\frac{1}{n}, i=1,2…n$
- 对具有权重分布的数据集$D$进行学习,得到基本分类器,记为 $G_k(x):X \to \{-1,1\}$
并且标记此次基本分类器的预测结果为$G_k(x^{(i)}), i\in (1,2…n)$,仍然初始时$k=1$
- 计算基本分类器对应的误差$e_k$ :
$$ e_k = \sum_{i=1}^nw_{k,i}I(G_k(x^{(i)})\neq y^{(i)}) $$
然后根据误差计算基本分类器的 $G_k(x)$ 的权重值 $\alpha_k$ :
$$\alpha_k = \frac{1}{2}log(\frac{1-e_k}{e_k})$$
- 根据第$k$轮的基本分类器$G_k(x)$的权重值更新第$k+1$轮的数据集权重$W_{k+1,i}$:
$$w_{k+1,i}=\frac{w_k,i}{Z_k}exp(-\alpha_k*y^{(i)}*G_k(x^{(i)})) $$
其中$Z_k$为规范化因子,为的是将权重值映射到区间$(0,1)$
$$where: Z_k = \sum_{i=1}^nw_{k,i}*exp(-\alpha_k*y^{(i)}*G_k(x^{(i)}))$$
- 进行了$K$轮的更新后,得到基本分类器的线性组合
$$f(x) = \sum_{k=1}^K\alpha_k*G_k(x)$$
最终的分类器即为$F(x) = sign(f(x)) = \sum_{k=1}^K\alpha_k*G_k(x)$

AdaBoost Meta-algorithm 笔记
AdaBoost Meta-algorithm(Adaptive Boosting Meta-algorithm, 自适应 boosting 元算法) 属于监督学习算法, 它是迭代算法, 其核心思想是针对同一个训练集训练不同的分类器, 即弱分类器, 然后把这些弱分类器集合起来, 构造一个更强的最终分类器.
| 优点 | 泛化错误率低, 易编码, 可以应用在大部分分类器上, 无参数调整 |
| 缺点 | 对离群点敏感 |
| 适用数据类型 | 数值型, 标称型 |
基础概念
1. bagging
bootstrap aggregating(自举汇聚法), 也称bagging方法, 是从原始数据集选择 S 次后得到 S 个新数据集的一种技术. bagging 方法有以下特征:
(1) 新数据集和原数据集样本数相等
(2) 每个数据集都是通过在原始数据集中随机选择一个样本进行替换得到的
(3) 新数据集中可以有重复的值, 而原始数据集中的某些值在新集合中不再出现
(4) 选一个学习算法应用于 S 个数据集, 可得到 S 个分类器
(5) 分类时, 应用这 S 个分类器进行分类, 选择 S 个分类中最多的类别作为分类结果
2. boosting
boosting 与 bagging 类似, 它们在 S 个数据集上都是使用同一个算法进行分类, 即得到的 S 个分类器的类型是一致的. 两者的不同在于:
(1) boosting 的分类器是通过串行训练获得的, 即新分类器根据已训练出的分类器进行训练
(2) boosting 通过关注被已有分类器错分的数据来获取新分类器
(3) bagging 中的分类器权重是相等的, 而 boosting 中的分类器权重不相等
(4) boosting 每个分类器权重代理的是其对应分类器在上一轮迭代中的成功度
3. 分类器错误率

4. 分类器权重 α

5. 训练集样本权重 D
算法对训练集中的每个样本都赋于一个权重, 这些权重构成向量D. 在训练时, 每次迭代完成后, 都会调速各个样本的权重, 分对的样本权重降低, 分错的样本权重升高. 下图依次为样本正确划分和错误划分后的D的计算式:
正确划分: 错误划分:
错误划分: 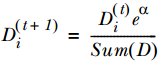
6. sign 函数
符号函数, 用于取某个数的正负号.

算法描述
AdaBoost分为两部分, 对数据集训练出弱分类器和把多个弱分类器集合成强分类器, 以下先给出一个总图, 再分别描述这两个部分.
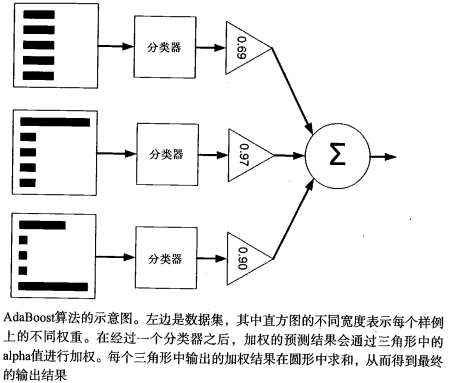
1. 弱分类器训练(本文使用的是单层决策树)
(1) 对样本的每个属性(列), 都按固定步数, 固定步数【(最大值-最小值)/步数】进行划分
(2) 每次划分时, 都把小于当前阈值【步长*当前步数】的划到 -1 类, 大于当前阈值的划到 1 类
(3) 计算加权错误率
(4) 保存权错误率最低时的 dim, thresh, ineq 作为当前决策树的划分规则(代码 62-69行)
2. 弱分类器合并成强分类器
弱分类器的训练是串行进行的, 前面分类器的训练结果会影响后面的分类器
(1) 训练集中的每个样本都赋一个权重, 这些权重合成向量 D;
(2) D 全部初化为 1/m, m为样本数
(3) 以 D 为参数对训练集进行训练, 得到一个弱分类器 (包含最佳划分规则, 最低错误率等)
(4) 根据错误率计算出分类器权重 α, 再根据 α 调整 D
(5) 循环 (3)->(4), 直至最低错误率为 0, 或达到设定的迭代次数
(6) 分类时, 由于每个分类器都有自己的分类结果, 及权重 α, 按以下公式得到新样本所属分类(代码 109-117行)
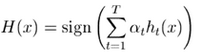
算法流程图
1. 弱分类器训练(本文使用的是单层决策树)

2. 弱分类器合并成强分类器
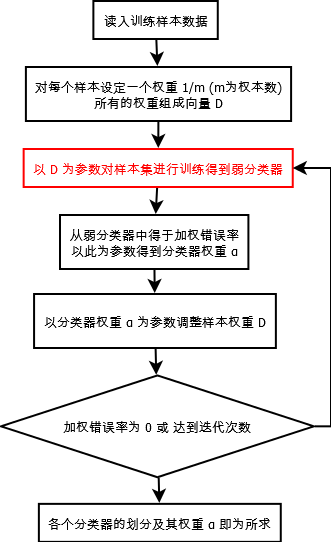
代码
# -*- coding: utf-8 -*
from numpy import *
# 加载简单数据
def loadSimpData():
datMat = matrix([[1. , 2.1],
[2. , 1.1],
[1.3, 1. ],
[1. , 1. ],
[2. , 1. ]])
# 依次表示 datMat 各个点所属分类
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
return datMat,classLabels
# 1. 通过阈值比较对数据分类, 小于阈值的归到 -1 类, 大于阈值的归到 1 类
# 2. lt 表示需要设置的是 less than
# 3. retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 表示:
# 假设 dataMatrix[i, dimen] <= threshVal, 则 retArray[i] = -1
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
# 先全部初始化为 1, 后面只要对需要设置 -1 的部分进行设置即可
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == ''lt'':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray
# 1. 构建单层决策树(因为树只有一层, 所以称为 树桩(stump))
# 2. 本函数将会得到一个弱分类器, 即在当前 D 下, 对哪一列(属性, dim), 什么阈值(thresh),
# 是取大于还是小于(ineq)此阈值时, 能得于最小的加权错误率
# 3. 本文对节点的划分不同于第3章的决策树按最大增益值(熵)来进行,
# 而是基于权重 D, 最小的加权错误率来构建分类器的
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr);
labelMat = mat(classLabels).T # 转置
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
minError = inf # 最小错误率初始化为正无穷
# 遍历所有列, 即所有属性值
for i in range(n):
rangeMin = dataMatrix[:,i].min(); # 取第 i 列的最小值
rangeMax = dataMatrix[:,i].max(); # 取第 i 列的最大值
stepSize = (rangeMax-rangeMin)/numSteps # 计算步长
# 对当前列(属性值), 逐个步长进行遍历
for j in range(-1,int(numSteps)+1):
# 大于和小于当前阈值都要进行考虑
# ''lt'' 表示 less than, ''gt'' 表示 greater than
for inequal in [''lt'', ''gt'']:
threshVal = (rangeMin + float(j) * stepSize) # 当前阈值
# 根据当前阈值划分(按大于/小于), 满足(大于/小于) 的就置为 1
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)
# 与真正类别检签值相一致的设为 1, 不一致的设为 0
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0
# 计算加权错误率, 并保存错误率最小时的 dim, thresh, ineq
weightedError = D.T*errArr #calc total error multiplied by D
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump[''dim''] = i
bestStump[''thresh''] = threshVal
bestStump[''ineq''] = inequal
return bestStump,minError,bestClasEst
# 将多个由 单层决策树(Decision Stump, DS) 弱分类器合并成一个强分类器
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = []
m = shape(dataArr)[0]
# D 初始化为相等的值, 由于D是概率分布向量, 要保证其所有元素和为 1, 所以初始化为 1/m
D = mat(ones((m,1))/m)
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
# 计算 alpha 值
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))
bestStump[''alpha''] = alpha
weakClassArr.append(bestStump) # 保存当前弱分类器的信息
# 按公式计算 D 值, 新的 D 值会被用来进行下一次单层决策树的构建
expon = multiply(-1*alpha*mat(classLabels).T,classEst)
D = multiply(D,exp(expon))
D = D/D.sum()
# 计算总错误率, 当错误率为 0, 或达到循环次数时退出
aggClassEst += alpha*classEst
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
errorRate = aggErrors.sum()/m
if errorRate == 0.0: break
return weakClassArr, aggClassEst
# 分类
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
# 取每个弱分类器的分类结果, 乘以其 alpha 值, 最后相加, 再取 sign 函数
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix,classifierArr[i][''dim''],\
classifierArr[i][''thresh''],\
classifierArr[i][''ineq''])#call stump classify
aggClassEst += classifierArr[i][''alpha'']*classEst
# sign 为符号函数, 即 aggClassEst 为正数, 则返回 1, 否则返回 -1
return sign(aggClassEst)
if __name__ == "__main__":
dataArr, labelArr = loadSimpData()
classifierArr, aggClassEst = adaBoostTrainDS(dataArr, labelArr, 30)
print adaClassify([0, 0],classifierArr) # 分到 -1 类
print adaClassify([2, 2],classifierArr) # 分到 1 类 待补充
1. 非均衡分类问题
说明
本文为《Machine Leaning in Action》第七章(Improving classification with the AdaBoost meta-algorithm)读书笔记, 代码稍作修改及注释.
好文参考
1.《Boosting算法简介》
2.《浅谈Adaboost算法》
3.《理解Adaboost算法》

Algorithm - Network Flow

1. 判断题一道

2. 然后是这道超赞的题

这道题其实分成了好几道小题,其实是在间接引导你解题:
1. 如果告诉你这个 maze (graph) 就是一条直线 O->O->O->...->O,且每条边的 capacity 是 1,请问让所有人员都走出迷宫需要几晚上?
2. 假设现在有个函数 magic(k),能验证所有人能不能用少于 k 晚的时间走出迷宫(返回 boolean value),请问你要怎样利用这个函数去求出所有人到底要用几晚上走出迷宫。
3. 试着自己写出这个 magic(k)函数。
你看,这样一步一步引导下来,你其实就逐渐把这个问题解决了,真的很值得学习呢!
首先看第一步:显然,由于边的 capacity 是 1,每晚只能挪动一个人,所以总时长为 | V|+m-2,不要误以为是 | V|m 哦!
然后第二步:有了 magic(k),而我们在第一步已经知道,k 的可能范围是 <=|V|+m-2 的,所以只需要在 [0, |V|+m-2] 的范围内 binary search 找到能让 magic(k)返回 true 的最大 k 值就 ok 了。
时间复杂度为 O (TC (magic)*log (|V|+m-2)),其中 TC (magic) 为 magic(k)的 time complexity。
然后是第三步,最关键最难的啦,使用 network flow 把 magic (k) 实现:
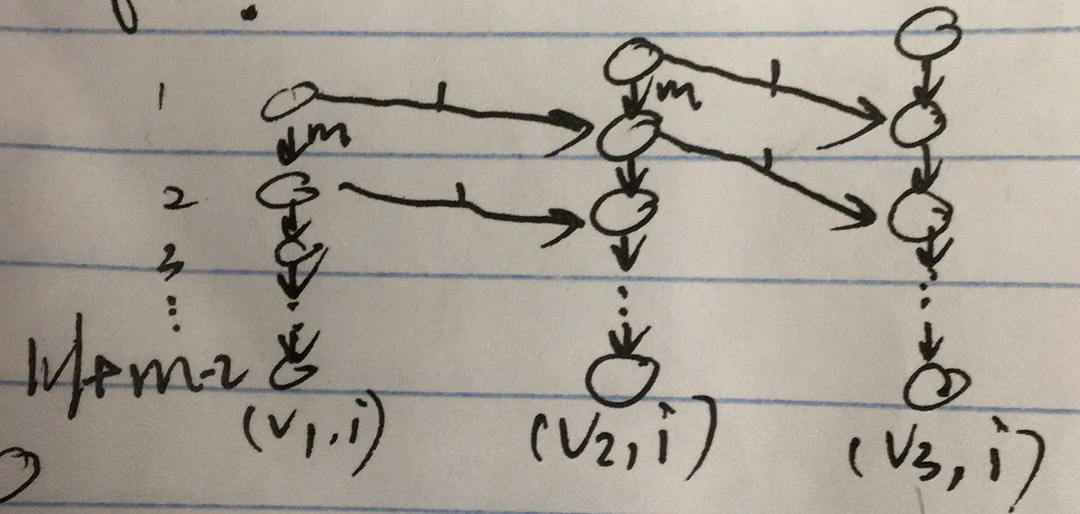
按照这样的方式完成构建 flow network,此时总时间限制为 k 晚。
1. 对每个原图中的 node-v 我们都复制 | V|+m-2 份,记为 (node-v, 1),(node-v, 2),(node-v, 3),...,(node-v, k),并用 capacity 为 m 的边将他们连接起来。
解释:同一个点复制 k 份是代表这个人在这个点停留到了 k 天,因为一共只有最晚会有人在第 k 天走出 graph,所以复制 k 份。而同一个点同时可以容纳的人数没有限制,所以这里的边的 capacity 应该是正无穷,表示第 i 晚呆在点 v 的人,在下一晚可以全部留下来,但因为反正一共才 m 个人,所以我这里就将 capacity 设为了 m。
2. 如果原图中的两 node,比如 n1 和 n2,之间存在边(n1,n2)的话,在这个新建图中就把每个(n1, i)和(n2, i+1)都连接起来,并且将该边的 capacity 设为 1
解释:边 <(n1, i), (n2, i+1)> 表示在第 i 晚可以有一个人从一点走到下一点。
完成这个 flow network 后对这个图进行 fordfulkerson 算法,source 点设为(node-0, 0), sink 点设为(node-n, k),求得 maxflow,如果这个 maxflow 小于人数 m,那就 return false;反之 return true。

Algorithm - Network Flow 复习
network flow 的应用:
1. bipartite matching problem。(employee 和 job 的分配匹配问题)
- 构建 bipartite 图,添加 s,t。
- 看问题中变量的意义,决定图中各边的 capacity。(有点玄学)
- 算 max flow,用 ford-fulkerson 或者别的什么 max flow 算法。
2. minimum cut problem。(image segmentation 问题)
- 利用的是 minimum cut = max flow
--------------------------------------------------------------------------
ford-fulkerson 算法伪码:
Ford-Fulkerson
for <u,v> ∈ E
<u,v>.f = 0
while find a route from s to t in e
m = min(<u,v>.f, <u,v> ∈ route)
for <u,v> ∈ route
if <u,v> ∈ f
<u,v>.f = <u,v>.f + m
else
<v,u>.f = <v,u>.f - m
cut(割)的容量(设 cut<S,T>)= 所有从 S 到 T 的 edge 的 capacity 的和
cut 的 flow = 所有从 S 到 T 的 edge 上的 flow - 所有从 T 到 S 的 edge 上的 flow
如何证明 ford-fulkerson 能得到 max flow?(如何证明没有 augmented path 的时候就达到 max flow 了)
证明:将 residual graph 里所有所有源点 s 能 reach 到的 node 看作集合 S,那么所有 node 的集合 V 减去集合 S 就是集合 T=V-S,T 就是所有源点 s 无法 reach 到的点,此时(S,T)就是一个割。那么对于所有跨 cut<S,T> 的边 < u,v > 必然有 flow(<u,v>)=capacity (<u,v>),不然的话就说明在 residual graph 中 u 有路径可以连接到 v,也就是说源点 s 可以 reach 到 T 中的 v,这和 T 的定义矛盾。
MIT quiz 题:(network flow 是)
https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-design-and-analysis-of-algorithms-spring-2015/exams/MIT6_046JS15_quiz2sols.pdf
我们今天的关于c – 可以boost:algorithm :: join()连接一个float的容器?和c++ 链接的分享就到这里,谢谢您的阅读,如果想了解更多关于Adaboost Algorithm Step、AdaBoost Meta-algorithm 笔记、Algorithm - Network Flow、Algorithm - Network Flow 复习的相关信息,可以在本站进行搜索。
本文标签:





