在本文中,您将会了解到关于sklearnLogistic回归“ValueError:找到的数组具有暗3估计器期望值的新资讯,同时我们还将为您解释找到数组某元素位置的相关在本文中,我们将带你探索skle
在本文中,您将会了解到关于sklearn Logistic回归“ ValueError:找到的数组具有暗3估计器期望值<=2”的新资讯,同时我们还将为您解释找到数组某元素位置的相关在本文中,我们将带你探索sklearn Logistic回归“ ValueError:找到的数组具有暗3估计器期望值<=2”的奥秘,分析找到数组某元素位置的特点,并给出一些关于Deep Learning小白--通过Logistic回归实现神经网络(Andrew Ng)、ImportError:没有名为 sklearn.cross_validation 的模块、JSONDecodeError(“期望值”,s,err.value)、Logistic回归的实用技巧。
本文目录一览:- sklearn Logistic回归“ ValueError:找到的数组具有暗3估计器期望值<=2”(找到数组某元素位置)
- Deep Learning小白--通过Logistic回归实现神经网络(Andrew Ng)
- ImportError:没有名为 sklearn.cross_validation 的模块
- JSONDecodeError(“期望值”,s,err.value)
- Logistic回归

sklearn Logistic回归“ ValueError:找到的数组具有暗3估计器期望值<=2”(找到数组某元素位置)
我尝试在此笔记本中解决此问题6。问题是通过使用来自的LogisticRegression模型,使用50、100、1000和5000个训练样本在此数据上训练简单模型sklearn.linear_model。
lr = LogisticRegression()
lr.fit(train_dataset,train_labels)
这是我尝试执行的代码,它给了我错误。
ValueError:找到的数组为暗3。估计量应小于等于2。
任何想法?
更新1:更新到Jupyter Notebook的链接。

Deep Learning小白--通过Logistic回归实现神经网络(Andrew Ng)
建立一个logstic分类器来识别猫
0.用到的数学公式
$$z^{(i)} = w^T x^{(i)} + b $$
$x^{(i)}$是第i个训练样本
$$\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})$$
$$ \mathcal{L}(a^{(i)}, y^{(i)}) = - y^{(i)} \log(a^{(i)}) - (1-y^{(i)} ) \log(1-a^{(i)})$$
$$ J = \frac{1}{m} \sum_{i=1}^m \mathcal{L}(a^{(i)}, y^{(i)})$$
$J$ 是损失函数,表示预测值与期望输出值的差值
1.导入包
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset #读入数据
%matplotlib inline2.定义σ激活函数
$$sigmoid( w^T x + b) = \frac{1}{1 + e^{-(w^T x + b)}}$$
def sigmoid(z): # z是任何大小的标量或者numpy数组
s = 1 / (1 + np.exp(-z))
return s # s -- sigmoid(z)3.初始化参数
def initialize_with_zeros(dim): # dim - 我们想要的w矢量的大小(或者这种情况下的参数数量)
w = np.zeros((dim, 1))
b = 0
assert(w.shape == (dim, 1))
assert(isinstance(b, float) or isinstance(b, int))
return w, b # w--初始化形状为(dim, 1)的零矩阵 b - 初始化的标量(对应于偏差)4.向前传播和向后传播
$$A = \sigma(w^T X + b) = (a^{(0)}, a^{(1)}, ..., a^{(m-1)}, a^{(m)})$$
$$J = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})$$
$$ \frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T$$
$$ \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})$$
def propagate(w, b, X, Y):
# w -- weights, 一个形状为(num_px * num_px * 3, 1)的numpy数组
# b -- bias, 一个标量
# X -- 形状为(num_px * num_px * 3, number of examples)的数据集
# Y -- 形状为(1, number of examples)的判断标签向量 (图片无猫为0, 有猫为1)
m = X.shape[1]#数据集列数
A = sigmoid(np.dot(w.T,X) + b)
cost = (-1/m)*np.sum(Y * np.log(A) + (1 - Y)*np.log(1-A))
dw = 1/m * np.dot(X, (A - Y).T)
db = 1/m * np.sum(A-Y)
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
grads = {"dw":dw, "db": db}
#cost -- 逻辑回归的负对数似然成本
#dw -- 相对于w的损失梯度, 形状和w一样
#db -- 相对于b的损失梯度, 形状和b一样
return grads, cost5.优化
$$ \theta = \theta - \alpha \text{ } d\theta$$
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
# w -- weights, 一个形状为(num_px * num_px * 3, 1)的numpy数组
# b -- bias, 一个标量
# X -- 形状为(num_px * num_px * 3, number of examples)的数据集
# Y -- 形状为(1, number of examples)的判断标签向量 (图片无猫为0, 有猫为1)
#num_iterations -- 优化循环的迭代次数
#learning_rate -- 梯度下降更新规则的学习率
#print_cost -- 是否打印每100步的损失
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b,X, Y)
dw = grads["dw"]
db = grads["db"]
w = w - learning_rate * dw
b = b - learning_rate * db
if i % 100 == 0:
costs.append(cost)
if print_cost and i % 100 == 0:
print("Cost after iteration %i: %f" %(i, cost))
params = {"w":w, "b":b}
grads = {"dw": dw, "db":db}
#params -- 包含w和b的字典
#grads -- 包含权重和偏差相对于成本函数的梯度的字典
#costs -- 在优化过程中计算的所有成本列表,这将用于绘制学习曲线。
return params, grads, costs6.预测
$$\hat{Y} = A = \sigma(w^T X + b)$$
def predict(w, b, X):
# w -- weights, 一个形状为(num_px * num_px * 3, 1)的numpy数组
# b -- bias, 一个标量
# X -- 形状为(num_px * num_px * 3, number of examples)的数据集
m = X.shape[1]
Y_prediction = np.zeros((1, m))
w = w.reshape(X.shape[0], 1)
A = sigmoid(np.dot(w.T, X) + b)
for i in range(A.shape[1]):
if A[0, i] <= 0.5:
Y_prediction[0, i] = 0
else:
Y_prediction[0, i] = 1
assert(Y_prediction.shape == (1, m))
# Y_prediction -- 包含所有预测(0/1)的numpy数组(向量),用于X中的示例
return Y_prediction7.目标模型
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
''''''
通过调用之前实现的函数来构建逻辑回归模型
变量:
X_train -- 一个形状为(num_px * num_px * 3,m_train)的numpy数组表示的训练集
Y_train -- 形状为(1,m_train)的numpy数组的训练标签(矢量)
X_test -- 一个(num_px * num_px * 3,m_test)的numpy数组形式表示测试集
Y_test -- 由形状(1,m_test)的numpy数组(矢量)表示的测试标签
num_iterations -- 代表迭代次数的超参数来优化参数
learning_rate -- 表示在optimize()的更新规则中使用的学习速率的超参数
print_cost -- 设置为true则以每100次迭代打印成本
返回值:
d -- 包含关于模型的信息的字典。
''''''
# 用零初始化参数
w, b = initialize_with_zeros(X_train.shape[0])
# 梯度下降
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# 从字典“参数”中检索参数w和b
w = parameters["w"]
b = parameters["b"]
# 预测测试/训练集的例子
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
# 打印训练/测试的结果
print("训练准确性: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("测试准确性: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d将数据带入
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)绘制学习曲线(含成本)
costs = np.squeeze(d[''costs''])
plt.plot(costs)
plt.ylabel(''cost'')
plt.xlabel(''iterations (per hundreds)'')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()第一次写,希望大家能提意见

ImportError:没有名为 sklearn.cross_validation 的模块
我在 Ubuntu 14.04 中使用 python 2.7。我使用以下命令安装了 scikit-learn、numpy 和 matplotlib:
sudo apt-get install build-essential python-dev python-numpy \
python-numpy-dev python-scipy libatlas-dev g++ python-matplotlib \
ipython
但是当我导入这些包时:
from sklearn.cross_validation import train_test_split
它返回给我这个错误:
ImportError: No module named sklearn.cross_validation
我需要做什么?

JSONDecodeError(“期望值”,s,err.value)
如何解决JSONDecodeError(“期望值”,s,err.value)?
我收到此错误消息,我真的很困惑。我的错误是:
从None json.decoder.JSONDecodeError引发JSONDecodeError(“期望值”,s,err.value):期望值:第1行第1列(字符0)
这是我的源代码:
import sys
import json
import pandas
from simple_salesforce
import Salesforce,SalesforceLogin,SFType
loginInfo = json.load(open(''login.json''))
username = loginInfo[''username'']
password = loginInfo[''password'']
security_token
= loginInfo[''security_token'']
domain = ''login''
sf = Salesforce(username=username,password=password,security_token=security_token,domain=domain)
解决方法
暂无找到可以解决该程序问题的有效方法,小编努力寻找整理中!
如果你已经找到好的解决方法,欢迎将解决方案带上本链接一起发送给小编。
小编邮箱:dio#foxmail.com (将#修改为@)

Logistic回归
1、介绍
Logistic回归主要用于二分类。属于监督学习算法的一种。
2、过程
1)logistic sigmoid函数
其具体公式为:
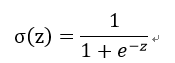
下图给出了其图像:
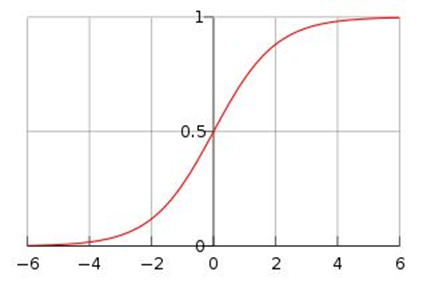
当x为0时,其函数值为0.5,随着x的增大,对应的函数值会逼近于1;随着x的减少,其值会趋于0.当横坐标刻度足够大时,其看上去会像一个阶跃函数。
采用该函数进行回归时,可以在每个特征上乘以一个回归系数,然后把结果相加,总和代入函数中,当函数值大于0.5的被分为1类,否则分为0类。
那么,怎么确定回归系数呢?
假设一个数据含有n个特征值,记为x1,x2,…,xn,对应的回归系数记为w1,w2,w3,…,wn,那么我们可以以矩阵(向量)的形式来表示:
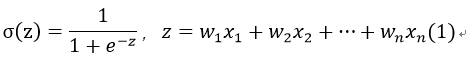
其中:
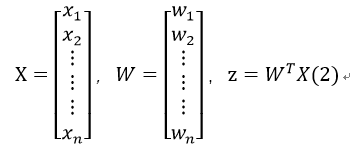
现在我们需要确定W列向量中每个变量的值。
假设有P0和P1两个条件概率:

P0表示在当前W、X的情况下,函数值(我们记为y)为0,即当前数据被分到0类的概率,P1表示被分到1类的概率。
因此我们得到概率函数为:
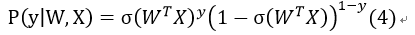
该函数是指,y为1时,就只考虑其为1的概率;y为0时,只考虑为0的概率。我们需要找到合适的W,然后最大化这个概率,尽可能使其分类正确。
2)最佳回归系数确定--基于最优化方法
假定样本与样本之间相互独立,那么整个样本集分类正确的概率即为所有样本分类正确的概率的乘积(似然估计函数),这里我们设总样本数目为m:
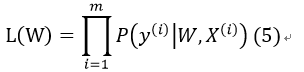
其中,y(i)表示第i个样本的分类,X(i)为第i个样本的特征向量。将式(4)代入式(5),得:
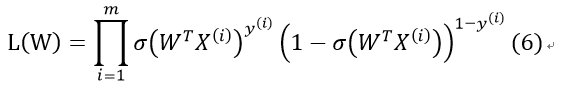
我们通过对该算式取对数ln()进行简化(对数似然函数):
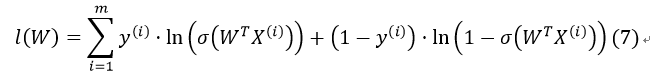
满足该函数最大的W即为我们所要求解的值(最大似然估计值)。
梯度上升法
我们通过用梯度上升法来求其局部极大值(也可以取负对数采用梯度下降法)。即让参数W沿着该函数梯度上升的方向变化:
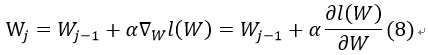
其中,α为步长,即表示向梯度上升方向移动的距离。
对于函数σ(z),其对z的导数为:

接下来,我们对l(W)求偏导:
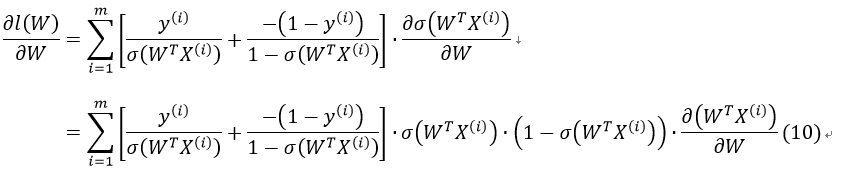
由于:

所以有:
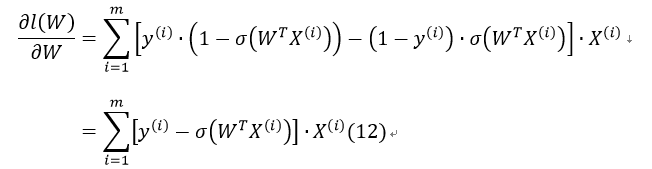
因此,最后梯度上升的迭代公式为:
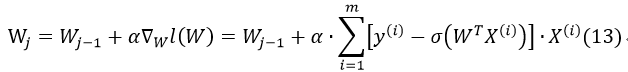
如果把m个样例的特征及其正确分类按行排成矩阵:

其中第i行表示第i个样例的n个特征及其分类。
这样,式13可更改为:

接下来,只需要确定步长α和适宜的迭代次数即可通过X这一训练样本得到符合要求的W,通过W结合logistic sigmoid函数来估计测试数据的分类。
梯度下降法
将对数似然函数乘以一个负系数:

此时可将该式理解为对数损失函数。
此时需要求使得J(W)最小的W值,采用梯度下降法:
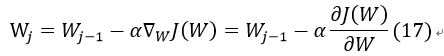
对J(W)求偏导:
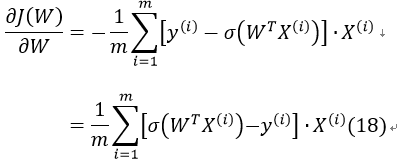
因此式17可改为:
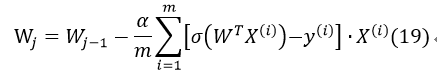
将X,Y改写成矩阵(式14所示),并可将常数1/m省略,则有:
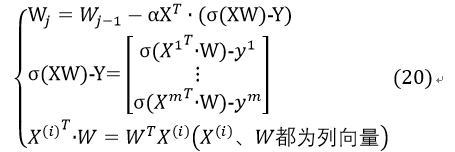
我们今天的关于sklearn Logistic回归“ ValueError:找到的数组具有暗3估计器期望值<=2”和找到数组某元素位置的分享已经告一段落,感谢您的关注,如果您想了解更多关于Deep Learning小白--通过Logistic回归实现神经网络(Andrew Ng)、ImportError:没有名为 sklearn.cross_validation 的模块、JSONDecodeError(“期望值”,s,err.value)、Logistic回归的相关信息,请在本站查询。
本文标签:







