在这里,我们将给大家分享关于剑指Offer的知识,让您更了解Java版:二进制中的1的个数的本质,同时也会涉及到如何更有效地【Java】剑指offer(14)二进制中1的个数、【九度OJ1513】|【
在这里,我们将给大家分享关于剑指Offer的知识,让您更了解Java版:二进制中的1的个数的本质,同时也会涉及到如何更有效地【Java】 剑指offer(14) 二进制中1的个数、【九度OJ1513】|【剑指offer10】二进制中1的个数、【剑指offer】9.二进制中1的个数、【剑指Offer】二进制中1的个数的内容。
本文目录一览:- 剑指Offer(Java版):二进制中的1的个数(java计算二进制中一的个数)
- 【Java】 剑指offer(14) 二进制中1的个数
- 【九度OJ1513】|【剑指offer10】二进制中1的个数
- 【剑指offer】9.二进制中1的个数
- 【剑指Offer】二进制中1的个数

剑指Offer(Java版):二进制中的1的个数(java计算二进制中一的个数)
题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1,因此如果输入9,该函数输出2.
1、可能引起死循环的解法
这是一道很基本的考察二进制和位运算的面试题。题目不是很难,面试官 提出问题之后,我们很快形成一个基本的思路:先判断证书二进制表示中最右边一位是不是1.接着把输入的证书右移一位,此时原来处于从右边树起的第二位被移 到最后一位,再判断是不是1.这样没移动一位,知道整个整数变成0为止。现在的问题变成怎么判断一个整数的最右边是不是1了。这很简单,只要把整数和1做 位与运算看结果是不是0就知道了。1除了最右边的一位之外所有的位都是0.基于这个思路,我们很快写出这样的代码:
package cglib;
public class List1
{
public static int numberOf1(int num) {
int count = 0;
while(num!=0){
if((num&1)!=0)
count++;
num = num>>1;
}
return count;
}
public static void main(String[] args) {
System.out.println(numberOf1(9));
System.out.println(numberOf1(-9));
}
}
只输出了2
负数死循环
面试官看了 代码后可能会问:把证书右移一位和把整数除以2在数学上是等价的,那上面的代码中可以把右移换成除以2吗?答案是否定的。因为除法的效率比移位运算要低很多,在实际编程中应尽可能地用移位运算代替乘除法。
面试官会问第二个问题就是:上面的函数如果输入一个负数,比如 0x80000000,运行的时候会发生什么情况呢?把负数0x80000000右移一位的时候,并不是简单地把最高位的1移到第二位变成 0x40000000,而是0xC0000000.这是因为移位前是个负数,仍然保证移位是个负数,因此移位后的最高位会设为1.如果一直做右移位运算, 最终这个数字会编程0xFFFFFFFF而陷入死循环。
2、常规解法:
为了避免死循环,我们可以不右移输入的数字n.首先把n和1做与运算,判断n的最低位是不是1.接着把1左移一位得到2,再和n做与运算,就能判断n的次低位是不是1。。。。这样反复左移,每次都能判断n的其中一位是不是1.基于这种思路,我们可以写出这样的代码:
package cglib;
public class List1
{
public static int numberOf1(int num) {
int count = 0;
int flag= 1;
while(flag!=0){
if((num&flag)!=0)
count++;
flag =flag <<1;
}
return count;
}
public static void main(String[] args) {
System.out.println(numberOf1(9));
System.out.println(numberOf1(-9));
}
}
输出:
2
31
这个解法中循环的次数等于二进制中的位数,32位的整数需要循环32次,下面我们再介绍一个算法,整数中有几个1就只循环几次。
3、能给面试官带来惊喜的算法。
我们的分析就是:把一个整数减去1,再和原整数做与运算,会把该整数最右边的一个1变成0.那么一个整数的二进制表示中有多少个1,就可以进行多少次运算。基于这种思路,我们可以写出这样的代码:
package cglib;
public class List1
{
public static int numberOf1(int num) {
int count = 0;
while (num != 0) {
count++;
System.out.println("与前:num="+num);//1001
num = num & (num - 1);//00001001&00001000=00001000,00001000&0000111=00000000
System.out.println("与后num="+num);
System.out.println("count="+count);
}
return count;
}
public static void main(String[] args) {
System.out.println(numberOf1(9));
System.out.println(numberOf1(-9));
}
}
输出:
与前:num=9
与后num=8
count=1
与前:num=8
与后num=0
count=2
2
与前:num=-9
与后num=-10
count=1
与前:num=-10
与后num=-12
count=2
与前:num=-12
与后num=-16
count=3
与前:num=-16
与后num=-32
count=4
与前:num=-32
与后num=-64
count=5
与前:num=-64
与后num=-128
count=6
与前:num=-128
与后num=-256
count=7
与前:num=-256
与后num=-512
count=8
与前:num=-512
与后num=-1024
count=9
与前:num=-1024
与后num=-2048
count=10
与前:num=-2048
与后num=-4096
count=11
与前:num=-4096
与后num=-8192
count=12
与前:num=-8192
与后num=-16384
count=13
与前:num=-16384
与后num=-32768
count=14
与前:num=-32768
与后num=-65536
count=15
与前:num=-65536
与后num=-131072
count=16
与前:num=-131072
与后num=-262144
count=17
与前:num=-262144
与后num=-524288
count=18
与前:num=-524288
与后num=-1048576
count=19
与前:num=-1048576
与后num=-2097152
count=20
与前:num=-2097152
与后num=-4194304
count=21
与前:num=-4194304
与后num=-8388608
count=22
与前:num=-8388608
与后num=-16777216
count=23
与前:num=-16777216
与后num=-33554432
count=24
与前:num=-33554432
与后num=-67108864
count=25
与前:num=-67108864
与后num=-134217728
count=26
与前:num=-134217728
与后num=-268435456
count=27
与前:num=-268435456
与后num=-536870912
count=28
与前:num=-536870912
与后num=-1073741824
count=29
与前:num=-1073741824
与后num=-2147483648
count=30
与前:num=-2147483648
与后num=0
count=31
31
扩展1:用一条语句判断一个整数是不是2的整数次方
将2的幂次方写成二进制形式后,很容易就会发现有一个特点:二进制中只有一个1,并且1后面跟了n个0; 因此问题可以转化为判断1后面是否跟了n个0就可以了。
如果将这个数减去1后会发现,仅有的那个1会变为0,而原来的那n个0会变为1;因此将原来的数与去减去1后的数字进行与运算后会发现为零。
最快速的方法:
(number & number - 1) == 0
扩展2:
输 入两个整数m和n,计算需要改变m的二进制表示中的多少位才能得到n。比如10的二进制表示为1010,13的二进制表示为1101,需要改变1010中 的3位才能得到1101 。 我们可以分为两步解决这个问题:第一步求这两个数的异或,第二步统计异或结果中1的位数。
- int GetCount(int N,int M)
- {
- int value=N^M;//先将两个数异或 //0111=7,0110=6
- int count=0;
- while(value)
- {
- count++;
- value=(value&(value-1));//求异或后1的个数 ,0111& 0110 =0110=6;//0101=5,0100=4,
- }
- return count;
- }

【Java】 剑指offer(14) 二进制中1的个数
本文参考自《剑指offer》一书,代码采用Java语言。
更多:《剑指Offer》Java实现合集
题目
请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。
思路
遇到与二进制有关的题目,应该想到位运算(与、或、异或、左移、右移)。
方法一:”与运算“有一个性质:通过与对应位上为1,其余位为0的数进行与运算,可以某一整数指定位上的值。这道题中,先把整数n与1做与运算,判断最低位是否为1;接着把1左移一位,与n做与运算,可以判断次低位是否为1……反复左移,即可对每一个位置都进行判断,从而可以获得1的个数。这种方法需要循环判断32次。
方法二(better):如果一个整数不为0,把这个整数减1,那么原来处在整数最右边的1就会变为0,原来在1后面的所有的0都会变成1。其余所有位将不会受到影响。再把原来的整数和减去1之后的结果做与运算,从原来整数最右边一个1那一位开始所有位都会变成0。因此,把一个整数减1,再和原来的整数做与运算,会把该整数最右边的1变成0。这种方法,整数中有几个1,就只需要循环判断几次。
测试用例
1.正数(包括边界值1、0x7FFFFFFF)
2.负数(包括边界值0x80000000、0xFFFFFFFF)
3.0
完整Java代码
(含测试代码)
/**
*
* @Description 面试题15:二进制中1的个数
*
* @author yongh
* @date 2018年9月17日 下午3:01:16
*/
// 题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如
// 把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。
public class NumberOf1InBinary {
public int NumberOf1_Solution1(int n) {
int count = 0;
int flag = 1;
while (flag != 0) {
if ((flag & n) != 0)
count++;
flag = flag << 1;
}
return count;
}
public int NumberOf1_Solution2(int n) {
int count = 0;
while (n != 0) {
count++;
n = (n - 1) & n;
}
return count;
}
// =========测试代码=========
void test(String testName, int n, int expected) {
if (testName != null)
System.out.println(testName + ":");
if (NumberOf1_Solution1(n) == expected) {
System.out.print(" soluton1:" + "passed ");
} else {
System.out.print(" solution1:" + "failed ");
}
if (NumberOf1_Solution2(n) == expected) {
System.out.println("soluton2:" + "passed ");
} else {
System.out.println("solution2:" + "failed ");
}
}
void test1() {
test("Test for 0", 0, 0);
}
void test2() {
test("Test for 1", 1, 1);
}
void test3() {
test("Test for 10", 10, 2);
}
void test4() {
test("Test for 0x7FFFFFFF", 0x7FFFFFFF, 31);
}
void test5() {
test("Test for 0xFFFFFFFF", 0xFFFFFFFF, 32);
}
void test6() {
test("Test for 0x80000000", 0x80000000, 1);
}
public static void main(String[] args) {
NumberOf1InBinary demo = new NumberOf1InBinary();
demo.test1();
demo.test2();
demo.test3();
demo.test4();
demo.test5();
demo.test6();
}
}


Test for 0:
soluton1:passed soluton2:passed
Test for 1:
soluton1:passed soluton2:passed
Test for 10:
soluton1:passed soluton2:passed
Test for 0x7FFFFFFF:
soluton1:passed soluton2:passed
Test for 0xFFFFFFFF:
soluton1:passed soluton2:passed
Test for 0x80000000:
soluton1:passed soluton2:passed
收获
1.与二进制有关的题目要往位运算方面想,复习一下:二进制位运算的几个用法
2.注意:负数右移还是负数!即如果对n=0x8000 0000右移,最高位的1是不会变的。如果这道题目通过令n=n>>1来计算n中1的个数,该数最终会变成0xFFFF FFFF而陷入死循环!
3.把一个整数减1,再和原来的整数做与运算,会把该整数最右边的1变成0。这种方法一定要牢牢记住,很多情况下都可能用到,例如:
1)一句话判断一个整数是否为2的整数次方;
2)对两个整数m和n,计算需要改变m二进制表示中的几位才能得到n。
4.与数字操作有关的题目,测试时注意边界值的问题。对于32位数字,其正数的边界值为1、0x7FFFFFFF,负数的边界值为0x80000000、0xFFFFFFFF。
5.几个细节问题
1)flag=flag<<1,而不是只写一句flag<<1;
2)flag&n!=0,而非flag&n==1; 也就不能写成count+=(flag&1)了
3)if语句中,不能写为if(flag&n!=0) ,而要写成 if((flag&n)!=0),需要注意一下
更多:《剑指Offer》Java实现合集

【九度OJ1513】|【剑指offer10】二进制中1的个数
题目描述:输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
输入: 输入可能包含多个测试样例。
对于每个输入文件,第一行输入一个整数T,代表测试样例的数量。对于每个测试样例输入为一个整数。
。n保证是int范围内的一个整数。
对应每个测试案例,
输出一个整数,代表输入的那个数中1的个数。
知识点:
- 正数的补码为它本身
- 负数的补码求法
- 补码 = 反码+1(比如:-1 补码:1111 1111 = 1111 1110 + 1);
- 补码 = 模-负数的绝对值(比如:-1 补码:1111 1111(10000 0000 -1得来));
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
/**
* 二进制中1的个数
* @author aqia358
*
*/
public class Main {
public static void count(int t) {
if (t >> 31 == 0) {
System.out.println(num(t));
}else{
long a = 1;
int b = (int)(a << 32) + t;
System.out.println(num(b));
}
}
public static int num(int t) {
int count = 0;
int n = 0;
while (n < 32) {
n++;
if ((t & 1) != 0) {
count++;
}
t >>= 1;
}
return count;
}
public static void main(String[] args) throws IOException {
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
while(st.nextToken() != st.TT_EOF){
int n = (int) st.nval;
while(n > 0){
n -- ;
st.nextToken();
count((int) st.nval);
}
}
}
}

【剑指offer】9.二进制中1的个数
题目
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
分析
这是一道考察二进制的题目
二进制或运算符(or):符号为|,表示若两个二进制位都为0,则结果为0,否则为1。
二进制与运算符(and):符号为&,表示若两个二进制位都为1,则结果为1,否则为0。
二进制否运算符(not):符号为~,表示对一个二进制位取反。
异或运算符(xor):符号为^,表示若两个二进制位不相同,则结果为1,否则为0
左移运算符m << n 表示把m左移n位,左移n位的时候,最左边的n位将被丢弃,同时在最右边补上n个0,比如:
00001010<<2 = 00101000右移运算符m >> n 表示把m右移n位,右移n位的时候,最右边的n位将被丢弃,同时在最左边补上n个0,比如:
00001010>>2 = 00000010我们可以让目标数字和一个数字做与运算
这个用户比较的数字必须只有一位是1其他位是0,这样就可以知道目标数字的这一位是否为0。
所以用于比较的这个数字初始值为1,比较完后让1左移1位,这样就可以依次比较所有位是否为1。
代码
function NumberOf1(n)
{
let flag = 1;
let count = 0;
while(flag){
if(flag & n){
count++;
}
flag = flag << 1;
}
return count;
}
【剑指Offer】二进制中1的个数
题目描述
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
补码
解题前,我们先来了解一下补码。在计算机系统中,数值都是用补码来表示和存储的。 而原码就是数值的二进制数表示,最高位1表示负数。 以32位数值举例 1的原码就是 
-1的原码就是 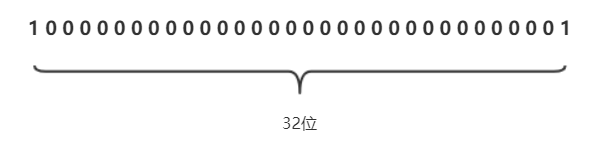
正数的补码等于原码 负数的补码等于其原码按位取反后(除了最高位)加1,比如-1的补码就是32个1 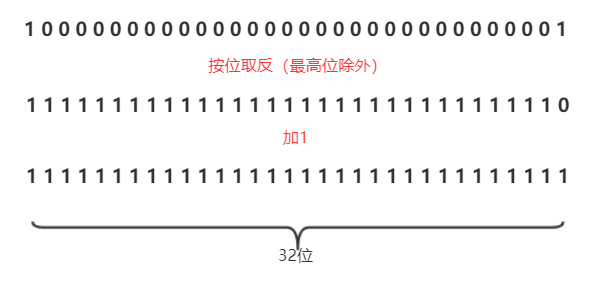
使用补码的好处在于,可以将符号位和数值位统一处理,加法与减法也可以统一处理。 比如3 - 1,等价于3 + (-1),则对于计算机来说将3和-1的补码直接相加就可以,计算过程如下图所示。如果直接使用数值的原码表示,则不会得到正确的结果,感兴趣的同学可以计算试一下,这里不再赘述。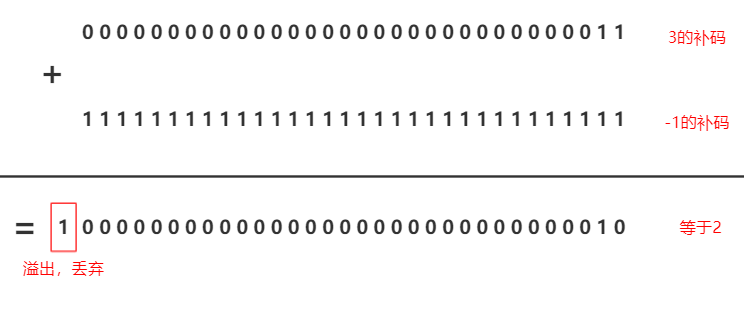
解法1
对于本题,首先想到的是将二进制数一直右移,这样的话该数的每一位都会依次成为最低位,然后将该数和1相与,计算1的个数。(由于1只有最低位是1,其他位都是0,某个数和它相与后,结果如果是1,就说明该数最低位是1,否则就是0) 按照以上思想,实现的代码如下,但是请注意,这样的写法是错误。没有考虑负数的情况,和正数右移最高位补0不同的是,负数右移最高位补1,这样就会有无数个1,导致死循环。
public int NumberOf1(int n)
{
int count = 0;
// 没有考虑负数,一直不会等于0
while(n != 0)
{
if ((n & 1) == 1)
count++;
// 负数右移最高位补1
n >>= 1;
}
return count;
}
既然将目标数右移和1与行不通,那么我们可以反过来,将1不断左移(从最低位到最高位每一位依次是1,其他位是0),然后和目标数相与来求1的个数。具体过程如下图所示 
实现代码
public int NumberOf1(int n)
{
int unit = 1, count = 0;
while (unit != 0)
{
if ((unit & n) != 0)
count++;
unit <<= 1;
}
return count;
}
解法2
上面解法1的时间复杂度是O(n的位数),n有所少位就要循环多少次。可以利用一个小技巧,降低算法的时间复杂度。 先来看一个例子,对于任意一个数将其减1,比如7 7的补码表示是 
(7的补码) 减1后为6,补码表示如下。如果再和7相与,得到的值仍为6。得到的值相当于把7从右边数的第一个1被变成了0 
(6的补码) 比如6,再减1,为5,补码表示如下 
(5的补码) 如果再和6相与,得到的值为4。补码表示如下,得到的值相当于把6从右边数的第一个1被变成了0 
如果用负数进行测试,也是一样的结果。 由此我们可以发现对于数值n,将n - 1后再和n相与,得到的值相当于将n从右边数的第一个1变成0。n的二进制表示中有多少个1,就能变多少次。实现代码如下,时间复杂度优化为O(n中1的个数)
实现代码
public int NumberOf1(int n)
{
int count = 0;
while (n != 0)
{
count++;
n = (n - 1) & n;
}
return count;
}
更多题目的完整描述,AC代码,以及解题思路请参考这里
原文出处:https://www.cnblogs.com/iwiniwin/p/11058255.html
关于剑指Offer和Java版:二进制中的1的个数的问题就给大家分享到这里,感谢你花时间阅读本站内容,更多关于【Java】 剑指offer(14) 二进制中1的个数、【九度OJ1513】|【剑指offer10】二进制中1的个数、【剑指offer】9.二进制中1的个数、【剑指Offer】二进制中1的个数等相关知识的信息别忘了在本站进行查找喔。
本文标签:





