在这篇文章中,我们将带领您了解JS的十大经典算法的全貌,包括js的十大经典算法有哪些的相关情况。同时,我们还将为您介绍有关Go之十大经典排序算法、java十大经典排序算法、java实现十大经典算法、J
在这篇文章中,我们将带领您了解JS的十大经典算法的全貌,包括js的十大经典算法有哪些的相关情况。同时,我们还将为您介绍有关Go 之十大经典排序算法、java 十大经典排序算法、java 实现十大经典算法、JAVA十大经典算法总结的知识,以帮助您更好地理解这个主题。
本文目录一览:
JS的十大经典算法(js的十大经典算法有哪些)
冒泡排序(Bubble Sort)
冒泡排序须知:
作为最简单的排序算法之一,冒泡排序给我的感觉就像Abandon在单词书里出现的感觉一样,每次都在第一页第一位,所以最熟悉。。。冒泡排序还有一种优化算法,就是立一个flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用。。。
什么时候最快(Best Cases):
当输入的数据已经是正序时(都已经是正序了,我还要你冒泡排序有何用啊。。。。)
什么时候最慢(Worst Cases):
当输入的数据是反序时(写一个for循环反序输出数据不就行了,干嘛要用你冒泡排序呢,我是闲的吗。。。)
冒泡排序JavaScript代码实现:
1 function bubbleSort(arr) {
2 var len = arr.length;
3 for (var i = 0; i < len; i++) {
4 for (var j = 0; j < len - 1 - i; j++) {
5 if (arr[j] > arr[j+1]) { //相邻元素两两对比
6 var temp = arr[j+1]; //元素交换
7 arr[j+1] = arr[j];
8 arr[j] = temp;
9 }
10 }
11 }
12 return arr;
13 }选择排序(Selection Sort)
选择排序须知:
在时间复杂度上表现最稳定的排序算法之一,因为无论什么数据进去都是O(n²)的时间复杂度。。。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
选择排序JavaScript代码实现:
1 function selectionSort(arr) {
2 var len = arr.length;
3 var minIndex, temp;
4 for (var i = 0; i < len - 1; i++) {
5 minIndex = i;
6 for (var j = i + 1; j < len; j++) {
7 if (arr[j] < arr[minIndex]) { //寻找最小的数
8 minIndex = j; //将最小数的索引保存
9 }
10 }
11 temp = arr[i];
12 arr[i] = arr[minIndex];
13 arr[minIndex] = temp;
14 }
15 return arr;
16 }插入排序(Insertion Sort)
插入排序须知:
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。当然,如果你说你打扑克牌摸牌的时候从来不按牌的大小整理牌,那估计这辈子你对插入排序的算法都不会产生任何兴趣了。。。
插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。对于这种算法,得了懒癌的我就套用教科书上的一句经典的话吧:感兴趣的同学可以在课后自行研究。。。
插入排序JavaScript代码实现:
1 function insertionSort(arr) {
2 var len = arr.length;
3 var preIndex, current;
4 for (var i = 1; i < len; i++) {
5 preIndex = i - 1;
6 current = arr[i];
7 while(preIndex >= 0 && arr[preIndex] > current) {
8 arr[preIndex+1] = arr[preIndex];
9 preIndex--;
10 }
11 arr[preIndex+1] = current;
12 }
13 return arr;
14 }希尔排序(Shell Sort)
希尔排序须知:
希尔排序是插入排序的一种更高效率的实现。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法(第4版》的合著者Robert Sedgewick提出的。在这里,我就使用了这种方法。
希尔排序JavaScript代码实现:
1 function shellSort(arr) {
2 var len = arr.length,
3 temp,
4 gap = 1;
5 while(gap < len/3) { //动态定义间隔序列
6 gap =gap*3+1;
7 }
8 for (gap; gap> 0; gap = Math.floor(gap/3)) {
9 for (var i = gap; i < len; i++) {
10 temp = arr[i];
11 for (var j = i-gap; j > 0 && arr[j]> temp; j-=gap) {
12 arr[j+gap] = arr[j];
13 }
14 arr[j+gap] = temp;
15 }
16 }
17 return arr;
18 }归并排序(Merge Sort)
归并排序须知:
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
- 自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第2种方法)
- 自下而上的迭代
在《数据结构与算法JavaScript描述》中,作者给出了自下而上的迭代方法。但是对于递归法,作者却认为:
However, it is not possible to do so in JavaScript, as the recursion goes too deep
for the language to handle.
然而,在 JavaScript 中这种方式不太可行,因为这个算法的递归深度对它来讲太深了。
说实话,我不太理解这句话。意思是JavaScript编译器内存太小,递归太深容易造成内存溢出吗?还望有大神能够指教。
更新:
在《JavaScript语言精粹》的第四章里提到了递归问题。对我之前的疑问进行了解答:
Some languages offer the tail recursion optimization. This means that if a function returns the result of invoking itself recursively, then the invocation is replaced with a loop, which can significantly speed things up. Unfortunately, JavaScript does not currently provide tail recursion optimization. Functions that recurse very deeply can fail by exhausting the return stack.
一些语言提供了尾递归优化。这意味着如果一个函数返回自身递归调用的结果,那么调用的过程会被替换为一个循环,它可以显著提高速度。遗憾的是,JavaScript当前并没有提供尾递归优化。深度递归的函数可能会因为堆栈溢出而运行失败。
简而言之,就是JavaScript没有对递归进行优化。运用递归函数不仅没有运行速度上的优势,还可能造成程序运行失败。因此不建议使用递归。
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。
归并排序JavaScript代码实现:
1 function mergeSort(arr) { //采用自上而下的递归方法
2 var len = arr.length;
3 if(len < 2) {
4 return arr;
5 }
6 var middle = Math.floor(len / 2),
7 left = arr.slice(0, middle),
8 right = arr.slice(middle);
9 return merge(mergeSort(left), mergeSort(right));
10 }
11
12 function merge(left, right)
13 {
14 var result = [];
15
16 while (left.length>0 && right.length>0) {
17 if (left[0] <= right[0]) {
18 result.push(left.shift());
19 } else {
20 result.push(right.shift());
21 }
22 }
23
24 while (left.length)
25 result.push(left.shift());
26
27 while (right.length)
28 result.push(right.shift());
29
30 return result;
31 }快速排序(Quick Sort)
快速排序须知:
又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高! 它是处理大数据最快的排序算法之一了。虽然Worst Case的时间复杂度达到了O(n²),但是人家就是优秀,在大多数情况下都比平均时间复杂度为O(n log n) 的排序算法表现要更好,可是这是为什么呢,我也不知道。。。好在我的强迫症又犯了,查了N多资料终于在《算法艺术与信息学竞赛》上找到了满意的答案:
快速排序的最坏运行情况是O(n²),比如说顺序数列的快排。但它的平摊期望时间是O(n log n) ,且O(n log n)记号中隐含的常数因子很小,比复杂度稳定等于O(n log n)的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。
更新:
《算法 第四版》里对于快速排序的优缺点进行了更加明确的解释:
快速排序的内循环比大多数排序算法都要短小,这意味着它无论是在理论上还是在实际中都要更快。它的主要缺点是非常脆弱,在实现时要非常小心才能避免低劣的性能。
快速排序JavaScript代码实现:
1 function quickSort(arr, left, right) { 2 var len = arr.length, 3 partitionIndex, 4 left = typeof left != ''number'' ? 0 : left, 5 right = typeof right != ''number'' ? len - 1 : right; 6 7 if (left < right) { 8 partitionIndex = partition(arr, left, right); 9 quickSort(arr, left, partitionIndex-1); 10 quickSort(arr, partitionIndex+1, right); 11 } 12 return arr; 13 } 14 15 function partition(arr, left ,right) { //分区操作 16 var pivot = left, //设定基准值(pivot) 17 index = pivot + 1; 18 for (var i = index; i <= right; i++) { 19 if (arr[i] < arr[pivot]) { 20 swap(arr, i, index); 21 index++; 22 } 23 } 24 swap(arr, pivot, index - 1); 25 return index-1; 26 } 27 28 function swap(arr, i, j) { 29 var temp = arr[i]; 30 arr[i] = arr[j]; 31 arr[j] = temp; 32 }堆排序(Heap Sort)
堆排序须知:
堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列
堆排序JavaScript代码实现:
1 var len; //因为声明的多个函数都需要数据长度,所以把len设置成为全局变量 2 3 function buildMaxHeap(arr) { //建立大顶堆 4 len = arr.length; 5 for (var i = Math.floor(len/2); i >= 0; i--) { 6 heapify(arr, i); 7 } 8 } 9 10 function heapify(arr, i) { //堆调整 11 var left = 2 * i + 1, 12 right = 2 * i + 2, 13 largest = i; 14 15 if (left < len && arr[left] > arr[largest]) { 16 largest = left; 17 } 18 19 if (right < len && arr[right] > arr[largest]) { 20 largest = right; 21 } 22 23 if (largest != i) { 24 swap(arr, i, largest); 25 heapify(arr, largest); 26 } 27 } 28 29 function swap(arr, i, j) { 30 var temp = arr[i]; 31 arr[i] = arr[j]; 32 arr[j] = temp; 33 } 34 35 function heapSort(arr) { 36 buildMaxHeap(arr); 37 38 for (var i = arr.length-1; i > 0; i--) { 39 swap(arr, 0, i); 40 len--; 41 heapify(arr, 0); 42 } 43 return arr; 44 }计数排序(Counting Sort)
计数排序须知:
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。
作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。计数排序JavaScript代码实现:
1 function countingSort(arr, maxValue) { 2 var bucket = new Array(maxValue+1), 3 sortedIndex = 0; 4 arrLen = arr.length, 5 bucketLen = maxValue + 1; 6 7 for (var i = 0; i < arrLen; i++) { 8 if (!bucket[arr[i]]) { 9 bucket[arr[i]] = 0; 10 } 11 bucket[arr[i]]++; 12 } 13 14 for (var j = 0; j < bucketLen; j++) { 15 while(bucket[j] > 0) { 16 arr[sortedIndex++] = j; 17 bucket[j]--; 18 } 19 } 20 21 return arr; 22 }桶排序(Bucket Sort)
桶排序须知:
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的N个数据均匀的分配到K个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
什么时候最快(Best Cases):
当输入的数据可以均匀的分配到每一个桶中
什么时候最慢(Worst Cases):
当输入的数据被分配到了同一个桶中
桶排序JavaScript代码实现:
1 function bucketSort(arr, bucketSize) { 2 if (arr.length === 0) { 3 return arr; 4 } 5 6 var i; 7 var minValue = arr[0]; 8 var maxValue = arr[0]; 9 for (i = 1; i < arr.length; i++) { 10 if (arr[i] < minValue) { 11 minValue = arr[i]; //输入数据的最小值 12 } else if (arr[i] > maxValue) { 13 maxValue = arr[i]; //输入数据的最大值 14 } 15 } 16 17 //桶的初始化 18 var DEFAULT_BUCKET_SIZE = 5; //设置桶的默认数量为5 19 bucketSize = bucketSize || DEFAULT_BUCKET_SIZE; 20 var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1; 21 var buckets = new Array(bucketCount); 22 for (i = 0; i < buckets.length; i++) { 23 buckets[i] = []; 24 } 25 26 //利用映射函数将数据分配到各个桶中 27 for (i = 0; i < arr.length; i++) { 28 buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]); 29 } 30 31 arr.length = 0; 32 for (i = 0; i < buckets.length; i++) { 33 insertionSort(buckets[i]); //对每个桶进行排序,这里使用了插入排序 34 for (var j = 0; j < buckets[i].length; j++) { 35 arr.push(buckets[i][j]); 36 } 37 } 38 39 return arr; 40 }基数排序(Radix Sort)
基数排序须知:
基数排序有两种方法:
- MSD 从高位开始进行排序
- LSD 从低位开始进行排序
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
基数排序:根据键值的每位数字来分配桶
计数排序:每个桶只存储单一键值
桶排序:每个桶存储一定范围的数值基数排序JavaScript代码实现:
1 //LSD Radix Sort 2 var counter = []; 3 function radixSort(arr, maxDigit) { 4 var mod = 10; 5 var dev = 1; 6 for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) { 7 for(var j = 0; j < arr.length; j++) { 8 var bucket = parseInt((arr[j] % mod) / dev); 9 if(counter[bucket]==null) { 10 counter[bucket] = []; 11 } 12 counter[bucket].push(arr[j]); 13 } 14 var pos = 0; 15 for(var j = 0; j < counter.length; j++) { 16 var value = null; 17 if(counter[j]!=null) { 18 while ((value = counter[j].shift()) != null) { 19 arr[pos++] = value; 20 } 21 } 22 } 23 } 24 return arr; 25 }

Go 之十大经典排序算法
1. 冒泡排序
func bubble_sort(li []int) {
for i := 0; i < len(li)-1; i++ {
exchange := false
for j := 0; j < len(li)-i-1; j++ {
if li[j] > li[j+1] {
li[j], li[j+1] = li[j+1], li[j]
exchange = true
}
}
if !exchange {
return
}
}
}
2. 选择排序
func select_sort(li []int) {
for i := 0; i < len(li)-1; i++ {
pos := i
for j := i + 1; j < len(li); j++ {
if li[pos] > li[j] {
pos = j
}
}
li[i], li[pos] = li[pos], li[i]
}
}
3. 插入排序
func insert_sort(li []int) {
for i := 1; i < len(li); i++ {
tmp := li[i]
j := i - 1
for j >= 0 && tmp < li[j] {
li[j+1] = li[j]
j --
}
li[j+1] = tmp
}
}
4. 希尔排序
func shell_sort(li []int) {
for gap := len(li) / 2; gap > 0; gap /= 2 {
for i := gap; i < len(li); i++ {
tmp := li[i]
j := i - gap
for j >= 0 && tmp < li[j] {
li[j+gap] = li[j]
j -= gap
}
li[j+gap] = tmp
}
}
}
5. 快速排序
func quick_sort(li []int, left, right int) {
if left >= right {
return
}
i := left
j := right
rand.Seed(time.Now().Unix())
r := rand.Intn(right-left) + left
li[i], li[r] = li[r], li[i]
tmp := li[i]
for i < j {
for i < j && li[j] >= tmp {
j--
}
li[i] = li[j]
for i < j && li[i] <= tmp {
i++
}
li[j] = li[i]
}
li[i] = tmp
quick_sort(li, left, i-1)
quick_sort(li, i+1, right)
}
6. 堆排序
func sift(li []int, low, high int) {
i := low
j := 2*i + 1
tmp:=li[i]
for j <= high {
if j < high && li[j] < li[j+1] {
j++
}
if tmp < li[j] {
li[i] = li[j]
i = j
j = 2*i + 1
} else {
break
}
}
li[i] = tmp
}
func heap_sort(li []int) {
for i := len(li)/2 - 1; i >= 0; i-- {
sift(li, i, len(li)-1)
}
for j := len(li) - 1; j > 0; j-- {
li[0], li[j] = li[j], li[0]
sift(li, 0, j-1)
}
}
7. 归并排序
func merge(li []int, left, mid, right int) {
i := left
j := mid + 1
tmp := []int{}
for i <= mid && j <= right {
if li[i] <= li[j] {
tmp = append(tmp, li[i])
i ++
} else {
tmp = append(tmp, li[j])
j ++
}
}
if i <= mid {
tmp = append(tmp, li[i:mid+1]...)
} else {
tmp = append(tmp, li[j:right+1]...)
}
for k := 0; k < len(tmp); k++ {
li[left+k] = tmp[k]
}
}
func merge_sort(li []int, left, right int) {
if left < right {
mid := (left + right) / 2
merge_sort(li, left, mid)
merge_sort(li, mid+1, right)
merge(li, left, mid, right)
}
}
8. 计数排序
func count_sort(li []int) {
max_num := li[0]
for i := 1; i < len(li); i++ {
if max_num < li[i] {
max_num = li[i]
}
}
arr := make([]int, max_num+1)
for j := 0; j < len(li); j++ {
arr[li[j]]++
}
k := 0
for m, n := range arr {
for p := 0; p < n; p++ {
li[k] = m
k++
}
}
}
9. 桶排序
func bin_sort(li []int, bin_num int) {
min_num, max_num := li[0], li[0]
for i := 0; i < len(li); i++ {
if min_num > li[i] {
min_num = li[i]
}
if max_num < li[i] {
max_num = li[i]
}
}
bin := make([][]int, bin_num)
for j := 0; j < len(li); j++ {
n := (li[j] - min_num) / ((max_num - min_num + 1) / bin_num)
bin[n] = append(bin[n], li[j])
k := len(bin[n]) - 2
for k >= 0 && li[j] < bin[n][k] {
bin[n][k+1] = bin[n][k]
k--
}
bin[n][k+1] = li[j]
}
o := 0
for p, q := range bin {
for t := 0; t < len(q); t++ {
li[o] = bin[p][t]
o++
}
}
}
10. 基数排序
func radix_sort(li []int) {
max_num := li[0]
for i := 0; i < len(li); i++ {
if max_num < li[i] {
max_num = li[i]
}
}
for j := 0; j < len(strconv.Itoa(max_num)); j++ {
bin := make([][]int, 10)
for k := 0; k < len(li); k++ {
n := li[k] / int(math.Pow(10, float64(j))) % 10
bin[n] = append(bin[n], li[k])
}
m := 0
for p := 0; p < len(bin); p++ {
for q := 0; q < len(bin[p]); q++ {
li[m] = bin[p][q]
m++
}
}
}
}
11. 用堆排解决 top_k 问题,思路:
a. 先取前 k 个数建小根堆,这样就能保证堆顶元素是整个堆的最小值;
b. 然后遍历列表的 k 到最后,如果值比堆顶大,就和堆顶交换,交换完后再对堆建小根堆,这样就能保证交换完后,堆顶元素仍然是整个堆的最小值;
c. 一直遍历到列表的最后一个值,这一步做完之后,就保证了整个列表最大的前 k 个数已经放进了堆里;
d. 按数的大到小出堆;
func sift(li []int, low, high int) {
i := low
j := 2*i + 1
tmp := li[i]
for j <= high {
if j < high && li[j] > li[j+1] {
j++
}
if tmp > li[j] {
li[i] = li[j]
i = j
j = 2*i + 1
} else {
break
}
}
li[i] = tmp
}
func top_k(li []int, k int) []int {
for i := k/2 - 1; i >= 0; i-- {
sift(li, i, k-1)
}
for j := k; j < len(li); j++ {
if li[0] < li[j] {
li[0], li[j] = li[j], li[0]
sift(li, 0, k-1)
}
}
for n := k - 1; n > 0; n-- {
li[0], li[n] = li[n], li[0]
sift(li, 0, n-1)
}
return li[:k]
}

java 十大经典排序算法
十大排序算法可以说是每个程序员都必须得掌握的了,花了一天的时间把代码实现且整理了一下,为了方便大家学习,我把它整理成一篇文章,每种算法会有简单的算法思想描述,为了方便大家理解,我还找来了动图演示;这还不够,我还附上了对应的优质文章,看完不懂你来砍我,如果不想砍我就给我来个好看。
术语铺垫
有些人可能不知道什么是稳定排序、原地排序、时间复杂度、空间复杂度,我这里先简单解释一下:
1、稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 仍然在 b 的前面,则为稳定排序。
2、非稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 可能不在 b 的前面,则为非稳定排序。
3、原地排序:原地排序就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
4、非原地排序:需要利用额外的数组来辅助排序。
5、时间复杂度:一个算法执行所消耗的时间。
6、空间复杂度:运行完一个算法所需的内存大小。
十大排序讲解顺序
为了方便大家查找,我这里弄一个伪目录,没有跳转功能。
选择排序
插入排序
冒泡排序
非优化版本
优化版本
希尔排序
归并排序
递归式归并排序
非递归式归并排序
快速排序
堆排序
基数排序
非优化版本
优化版本
桶排序
基数排序
另:
代码说明:代码我自己写的,并且都是经过好几组数据测试通过,应该没啥问题,如有错,还请反馈下,谢谢。
图片说明:图片和动画都是在百度搜索的,如有侵权,还望联系我删除,谢谢
1、选择排序
过程简单描述:
首先,找到数组中最小的那个元素,其次,将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。其次,在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此往复,直到将整个数组排序。这种方法我们称之为选择排序。
为方便理解我还准备了动图:
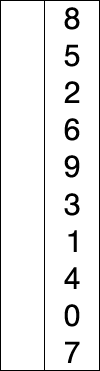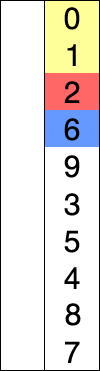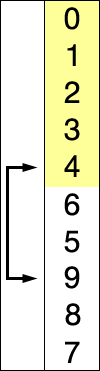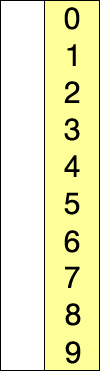
如果还是不懂的话我还给你准备了优质的文章讲解:选择排序
代码如下(代码片可以左右拉动,下同):
1public class SelectSort {
2 public static int[] selectSort(int[] a) {
3 int n = a.length;
4 for (int i = 0; i < n - 1; i++) {
5 int min = i;
6 for (int j = i + 1; j < n; j++) {
7 if(a[min] > a[j]) min = j;
8 }
9 //交换
10 int temp = a[i];
11 a[i] = a[min];
12 a[min] = temp;
13 }
14 return a;
15 }
16}
性质:1、时间复杂度:O(n2) 2、空间复杂度:O(1) 3、非稳定排序 4、原地排序
2、插入排序
我们在玩打牌的时候,你是怎么整理那些牌的呢?一种简单的方法就是一张一张的来,将每一张牌插入到其他已经有序的牌中的适当位置。当我们给无序数组做排序的时候,为了要插入元素,我们需要腾出空间,将其余所有元素在插入之前都向右移动一位,这种算法我们称之为插入排序。
过程简单描述:
1、从数组第2个元素开始抽取元素。
2、把它与左边第一个元素比较,如果左边第一个元素比它大,则继续与左边第二个元素比较下去,直到遇到不比它大的元素,然后插到这个元素的右边。
3、继续选取第3,4,….n个元素,重复步骤 2 ,选择适当的位置插入。
为方便理解我还准备了动图:
如果还是不懂的话我还给你准备了优质的文章讲解:插入排序
代码如下:
1public class InsertSort {
2 public static int[] insertSort(int[] arr) {
3 if(arr == null || arr.length < 2)
4 return arr;
5
6 int n = arr.length;
7 for (int i = 1; i < n; i++) {
8 int temp = arr[i];
9 int k = i - 1;
10 while(k >= 0 && arr[k] > temp)
11 k--;
12 //腾出位置插进去,要插的位置是 k + 1;
13 for(int j = i ; j > k + 1; j--)
14 arr[j] = arr[j-1];
15 //插进去
16 arr[k+1] = temp;
17 }
18 return arr;
19 }
20}
性质:1、时间复杂度:O(n2) 2、空间复杂度:O(1) 3、稳定排序 4、原地排序
3、冒泡排序
1、把第一个元素与第二个元素比较,如果第一个比第二个大,则交换他们的位置。接着继续比较第二个与第三个元素,如果第二个比第三个大,则交换他们的位置….
我们对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样一趟比较交换下来之后,排在最右的元素就会是最大的数。
除去最右的元素,我们对剩余的元素做同样的工作,如此重复下去,直到排序完成。
为方便理解我还准备了动图:

如果还是不懂的话我还给你准备了优质的文章讲解:冒泡排序
代码如下
1public class BubbleSort {
2 public static int[] bubbleSort(int[] arr) {
3 if (arr == null || arr.length < 2) {
4 return arr;
5 }
6 int n = arr.length;
7 for (int i = 0; i < n; i++) {
8 for (int j = 0; j < n -i - 1; j++) {
9 if (arr[j + 1] < arr[j]) {
10 int t = arr[j];
11 arr[j] = arr[j+1];
12 arr[j+1] = t;
13 }
14 }
15 }
16 return arr;
17 }
18)
性质:1、时间复杂度:O(n2) 2、空间复杂度:O(1) 3、稳定排序 4、原地排序
优化一下冒泡排序的算法
假如从开始的第一对到结尾的最后一对,相邻的元素之间都没有发生交换的操作,这意味着右边的元素总是大于等于左边的元素,此时的数组已经是有序的了,我们无需再对剩余的元素重复比较下去了。
代码如下:
1public class BubbleSort {
2 public static int[] bubbleSort(int[] arr) {
3 if (arr == null || arr.length < 2) {
4 return arr;
5 }
6 int n = arr.length;
7 for (int i = 0; i < n; i++) {
8 boolean flag = true;
9 for (int j = 0; j < n -i - 1; j++) {
10 if (arr[j + 1] < arr[j]) {
11 flag = false;
12 int t = arr[j];
13 arr[j] = arr[j+1];
14 arr[j+1] = t;
15 }
16 }
17 //一趟下来是否发生位置交换
18 if(false)
19 break;
20 }
21 return arr;
22 }
23}
4、希尔排序
希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。也就是说,原数组的一个元素如果距离它正确的位置很远的话,则需要与相邻元素交换很多次才能到达正确的位置,这样是相对比较花时间了。
希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序。
希尔排序的思想是采用插入排序的方法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是 h = n / 2,接着让 h = n / 4,让 h 一直缩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。
为方便理解我还准备了图片:
如果还是不懂的话我还给你准备了优质的文章讲解:希尔排序
代码如下
1public class ShellSort {
2 public static int[] shellSort(int arr[]) {
3 if (arr == null || arr.length < 2) return arr;
4 int n = arr.length;
5 // 对每组间隔为 h的分组进行排序,刚开始 h = n / 2;
6 for (int h = n / 2; h > 0; h /= 2) {
7 //对各个局部分组进行插入排序
8 for (int i = h; i < n; i++) {
9 // 将arr[i] 插入到所在分组的正确位置上
10 insertI(arr, h, i);
11 }
12 }
13 return arr;
14 }
15
16 /**
17 * 将arr[i]插入到所在分组的正确位置上
18 * arr[i]] 所在的分组为 ... arr[i-2*h],arr[i-h], arr[i+h] ...
19 */
20 private static void insertI(int[] arr, int h, int i) {
21 int temp = arr[i];
22 int k;
23 for (k = i - h; k > 0 && temp < arr[k]; k -= h) {
24 arr[k + h] = arr[k];
25 }
26 arr[k + h] = temp;
27 }
28}
需要注意的是,对各个分组进行插入的时候并不是先对一个组排序完了再来对另一个组排序,而是轮流对每个组进行排序。
性质:1、时间复杂度:O(nlogn) 2、空间复杂度:O(1) 3、非稳定排序 4、原地排序
5、归并排序
将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很快的。
通过递归的方式将大的数组一直分割,直到数组的大小为 1,此时只有一个元素,那么该数组就是有序的了,之后再把两个数组大小为1的合并成一个大小为2的,再把两个大小为2的合并成4的 ….. 直到全部小的数组合并起来。
为方便理解我还准备了动图:
如果还是不懂的话我还给你准备了优质的文章讲解:归并排序
代码如下:
1public class MergeSort {
2 // 归并排序
3 public static int[] mergeSort(int[] arr, int left, int right) {
4 // 如果 left == right,表示数组只有一个元素,则不用递归排序
5 if (left < right) {
6 // 把大的数组分隔成两个数组
7 int mid = (left + right) / 2;
8 // 对左半部分进行排序
9 arr = mergeSort(arr, left, mid);
10 // 对右半部分进行排序
11 arr = mergeSort(arr, mid + 1, right);
12 //进行合并
13 merge(arr, left, mid, right);
14 }
15 return arr;
16 }
17
18 // 合并函数,把两个有序的数组合并起来
19 // arr[left..mif]表示一个数组,arr[mid+1 .. right]表示一个数组
20 private static void merge(int[] arr, int left, int mid, int right) {
21 //先用一个临时数组把他们合并汇总起来
22 int[] a = new int[right - left + 1];
23 int i = left;
24 int j = mid + 1;
25 int k = 0;
26 while (i <= mid && j <= right) {
27 if (arr[i] < arr[j]) {
28 a[k++] = arr[i++];
29 } else {
30 a[k++] = arr[j++];
31 }
32 }
33 while(i <= mid) a[k++] = arr[i++];
34 while(j <= right) a[k++] = arr[j++];
35 // 把临时数组复制到原数组
36 for (i = 0; i < k; i++) {
37 arr[left++] = a[i];
38 }
39 }
40}
性质:1、时间复杂度:O(nlogn) 2、空间复杂度:O(n) 3、稳定排序 4、非原地排序
然而面试官要你写个非递归式的归并排序怎么办?别怕,我这还撸了个非递归式的归并排序,代码如下:
1public class MergeSort {
2 // 非递归式的归并排序
3 public static int[] mergeSort(int[] arr) {
4 int n = arr.length;
5 // 子数组的大小分别为1,2,4,8...
6 // 刚开始合并的数组大小是1,接着是2,接着4....
7 for (int i = 1; i < n; i += i) {
8 //进行数组进行划分
9 int left = 0;
10 int mid = left + i - 1;
11 int right = mid + i;
12 //进行合并,对数组大小为 i 的数组进行两两合并
13 while (right < n) {
14 // 合并函数和递归式的合并函数一样
15 merge(arr, left, mid, right);
16 left = right + 1;
17 mid = left + i - 1;
18 right = mid + i;
19 }
20 // 还有一些被遗漏的数组没合并,千万别忘了
21 // 因为不可能每个字数组的大小都刚好为 i
22 if (left < n && mid < n) {
23 merge(arr, left, mid, n - 1);
24 }
25 }
26 return arr;
27 }
28}
6、快速排序
我们从数组中选择一个元素,我们把这个元素称之为中轴元素吧,然后把数组中所有小于中轴元素的元素放在其左边,所有大于或等于中轴元素的元素放在其右边,显然,此时中轴元素所处的位置的是有序的。也就是说,我们无需再移动中轴元素的位置。
从中轴元素那里开始把大的数组切割成两个小的数组(两个数组都不包含中轴元素),接着我们通过递归的方式,让中轴元素左边的数组和右边的数组也重复同样的操作,直到数组的大小为1,此时每个元素都处于有序的位置。
为方便理解我还准备了动图:
如果还是不懂的话我还给你准备了优质的文章讲解:不要在问我快速排序
代码如下:
1public class QuickSort {
2 public static int[] quickSort(int[] arr, int left, int right) {
3 if (left < right) {
4 //获取中轴元素所处的位置
5 int mid = partition(arr, left, right);
6 //进行分割
7 arr = quickSort(arr, left, mid - 1);
8 arr = quickSort(arr, mid + 1, right);
9 }
10 return arr;
11 }
12
13 private static int partition(int[] arr, int left, int right) {
14 //选取中轴元素
15 int pivot = arr[left];
16 int i = left + 1;
17 int j = right;
18 while (true) {
19 // 向右找到第一个小于等于 pivot 的元素位置
20 while (i <= j && arr[i] <= pivot) i++;
21 // 向左找到第一个大于等于 pivot 的元素位置
22 while(i <= j && arr[j] >= pivot ) j--;
23 if(i >= j)
24 break;
25 //交换两个元素的位置,使得左边的元素不大于pivot,右边的不小于pivot
26 int temp = arr[i];
27 arr[i] = arr[j];
28 arr[j] = temp;
29 }
30 arr[left] = arr[j];
31 // 使中轴元素处于有序的位置
32 arr[j] = pivot;
33 return j;
34 }
35}
性质:1、时间复杂度:O(nlogn) 2、空间复杂度:O(logn) 3、非稳定排序 4、原地排序
7、堆排序
堆的特点就是堆顶的元素是一个最值,大顶堆的堆顶是最大值,小顶堆则是最小值。
堆排序就是把堆顶的元素与最后一个元素交换,交换之后破坏了堆的特性,我们再把堆中剩余的元素再次构成一个大顶堆,然后再把堆顶元素与最后第二个元素交换….如此往复下去,等到剩余的元素只有一个的时候,此时的数组就是有序的了。
为方便理解我还准备了动图:
如果还是不懂的话我还给你准备了优质的文章讲解:堆排序是什么鬼?
代码如下:
1public class Head {
2 // 堆排序
3 public static int[] headSort(int[] arr) {
4 int n = arr.length;
5 //构建大顶堆
6 for (int i = (n - 2) / 2; i >= 0; i--) {
7 downAdjust(arr, i, n - 1);
8 }
9 //进行堆排序
10 for (int i = n - 1; i >= 1; i--) {
11 // 把堆顶元素与最后一个元素交换
12 int temp = arr[i];
13 arr[i] = arr[0];
14 arr[0] = temp;
15 // 把打乱的堆进行调整,恢复堆的特性
16 downAdjust(arr, 0, i - 1);
17 }
18 return arr;
19 }
20
21 //下沉操作
22 public static void downAdjust(int[] arr, int parent, int n) {
23 //临时保存要下沉的元素
24 int temp = arr[parent];
25 //定位左孩子节点的位置
26 int child = 2 * parent + 1;
27 //开始下沉
28 while (child <= n) {
29 // 如果右孩子节点比左孩子大,则定位到右孩子
30 if(child + 1 <= n && arr[child] < arr[child + 1])
31 child++;
32 // 如果孩子节点小于或等于父节点,则下沉结束
33 if (arr[child] <= temp ) break;
34 // 父节点进行下沉
35 arr[parent] = arr[child];
36 parent = child;
37 child = 2 * parent + 1;
38 }
39 arr[parent] = temp;
40 }
41}
性质:1、时间复杂度:O(nlogn) 2、空间复杂度:O(1) 3、非稳定排序 4、原地排序
8、计数排序
计数排序是一种适合于最大值和最小值的差值不是不是很大的排序。
基本思想:就是把数组元素作为数组的下标,然后用一个临时数组统计该元素出现的次数,例如 temp[i] = m, 表示元素 i 一共出现了 m 次。最后再把临时数组统计的数据从小到大汇总起来,此时汇总起来是数据是有序的。
为方便理解我还准备了动图:

如果还是不懂的话我还给你准备了优质的文章讲解:什么是计数排序?
代码如下:
1public class Counting {
2 public static int[] countSort(int[] arr) {
3 if(arr == null || arr.length < 2) return arr;
4
5 int n = arr.length;
6 int max = arr[0];
7 // 寻找数组的最大值
8 for (int i = 1; i < n; i++) {
9 if(max < arr[i])
10 max = arr[i];
11 }
12 //创建大小为max的临时数组
13 int[] temp = new int[max + 1];
14 //统计元素i出现的次数
15 for (int i = 0; i < n; i++) {
16 temp[arr[i]]++;
17 }
18 int k = 0;
19 //把临时数组统计好的数据汇总到原数组
20 for (int i = 0; i <= max; i++) {
21 for (int j = temp[i]; j > 0; j--) {
22 arr[k++] = i;
23 }
24 }
25 return arr;
26 }
27}
性质:1、时间复杂度:O(n+k) 2、空间复杂度:O(k) 3、稳定排序 4、非原地排序
注:K表示临时数组的大小,下同
优化一下
上面的代码中,我们是根据 max 的大小来创建对应大小的数组,假如原数组只有10个元素,并且最小值为 min = 10000,最大值为 max = 10005,那我们创建 10005 + 1 大小的数组不是很吃亏,最大值与最小值的差值为 5,所以我们创建大小为6的临时数组就可以了。
也就是说,我们创建的临时数组大小 (max - min + 1)就可以了,然后在把 min作为偏移量。优化之后的代码如下所示:
1public class Counting {
2 public static int[] sort(int[] arr) {
3 if(arr == null || arr.length < 2) return arr;
4
5 int n = arr.length;
6 int min = arr[0];
7 int max = arr[0];
8 // 寻找数组的最大值与最小值
9 for (int i = 1; i < n; i++) {
10 if(max < arr[i])
11 max = arr[i];
12 if(min > arr[i])
13 min = arr[i];
14 }
15 int d = max - min + 1;
16 //创建大小为max的临时数组
17 int[] temp = new int[d];
18 //统计元素i出现的次数
19 for (int i = 0; i < n; i++) {
20 temp[arr[i] - min]++;
21 }
22 int k = 0;
23 //把临时数组统计好的数据汇总到原数组
24 for (int i = 0; i < d; i++) {
25 for (int j = temp[i]; j > 0; j--) {
26 arr[k++] = i + min;
27 }
28 }
29 return arr;
30 }
31}
9、桶排序
桶排序就是把最大值和最小值之间的数进行瓜分,例如分成 10 个区间,10个区间对应10个桶,我们把各元素放到对应区间的桶中去,再对每个桶中的数进行排序,可以采用归并排序,也可以采用快速排序之类的。
之后每个桶里面的数据就是有序的了,我们在进行合并汇总。
为方便理解我还准备了图片:
如果还是不懂的话我还给你准备了优质的文章讲解:什么是桶排序?
代码如下:
1public class BucketSort {
2 public static int[] BucketSort(int[] arr) {
3 if(arr == null || arr.length < 2) return arr;
4
5 int n = arr.length;
6 int max = arr[0];
7 int min = arr[0];
8 // 寻找数组的最大值与最小值
9 for (int i = 1; i < n; i++) {
10 if(min > arr[i])
11 min = arr[i];
12 if(max < arr[i])
13 max = arr[i];
14 }
15 //和优化版本的计数排序一样,弄一个大小为 min 的偏移值
16 int d = max - min;
17 //创建 d / 5 + 1 个桶,第 i 桶存放 5*i ~ 5*i+5-1范围的数
18 int bucketNum = d / 5 + 1;
19 ArrayList<LinkedList<Integer>> bucketList = new ArrayList<>(bucketNum);
20 //初始化桶
21 for (int i = 0; i < bucketNum; i++) {
22 bucketList.add(new LinkedList<Integer>());
23 }
24 //遍历原数组,将每个元素放入桶中
25 for (int i = 0; i < n; i++) {
26 bucketList.get((arr[i]-min)/d).add(arr[i] - min);
27 }
28 //对桶内的元素进行排序,我这里采用系统自带的排序工具
29 for (int i = 0; i < bucketNum; i++) {
30 Collections.sort(bucketList.get(i));
31 }
32 //把每个桶排序好的数据进行合并汇总放回原数组
33 int k = 0;
34 for (int i = 0; i < bucketNum; i++) {
35 for (Integer t : bucketList.get(i)) {
36 arr[k++] = t + min;
37 }
38 }
39 return arr;
40 }
41}
性质:1、时间复杂度:O(n+k) 2、空间复杂度:O(n+k) 3、稳定排序 4、非原地排序
注:k 表示桶的个数,下同
10、基数排序
基数排序的排序思路是这样的:先以个位数的大小来对数据进行排序,接着以十位数的大小来多数进行排序,接着以百位数的大小……
排到最后,就是一组有序的元素了。不过,他在以某位数进行排序的时候,是用“桶”来排序的。
由于某位数(个位/十位….,不是一整个数)的大小范围为0-9,所以我们需要10个桶,然后把具有相同数值的数放进同一个桶里,之后再把桶里的数按照0号桶到9号桶的顺序取出来,这样一趟下来,按照某位数的排序就完成了
为方便理解我还准备了动图:

如果还是不懂的话我还给你准备了优质的文章讲解:为什么说O(n)复杂度的基数排序没有快速排序快?
代码如下:
1public class RadioSort {
2
3 public static int[] radioSort(int[] arr) {
4 if(arr == null || arr.length < 2) return arr;
5
6 int n = arr.length;
7 int max = arr[0];
8 // 找出最大值
9 for (int i = 1; i < n; i++) {
10 if(max < arr[i]) max = arr[i];
11 }
12 // 计算最大值是几位数
13 int num = 1;
14 while (max / 10 > 0) {
15 num++;
16 max = max / 10;
17 }
18 // 创建10个桶
19 ArrayList<LinkedList<Integer>> bucketList = new ArrayList<>(10);
20 //初始化桶
21 for (int i = 0; i < 10; i++) {
22 bucketList.add(new LinkedList<Integer>());
23 }
24 // 进行每一趟的排序,从个位数开始排
25 for (int i = 1; i <= num; i++) {
26 for (int j = 0; j < n; j++) {
27 // 获取每个数最后第 i 位是数组
28 int radio = (arr[j] / (int)Math.pow(10,i-1)) % 10;
29 //放进对应的桶里
30 bucketList.get(radio).add(arr[j]);
31 }
32 //合并放回原数组
33 int k = 0;
34 for (int j = 0; j < 10; j++) {
35 for (Integer t : bucketList.get(j)) {
36 arr[k++] = t;
37 }
38 //取出来合并了之后把桶清光数据
39 bucketList.get(j).clear();
40 }
41 }
42 return arr;
43 }
44}
性质:1、时间复杂度:O(kn) 2、空间复杂度:O(n+k) 3、稳定排序 4、非原地排序
总结
用一张图汇总了10大排序算法的性质
如果你是复习/学习十大排序算法,一定要自己不看示例代码手动实现一遍,一定要自己不看示例代码手动实现一遍,一定要自己不看示例代码手动实现一遍。
转载自十大算法

java 实现十大经典算法
1. 二分查找算法(非递归)
/**
* @desc 二分查询(非递归方式)
* 案例:
* {1,3,8,10,11,67,100},编程实现二分查找,要求使用非递归方式完成。
* @Author xw
* @Date 2019/9/27
*/
public class BinarySearchNonRecursive {
public static void main(String[] args) {
int[] arr = {1, 3, 8, 10, 11, 67, 100};
int index = binarySearch(arr, 1);
if (index != -1) {
System.out.println("找到了,下标为:" + index);
} else {
System.out.println("没有找到--");
}
}
private static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] > target) {
right = mid - 1; // 向左找
} else {
left = mid + 1; // 向右找
}
}
return -1;
}
}2. 分治算法
/**
* @desc 分治算法案例:汉诺塔
* (1)基本概念
* 分治算法是一种很重要的算法,字面上的解释是“分而治之”,就是把一个复杂的问题
* 分解成两个或更多的相同或相似的子问题...直到最后子问题可以简单的直接求解,原
* 问题的解即子问题的解的合并,这个技巧就是很多高效算法的基础,如排序算法(快速排序,归并排序),傅里叶变换(快速傅里叶变换)...
* (2)基本步骤
* 1)分解:将原问题分解为若干个规模较小的问题,相互独立,与原问题形式相同的子问题
* 2)解决:若子问题规模较小则直接解决,否则递归地解各个子问题
* 3)合并:将各个子问题的解合并为原问题的解
* (3)分治算法设计模式
* if |P|<=n0
* then return (ADHOC(P))
* // 将P分解为较小的问题P1,P2...PK
* for i <- 1 to k
* do yi <- Divide-and-Conquer(Pi) 递归解决Pi
* T <- MERGE(y1,y2...yk) 合并子问题
* return (T)
* <p>
* |P|:表示问题P的规模
* n0:表示阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。
* ADHOC(P):是该分治法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过n0时直接用算法ADHOC(P)求解
* 算法MERGE(y1,y2...yk):是该分治算法中的合并子算法,用于将P的子问题P1,P2...PK的相应的解y1,y2,..yk合并为P的解。
* <p>
* 经典案例:汉诺塔
* 思路分析:
* (1)如果有一个盘,A->C
* n0=2
* if (n<=n0) {
* // 直接解出来
* }
* // 将P分解为较小的问题P1,P2...PK
* while(n>n0) {
* 分(n);
* n--;
* }
* // T <- MERGE(y1,y2...yk) 合并子问题
* @Author xw
* @Date 2019/9/27
*/
public class HanoiTower {
public static void main(String[] args) {
hanoiTower(3, ''A'', ''B'', ''C'');
}
private static void hanoiTower(int num, char a, char b, char c) {
if (num == 1) { // 只有一个盘,直接解出
System.out.println("第1个盘从" + a + "->" + c);
} else {
// 如果n>=2的情况
// 1.先把最上面的所有盘A->B,移动过程会使用C
hanoiTower(num - 1, a, c, b);
// 2.把最下边的盘A->C
System.out.println("第" + num + "个盘从" + a + "->" + c);
// 3.把B塔所有盘从B->C,移动过程使用到A
hanoiTower(num - 1, b, a, c);
}
}
}
3. 动态规划算法


/**
* @desc 动态规划算法案例:背包问题
* 思路分析:
* (1)假设:
* 用w[i],v[i]来确定是否需要将该物品放入背包中;
* 即对于给定的n个物品,设v[i],w[i]分别为第i个物品的价值和重量,C为背包的容量。
* 再令v[i][j] 表示在前i个物品中能够装入容量j的背包的最大价值。则我们有下面的结果:
* (2)结论:
* 1)当v[i][0]=v[0][j]=0; // 表示填入表 第一行和第一列是0
* 2)当w[i]>j时;v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于当前背包的容量时,就直接使用上一个单元格的装入策略
* 3)当j>=w[i]时;v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
* // 当准入的新增的商品的容量小于等于当前背包的容量,装入方式:
* v[i-1][j]:就是上一个单元格的装入的最大值
* v[i]:表示当前商品的价值
* v[i-1][j-w[i]]:装入i-1商品,到剩余空间j-w[i]的最大值
* 当j>=w[i]时:v[i][j] = max{v[i-1][j], v[i-1][j-w[i]]}
* <p>
* 案例:
* 物品 重量 价格
* 吉他(G) 1 1500
* 音响(S) 4 3000
* 电脑(L) 3 2000
* @Author xw
* @Date 2019/9/27
*/
public class KnapsackProblem {
public static void main(String[] args) {
int[] w = {1, 4, 3}; // 物品重量
int[] val = {1500, 3000, 2000}; // 物品价值
int m = 4; // 背包的容量
int n = val.length; // 物品个数
// 创建二维数据
int[][] v = new int[n + 1][m + 1];
// 1)当v[i][0]=v[0][j]=0; // 表示填入表 第一行和第一列是0
for (int i = 0; i < v.length; i++) {
v[0][i] = 0; // 第一列为0
}
for (int i = 0; i < v.length; i++) {
v[i][0] = 0; // 第一行为0
}
int[][] path = new int[n + 1][m + 1];
for (int i = 1; i < v.length; i++) {
for (int j = 1; j < v[0].length; j++) { // 不处理第1列
// 当w[i]>j时;v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于当前背包的容量时,就直接使用上一个单元格的装入策略
if (w[i - 1] > j) {
v[i][j] = v[i - 1][j];
} else {
// 当j>=w[i]时;v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
// v[i-1][j]:就是上一个单元格的装入的最大值
// v[i]:表示当前商品的价值
// v[i-1][j-w[i]]:装入i-1商品,到剩余空间j-w[i]的最大值
// 当准入的新增的商品的容量小于等于当前背包的容量,装入方式:
if (v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) { // w[i]->w[i-1]替换?
v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
// 把当前的情况记录到path
path[i][j] = 1;
} else {
v[i][j] = v[i - 1][j];
}
}
}
}
// 输出一把
for (int i = 0; i < v.length; i++) {
for (int j = 0; j < v[i].length; j++) {
System.out.print(v[i][j] + "\t");
}
System.out.println();
}
System.out.println("========================");
/*for (int i = 0; i < path.length; i++) {
for (int j = 0; j < path[i].length; j++) {
if (path[i][j] == 1) {
System.out.println(String.format("第%d个商品放入背包", i));
}
}
}*/
// 其实我们只需要最后的放入
int i = path.length - 1;
int j = path[0].length - 1;
while (i > 0 && j > 0) {
if (path[i][j] == 1) {
System.out.println(String.format("第%d个商品放入到背包", i));
j -= w[i - 1];
}
i--;
}
}
}
4.KMP 算法


/**
* @desc KMP算法
* 基本介绍:
* (1)暴力匹配算法
* 1)如果当前字符匹配成功(即str1[i]=str2[i]),则i++,j++,继续匹配下一个字符
* 2)如果失败,令i=i-(j-1),j=0,相当于每次匹配失败时,i回溯,j被转为0
* 3)用暴力方法解决的话就会有大量的回溯,每次只移动一位,若是不匹配,移动到下一位接着判断,浪费大量时间。(不可行)
* 4)暴力匹配实现
* (2)KMP算法介绍
* 1)KMP是一个解决模式串在文本串是否出现过,如果出现过,最早出现的位置就经典算法。
* 2)Knuth-Morris-Pratt字符串查找法,简称KMP。
* 3)KMP算法就是利用之前判断过信息,通过一个next数组,保存模式串中前后最长公共序列的长度,每次回溯时,通过next数组找到,
* 前面匹配的位置,省去了大量的计算时间
* 4)参考资料:https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html
* @Author xw
* @Date 2019/9/27
*/
public class KMPAlgorithm {
public static void main(String[] args) {
// 暴力匹配
String str1 = "ABCDE";
String str2 = "CD";
int index = violenceMatch(str1, str2);
if (index != -1) {
System.out.println("找到了,位置:" + index);
} else {
System.out.println("没有找到!");
}
// KMP算法介绍
// 字符串模板匹配值
str1 = "BBC ABCDAD ABCDABCDABDE";
str2 = "ABCDABD";
/*int[] next = kmpNext("ABCDABD");
System.out.println("next=" + Arrays.toString(next));*/
index = kmpMatch(str1, str2, kmpNext(str2));
if (index != -1) {
System.out.println("找到了,位置:" + index);
} else {
System.out.println("没有找到!");
}
}
}
5. 贪心算法


/**
* @desc 贪心算法
* 思路分析
* (1)使用穷举法,列出每个可能广播台集合,这被称为幂集。
* (2)假设有n个广播台,则广播台的组合共有2^n-1个,假设每秒可以计算10个子集
* 广播台数量 子集总数 需要的时间
* 5 32 3.2秒
* 10 1024 102.4秒
* ...
*
* 案例:集合覆盖问题
* 假设存在下面需要付费的广播台,以及广播信号可以覆盖的地区,如何选择
* 最少的广播台,让所有的地区都可以接收信息
* 广播台 覆盖地区
* K1 "北京","上海","天津"
* K2 "广州","北京","深圳"
* K3 "成都","上海","杭州"
* K4 "上海","天津"
* K5 "杭州","大连"
* @Author xw
* @Date 2019/9/27
*/
public class GreedyAlgorithm {
public static void main(String[] args) {
Map<String, Set<String>> broadcasts = new HashMap<>(); // 广播电台
broadcasts.put("K1", Arrays.stream(new String[]{"北京", "上海", "天津"}).collect(Collectors.toSet()));
broadcasts.put("K2", Arrays.stream(new String[]{"广州", "北京", "深圳"}).collect(Collectors.toSet()));
broadcasts.put("K3", Arrays.stream(new String[]{"成都", "上海", "杭州"}).collect(Collectors.toSet()));
broadcasts.put("K4", Arrays.stream(new String[]{"上海", "天津"}).collect(Collectors.toSet()));
broadcasts.put("K5", Arrays.stream(new String[]{"杭州", "大连"}).collect(Collectors.toSet()));
// [上海, 天津, 北京, 广州, 深圳, 成都, 杭州, 大连]
List<String> allAreas = broadcasts.values().stream().flatMap(Collection::stream).distinct().collect(Collectors.toList()); // 表示所有需要覆盖的地区
System.out.println("allAreas=" + allAreas);
List<String> selects = new ArrayList<>(); // 选择的地区集合
// 定义一个临时的集合,在遍历过程中,存放遍历过程中的电台覆盖的地区和当前还没有覆盖的地区的交集
Set<String> tempSet = new HashSet<>();
String maxKey; // 最大的电台,保存在一次遍历过程中,能够覆盖最大未覆盖的地区对应的电台key
while (allAreas.size() != 0) {
maxKey = null; // 置空
// 遍历broadcasts,取出对应key
for (String key : broadcasts.keySet()) {
tempSet.clear(); // 清空
Set<String> areas = broadcasts.get(key);
tempSet.addAll(areas);
tempSet.retainAll(allAreas); // tempSet = tempSet与allAreas的交集
if (tempSet.size() > 0 && (maxKey == null
|| tempSet.size() > broadcasts.get(maxKey).size())) {
maxKey = key;
}
}
if (maxKey != null) {
selects.add(maxKey);
// 将maxKey指向的广播电台覆盖地区,从allAreas去掉
System.out.println("maxKey=" + maxKey);
allAreas.removeAll(broadcasts.get(maxKey));
}
}
System.out.println("得到的选择结果是:" + selects);
}
}
6. 普利姆算法


/**
* @desc 普利姆算法
* 应用案例:修路问题
* <p>
* 思路分析
* 1.从<A>顶点开始处理=><A,G> 2
* A,C[7] A-G[2] A-B[5] =>
* 2.<A,G>开始,将A和G顶点和他们相邻的还没有访问的顶面进行处理=> <A,G,B>
* A-C[7] A-B[5] G-B[3] G-F[6]
* 3.<A,G,B>开始,将A,G,B顶点和他们相邻的还没有访问的顶面进行处理=> <A,G,B>
* A-C[7] G-E[4] G-F[6] B-D[9]
* ...
* 4.{A,G,B,E,F,D} -> C // 第6次大循环,对应边<A,C>权值:7 => <A,G,B,E,F,D,C>
* @Author xw
* @Date 2019/10/4
*/
public class PrimAlgorithm {
public static void main(String[] args) {
char[] data = {''A'',''B'',''C'',''D'',''E'',''F'',''G''};
int verxs = data.length;
// 邻接矩阵
int[][] weight = new int[][] {
{10000,5,7,10000,10000,10000,2},
{5,10000,10000,9,10000,10000,3},
{7,10000,10000,10000,8,10000,10000},
{10000,9,10000,10000,10000,4,10000},
{10000,10000,8,10000,10000,5,4},
{10000,10000,10000,4,5,10000,6},
{2,3,10000,10000,4,6,10000}
};
// 创建MGraph对象
MGraph graph = new MGraph(verxs);
// 创建最小树
MinTree minTree = new MinTree();
minTree.createGraph(graph, verxs, data, weight);
// 输出
minTree.showGraph(graph);
// 测试普利姆算法
minTree.prim(graph, 0);
}
}
7. 克鲁斯卡尔算法


/**
* @desc 克鲁斯卡尔算法
* 案例:公交车问题
* 1. 某城市新增7个站点,A,B,C,D,E,F,G,现在需要修路7个站点连通
* 2. 各个站点距离用连线表示,比如A-B距离12公里
* 3. 问:如何修路保证各个站点都能连通,并且总的修建公路总里程最短
* @Author xw
* @Date 2019/10/8
*/
public class KruskalCase {
private static final int INF = Integer.MAX_VALUE;
private char[] vertexs;
private int[][] matrix;
private int edgeNums; // 边的数量
public KruskalCase(char[] vertexs,int[][] matrix ) {
this.vertexs = vertexs;
this.matrix = matrix;
// 统计边
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) { // 每次少一条边,所以是i+1
if (this.matrix[i][j] != INF) {
edgeNums++;
}
}
}
}
public static void main(String[] args) {
char[] vertexs = {''A'', ''B'', ''C'', ''D'', ''E'', ''F'', ''G''};
int[][] matrix = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/{ 0, 12, INF, INF, INF, 16, 14 },
/*B*/{ 12, 0, 10, INF, INF, 7, INF},
/*C*/{ INF, 10, 0, 3, 5, 6, INF },
/*D*/{ INF, INF, 3, 0, 4, INF, INF },
/*E*/{ INF, INF, 5, 4, 0, 2, 8 },
/*F*/{ 16, 7, 6, INF, 2, 0, 9 },
/*G*/{ 14, INF, INF, INF, 8, 9, 0 }
};
// 创建KruskalCase对象实例
KruskalCase kruskalCase = new KruskalCase(vertexs, matrix);
//
kruskalCase.print();
kruskalCase.kruskal();
}
}
8. 迪杰斯特拉算法


/**
* @desc 迪杰斯特拉算法
* 案例:最短路径问题
* 1. 战争时期,胜利乡有7个村庄(A,B,C,D,E,F,G),现在有6个邮差,从G点出发,需要分别把邮件分别送到A,B,C,D,E,F 六个村庄
* 2. 各个村庄的距离用边线表示(权),比如A-B距离5公里
* 3. 问:如何计算最短距离
*
* @Author xw
* @Date 2019/10/8
*/
public class DijkstraAlgorithm {
public static void main(String[] args) {
char[] vertex = {''A'', ''B'', ''C'', ''D'', ''E'', ''F'', ''G''};
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;
matrix[0] = new int[]{N,5,7,N,N,N,2};
matrix[1] = new int[]{5,N,N,9,N,N,3};
matrix[2] = new int[]{7,N,N,N,8,N,N};
matrix[3] = new int[]{N,9,N,N,N,4,N};
matrix[4] = new int[]{N,N,8,N,N,5,4};
matrix[5] = new int[]{N,N,N,4,5,N,6};
matrix[6] = new int[]{2,3,N,N,4,6,N};
// 创建Graph对象
Graph graph = new Graph(vertex, matrix);
graph.showGraph();
// 测试迪杰斯特拉算法
graph.dsj(6); // G
graph.showDijkstra();
}
}
9. 弗洛伊德算法


/**
* @desc 弗洛伊德算法
* @Author xw
* @Date 2019/10/8
*/
public class FloydAlgorithm {
public static void main(String[] args) {
char[] vertex = {''A'', ''B'', ''C'', ''D'', ''E'', ''F'', ''G''};
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;
matrix[0] = new int[]{0, 5, 7, N, N, N, 2};
matrix[1] = new int[]{5, 0, N, 9, N, N, 3};
matrix[2] = new int[]{7, N, 0, N, 8, N, N};
matrix[3] = new int[]{N, 9, N, 0, N, 4, N};
matrix[4] = new int[]{N, N, 8, N, 0, 5, 4};
matrix[5] = new int[]{N, N, N, 4, 5, 0, 6};
matrix[6] = new int[]{2, 3, N, N, 4, 6, 0};
FloydGraph graph = new FloydGraph(vertex.length, matrix, vertex);
graph.floyd();
graph.show();
}
}
10. 马踏棋盘算法


/**
* @desc 马踏棋盘算法
* @Author xw
* @Date 2019/10/8
*/
public class HorseChessboard {
private static int X; // 棋盘的列数
private static int Y; // 棋盘的行数
//创建一个数组,标记棋盘的各个位置是否被访问过
private static boolean visited[];
//使用一个属性,标记是否棋盘的所有位置都被访问
private static boolean finished; // 如果为true,表示成功
public static void main(String[] args) {
System.out.println("骑士周游算法,开始运行~~");
//测试骑士周游算法是否正确
X = 8;
Y = 8;
int row = 1; //马儿初始位置的行,从1开始编号
int column = 1; //马儿初始位置的列,从1开始编号
//创建棋盘
int[][] chessboard = new int[X][Y];
visited = new boolean[X * Y];//初始值都是false
//测试一下耗时
long start = System.currentTimeMillis();
traversalChessboard(chessboard, row - 1, column - 1, 1);
long end = System.currentTimeMillis();
System.out.println("共耗时: " + (end - start) + " 毫秒");
//输出棋盘的最后情况
for(int[] rows : chessboard) {
for(int step: rows) {
System.out.print(step + "\t");
}
System.out.println();
}
}
}gitee 地址:https://gitee.com/linestyle007/jucdemo2
博客地址:https://linestyle007.gitee.io/
github 地址:https://github.com/line007/jucdemo2

JAVA十大经典算法总结
0、排序算法说明
·0.1 排序的定义
对一序列对象根据某个关键字进行排序。
·0.2 术语说明
·稳定 :如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
·不稳定 :如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
·内排序 :所有排序操作都在内存中完成;
·外排序 :由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
·时间复杂度 : 一个算法执行所耗费的时间。
·空间复杂度 :运行完一个程序所需内存的大小。
·0.3 算法总结
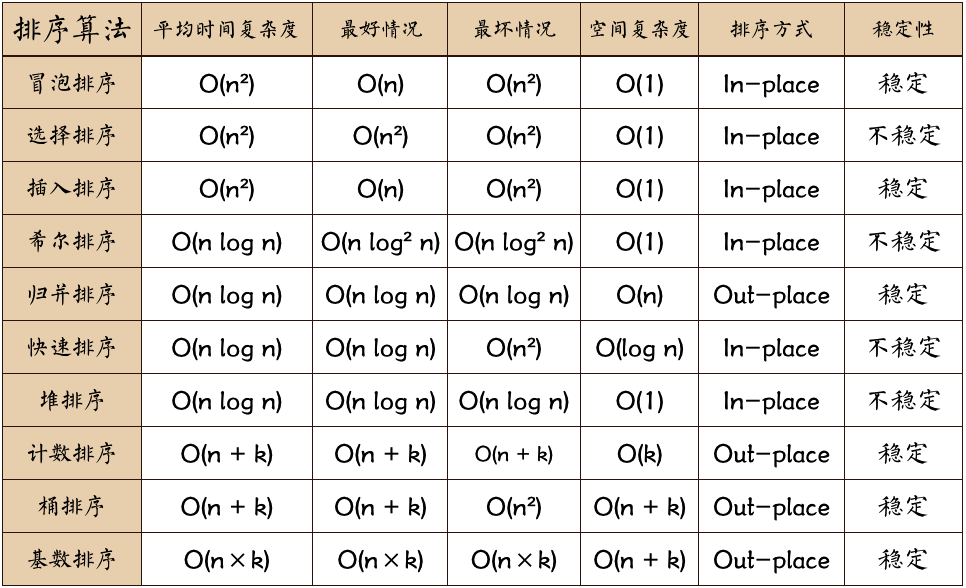
·图片名词解释:
·n: 数据规模
·k: “桶”的个数
·In-place: 占用常数内存,不占用额外内存
·Out-place: 占用额外内存
·0.5 算法分类
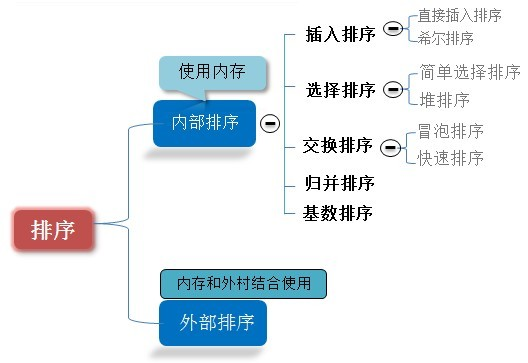
·0.6 比较和非比较的区别
常见的快速排序、归并排序、堆排序、冒泡排序 等属于比较排序 。在排序的最终结果里,元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较,才能确定自己的位置 。
在冒泡排序之类的排序中,问题规模为n,又因为需要比较n次,所以平均时间复杂度为O(n²)。在归并排序、快速排序之类的排序中,问题规模通过分治法消减为logN次,所以时间复杂度平均O(nlogn)。
比较排序的优势是,适用于各种规模的数据,也不在乎数据的分布,都能进行排序。可以说,比较排序适用于一切需要排序的情况。
计数排序、基数排序、桶排序则属于非比较排序 。非比较排序是通过确定每个元素之前,应该有多少个元素来排序。针对数组arr,计算arr[i]之前有多少个元素,则唯一确定了arr[i]在排序后数组中的位置 。
非比较排序只要确定每个元素之前的已有的元素个数即可,所有一次遍历即可解决。算法时间复杂度O(n)。
非比较排序时间复杂度底,但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。
1、冒泡排序(Bubble Sort)
冒泡排序 是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1.3 代码实现
1.1 算法描述
步骤1: 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
步骤2: 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
步骤3: 针对所有的元素重复以上的步骤,除了最后一个;
步骤4: 重复步骤1~3,直到排序完成。
1.2 动图演示
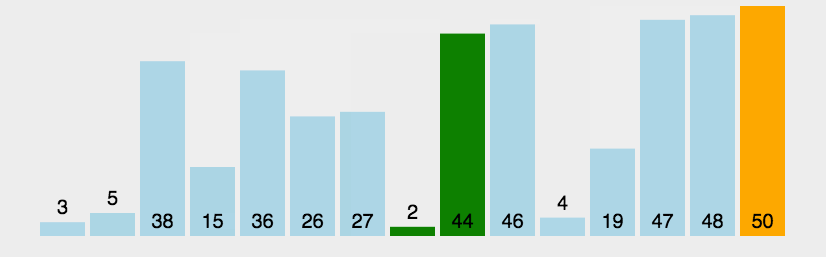
1.3 代码实现
/**
* 冒泡排序
*
* @param array
* @return
*/
public static int[] bubbleSort(int[] array) {
if (array.length == 0)
return array;
for (int i = 0; i < array.length; i++)
for (int j = 0; j < array.length - 1 - i; j++)
if (array[j + 1] < array[j]) {
int temp = array[j + 1];
array[j + 1] = array[j];
array[j] = temp;
}
return array;
}
1.4 算法分析
最佳情况:T(n) = O(n)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(n2)
2、选择排序(Selection Sort)
选择排序 是表现最稳定的排序算法之一 ,因为无论什么数据进去都是O(n2)的时间复杂度 ,所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧。
选择排序(Selection-sort) 是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
2.1 算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
步骤1:初始状态:无序区为R[1…n],有序区为空;
步骤2:第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1…i-1]和R(i…n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
步骤3:n-1趟结束,数组有序化了。
2.2 动图演示
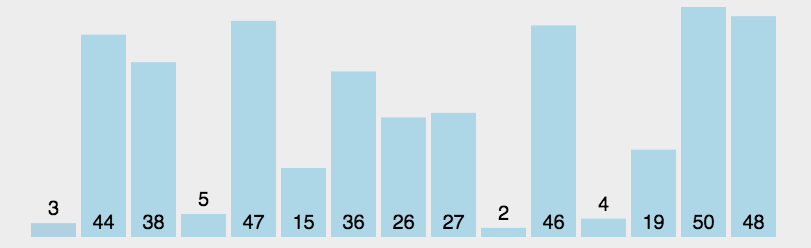
2.3 代码实现
/**
* 选择排序
* @param array
* @return
*/
public static int[] selectionSort(int[] array) {
if (array.length == 0)
return array;
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i; j < array.length; j++) {
if (array[j] < array[minIndex]) //找到最小的数
minIndex = j; //将最小数的索引保存
}
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
return array;
}
2.4 算法分析
最佳情况:T(n) = O(n2)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(n2)
3、插入排序(Insertion Sort)
插入排序(Insertion-Sort) 的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
3.1 算法描述
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
步骤1: 从第一个元素开始,该元素可以认为已经被排序;
步骤2: 取出下一个元素,在已经排序的元素序列中从后向前扫描;
步骤3: 如果该元素(已排序)大于新元素,将该元素移到下一位置;
步骤4: 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
步骤5: 将新元素插入到该位置后;
步骤6: 重复步骤2~5。
3.2 动图演示
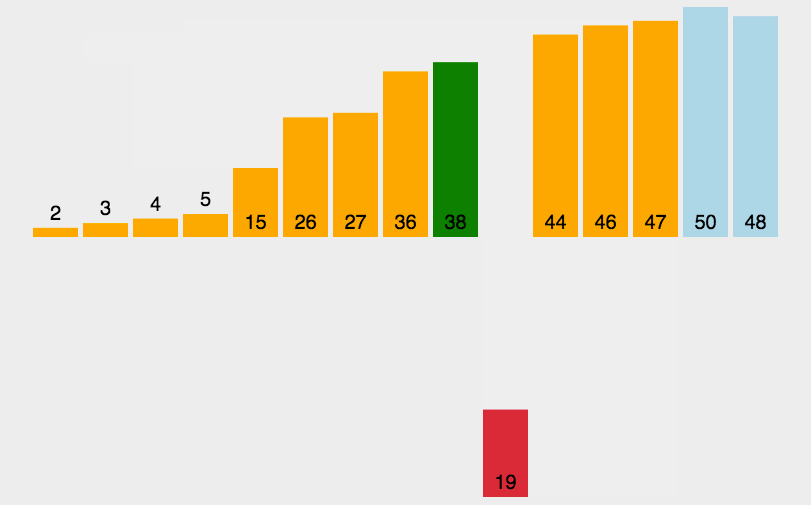
3.3 代码实现
/**
* 插入排序
* @param array
* @return
*/
public static int[] insertionSort(int[] array) {
if (array.length == 0)
return array;
int current;
for (int i = 0; i < array.length - 1; i++) {
current = array[i + 1];
int preIndex = i;
while (preIndex >= 0 && current < array[preIndex]) {
array[preIndex + 1] = array[preIndex];
preIndex--;
}
array[preIndex + 1] = current;
}
return array;
}3.4 算法分析
最佳情况:T(n) = O(n)
最坏情况:T(n) = O(n2)
平均情况:T(n) = O(n2)
4、希尔排序(Shell Sort)
希尔排序是希尔(Donald Shell) 于1959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破O(n2)的第一批算法之一。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
希尔排序是把记录按下表的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
4.1 算法描述
我们来看下希尔排序的基本步骤,在此我们选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2,(n/2)/2…1},称为增量序列。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
步骤1:选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
步骤2:按增量序列个数k,对序列进行k 趟排序;
步骤3:每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
4.2 过程演示
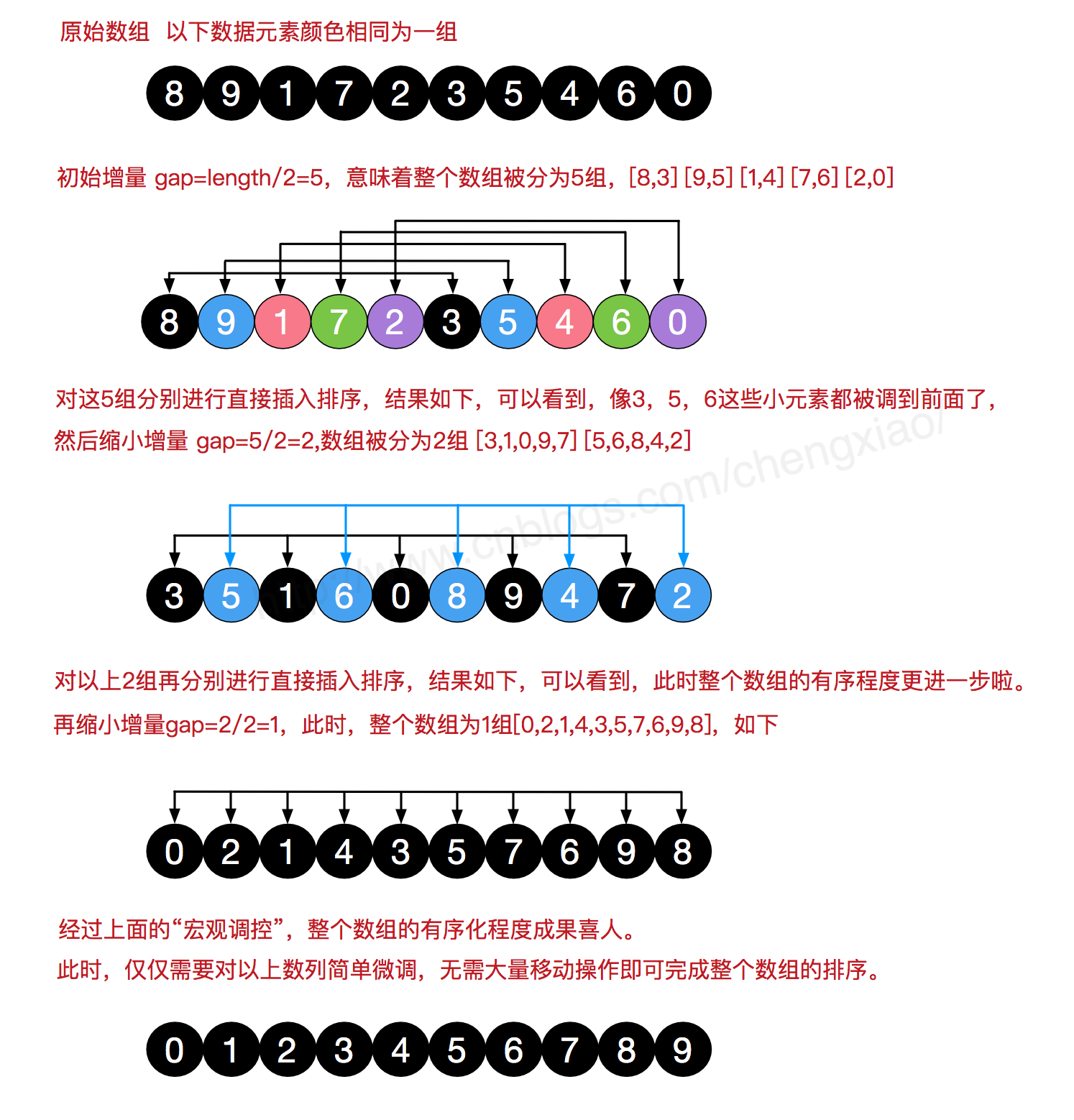
4.3 代码实现
/**
* 希尔排序
*
* @param array
* @return
*/
public static int[] ShellSort(int[] array) {
int len = array.length;
int temp, gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
temp = array[i];
int preIndex = i - gap;
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
array[preIndex + gap] = temp;
}
gap /= 2;
}
return array;
}4.4 算法分析
最佳情况:T(n) = O(nlog2 n)
最坏情况:T(n) = O(nlog2 n)
平均情况:T(n) =O(nlog2n)
5、归并排序(Merge Sort)
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。
归并排序 是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
5.1 算法描述
步骤1:把长度为n的输入序列分成两个长度为n/2的子序列;
步骤2:对这两个子序列分别采用归并排序;
步骤3:将两个排序好的子序列合并成一个最终的排序序列。
5.2 动图演示
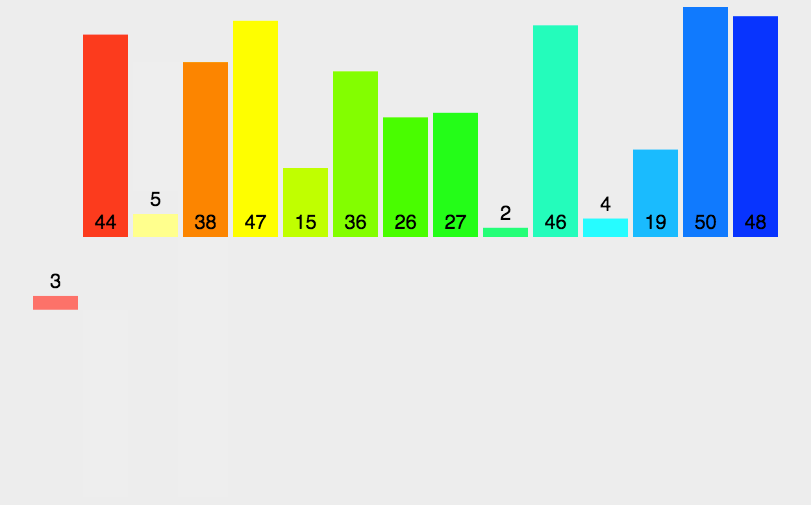
5.3 代码实现
/**
* 归并排序
*
* @param array
* @return
*/
public static int[] MergeSort(int[] array) {
if (array.length < 2) return array;
int mid = array.length / 2;
int[] left = Arrays.copyOfRange(array, 0, mid);
int[] right = Arrays.copyOfRange(array, mid, array.length);
return merge(MergeSort(left), MergeSort(right));
}
/**
* 归并排序——将两段排序好的数组结合成一个排序数组
*
* @param left
* @param right
* @return
*/
public static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
for (int index = 0, i = 0, j = 0; index < result.length; index++) {
if (i >= left.length)
result[index] = right[j++];
else if (j >= right.length)
result[index] = left[i++];
else if (left[i] > right[j])
result[index] = right[j++];
else
result[index] = left[i++];
}
return result;
}5.4 算法分析
最佳情况:T(n) = O(n)
最差情况:T(n) = O(nlogn)
平均情况:T(n) = O(nlogn)
6、快速排序(Quick Sort)
快速排序 的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
6.1 算法描述
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
步骤1:从数列中挑出一个元素,称为 “基准”(pivot );
步骤2:重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
步骤3:递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
6.2 动图演示
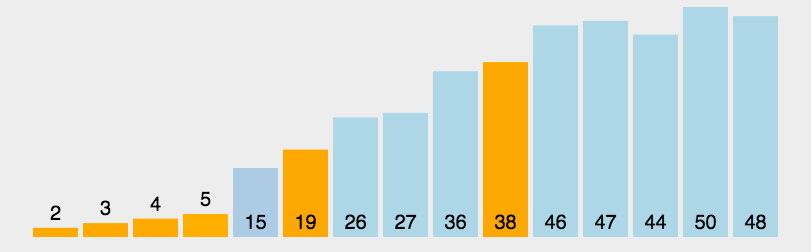
6.3 代码实现
/**
* 快速排序方法
* @param array
* @param start
* @param end
* @return
*/
public static int[] QuickSort(int[] array, int start, int end) {
if (array.length < 1 || start < 0 || end >= array.length || start > end) return null;
int smallIndex = partition(array, start, end);
if (smallIndex > start)
QuickSort(array, start, smallIndex - 1);
if (smallIndex < end)
QuickSort(array, smallIndex + 1, end);
return array;
}
/**
* 快速排序算法——partition
* @param array
* @param start
* @param end
* @return
*/
public static int partition(int[] array, int start, int end) {
int pivot = (int) (start + Math.random() * (end - start + 1));
int smallIndex = start - 1;
swap(array, pivot, end);
for (int i = start; i <= end; i++)
if (array[i] <= array[end]) {
smallIndex++;
if (i > smallIndex)
swap(array, i, smallIndex);
}
return smallIndex;
}
/**
* 交换数组内两个元素
* @param array
* @param i
* @param j
*/
public static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}6.4 算法分析
最佳情况:T(n) = O(nlogn)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(nlogn)
7、堆排序(Heap Sort)
堆排序(Heapsort) 是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
7.1 算法描述
步骤1:将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
步骤2:将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
步骤3:由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
7.2 动图演示

7.3 代码实现
注意:这里用到了完全二叉树的部分性质:详情见数据结构二叉树知识点
//声明全局变量,用于记录数组array的长度;
static int len;
/**
* 堆排序算法
*
* @param array
* @return
*/
public static int[] HeapSort(int[] array) {
len = array.length;
if (len < 1) return array;
//1.构建一个最大堆
buildMaxHeap(array);
//2.循环将堆首位(最大值)与末位交换,然后在重新调整最大堆
while (len > 0) {
swap(array, 0, len - 1);
len--;
adjustHeap(array, 0);
}
return array;
}
/**
* 建立最大堆
*
* @param array
*/
public static void buildMaxHeap(int[] array) {
//从最后一个非叶子节点开始向上构造最大堆
//for循环这样写会更好一点:i的左子树和右子树分别2i+1和2(i+1)
for (int i = (len/2- 1); i >= 0; i--) {
adjustHeap(array, i);
}
}
/**
* 调整使之成为最大堆
*
* @param array
* @param i
*/
public static void adjustHeap(int[] array, int i) {
int maxIndex = i;
//如果有左子树,且左子树大于父节点,则将最大指针指向左子树
if (i * 2 < len && array[i * 2] > array[maxIndex])
maxIndex = i * 2+1; //感谢网友矫正,之前是i*2
//如果有右子树,且右子树大于父节点,则将最大指针指向右子树
if (i * 2 + 1 < len && array[i * 2 + 1] > array[maxIndex])
maxIndex = i * 2 + 2; //感谢网友矫正,之前是i*2+1
//如果父节点不是最大值,则将父节点与最大值交换,并且递归调整与父节点交换的位置。
if (maxIndex != i) {
swap(array, maxIndex, i);
adjustHeap(array, maxIndex);
}
}7.4 算法分析
最佳情况:T(n) = O(nlogn)
最差情况:T(n) = O(nlogn)
平均情况:T(n) = O(nlogn)
8、计数排序(Counting Sort)
计数排序 的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
计数排序(Counting sort) 是一种稳定的排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。
8.1 算法描述
步骤1:找出待排序的数组中最大和最小的元素;
步骤2:统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
步骤3:对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
步骤4:反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
8.2 动图演示
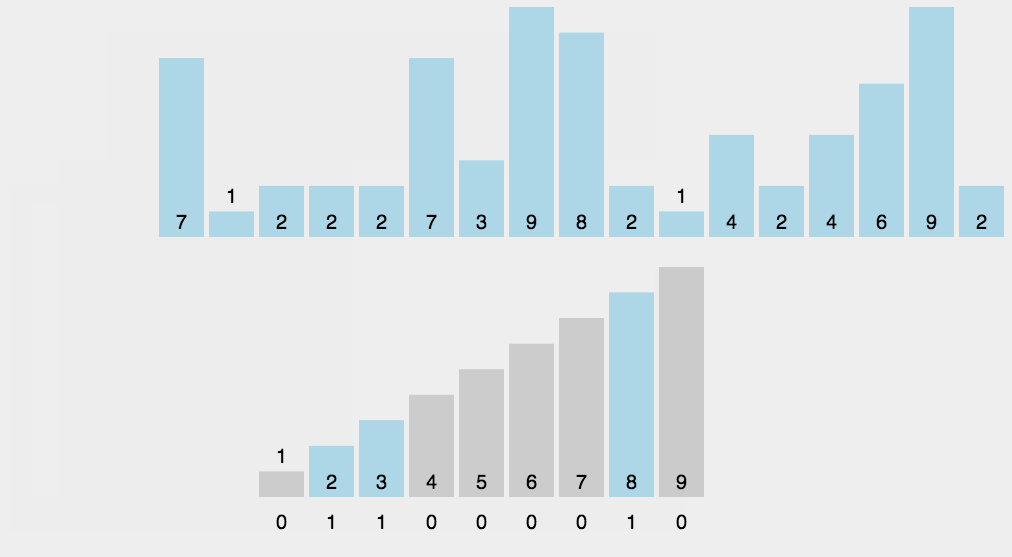
8.3 代码实现
/**
* 计数排序
*
* @param array
* @return
*/
public static int[] CountingSort(int[] array) {
if (array.length == 0) return array;
int bias, min = array[0], max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max)
max = array[i];
if (array[i] < min)
min = array[i];
}
bias = 0 - min;
int[] bucket = new int[max - min + 1];
Arrays.fill(bucket, 0);
for (int i = 0; i < array.length; i++) {
bucket[array[i] + bias]++;
}
int index = 0, i = 0;
while (index < array.length) {
if (bucket[i] != 0) {
array[index] = i - bias;
bucket[i]--;
index++;
} else
i++;
}
return array;
}8.4 算法分析
当输入的元素是n 个0到k之间的整数时,它的运行时间是 O(n + k)。计数排序不是比较排序,排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围(等于待排序数组的最大值与最小值的差加上1),这使得计数排序对于数据范围很大的数组,需要大量时间和内存。
最佳情况:T(n) = O(n+k)
最差情况:T(n) = O(n+k)
平均情况:T(n) = O(n+k)
9、桶排序(Bucket Sort)
桶排序 是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
桶排序 (Bucket sort)的工作的原理:
假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排
9.1 算法描述
步骤1:人为设置一个BucketSize,作为每个桶所能放置多少个不同数值(例如当BucketSize==5时,该桶可以存放{1,2,3,4,5}这几种数字,但是容量不限,即可以存放100个3);
步骤2:遍历输入数据,并且把数据一个一个放到对应的桶里去;
步骤3:对每个不是空的桶进行排序,可以使用其它排序方法,也可以递归使用桶排序;
步骤4:从不是空的桶里把排好序的数据拼接起来。
注意,如果递归使用桶排序为各个桶排序,则当桶数量为1时要手动减小BucketSize增加下一循环桶的数量,否则会陷入死循环,导致内存溢出。
9.2 图片演示
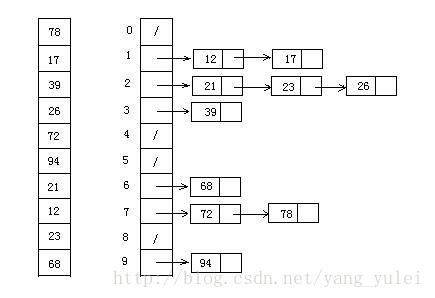
9.3 代码实现
/**
* 桶排序
*
* @param array
* @param bucketSize
* @return
*/
public static ArrayList<Integer> BucketSort(ArrayList<Integer> array, int bucketSize) {
if (array == null || array.size() < 2)
return array;
int max = array.get(0), min = array.get(0);
// 找到最大值最小值
for (int i = 0; i < array.size(); i++) {
if (array.get(i) > max)
max = array.get(i);
if (array.get(i) < min)
min = array.get(i);
}
int bucketCount = (max - min) / bucketSize + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketCount);
ArrayList<Integer> resultArr = new ArrayList<>();
for (int i = 0; i < bucketCount; i++) {
bucketArr.add(new ArrayList<Integer>());
}
for (int i = 0; i < array.size(); i++) {
bucketArr.get((array.get(i) - min) / bucketSize).add(array.get(i));
}
for (int i = 0; i < bucketCount; i++) {
if (bucketSize == 1) { // 如果带排序数组中有重复数字时
for (int j = 0; j < bucketArr.get(i).size(); j++)
resultArr.add(bucketArr.get(i).get(j));
} else {
if (bucketCount == 1)
bucketSize--;
ArrayList<Integer> temp = BucketSort(bucketArr.get(i), bucketSize);
for (int j = 0; j < temp.size(); j++)
resultArr.add(temp.get(j));
}
}
return resultArr;
}9.4 算法分析
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
最佳情况:T(n) = O(n+k)
最差情况:T(n) = O(n+k)
平均情况:T(n) = O(n2)
10、基数排序(Radix Sort)
基数排序也是非比较的排序算法,对每一位进行排序,从最低位开始排序,复杂度为O(kn),为数组长度,k为数组中的数的最大的位数;
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
10.1 算法描述
步骤1:取得数组中的最大数,并取得位数;
步骤2:arr为原始数组,从最低位开始取每个位组成radix数组;
步骤3:对radix进行计数排序(利用计数排序适用于小范围数的特点);
10.2 动图演示
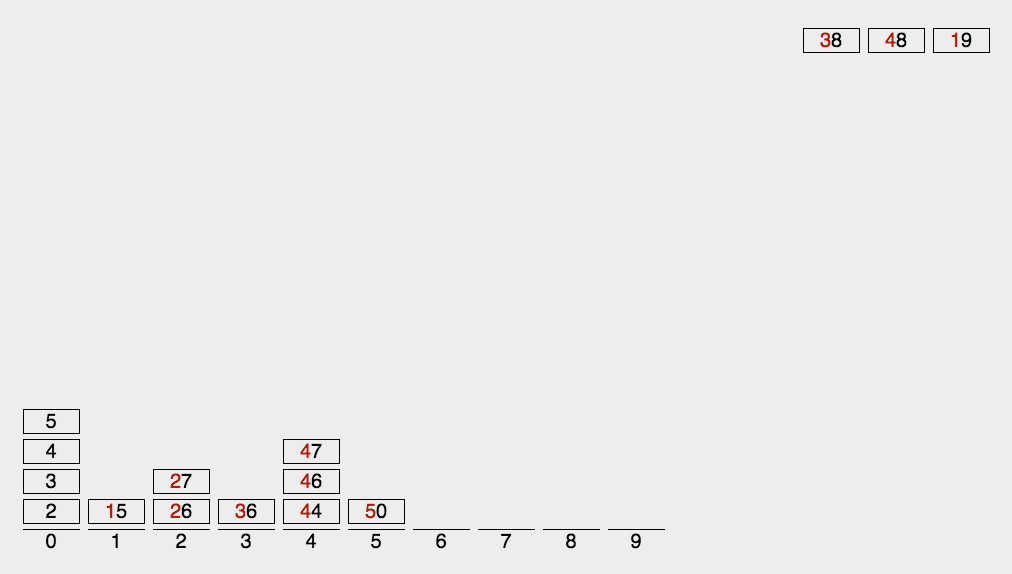
10.3 代码实现
/**
* 基数排序
* @param array
* @return
*/
public static int[] RadixSort(int[] array) {
if (array == null || array.length < 2)
return array;
// 1.先算出最大数的位数;
int max = array[0];
for (int i = 1; i < array.length; i++) {
max = Math.max(max, array[i]);
}
int maxDigit = 0;
while (max != 0) {
max /= 10;
maxDigit++;
}
int mod = 10, div = 1;
ArrayList<ArrayList<Integer>> bucketList = new ArrayList<ArrayList<Integer>>();
for (int i = 0; i < 10; i++)
bucketList.add(new ArrayList<Integer>());
for (int i = 0; i < maxDigit; i++, mod *= 10, div *= 10) {
for (int j = 0; j < array.length; j++) {
int num = (array[j] % mod) / div;
bucketList.get(num).add(array[j]);
}
int index = 0;
for (int j = 0; j < bucketList.size(); j++) {
for (int k = 0; k < bucketList.get(j).size(); k++)
array[index++] = bucketList.get(j).get(k);
bucketList.get(j).clear();
}
}
return array;
}10.4 算法分析
最佳情况:T(n) = O(n * k)
最差情况:T(n) = O(n * k)
平均情况:T(n) = O(n * k)
10.5 基数排序有两种方法:
MSD 从高位开始进行排序
LSD 从低位开始进行排序
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
基数排序: 根据键值的每位数字来分配桶
计数排序: 每个桶只存储单一键值
桶排序: 每个桶存储一定范围的数值
关于JS的十大经典算法和js的十大经典算法有哪些的介绍已经告一段落,感谢您的耐心阅读,如果想了解更多关于Go 之十大经典排序算法、java 十大经典排序算法、java 实现十大经典算法、JAVA十大经典算法总结的相关信息,请在本站寻找。
本文标签:





