如果您想了解Day10Intent部分隐士跳转的相关知识,那么本文是一篇不可错过的文章,我们将为您提供关于16.oauth2+oidc实现client部分、2019wannaflywintercamp
如果您想了解Day10 Intent部分隐士跳转的相关知识,那么本文是一篇不可错过的文章,我们将为您提供关于16.oauth2 + oidc 实现 client部分、2019 wannafly winter camp day1-4代码库、2020 CCPC Wannafly Winter Camp Day1 - I. K 小数查询 (分块)、2020 CCPC Wannafly Winter Camp Day1 Div.1&2总结的有价值的信息。
本文目录一览:- Day10 Intent部分隐士跳转
- 16.oauth2 + oidc 实现 client部分
- 2019 wannafly winter camp day1-4代码库
- 2020 CCPC Wannafly Winter Camp Day1 - I. K 小数查询 (分块)
- 2020 CCPC Wannafly Winter Camp Day1 Div.1&2总结

Day10 Intent部分隐士跳转
游览器
读sd卡
取sd卡

跳转游览器

手机拨号

截图

返回数据的跳转 将得到的视频返回个控件VideoView

判断请求和结果码是否正确 正确做出反应

照相机
需要使用FileProvider 文件提供者 需要在清单文件注册

grantUriPermissions=“true” 可以交互
android:exported=“false”
android:authorities=“com.ghy.1705” 自定义暗号
android:name=“androidx.core.content.FileProvider”> 文件提供者的包名

16.oauth2 + oidc 实现 client部分
把授权和认证过的Server启动一下先
因为代码是之前的代码,所以有些代码需要清除一下
之类注释掉,因为这里暂时没有用到EFCode了

运行的时候发现一点错误
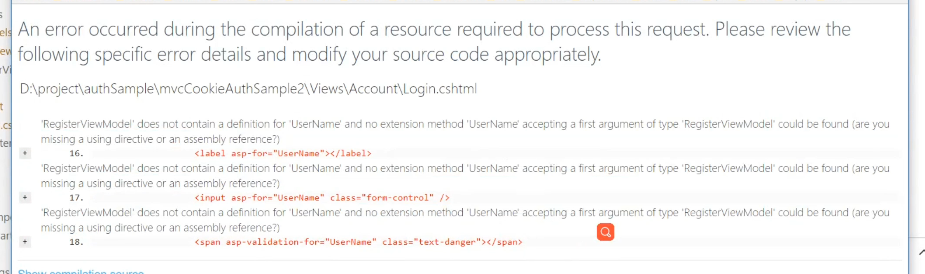
发现登陆的时候使用的RegisterViewModel
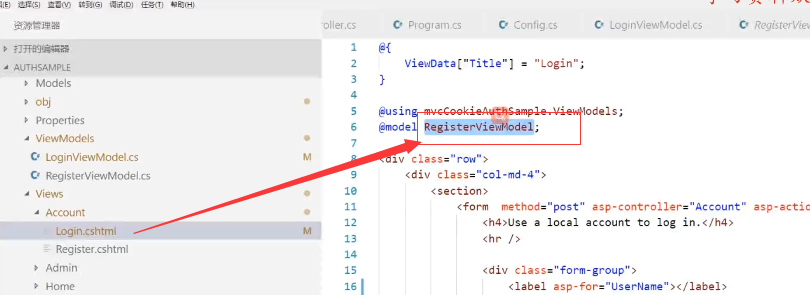
所以这里我们也需要把之前的Email修改为UserName
启动程序

登陆就需要输入这里的用户名和密码

登陆成功,现在是在他本地,

新建客户端,把登陆的信息放到客户端内
新建一个mvc的网站
本身在asp.net core的Authentication认证模块已经内置实现了openIdConnect
所以在这个mvc网站里面不要添加任何第三方的引用,
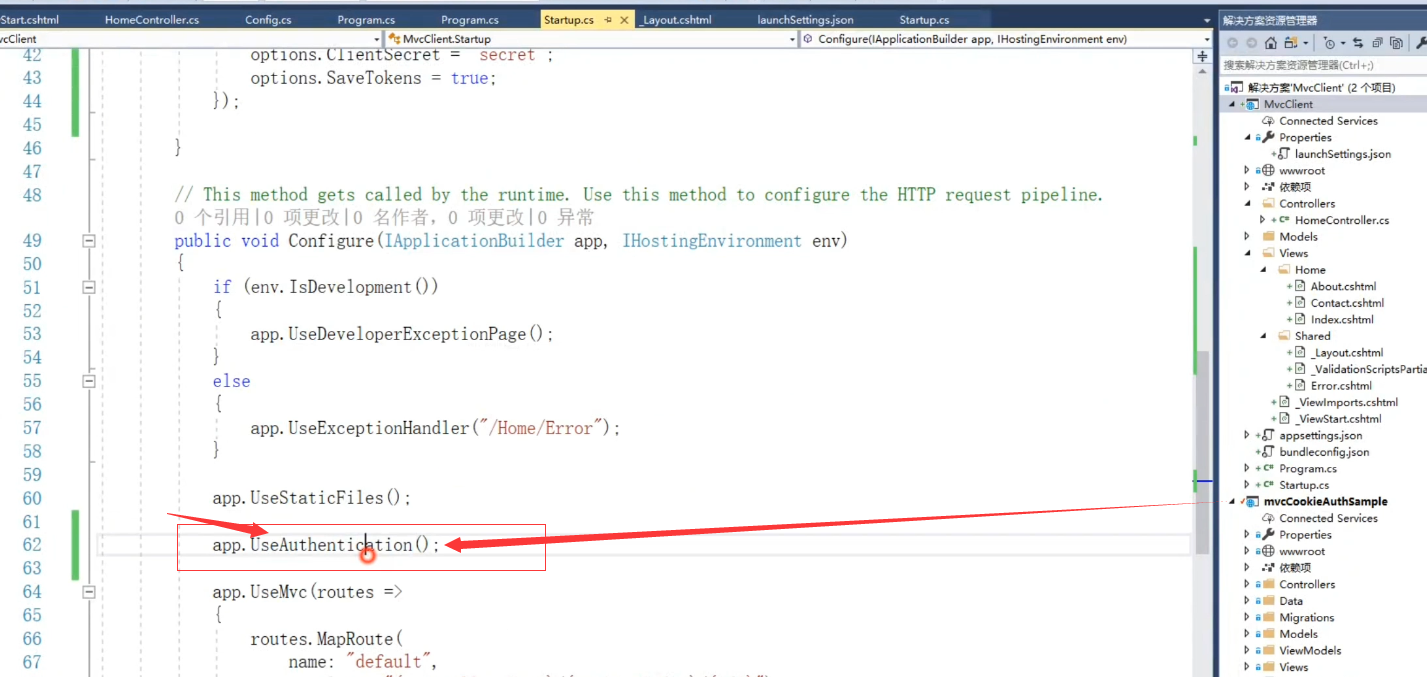
我们唯一要做的就是在这个地方,把Authentication加进来
先添加引用,VScode的只能感知不是很好用,需要先选择一下我们的项目

在命令行 到mvcCient的项目文件夹下 ,然后运行dotnet restore。控制台的终端也需要在我们的项目下

只能感知没有调出来,直接复制完整的引用路径过来。然后切换到VS2017里面
VS2017把这两个项目加进来

mvc的客户端设置为5001启动
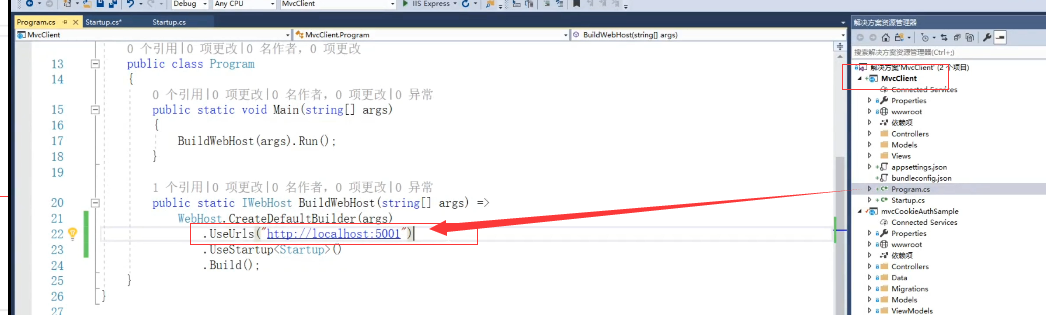 、
、
Server设置为5千来启动
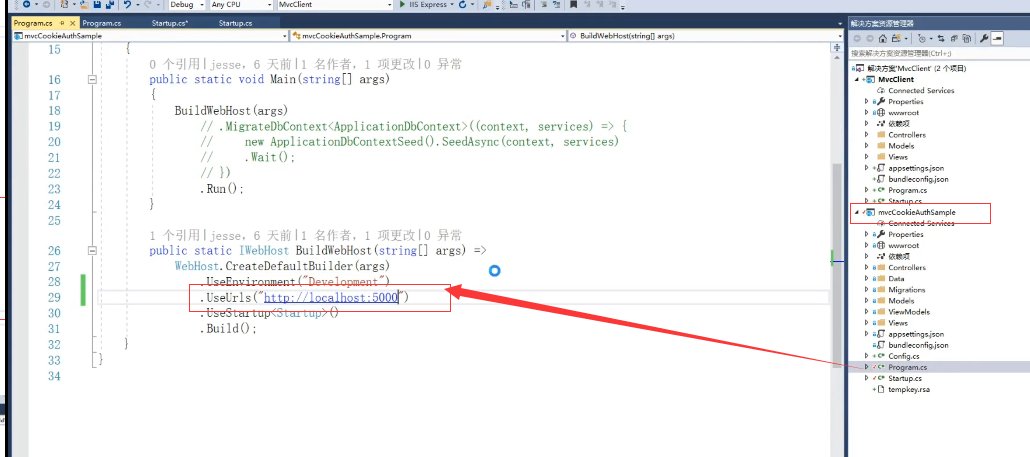
服务端
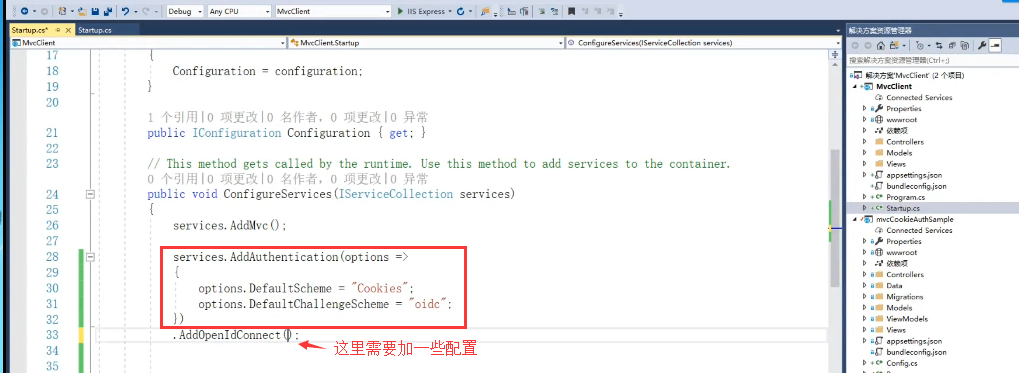
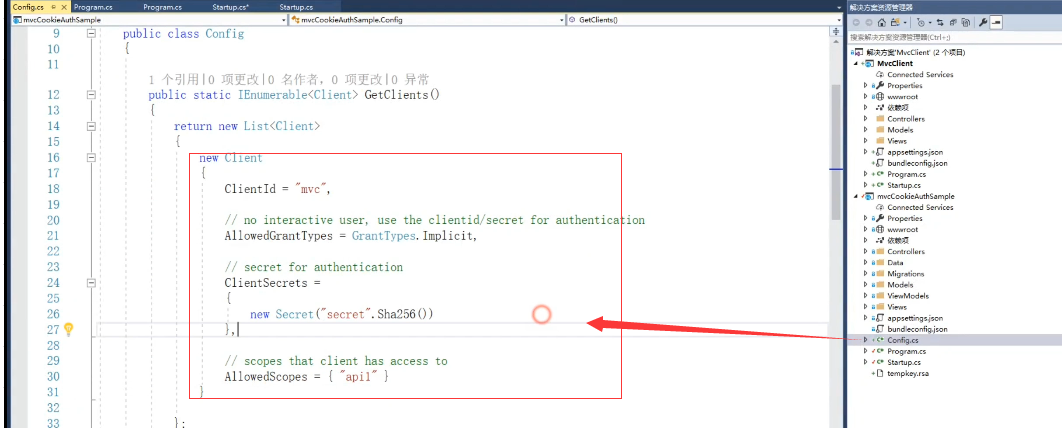
原来这里加了一个Client,如果现在使用OpenIdConnect的话这里需要加一些配置
这个配置就是我们要调转的地址,正常情况下我们是存在数据里的 不是直接改代码的,在asp.net mvc中这个地址的后面的signin-oidc是固定的
这个地址会自动处理登陆的逻辑
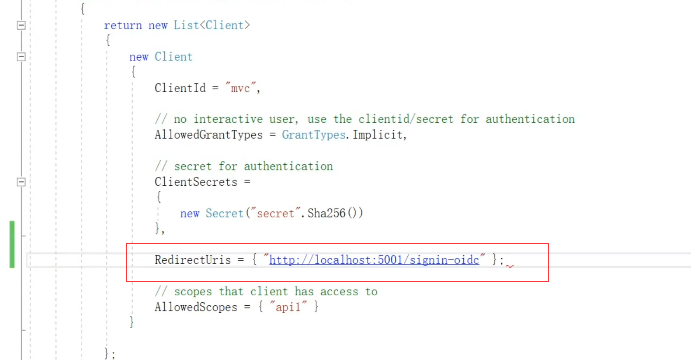
退出返回的地址

在设置Scope

运行服务端
客户端的HomeController设置必须登陆才能访问
客户端也运行起来,客户端启动后报错
客户端把这里也改成5001

这两个地方都要改一下
启动后就成功个跳转了
跳转到 consent这样的一个页面,是要做授权的地方,我们这里没有添加,所以还需要改一个配置

这里我们把Consent设置为false,这个页面就是用于点是否允许授权的页面
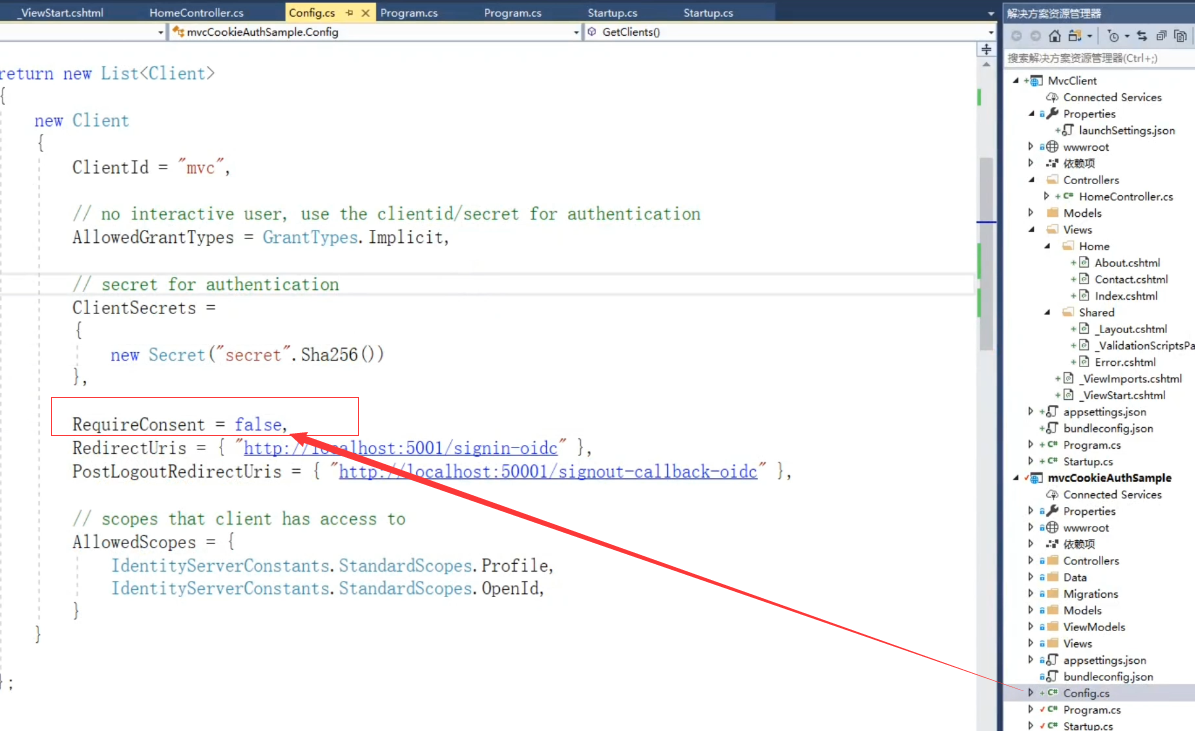
再次运行客户端,因为登陆的cookie已经保存过了 ,所以应该会自动跳转回家去。

成功跳转到了5001的界面。说明我们已经登陆成功了
把这段cookie复制出来看一下
把cookie都删除掉
删除后就会跳转到登陆页面
服务端之前这里没有加上这段代码,现在加上
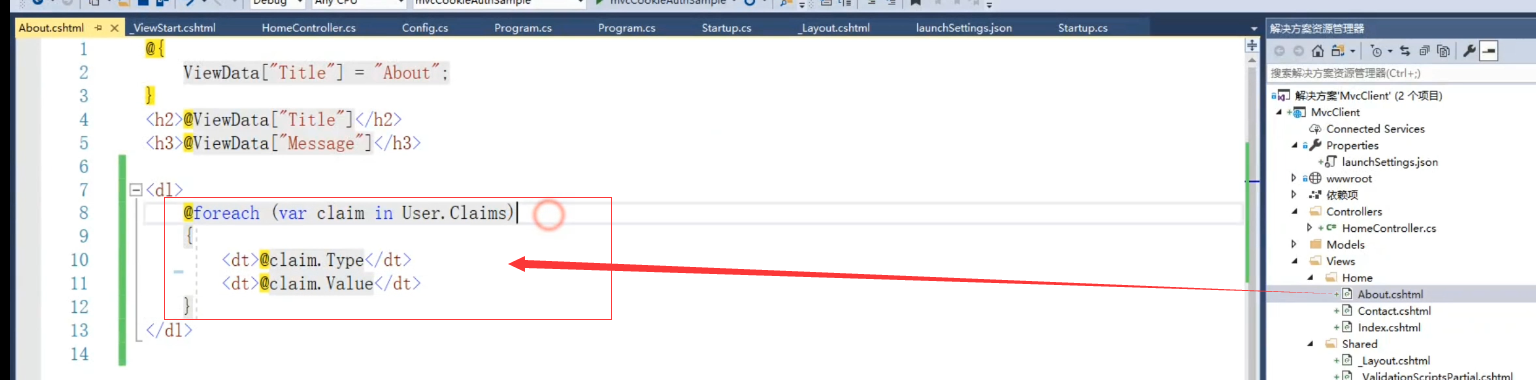
拿到Claims页面后,在客户端显示出来
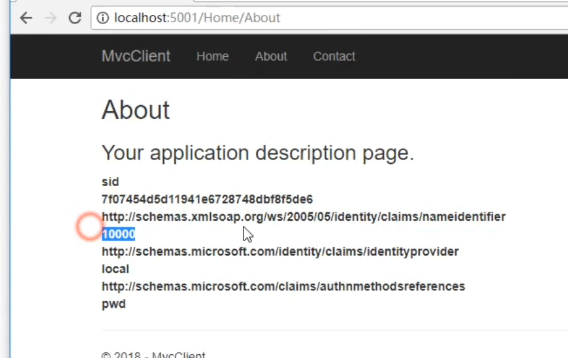
Server端我们返回的是这些信息
因为没有添加ProfileService所以返回的信息有限。接下来会添加 对profile进行补充

2019 wannafly winter camp day1-4代码库
[TOC]
本来是8天代码放一起的,但是太麻烦了,还是分成了2个博客放。
day1
F div1 爬爬爬山 (最短路)
//F
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, LL> pii;
}
using namespace lh;
const int MXN = 1e6 + 7;
const int INF = 0x3f3f3f3f;
const int MOD = 1000000007;
int n, m, k, NODE;
LL height[MXN];
int other[MXN];
vector<pii> mp[MXN];
LL dis[MXN];
struct lp {
int v;
LL w;
friend bool operator <(const lp &a, const lp &b) {
return a.w > b.w;
}
}A, B;
void add_edge(int u,int v,LL w) {
mp[u].push_back({v, w});
}
void dij() {
for(int i = 2; i <= NODE; ++i) dis[i] = 1e18;
dis[1] = 0;
priority_queue<lp> Q;
Q.push({1, 0});
while(!Q.empty()) {
A = Q.top(); Q.pop();
int u = A.v;
if(dis[u] < A.w) continue;
int len = mp[u].size();
for(int i = 0; i < len; ++i) {
int v = mp[u][i].fi;
if(dis[v] > dis[u] + mp[u][i].se) {
dis[v] = dis[u] + mp[u][i].se;
Q.push({v, dis[v]});
}
}
}
printf("%lld\n", dis[n]);
}
int main() {
scanf("%d%d%d", &n, &m, &k);
NODE = n;
for(int i = 1; i <= n; ++i) other[i] = -1;
for(int i = 1; i <= n; ++i) {
scanf("%lld", &height[i]);
if(i > 1 && height[i] - height[1] > k) {
other[i] = ++ NODE;
add_edge(other[i], i, (height[i]-height[1]-k)*(height[i]-height[1]-k));
//add_edge(i, other[i], (height[i]-height[1])*(height[i]-height[1]));
//printf("%d %d\n", i, (height[i]-height[1])*(height[i]-height[1]));
}
}
LL c;
for(int i = 0, a, b; i < m; ++i) {
scanf("%d%d%lld", &a, &b, &c);
if(other[b] == -1) add_edge(a, b, c);
else add_edge(a, other[b], c);
if(other[a] == -1) add_edge(b, a, c);
else add_edge(b, other[a], c);
}
dij();
return 0;
}
B div2 吃豆豆 (dp)
//B
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, LL> pii;
}
using namespace lh;
const int MXN = 1e6 + 7;
const int INF = 0x3f3f3f3f;
const int MOD = 1000000007;
int n, m, C;
int sx,sy,ex,ey;
int ar[15][15];
int dp[15][15][10352];
int dir[5][2]={1,0,0,1,-1,0,0,-1,0,0};
int main() {
scanf("%d%d%d", &n, &m, &C);
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
scanf("%d", &ar[i][j]);
}
}
scanf("%d%d%d%d", &sx, &sy, &ex, &ey);
for(int k = 0; k <= 10351; ++k) {
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
dp[i][j][k] = -INF;
}
}
}
dp[sx][sy][0] = 0;
for(int k = 1; k <= 10351; ++k) {
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
for(int h = 0; h < 5; ++h) {
int px = i + dir[h][0], py = j + dir[h][1];
if(px < 1 || px > n || py < 1 || py > m) continue;
if(dp[px][py][k-1] == -INF) continue;
dp[i][j][k] = max(dp[i][j][k], dp[px][py][k-1]+((k%ar[i][j])==0));
}
}
}
}
int ans = INF;
for(int i = 1; i <= 10351; ++i) {
if(dp[ex][ey][i] >= C) {
ans = i;
break;
}
}
printf("%d\n", ans);
return 0;
}
J div2 夺宝奇兵(暴力)
//J
/*
把所有人宝物从大到小排个序,列出一个柱状图来
枚举其他人最高的宝物的数量为mid,所有高于mid的宝物我们肯定要买的
如果这时获得宝物已经多于mid了,就可以return了
不然就从剩下所有的宝物里面选出价值最小的几个宝物凑出mid+1个宝物出来
*/
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, LL> pii;
}
using namespace lh;
const LL INF = 1e18;
const int N = 1e4 + 100;
vector<LL> c[N];
int n, m;
LL x;
LL solve(int mid){
LL tmp = 0;
int now = 0;
std::vector<LL> vs;
for(int i = 2; i <= n; ++i) {
int siz = c[i].size();
if(siz >= mid) {
for(int j = 0; j < siz - mid; ++j) tmp += c[i][j], now++;
for(int j = siz - mid; j < siz; ++j) vs.push_back(c[i][j]);
}else {
for(int j = 0; j < siz; ++j) vs.push_back(c[i][j]);
}
}
if(now > mid) return tmp;
if(now + vs.size() <= mid) return INF;
sort(vs.begin(), vs.end());
for(int i = 0; i <= mid - now && i < vs.size(); ++i) {
tmp += vs[i];
}
return tmp;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, ar; i <= m; ++i){
scanf("%lld%d", &x, &ar);
++ ar; c[ar].pb(x);
}
++ n;
for (int i = 2; i <= n; ++i){
sort(c[i].begin(), c[i].end());
}
LL tmp = 1e18;
for (int i = 1; i <= m; ++i){
tmp = min(tmp, solve(i));
}
printf("%lld\n", tmp);
return 0;
}
J div1 夺宝奇兵 (权值线段树)
//太菜了,后缀和都不会写了,找了一万年的bug
#include<bits/stdc++.h>
#define fi first
#define se second
#define lson rt<<1
#define rson rt<<1|1
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
}
using namespace lh;
const LL INF = 1e18;
const int MXN = 4e5 + 7;
int n, m;
std::vector<int> shut[MXN];
std::vector<pii > mp[MXN];
pii ar[MXN];
LL suf[MXN], SUM[MXN<<2];
int num[MXN], NUM[MXN<<2];
LL min_sum;
int min_num;
bool cmp(const pii &a, const pii &b) {
if(a.fi != b.fi) return a.fi > b.fi;
return a.se > b.se;
}
void push_up(int rt) {
NUM[rt] = NUM[lson] + NUM[rson];
SUM[rt] = SUM[lson] + SUM[rson];
}
void build(int l,int r,int rt) {
if(l == r) {
NUM[rt] = 1;
SUM[rt] = ar[l].fi;
return ;
}
int mid = (l + r) >> 1;
build(l, mid, lson), build(mid+1, r, rson);
push_up(rt);
}
void update(int p, int v, int l, int r, int rt) {
if(l == r) {
NUM[rt] = 0;
SUM[rt] = 0;
return ;
}
int mid = (l + r) >> 1;
if(p <= mid) update(p, v, l, mid, lson);
else update(p, v, mid+1, r, rson);
push_up(rt);
}
LL query(int nd, int l, int r, int rt) {
//printf("%d %d %d %d %lld\n", nd, l, r, NUM[rt], SUM[rt]);
if(l == r || nd == NUM[rt]) {
return SUM[rt];
}
int mid = (l + r) >> 1;
if(NUM[lson] >= nd) return query(nd, l, mid, lson);
else {
return SUM[lson] + query(nd - NUM[lson], mid+1, r, rson);
}
}
LL solve(int mid) {
LL ans = min_sum;//min_sum 和 suf[mid+1]
if(min_num > mid) return ans;//min_num 和 num[mid+1]
if(NUM[1] + min_num <= mid) return INF;
int nd = min(mid + 1 - min_num, NUM[1]);
ans += query(nd, 1, m, 1);
return ans;
}
int main() {
scanf("%d%d", &n, &m);
int x, a;
LL ans = 0;
for(int i = 1; i <= m; ++i) {
scanf("%d%d", &x, &a);
ar[i] = {x, a};
ans = ans + x;
}
sort(ar + 1, ar + 1 + m);
for(int i = 1; i <= m; ++i) {
mp[ar[i].se].push_back({ar[i].fi, i});
}
build(1, m, 1);
for(int i = 1; i <= n; ++i) {
sort(mp[i].begin(), mp[i].end(), cmp);
for(int j = mp[i].size(); j >= 1; --j) {
shut[j].push_back(mp[i][j-1].se);
}
}
//printf("[%lld]\n", query(4, 1, m, 1));
for(int i = m; i >= 1; --i) {
ans = min(ans, solve(i));
for(auto x: shut[i]) {
++ min_num;
min_sum += ar[x].fi;
update(x, -1, 1, m, 1);
}
}
printf("%lld\n", ans);
return 0;
}
C div1 拆拆拆数
#include<bits/stdc++.h>
#define fi first
#define se second
#define lson rt<<1
#define rson rt<<1|1
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
}
using namespace lh;
const int MXN = 4e5 + 7;
//一个偶数可以拆成一个奇数和一个奇素数之和
int n, m;
LL a, b;
LL pp[20] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59};
LL gcd(LL a, LL b) {
return b==0?a:gcd(b,a%b);
}
int main() {
scanf("%d", &n);
m = 17;
while(n --) {
scanf("%lld%lld", &a, &b);
if(gcd(a, b) == 1) {
printf("1\n%lld %lld\n", a, b);
continue ;
}
int flag = 0;
if(b % 2 == 0) swap(a, b), flag = 1;
if(a % 2 == 0) {
for(int i = 0; i < m; ++i) {
if(gcd(b-2, pp[i]) == 1 && gcd(a-pp[i],2) == 1) {
if(flag == 0) printf("2\n%lld %lld\n%lld %lld\n",pp[i],b-2,a-pp[i],2LL);
else printf("2\n%lld %lld\n%lld %lld\n",b-2,pp[i],2LL,a-pp[i]);
break;
}
}
}else {
if(flag == 0) printf("2\n%lld %lld\n%lld %lld\n", 2LL, b-2, a-2, 2LL);
else printf("2\n%lld %lld\n%lld %lld\n", b-2, 2LL, 2LL, a-2);
}
}
return 0;
}
//这个也行
using namespace lh;
const int MXN = 4e5 + 7;
int n, m;
LL a, b;
LL pp[20] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59};
LL gcd(LL a, LL b) {
return b==0?a:gcd(b,a%b);
}
int main() {
#ifndef ONLINE_JUDGE
freopen("E://ADpan//in.in", "r", stdin);
//freopen("E://ADpan//out.out", "w", stdout);
#endif
scanf("%d", &n);
m = 17;
while(n --) {
scanf("%lld%lld", &a, &b);
if(gcd(a, b) == 1) {
printf("1\n%lld %lld\n", a, b);
continue ;
}else if(a % 2 == 1 && b % 2 == 1) {
printf("2\n%lld %lld\n%lld %lld\n", 2LL, b-2, a-2, 2LL);
continue;
}
printf("2\n");
int flag = 1;
for(LL i = 2; i <= 100 && flag; ++i) {
for(LL j = 2; j <= 100 && flag; ++j) {
if(gcd(i,j) == 1 && gcd(a-i,b-j) == 1) {
printf("%lld %lld\n%lld %lld\n", i,j,a-i,b-j);
flag = 0;
}else if(gcd(i,b-j) == 1 && gcd(a-i,j) == 1) {
flag = 0;
printf("%lld %lld\n%lld %lld\n", i,b-j,a-i,j);
}
}
}
}
return 0;
}
E div1 流流流动(冰雹猜想 ,树形dp)
//这玩意会连成一个森林
#include<bits/stdc++.h>
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
}
using namespace lh;
const int MXN = 4e5 + 7;
int n, m;
std::vector<int> son[MXN];
int f[MXN], d[MXN], vis[MXN];
LL dp[MXN][2];
//dp[i][0]表示不选i, dp[i][1]表示选i
void dfs(int u,int ba) {
dp[u][1] += f[u];
vis[u] = 1;
for(auto v: son[u]) {
if(v == ba) continue;
dfs(v, u);
dp[u][0] += max(dp[v][0], dp[v][1]);
dp[u][1] += max(dp[v][0], dp[v][1]-d[min(u, v)]);
}
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%d", &f[i]);
for(int i = 1; i <= n; ++i) scanf("%d", &d[i]);
for(int i = 2; i <= n; ++i) {
if(i % 2 == 0) {
son[i].push_back(i/2);
son[i/2].push_back(i);
}else if(i*3+1 <= n){
son[i].push_back(i*3+1);
son[i*3+1].push_back(i);
}
}
LL ans = 0;
for(int i = 1; i <= n; ++i) {
if(vis[i] == 0) {
dfs(i, i);
ans += max(dp[i][0], dp[i][1]);
}
}
printf("%lld\n", ans);
return 0;
}
I div2 起起落落 (dp)
$dp[i]=\sum_{j=1}^{j<i}[p[j]>p[i]]\times dp[j]\times \sum_{h=j+1}^{h<i}[p[h]<p[j]]$
/*
题意:
给你一个长度为n的排列,问有多少个长度为(2*m+1)奇数且大于3的子序列满足一下条件:
1.下标序列递增(这个没啥重要的
2.(1<=i<=m) p[2*i-1]>p[2*i+1]>p[2*i]
dp[i]表示以i结尾符合条件的序列的个数
dp[i]=\sum_{j=1}^{j<i}[p[j]>p[i]]\times dp[j]\times \sum_{h=j+1}^{h<i}[p[h]<p[j]]
这种转移方法构造出来的方案中序列的长度肯定是奇数的
*/
#include<bits/stdc++.h>
#define fi first
#define se second
#define lson rt<<1
#define rson rt<<1|1
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
}
using namespace lh;
const int mod = 1e9 +7;
const int MXN = 4e5 + 7;
int n, m;
int p[MXN];
LL dp[MXN], suf[MXN];
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%d", &p[i]);
LL ans = 0;
for(int i = 3, cnt; i <= n; ++i) {
cnt = 0;
for(int j = i-1; j >= 1; --j) {
if(p[j] < p[i]) {
++ cnt;
continue;
}
dp[i] = (dp[i]+ (1+dp[j])*cnt%mod) % mod;//加1是要加上取单独j这一个元素和cnt和i相组合的情况
}
if(i >= 3) ans = (ans + dp[i]) % mod;
}
printf("%lld\n", ans);
return 0;
}
I div1 起起落落 (权值线段树优化dp)
待填坑
day2
A div2 Erase Nodes(贪心)
//A
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef unsigned long long LL;
typedef pair<int, LL> pii;
}
using namespace lh;
const int MXN = 1e4 + 100;
int n;
int ar[MXN];
LL dp[20];
int get(int x) {
int num = 0;
while(x) {
num ++;
x /= 10;
}
return num;
}
int main() {
dp[0] = 1;
for(int i = 1; i <= 10; ++i) {
dp[i] = dp[i-1] * 10;
}
int cas = 0;
int tim; scanf("%d", &tim);
while(tim --) {
scanf("%d", &n);
int cnt = 0;
for(int i = 1; i <= n; ++i) {
scanf("%d", &ar[i]);
if(ar[i] == 1000000000) cnt++;
}
int mmax = ar[n], wei = get(ar[n]);
LL ans = 0, tmp = 0;
int flag = 0;
for(int i = n-1; i >= 1; --i) {
ans = ar[i];
ans *= dp[wei];
ans += mmax;
tmp = max(tmp, ans);
if(ar[i] > mmax) {
mmax = ar[i];
wei = get(ar[i]);
}
}
printf("Case #%d: %llu\n", ++cas, tmp);
}
return 0;
}
B div2 Erase Numbers III(贪心)
//B
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef unsigned long long LL;
typedef pair<int, LL> pii;
}
using namespace lh;
const int INF = 0x3f3f3f3f;
const int MXN = 1e4 + 100;
int n;
int ar[MXN], len[MXN], br[MXN], is[MXN], len2[MXN], id[MXN];
LL dp[20];
int get(int x) {
int num = 0;
while(x) {
num ++;
x /= 10;
}
return num;
}
string toString(int x) {
string ans;
char c;
while(x) {
c = x%10+''0'';
ans = c + ans;
x /= 10;
}
return ans;
}
int A[20], B[20];
bool mycmp(int x, int y) {//x是否比y字典序小
A[0] = B[0] = 0;
while(x) {
A[++A[0]] = x%10;
x /= 10;
}
while(y) {
B[++B[0]] = y%10;
y /= 10;
}
reverse(A+1, A+A[0]+1);
reverse(B+1, B+B[0]+1);
int tmp = min(A[0], B[0]);
for(int i = 1; i <= tmp; ++i) {
if(A[i] > B[i]) return 0;
else if(A[i] < B[i]) return 1;
}
return 1;
}
int main() {
int cas = 0;
int tim; scanf("%d", &tim);
while(tim --) {
scanf("%d", &n);
int mmin = INF;
for(int i = 1; i <= n; ++i) is[i] = 0;
for(int i = 1; i <= n; ++i) {
scanf("%d", &ar[i]);
len[i] = get(ar[i]);
br[i] = len[i];
mmin = min(mmin, len[i]);
}
sort(br + 1, br + 1 + n);
int flag = 0;
if(br[1] == br[2]) flag = 1;
printf("Case #%d: ", ++cas);
int pos = -1;
if(flag == 1) {
std::vector<int> my;
for(int i = 1; i < n; ++i) {
if(len[i] == mmin && mycmp(ar[i], ar[i+1])) {
my.push_back(i);
is[i] = 1;
//printf("*%d\n", i);
break;
}
}
int cnt2 = 0;
for(int i = 1; i <= n; ++i) {
if(is[i] == 0) br[++cnt2] = ar[i], len2[cnt2] = len[i], id[cnt2] = i;
}
for(int i = 1; i < cnt2; ++i) {
if(len2[i] == mmin && mycmp(br[i], br[i+1])) {
my.push_back(id[i]);
is[id[i]] = 1;
//printf("**%d\n", id[i]);
break;
}
}
for(int i = n; i >= 1 && my.size() < 2; --i) {
if(is[i] == 0 && len[i] == mmin) my.push_back(i);
}
string ans1, ans2;
for(int i = 1; i <= n; ++i) {
if(i == my[0] || i == my[1]) continue;
ans1 += toString(ar[i]);
}
//cout<<ans1<<"\n";
my.clear();
for(int i = 1; i + 2 <= n; ++i) {
if(len[i] + len[i+1] == mmin + mmin) {
if(mycmp(ar[i], ar[i+2])) {
my.push_back(i);
break;
}
}
}
int hh = 0;
if(my.size() == 0) {
for(int i = n; i >= 2; --i) {
if(len[i] + len[i-1] == mmin + mmin) {
my.push_back(i);
break;
}
}
if(my.size() == 1) {
hh = 1;
my.push_back(my[0]-1);
for(int i = 1; i <= n; ++i) {
if(i == my[0] || i == my[1]) continue;
ans2 += toString(ar[i]);
}
}
}
if(hh) ans1 = max(ans1, ans2);
cout<<ans1<<"\n";
continue;
}
pos = -1;
int fuck = br[2];
for(int i = 1, nex; i < n; ++i) {
nex = ar[i+1];
if(len[i+1] == mmin && i + 2 <= n) nex = ar[i+2];
if(len[i] == fuck) {
if(mycmp(ar[i], nex)) {
pos = i;
break;
}
}
}
if(pos == -1) {
for(int i = n; i >= 1; --i) {
if(len[i] == mmin) continue;
if(len[i] != fuck) continue;
pos = i;
break;
}
}
for(int i = 1; i <= n; ++i) {
if(i == pos || len[i] == mmin) {
}else printf("%d", ar[i]);
}
printf("\n");
}
return 0;
}//求ac
H div1&2 Cosmic Cleaner(计算几何)
球缺体积 用一个平面截去一个球所得部分叫球缺 球缺面积$=2\times πh$ 球缺体积$=π\times h^2\times (R−\frac{h}{3})$ 球缺质心:匀质球缺的质心位于它的中轴线上,并且与底面的距离为 $C=\frac{(4R-h)\times h}{12R-4h}=\frac{(d^2+2h^2)\times h}{3d^2+4h^2}$ 其中,$h$为球缺的高,$R$为大圆半径,$d$为球缺的底面直径 https://blog.csdn.net/enterprise_/article/details/81624174 https://paste.ubuntu.com/p/5qZKXYFsjQ/
//H
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef unsigned long long LL;
typedef pair<int, LL> pii;
}
using namespace lh;
const int INF = 0x3f3f3f3f;
const double pi = acos(-1.0);
const int MXN = 1e4 + 100;
int n;
int A, B, C, r1;
struct lp {
int a, b, c, r2;
}cw[MXN];
double tiji(lp ar) {
double d = sqrt(o2(ar.a-A)+o2(ar.b-B)+o2(ar.c-C));
double r2 = ar.r2;
double X = r1-(r1*r1-r2*r2+d*d)/(2*d);
double Y = r2-(r2*r2-r1*r1+d*d)/(2*d);
double ans = pi/3*X*X*(3*r1-X)+pi/3*Y*Y*(3*r2-Y);
return ans;
}
int main() {
int cas = 0;
int tim; scanf("%d", &tim);
while(tim --) {
scanf("%d", &n);
int a, b, c, r2;
double d;
for(int i = 1; i <= n; ++i) {
scanf("%d%d%d%d", &a, &b, &c, &r2);
cw[i] = {a, b, c, r2};
}
scanf("%d%d%d%d", &A, &B, &C, &r1);
double ans = 0;
for(int i = 1; i <= n; ++i) {
double d = sqrt(o2(cw[i].a-A)+o2(cw[i].b-B)+o2(cw[i].c-C));
if(d > r1 + cw[i].r2) continue;
if(d + cw[i].r2 <= r1) {
ans += 4.0*pi/3*cw[i].r2*cw[i].r2*cw[i].r2;
}else ans += tiji(cw[i]);
}
printf("Case #%d: %.10f\n", ++cas, ans);
}
return 0;
}
/*X = r1-(r1^2-r2^2+d^2)/2d
pi/3*(X)^2*(3r1-(X))
Y = r2-(r2^2-r1^2+d^2)/2d
+pi/3*(Y)^2*(3r2-(Y))*/
K div1 Sticks 搜索
//12分6写的有点丑https://paste.ubuntu.com/p/kHBHNCGgnh/
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
}
using namespace lh;
const int INF = 0x3f3f3f3f;
const int MXN = 1e4 + 100;
int n;
LL ar[MXN];
int is[13][13][13], g[13];
struct lp {
LL x, y, z;
}ans[5], tmp[5];
int ANS;
void dfs(int cur, int num) {
if(cur/3 + num <= ANS) return ;
if(cur == 3) {
if(ar[g[0]]+ar[g[1]] > ar[g[2]]) {
num ++;
tmp[num].x = ar[g[0]]; tmp[num].y = ar[g[1]]; tmp[num].z = ar[g[2]];
}
if(num > ANS) {
ANS = num;
for(int i = 1; i <= num; ++i) ans[i] = tmp[i];
}
return ;
}
int d[13];
for(int i = 0; i < cur; ++i) d[i] = g[i];
int k = 0, ret;
//tmp[num+1].x = ar[d[0]];
for(int i = 1; i < cur; ++i) {
//tmp[num+1].y = ar[d[i]];
for(int j = i + 1; j < cur; ++j) {
//tmp[num+1].z = ar[d[j]];
ret = num + is[d[0]][d[i]][d[j]];
if(is[d[0]][d[i]][d[j]]) {
tmp[num+1].x = ar[d[0]];
tmp[num+1].y = ar[d[i]];
tmp[num+1].z = ar[d[j]];
}
k = 0;
for(int t = 1; t < cur; ++t) {
if(t != i && t != j) g[k++] = d[t];
}
dfs(cur-3, ret);
if(ANS == 4) return ;
}
}
}
int main() {
int cas = 0;
int tim; scanf("%d", &tim);
while(tim --) {
for(int i = 0; i < 12; ++i) scanf("%lld", &ar[i]), g[i] = i;
sort(ar, ar + 12);
for(int i = 0; i < 12; ++i) {
for(int j = i + 1; j < 12; ++j) {
for(int k = j + 1; k < 12; ++k) {
is[i][j][k] = ((ar[i] + ar[j]) > ar[k]);
}
}
}
ANS = 0;
dfs(12, 0);
printf("Case #%d: %d\n", ++cas, ANS);
for(int i = 1; i <= ANS; ++i) {
printf("%lld %lld %lld\n", ans[i].x, ans[i].y, ans[i].z);
}
}
return 0;
}
day3
F div2 小清新数论(莫比乌斯反演)
莫比乌斯反演
//F
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MXN = 1e7+ 7;
const int mod = 998244353;
LL n, m;
int noprime[MXN], pp[MXN], pcnt;
int phi[MXN], mu[MXN];
LL pre_mu[MXN];
void init_prime() {
noprime[0] = noprime[1] = 1;
mu[1] = 1; phi[1] = 1;
for(int i = 2; i < MXN; ++i) {
if(!noprime[i]) pp[pcnt++] = i, phi[i] = i-1, mu[i] = -1;
for(int j = 0; j < pcnt && pp[j] * i < MXN; ++j) {
noprime[pp[j]*i] = 1;
phi[pp[j]*i] = (pp[j]-1)*phi[i];
mu[pp[j]*i] = -mu[i];
if(i % pp[j] == 0) {
phi[pp[j]*i] = pp[j]*phi[i];
mu[pp[j]*i] = 0;
break;
}
}
}
for(int i = 1; i < MXN; ++i) pre_mu[i] = pre_mu[i-1] + mu[i];
}
LL solve(LL n) {
LL ans = 0, tmp;
for(LL L = 1, R; L <= n; L = R + 1) {
R = n/(n/L);
tmp = pre_mu[R]-pre_mu[L-1];
ans = (ans + tmp*(n/L)%mod*(n/L)%mod)%mod;
}
return (ans+mod)%mod;
}
int main() {
init_prime();
scanf("%lld", &n);
LL ans = 0, tmp;
for(LL L = 1, R; L <= n; L = R + 1) {
R = n/(n/L);
tmp = pre_mu[R]-pre_mu[L-1];
ans = (ans + tmp*solve(n/L)%mod)%mod;
}
printf("%lld\n", (ans+mod)%mod);
return 0;
}
F div1 小清新数论(杜教筛)
杜教筛 题解 code1:利用欧拉函数
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MXN = 1e7+ 7;
const LL mod = 998244353;
const LL inf = 1e18;
LL n, m, inv2;
int noprime[MXN], pp[MXN], pcnt;
int phi[MXN], mu[MXN];
LL pre_mu[MXN], pre_phi[MXN];
unordered_map<LL, LL> mp1, mp2;
void init_prime() {
noprime[0] = noprime[1] = 1;
mu[1] = 1; phi[1] = 1;
for(int i = 2; i < MXN; ++i) {
if(!noprime[i]) pp[pcnt++] = i, phi[i] = i-1, mu[i] = -1;
for(int j = 0; j < pcnt && pp[j] * i < MXN; ++j) {
noprime[pp[j]*i] = 1;
phi[pp[j]*i] = (pp[j]-1)*phi[i];
mu[pp[j]*i] = -mu[i];
if(i % pp[j] == 0) {
phi[pp[j]*i] = pp[j]*phi[i];
mu[pp[j]*i] = 0;
break;
}
}
}
for(int i = 1; i < MXN; ++i) {
pre_mu[i] = pre_mu[i-1] + mu[i];
pre_phi[i] = (pre_phi[i-1] + phi[i])%mod;
}
}
LL solve_mu(LL n) {
if(n < MXN) return pre_mu[n];
if(mp1[n] == inf) return 0;
if(mp1[n]) return mp1[n];
LL ans = 1;
for(LL L = 2, R; L <= n; L = R + 1) {
R = n/(n/L);
ans -= (R-L+1LL)%mod*solve_mu(n/L);
}
mp1[n] = ans;
if(mp1[n] == 0) mp1[n] = inf;
return ans;
}
LL solve_phi(LL n) {
if(n < MXN) return pre_phi[n];
if(mp2[n]) return mp2[n];
LL ans = n%mod*(n+1)%mod*inv2%mod;
for(LL L = 2, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans - (R-L+1LL)%mod*solve_phi(n/L)%mod)%mod;
}
ans = (ans + mod) % mod;
mp2[n] = ans;
return ans;
}
int main() {
inv2 = 499122177;
init_prime();
scanf("%lld", &n);
LL ans = 0;
for(LL L = 1, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans + (solve_mu(R)-solve_mu(L-1))%mod*(solve_phi(n/L)*2LL%mod-1LL)%mod+mod)%mod;
}
printf("%lld\n", (ans+mod)%mod);
return 0;
}
code2:利用莫比乌斯反演和迪利克雷卷积
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false);cin.tie(0)
#define pb push_back
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
typedef pair<LL, LL> pll;
const int INF = 0x3f3f3f3f;
const LL MOD = 998244353;
const int MXN = 5e6 + 6;
LL n, q, m;
int noprime[MXN], pp[MXN/2], pcnt;
int mu[MXN], phi[MXN];
int pre_mu[MXN];
LL mumu[MXN];
unordered_map<LL,LL>mp1,mp2;
void init_rime() {
noprime[0] = noprime[1] = 1;
mu[1] = 1;
for(int i = 2; i < MXN; ++i) {
if(!noprime[i]) pp[pcnt++] = i, mu[i]=-1;
for(int j = 0; j < pcnt && i*pp[j] < MXN; ++j) {
noprime[i*pp[j]] = 1;
mu[i*pp[j]] = -mu[i];
if(i % pp[j] == 0) {
mu[i*pp[j]] = 0;
break;
}
}
}
for(int i = 1; i < MXN; ++i) pre_mu[i] = pre_mu[i-1] + mu[i], mumu[i] = mu[i];
for(int i = 2; i < MXN; ++i) {
for(int j = i; j < MXN; j += i) {
mumu[j] += mu[i]*mu[j/i];
if(mumu[j] >= MOD) mumu[j] %= MOD;
}
}
for(int i = 2; i < MXN; ++i) mumu[i] = (mumu[i]+mumu[i-1]+MOD)%MOD;
}
LL solve_u(LL n) {
if(n < MXN) return pre_mu[n];
if(mp1.count(n)) return mp1[n];
LL ans = 1;
for(LL L = 2, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans - (R-L+1)%MOD*solve_u(n/L)%MOD+MOD)%MOD;
}
mp1[n] = ans;
return ans;
}
LL solve_uu(LL n) {
if(n < MXN) return mumu[n];
if(mp2.count(n)) return mp2[n];
LL ans = 0;
for(LL L = 1, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans + (solve_u(R)-solve_u(L-1)+MOD)%MOD*solve_u(n/L)%MOD);
if(ans >= MOD) ans %= MOD;
}
mp2[n] = (ans+MOD)%MOD;
return ans;
}
int main(int argc, char const *argv[]) {
init_rime();
scanf("%lld", &n);
LL ans = 0;
for(LL L = 1, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans + (n/L)%MOD*(n/L)%MOD*(solve_uu(R)-solve_uu(L-1)+MOD)%MOD)%MOD;
}
printf("%lld\n", (ans+MOD)%MOD);
return 0;
}
/*
void init_rime() {
noprime[0] = noprime[1] = 1;
mu[1] = 1;mumu[1] = 1;
for(int i = 2; i < MXN; ++i) {
if(!noprime[i]) pp[pcnt++] = i, mu[i]=-1, mumu[i]=-2;
for(int j = 0; j < pcnt && i*pp[j] < MXN; ++j) {
noprime[i*pp[j]] = 1;
mu[i*pp[j]] = -mu[i];
mumu[i*pp[j]] = mumu[i]*mumu[pp[j]];
if(i % pp[j] == 0) {
mu[i*pp[j]] = 0;
if((i/pp[j])%pp[j]) mumu[i*pp[j]] = mumu[i/pp[j]];
else mumu[i*pp[j]] = 0;
break;
}
}
}
for(int i = 1; i < MXN; ++i) pre_mu[i] = pre_mu[i-1] + mu[i];
for(int i = 2; i < MXN; ++i) mumu[i] = (mumu[i]+mumu[i-1]+MOD)%MOD;
}
*/
H div2 涂鸦(计数)
//H
#include<bits/stdc++.h>
#define fi first
#define se second
#define lson rt<<1
#define rson rt<<1|1
#define iis std::ios::sync_with_stdio(false)
#define pb push_back
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, LL> pii;
}
using namespace lh;
const int mod = 998244353;
const int INF = 0x3f3f3f3f;
const int MXN = 2e5 + 7;
const int N = 1e3 + 7;
int n, m;
int ar[N][N];
LL dp[1005][1005];
LL ksm(LL a, LL b) {
LL res = 1;
while(b) {
if(b & 1) res = res *a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
int da[N][N], di[N][N], dj[N][N],dij[N][N];
void ADD(LL &a) {
if(a >= mod) a %= mod;
}
int lowbit(int x) {
return x&(-x);
}
//sumxy = (x+1)(y+1)sigma(d[i][j])-(y+1)sigma(i*d[i][j])-(x+1)sigma(j*d[i][j])+sigma(i*j*d[i][j])
void add(int x, int y, int z){
for(int i=x;i<=n;i+=lowbit(i)){
for(int j=y;j<=m;j+=lowbit(j)){
da[i][j] += z; di[i][j] += z*x; dj[i][j] += z*y; dij[i][j] += z*x*y;
}
}
}
void update(int xa,int ya,int xb,int yb,int z){
add(xa,ya,z);add(xa,yb+1,-z);add(xb+1,ya,-z);add(xb+1,yb+1,z);
}
int query(int x, int y){
int res = 0;
for(int i = x; i>0; i -= lowbit(i)){
for(int j = y; j>0; j -= lowbit(j)){
res += (x+1)*(y+1)*da[i][j] - (y+1)*di[i][j] - (x+1)*dj[i][j] + dij[i][j];
}
}
return res;
}
int ask(int xa,int ya,int xb,int yb){
return query(xb,yb)-query(xb,ya-1)-query(xa-1,yb)+query(xa-1,ya-1);
}
void init(){
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
LL tmp = dp[i][j]-dp[i-1][j]-dp[i][j-1]+dp[i-1][j-1];
tmp = (tmp%mod + mod)%mod;
add(i,j,tmp);
}
}
}
int main(int argc, char const *argv[]) {
int q;
scanf("%d%d%d", &n, &m, &q);
LL tmp, l, r;
LL two = ksm(2, mod-2);
for(int i = 1; i <= n; ++i) {
scanf("%lld%lld", &l, &r);
tmp = (r-l+1)*(r-l+2)%mod;
tmp = ksm(tmp, mod - 2);
for(int j = l; j <= r; ++j) {
dp[i][j] = (j-l+1)*(r-j+1)%mod*tmp%mod*2%mod;
}
}
LL ANS = 0;
//init();
//printf("%lld %d\n", ANS, ask(1, 1, n, m));
int x1, y1, x2, y2;
while(q--) {
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
if(x1+y1 > x2+y2) {
swap(x1,x2);
swap(y1,y2);
}
//printf("%d %d %d %d\n", x1,y1,x2,y2);
update(x1,y1,x2,y2,1);
}
ANS = 0;
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
if(ask(i,j,i,j)) continue;
ANS += dp[i][j];
ADD(ANS);
}
}
printf("%lld\n", ANS);
return 0;
}
I div1&2 (并查集)
//I石头剪刀布
//不能路径压缩,必须按秩合并
#include<bits/stdc++.h>
#define clr(a, b) memset(a,b,sizeof((a)))
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;
const int MXN = 1e6 + 7;
const LL MOD = 998244353;
int n, m, Q;
int fa[MXN], rk[MXN];
LL all[MXN], ke[MXN];//场数,客场数
LL ALL, KE;
LL ksm(LL a, LL b) {
LL res = 1;
while(b) {
if(b&1) res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
int Fi(int x) {
ALL = all[x]; KE = ke[x];
if(x == fa[x]) return x;
int tmp = fa[x];
while(tmp != fa[tmp]) {
ALL += all[tmp]; KE += ke[tmp];
tmp = fa[tmp];
}
ALL += all[tmp]; KE += ke[tmp];
return tmp;
}
int Find(int x) {
int ans = x;
if(x != fa[x]) {
int t = fa[x];
ans = Find(fa[x]);
ALL += all[t];
KE += ke[t];
}
return ans;
}
void UNION(int x,int y) {
int pa = Find(x), pb = Find(y);
if(pa == pb) return ;
++ all[pa]; ++ all[pb];
++ ke[pb];
if(rk[pa] < rk[pb]) swap(pa, pb);
++ rk[pa];
all[pb] -= all[pa];
ke[pb] -= ke[pa];
fa[pb] = pa;
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) fa[i] = i;
while(m --) {
int opt, x, y;
scanf("%d%d", &opt, &x);
if(opt == 1) {
scanf("%d", &y);
UNION(x, y);
}else {
ALL = all[x]; KE = ke[x];
Fi(x);//Find(x);
LL a = ALL - KE, b = KE, c = n - a - b;
printf("%lld\n", ksm(3, c) * ksm(2, a) % MOD);
}
}
return 0;
}
E div1&2 精简改良 生成树dp
迷之复杂度
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define eb emplace_back
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
inline LL read(){
LL x=0;int f=0;char ch=getchar();
while (ch<''0''||ch>''9'') f|=(ch==''-''),ch=getchar();
while (ch>=''0''&&ch<=''9'') x=(x<<3)+(x<<1)+ch-''0'',ch=getchar();
return x=f?-x:x;
}
inline void write(LL x) {
if(x==0){putchar(''0''),putchar(''\n'');return;}
if(x < 0) {putchar(''-'');x=-x;}
static char s[23];int l = 0;
while(x!=0)s[l++]=x%10+48,x/=10;
while(l)putchar(s[--l]);
putchar(''\n'');
}
const int INF = 0x3f3f3f3f;
const LL mod = 998244353;
const int MXN = 1e3 + 7;
int n, m;
std::vector<int> vs[(1<<14)+5];
LL dp[(1<<14)+5][20];
LL dis[20][20], N[(1<<14)+5];
int sta;
//for (int x = S; x; x = (x-1)&S))枚举子集,复杂度2^m,会漏掉空集
int main(int argc, char const *argv[]) {
#ifndef ONLINE_JUDGE
freopen("E://ADpan//in.in", "r", stdin);
//freopen("E://ADpan//out.out", "w", stdout);
#endif
n = read(), m = read();
//scanf("%d%d", &n, &m);
memset(dis, -1, sizeof(dis));
memset(dp, -1, sizeof(dp));
for(int i = 0, a, b, c; i < m; ++i) {
a = read(), b = read(), c = read();
//scanf("%d%d%d", &a, &b, &c);
dis[a][b] = dis[b][a] = c;
}
sta = 1 << n;
for(int i = 1; i < sta; ++i) {
for(int j = 0; j < n; ++j) if((i>>j)&1) vs[i].eb(j+1);
N[i] = vs[i].size();
}
LL tmp, ans = 0;
for(int i = 1, j = 1; i < sta; i <<= 1, ++j) dp[i][j] = 0;
for(int t = 1; t < sta; ++t) {
for(int old = (t-1)&t; old; old = (old-1)&t) {
for(auto i: vs[t]) {
if(dp[t-old][i]==-1) continue;
for(auto j: vs[old]) {
if(dis[i][j]==-1||dp[old][j]==-1) continue;
tmp = dp[old][j]+dp[t-old][i]+dis[i][j]*N[old]*(n-N[old]);
dp[t][i] = (dp[t][i]>tmp?dp[t][i]:tmp);
}
}
}
}
for(int i = 1; i <= n; ++i) ans = (ans>dp[sta-1][i]?ans:dp[sta-1][i]);
write(ans);
//printf("%lld\n", ans);
return 0;
}
day4
I div2 咆咆咆哮 (贪心)
//I
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
typedef pair<int, LL> piL;
}
using namespace lh;
const int MXN = 1e6 + 5;
const double eps = 1e-8;
int n;
LL dp[1005][1005];
struct lp {
LL a, b;
}cw[1005], tmp[1005];
bool cmp(const lp &A, const lp &B) {
if(A.a != B.a) return A.a > B.a;
return A.b < B.b;
}
bool cmp1(const lp &A, const lp &B) {
return (A.b-A.a) > (B.b-B.a);
}
int main(){
scanf("%d", &n);
LL ans = 0;
for(int i = 1; i <= n; ++i) {
scanf("%lld%lld", &cw[i].a, &cw[i].b);
ans += cw[i].a;
}
for(int t = 1; t < n; ++t) {
for(int i = 1; i <= n; ++i) {
tmp[i].a = cw[i].a;
tmp[i].b = cw[i].b * (n-t);
}
sort(tmp + 1, tmp + 1 + n, cmp1);
LL ret = 0;
for(int i = 1; i <= n; ++i) {
if(i <= t) ret += tmp[i].b;
else ret += tmp[i].a;
}
ans = max(ans, ret);
}
printf("%lld\n", ans);
return 0;
}
I div1 咆咆咆哮 (奇怪的三分+贪心)
//蜜汁三分
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define eb emplace_back
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
inline LL read(){
LL x=0;int f=0;char ch=getchar();
while (ch<''0''||ch>''9'') f|=(ch==''-''),ch=getchar();
while (ch>=''0''&&ch<=''9'') x=(x<<3)+(x<<1)+ch-''0'',ch=getchar();
return x=f?-x:x;
}
inline void write(LL x) {
if(x==0){putchar(''0''),putchar(''\n'');return;}
if(x < 0) {putchar(''-'');x=-x;}
static char s[23];int l = 0;
while(x!=0)s[l++]=x%10+48,x/=10;
while(l)putchar(s[--l]);
putchar(''\n'');
}
const int INF = 0x3f3f3f3f;
const LL mod = 998244353;
const int MXN = 1e5 + 7;
int n;
LL dp[1005][1005];
struct lp {
LL a, b;
}cw[1005], tmp[1005];
bool cmp(const lp &A, const lp &B) {
if(A.a != B.a) return A.a > B.a;
return A.b < B.b;
}
bool cmp1(const lp &A, const lp &B) {
return (A.b-A.a) < (B.b-B.a);
}
LL check(int t) {//t个b
LL ans = 0;
priority_queue<LL> Q;
for(int i = 1; i <= n; ++i) {
ans += cw[i].a;
Q.push(cw[i].b*(n-t)-cw[i].a);
}
while(t --) {
ans += Q.top(); Q.pop();
}
return ans;
}
int main(){
n = read();
LL ans = 0;
for(int i = 1; i <= n; ++i) {
cw[i].a = read(), cw[i].b = read();
ans += cw[i].a;
}
int L = 0, R = n, mid1, mid2;
LL res1, res2;
while(L <= R) {
mid1 = (2*L+R)/3;mid2 = (L+2*R)/3;
//mid1 = (L+R)/2;mid2 = (mid1+R)/2;
res1 = check(mid1);
res2 = check(mid2);
if(res1 > res2) R = mid2-1, ans = max(ans, res1);
else L = mid1+1, ans = max(ans, res2);
}
write(ans);
return 0;
}
C div2 (规律)
//C
相邻点度数均大于1就不行或者链长为3
K div2 两条路径(树形dp)
//K
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
namespace lh {
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
typedef pair<int, LL> piL;
}
using namespace lh;
const int MXN = 1e6 + 5;
const double eps = 1e-8;
int n, x;
std::vector<int> mp[MXN];
LL ar[MXN], mi[40], dp[MXN];
void dfs(int u,int ba) {
dp[u] = ar[u];
for(auto v: mp[u]) {
if(v == ba) continue;
dfs(v, u);
dp[u] = max(dp[u], dp[v] + ar[u]);
}
}
bool cmp(LL a, LL b) {
return a > b;
}
int main(){
mi[0] = 1;
for(int i = 1; i <= 32; ++i) mi[i] = mi[i-1] * 2;
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%lld", &ar[i]);
if(ar[i] >= 0) ar[i] = mi[ar[i]-1];
else ar[i] = -mi[-ar[i]-1];
//printf("%lld\n", ar[i]);
}
for(int i = 1, a, b; i < n; ++i) {
scanf("%d%d", &a, &b);
mp[a].push_back(b);
mp[b].push_back(a);
}
int Q; scanf("%d", &Q);
while(Q --) {
scanf("%d", &x);
for(int i = 1; i <= n; ++i) dp[i] = 0;
dfs(x, x);
std::vector<LL> vs;
for(auto v: mp[x]) {
if(dp[v] >= 0) vs.push_back(dp[v]);
}
sort(vs.begin(), vs.end(), cmp);
LL ans = ar[x];
for(int i = 0; i < vs.size() && i < 4; ++i) ans += vs[i];
//printf("**%lld\n", ans);
if(ans < 0) printf("-"), ans = -ans;
std::vector<int> v;
while(ans) {
if(ans & 1) v.push_back(1);
else v.push_back(0);
ans /= 2;
}
reverse(v.begin(), v.end());
for(auto s: v) {
printf("%d", s);
}
printf("\n");
}
return 0;
}
D div1&2 欧拉回路 (性质)
//D欧拉回路
//保证度数为偶数即可,注意特判2的情况
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define eb emplace_back
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
inline LL read(){
LL x=0;int f=0;char ch=getchar();
while (ch<''0''||ch>''9'') f|=(ch==''-''),ch=getchar();
while (ch>=''0''&&ch<=''9'') x=(x<<3)+(x<<1)+ch-''0'',ch=getchar();
return x=f?-x:x;
}
inline void write(LL x) {
if(x==0){putchar(''0''),putchar(''\n'');return;}
if(x < 0) {putchar(''-'');x=-x;}
static char s[23];int l = 0;
while(x!=0)s[l++]=x%10+48,x/=10;
while(l)putchar(s[--l]);
putchar(''\n'');
}
const int INF = 0x3f3f3f3f;
const LL mod = 998244353;
const int MXN = 1e3 + 7;
int n, m;
int main(int argc, char const *argv[]) {
scanf("%d%d", &n, &m);
if(m % 2 == 0 && n % 2 == 1) swap(n, m);
if(m == 2) swap(n, m);
LL ans = (n-1)*m + n*(m-1);
if(n == 2) {
ans = ans + ((m-2)/2)*2+(m%2==1);
}else if(n % 2 == 1) {
ans = (ans+((m-2)/2)*2+4+((n-2)/2)*2);
}else if(m % 2 == 1) {
ans = (ans+((m-2)/2)*2+4+(n-2)/2+(n-4)/2);
}else {
ans = (ans+m+n-4);
}
printf("%lld\n", ans);
return 0;
}
G div1&2 置置置换
$dp[i] = \sum_{j=1,j+=2}^{j<=i}dp[j-1]*dp[i-j]*COMB(i-1, j-1)$
/*
题意:有多少个n的排列满足:偶数位置小于奇数位置,奇数位置大于偶数位置;减增减增。。。的序列
*/
//上凸和下凸的答案是一样的
//dp[i]表示1-i的排列的合法情况总数
//枚举最大的数字i所在的位置:dp[i] = \sum_{j=1,j+=2}^{j<=i}dp[j-1]*dp[i-j]*COMB(i-1, j-1)
#include<bits/stdc++.h>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
#define eb emplace_back
#define o2(x) (x)*(x)
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
inline LL read(){
LL x=0;int f=0;char ch=getchar();
while (ch<''0''||ch>''9'') f|=(ch==''-''),ch=getchar();
while (ch>=''0''&&ch<=''9'') x=(x<<3)+(x<<1)+ch-''0'',ch=getchar();
return x=f?-x:x;
}
inline void write(LL x) {
if(x==0){putchar(''0''),putchar(''\n'');return;}
if(x < 0) {putchar(''-'');x=-x;}
static char s[23];int l = 0;
while(x!=0)s[l++]=x%10+48,x/=10;
while(l)putchar(s[--l]);
putchar(''\n'');
}
const int INF = 0x3f3f3f3f;
const LL mod = 1e9 + 7;
const int MXN = 1e4 + 7;
LL F[MXN], Inv[MXN], invF[MXN];
LL ksm(LL a, int b) {
LL res = 1;
for(;b;b>>=1,a=a*a%mod) {
if(b&1) res=res*a%mod;
}
return res;
}
int n;
LL dp[MXN];
void init() {
Inv[1] = F[1] = invF[1] = 1;
Inv[0] = F[0] = invF[0] = 1;
for(int i = 2; i < MXN; ++i) {
F[i] = F[i-1] * i % mod;
Inv[i] = (mod-mod/i)*Inv[mod%i] % mod;
invF[i] = invF[i-1] * Inv[i] % mod;
}
}
LL COMB(int n, int m) {
if(n == m || m == 0) return 1;
if(n < m) return 0;
return F[n]*invF[m]%mod*invF[n-m]%mod;
}
int main(){
n = read();
init();
dp[0] = dp[1] = dp[2] = 1;
for(int i = 3; i <= n; ++i) {
for(int j = 1; j <= i; j += 2) {
dp[i] = (dp[i] + dp[j-1] * dp[i-j]%mod * COMB(i-1, j-1)%mod)%mod;
}
}
printf("%lld\n", dp[n]);
return 0;
}
/*
d4G:
f[i][j]表示前i个位置,在剩下的第j小的方案数,枚举所有大于它的k。用前缀和或后缀和维护
1I/4G/7J
*/

2020 CCPC Wannafly Winter Camp Day1 - I. K 小数查询 (分块)
题目链接:K 小数查询
题意:给你一个长度为 $n$ 序列 $A$,有 $m$ 个操作,操作分为两种:
- 输入 $x,y,c$,表示对 $i\in [x,y] $,令 $A_{i}=min (A_{i},c)$
- 输入 $x,y,k$,表示询问区间 $[x,y]$ 中的第 $k$ 小数
思路:数据范围不是很大,可以分块来做,记录每个块已经更新过的最小值 $imin []$,询问时二分答案,然后求出 $[x,y]$ 区间中小于等于 $mid$ 的数的个数 $cnt$,通过判断 $cnt$ 与 $k$ 的大小来改变 $l,r$ 即可
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <cmath>
using namespace std;
const int N = 100010;
const int INF = 0x3f3f3f3f;
int block, belong[N], num, l[N], r[N], imin[N];
int n, m, a[N];
vector<int> v[N];
void build()
{
block = sqrt(n);
num = n / block;
if (n % block) num++;
for (int i = 1; i <= num; i++)
l[i] = (i - 1) * block + 1, r[i] = i * block;
r[num] = n;
for (int i = 1; i <= n; i++)
belong[i] = (i - 1) / block + 1;
for (int i = 1; i <= num; i++) {
imin[i] = INF;
for (int j = l[i]; j <= r[i]; j++)
v[i].push_back(a[j]);
sort(v[i].begin(), v[i].end());
}
}
void reset(int x)
{
v[x].clear();
for (int i = l[x]; i <= r[x]; i++) {
a[i] = min(a[i], imin[x]);
v[x].push_back(a[i]);
}
sort(v[x].begin(), v[x].end());
}
void update(int x, int y, int c)
{
int bl = belong[x], br = belong[y];
if (bl == br) {
for (int i = x; i <= y; i++)
a[i] = min(a[i], c);
reset(bl);
return;
}
for (int i = x; i <= r[bl]; i++)
a[i] = min(a[i], c);
reset(bl);
for (int i = l[br]; i <= y; i++)
a[i] = min(a[i], c);
reset(br);
for (int i = bl + 1; i < br; i++)
imin[i] = min(imin[i], c);
}
int query(int x, int y, int c)
{
int bl = belong[x], br = belong[y], cnt = 0;
if (bl == br) {
for (int i = x; i <= y; i++)
if (a[i] <= c || imin[bl] <= c) cnt++;
return cnt;
}
for (int i = x; i <= r[bl]; i++)
if (a[i] <= c || imin[bl] <= c) cnt++;
for (int i = l[br]; i <= y; i++)
if (a[i] <= c || imin[br] <= c) cnt++;
for (int i = bl + 1; i < br; i++)
if (imin[i] <= c) cnt = cnt + r[i] - l[i] + 1;
else cnt = cnt + upper_bound(v[i].begin(), v[i].end(), c) - v[i].begin();
return cnt;
}
int ask(int x, int y, int k)
{
int l = -1000000000, r = 1000000000;
while (l < r) {
int mid = (l + r) / 2;
if (query(x, y, mid) >= k) r = mid;
else l = mid + 1;
}
return l;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
build();
for (int i = 1; i <= m; i++) {
int kd, x, y, c;
scanf("%d%d%d%d", &kd, &x, &y, &c);
if (1 == kd) update(x, y, c);
else printf("%d\n", ask(x, y, c));
}
return 0;
}
2020 CCPC Wannafly Winter Camp Day1 Div.1&2总结
| 期望逆序对 | |
| 密码学 | 模拟 |
| 染色图 | |
| 生成树 | |
| 树与路径 | |
| 乘法 | 二分 |
| 圆凸包 | |
| 最大公约数 | 唯一分解定理 |
| k小数查询 | 区间线段树套权值线段树 |
| 德州扑克 |
B密码学
注意题目是给出所有操作后的结果,所以需要逆着操作即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
#include <map>
#include <set>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;
const int maxn = 1e3+5;
const int inf = 0x3f3f3f3f;
char s[1005][105];
char t[1005][105];
int n,m;
int xx[1005],yy[1005];
char change(char a,char b){//a是破解后的
int aa = 0,bb = 0,cc = 0;
if(a >= ''a'' && a <= ''z'')aa = a - ''a'';
else aa = a - ''A'' + 26;
if(b >= ''a'' && b <= ''z'')bb = b - ''a'';
else bb = b - ''A'' + 26;
if(aa >= bb){
cc = aa - bb;
}else{
cc = aa + 52 - bb;
}
aa = aa % 52;
if(cc >= 0 && cc <= 25)return cc + ''a'';
else return cc - 26 + ''A'';
}
void solve(){
for(int i = m; i >= 1; i--){
char x[105],y[105];
strcpy(x,t[xx[i]]);
strcpy(y,t[yy[i]]);
int l1 = strlen(x);
int l2 = strlen(y);
for(int j = 0; j < l2; j++){
y[j] = change(y[j],x[j%l1]);
}
strcpy(t[yy[i]],y);
}
}
void print(){
for(int i = 1; i <= n; i++){
cout << t[i] << endl;
}
}
int main(){
cin >> n >> m;
for(int i = 1; i <= m; i++){
scanf("%d%d",&xx[i],&yy[i]);
}
for(int i = 1; i <= n; i++){
cin >> s[i];
strcpy(t[i],s[i]);
}
solve();
print();
return 0;
}
F乘法
二分第k小的数字,mid 是一个数字,然后在数组b中进行遍历,看看这个数字在所有数字的排名情况 求出mid在一个常数*a[j]的所有情况的排名很简单,对于常数是0的情况,常数>0的情况,常数<0的情况,二分即可。 很妙的想法
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;
const int maxn = 1e5 + 5;
ll a[maxn],b[maxn];
ll n,m,k;
bool check(ll mid){
ll cnt = 0;
for(int i = 1; i <= m; i++){
if(b[i] == 0)cnt += mid<0?n:0;
if(b[i] < 0)cnt += lower_bound(a + 1, a + n + 1, ceil((double)mid / b[i])) - (a + 1);
if(b[i] > 0)cnt += n - ((upper_bound(a + 1, a + n + 1, floor((double)mid / b[i]))) - (a + 1));
// cout << cnt << endl;
}
return cnt <= k;
}
int main(){
cin >> n >> m >> k;
k--;
for(int i = 1; i <= n; i++){
scanf("%lld",&a[i]);
}
for(int i = 1; i <= m; i++){
scanf("%lld",&b[i]);
}
sort(a + 1,a + n + 1);
sort(b + 1,b + m + 1);
ll l = -1e13,r = 1e13;
while(l + 1 < r){
ll mid = (l + r) >> 1;
// cout << l << " " << mid << " " << r << endl;
if(check(mid))r = mid;
else l = mid;
}
cout << r << endl;
return 0;
}
H最小公约数
只需要对于gcd(i,y)对于i是[1,n]中除了k以外都不满足gcd(i,y) = gcd(k,y) 也就是gcd(y,k)的值是唯一的 而y只能是y的倍数才行,否则,对于k是质数的情况,gcd(k,y)会是1 那么只需要令ans = k,遍历[1,n]中k的倍数即可,如果说i是质数,那么乘上ans,因为根据唯一分解定理,所有数可以由质数乘积表示,要求出最小y,那么只需要质数即可,而ans初始值为k,因为y必须是k的倍数
import math
def is_prime(n):
if n == 1:
return False
for i in range(2, int(math.sqrt(n)) + 1):
if n % i == 0:
return False;
return True
t = int(input())
for tt in range(1, t + 1):
n, k = map(int, input().split())
ans = k
i = 2
while i * k <= n:
if is_prime(i):
ans *= i
i = i + 1
print(ans)
K小数查询
n,m的范围是$8*10^{4}$ 一种方法是可以暴力O(nm) 一种方法是主席树
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int maxn = 1e5 + 5;
int n,m;
int a[maxn];
int t[maxn];
int main(){
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i++)scanf("%d",&a[i]);
while(m--){
int c,l,r,k;
scanf("%d%d%d%d",&c,&l,&r,&k);
if(c == 1){
for(int i = l; i <= r; i++){
a[i] = min(a[i],k);
}
}else{
int sum = 0,last = 0;
memset(t,0,sizeof(t));
for(int i = l; i <= r; i++){
t[a[i]]++;
}
for(int i = 1; i <= n; i++){
last = sum;
sum += t[i];
if(last < sum && sum >= k){
printf("%d\n",i);
break;
}
}
}
}
return 0;
}
关于Day10 Intent部分隐士跳转的介绍已经告一段落,感谢您的耐心阅读,如果想了解更多关于16.oauth2 + oidc 实现 client部分、2019 wannafly winter camp day1-4代码库、2020 CCPC Wannafly Winter Camp Day1 - I. K 小数查询 (分块)、2020 CCPC Wannafly Winter Camp Day1 Div.1&2总结的相关信息,请在本站寻找。
本文标签:





