在本文中,我们将为您详细介绍LeetCode-ValidateBinarySearchTree的相关知识,此外,我们还会提供一些关于98.ValidateBinarySearchTree、Binary
在本文中,我们将为您详细介绍LeetCode - Validate Binary Search Tree的相关知识,此外,我们还会提供一些关于98. Validate Binary Search Tree、Binary Search Tree 以及一道 LeetCode 题目、leetcode 98 - Validate Binary Search Tree、LeetCode 98. Validate Binary Search Tree的有用信息。
本文目录一览:- LeetCode - Validate Binary Search Tree
- 98. Validate Binary Search Tree
- Binary Search Tree 以及一道 LeetCode 题目
- leetcode 98 - Validate Binary Search Tree
- LeetCode 98. Validate Binary Search Tree

LeetCode - Validate Binary Search Tree
Given a binary tree,determine if it is a valid binary search tree (BST). Assume a BST is defined as follows: The left subtree of a node contains only nodes with keys less than the node‘s key. The right subtree of a node contains only nodes with keys greater than the node‘s key. Both the left and right subtrees must also be binary search trees. Example 1: Input: 2 / 1 3 Output: true Example 2: 5 / 1 4 / 3 6 Output: false Explanation: The input is: [5,1,4,null,3,6]. The root node‘s value is 5 but its right child‘s value is 4.
如果对BST 中序遍历, 会产生有序数列。
/** * DeFinition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { //BST inorder traverse will generate a ordered sequnence public boolean isValidBST(TreeNode root) { if(root == null){ return true; } List<Integer> list = new ArrayList<>(); list.add(null); return helper(root,list); } public boolean helper(TreeNode node,List<Integer> list){ if(node == null){ return true; } boolean left = helper(node.left,list); if(list.get(list.size()-1) != null && node.val <= list.get(list.size()-1)){ return false; } list.add(node.val); boolean right = helper(node.right,list); return left && right; } }

98. Validate Binary Search Tree
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node''s key.
The right subtree of a node contains only nodes with keys greater than the node''s key.
Both the left and right subtrees must also be binary search trees.
Example 1:
Input:
2
/ \
1 3
Output: trueExample 2:
5
/ \
1 4
/ \
3 6
Output: false
Explanation: The input is: [5,1,4,null,null,3,6]. The root node''s value is 5 but its right child''s value is 4.
难度:medium
题目:给定二叉树,判断其是否为二叉搜索树。
思路:递归,并记录当前结点的取值范围。
Runtime: 0 ms, faster than 100.00% of Java online submissions for Validate Binary Search Tree.
Memory Usage: 37.6 MB, less than 100.00% of Java online submissions for Validate Binary Search Tree.
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public boolean isValidBST(TreeNode root) {
if (null == root) {
return true;
}
return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean isValidBST(TreeNode root, long minVal, long maxVal) {
if (null == root) {
return true;
}
if (root.val >= maxVal || root.val <= minVal) {
return false;
}
return isValidBST(root.left, minVal, root.val) && isValidBST(root.right, root.val, maxVal);
}
}
Binary Search Tree 以及一道 LeetCode 题目
一道LeetCode题目
今天刷一道LeetCode的题目,要求是这样的:
Given a binary search tree and the lowest and highest boundaries as
LandR, trim the tree so that all its elements lies in [L,R] (R >= L). You might need to change the root of the tree, so the result should return the new root of the trimmed binary search tree.
由于对于 Binary search tree 不理解,所以绕了点弯路,要解这道题,必须理解什么是 binary search tree。我们来看一下定义:
A binary search tree is a rooted binary tree, whose internal nodes each store a key (and optionally, an associated value) and each have two distinguished sub-trees, commonly denoted left and right. The tree additionally satisfies the binary search property, which states that the key in each node must be greater than or equal to any key stored in the left sub-tree, and less than or equal to any key stored in the right sub-tree.[1]:287 (The leaves (final nodes) of the tree contain no key and have no structure to distinguish them from one another.
看一下下面这个图一下子就能理解,就是说每个节点左边的值一定小于右边。
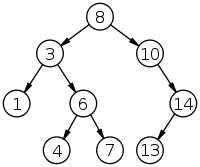
了解到这个约束,这个题目解起来就比较简单了:
class Solution:
def trimBST(self, root, L, R):
"""
:type root: TreeNode
:type L: int
:type R: int
:rtype: TreeNode
"""
if(root.val < L):
if(root.right != None):
root = self.trimBST(root.right, L, R)
else:
return None
elif(root.val > R):
if(root.left != None):
root = self.trimBST(root.left, L, R)
else:
return None
else:
if(root.left != None):
root.left = self.trimBST(root.left, L, R)
else:
root.left = None
if(root.right != None):
root.right = self.trimBST(root.right, L, R)
else:
root.right = None
return root
BST数据结构的一些算法特性
| Algorithm | Average | Worst case |
|---|---|---|
| Space | O(n) | O(n) |
| Search | O(log n) | O(n) |
| Insert | O(log n) | O(n) |
| Delete | O(log n) | O(n) |
参考资料: 1、Leetcode 2、Wiki Binary search tree
leetcode 98 - Validate Binary Search Tree
Given a binary tree,determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node‘s key.
The right subtree of a node contains only nodes with keys greater than the node‘s key.
Both the left and right subtrees must also be binary search trees.
时间空间均超70%的方法,写的有点复杂:
思路是,当前节点左右都满足BST的条件下,还要顺便找出左子树的最大值leftMax和右子树的最小值rightMin,以防leftMax大于root->val或rightMin 小于 root->val
class Solution { public: bool isValidBST(TreeNode *root) { int subLeftMax = INT_MIN,subLeftMin = INT_MAX,subRightMax = INT_MIN,subRightMin = INT_MAX; return this->dovalid(root,&subLeftMax,&subLeftMin,&subRightMax,&subRightMin); } protected: bool dovalid(TreeNode *root,int *leftMaxVal,int *leftMinVal,int *rightMaxVal,int *rightMinVal) { bool result = true; int subLeftMax = INT_MIN,subRightMin = INT_MAX; if (root == NULL || (root->left == NULL && root->right == NULL)) { return true; } if ((root->left != NULL && root->left->val >= root->val) || (root->right != NULL && root->right->val <= root->val)) { return false; } result = this->dovalid(root->left,&subRightMin); if (result == false || (root->left != NULL && subLeftMax >= root->val) || (root->left != NULL && subRightMax >= root->val)) { return false; } *leftMaxVal = max(max(subLeftMax,subRightMax),(root->left == NULL ? INT_MIN : root->left->val)); *leftMinVal = min(min(subLeftMin,subRightMin),(root->left == NULL ? INT_MAX : root->left->val)); subLeftMax = subRightMax = INT_MIN; subLeftMin = subRightMin = INT_MAX; result = this->dovalid(root->right,&subRightMin); if (result == false || (root->right != NULL && subLeftMin <= root->val) || (root->right != NULL &&subRightMin <= root->val)) { return false; } *rightMaxVal = max(max(subLeftMax,(root->right == NULL ? INT_MIN : root->right->val)); *rightMinVal = min(min(subLeftMin,(root->right == NULL ? INT_MAX : root->right->val)); return true; } };

LeetCode 98. Validate Binary Search Tree
最容易想到的思路就是中序遍历,然后看是不是递增数列。
也可以像下面这样,用最大最小值区间来判断
class Solution { public: bool helper(TreeNode* node,long mn,long mx){ if(!node) return true; if(node->val<=mn || node->val>=mx) return false; return helper(node->left,mn,node->val) && helper(node->right,node->val,mx); } bool isValidBST(TreeNode* root) { return helper(root,LONG_MIN,LONG_MAX); } };
今天关于LeetCode - Validate Binary Search Tree的介绍到此结束,谢谢您的阅读,有关98. Validate Binary Search Tree、Binary Search Tree 以及一道 LeetCode 题目、leetcode 98 - Validate Binary Search Tree、LeetCode 98. Validate Binary Search Tree等更多相关知识的信息可以在本站进行查询。
本文标签:





