GVKun编程网logo

推销员问题（推销员问题可以通过弗洛伊德算法求解）

22

对于想了解推销员问题的读者，本文将提供新的信息，我们将详细介绍推销员问题可以通过弗洛伊德算法求解，并且为您提供关于5年程序员问我：什么是断言？、Android程序员问答题、C++模板类里的静态成员问题

对于想了解推销员问题的读者，本文将提供新的信息，我们将详细介绍推销员问题可以通过弗洛伊德算法求解，并且为您提供关于5年程序员问我：什么是断言？、Android 程序员问答题、C++ 模板类里的静态成员问题、C语言使用回溯法解旅行售货员问题与图的m着色问题的有价值信息。

本文目录一览：

推销员问题（推销员问题可以通过弗洛伊德算法求解）

推销员问题（推销员问题可以通过弗洛伊德算法求解）

　　旅行商问题，即TSP问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

　　这是我大二期末数据结构课程设计的题目之一，其是关于图这种数据结构的。按照其题目大意可以大致理解为一个旅行商，要从自己原本的城市出发，走遍所有的城市最后回到自己原来的城市。在这个问题中的约束是每个城市都只能拜访一次。目的是求旅行商走一圈得到的最短路径的大小。

　　对于这个问题，普遍有两种思路。第一种思路是暴力破解法。

　　举个例子。

　　

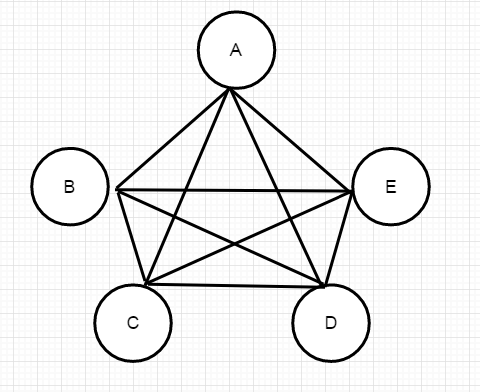
　　如图所示，一共有五个城市其彼此之间相互连通。旅行商要走完一圈回来且不重复，实际上走得路径的各种可能性也不过是各种城市的排列组合。

ABCDEA、ACBDEA、......等等，按照排列组合来计算共有4!种情况，在这些组合中选取一种距离最短的方式就好了。当城市数为5的时候看起来还好，但是这种暴力排列组合的时间复杂度是很大的，达到了O(n!)，所以对于城市数多的情况下，是很难算出结果的。

　　第二种，就是贪心法。所谓贪心法，就是每一步都走最短的路径，且通往的城市是没有访问过的。这种方法，可以得到尽可能短的路径，但是也会出现一种问题，就是局部最优解不一定是整体最优解，你可能一味的贪心得到是这样的结果，之前走的路都是最短的，但是最后返回原来城市的路径究极长，显然就不满足最短路径了。我的方法就属于这种贪心法，废话不多说了，上代码。

# include <stdio.h>
# include <string.h>
# include <stdlib.h>
# include <iostream>
# define INF 100000
# define max 100
using namespace std;
//推销员问题
typedef struct Graph{
    int distance[max][max];//城市与城市之间的距离 
    char place[max];
    int city;//城市的个数 
    int edge;//边的个数 
}CI,*PCI;//城市 
bool visited[max];//判断有没有访问过该城市
int order[max];//访问节点的顺序 
int  num_vertax(void);//求已经收入顶点集合的顶点的个数 
void init_graph(CI* G);//初始化城市 
void find_bestway(CI*G);//找到最好的路径
int locate_graph(CI*G,char elem);//找到顶点的下标位置
void show_graph(CI* G);//把图打印出来 
int main(void)
{
    char elem;
    PCI G=(PCI)malloc(sizeof(CI));
    
    init_graph(G);
    show_graph(G);
    find_bestway(G);
    free(G); 
    system("pause");
    return 0;
 } 
 void init_graph(CI* G)
 {
     int i,j;
     printf("请输入一共有多少个城市：\n");
     scanf("%d",&(G->city));
     ///初始化城市 
     for(i=0;i<G->city;i++)
     {
         for(j=0;j<G->city;j++)
         {
             if(i==j)
             {
                 G->distance[i][j]=0;
             }
             else
             {
                 G->distance[i][j]=INF;
             }
         }
     }
     printf("请输入城市的名称：\n");
     for(i=0;i<G->city;i++)
     {
         cin>>G->place[i];
     }
     ///输入城市与城市之间的距离
     for(i=0;i<G->city;i++)
     {
         for(j=0;j<G->city;j++)
         {
             if(G->distance[j][i]!=0&&G->distance[j][i]!=INF)
             {
                 G->distance[i][j]=G->distance[j][i];
             }
            else if(i!=j) 
             {
                 
                 printf("请输入%c城市与%c城市之间的距离：\n",G->place[i],G->place[j]);
                 scanf("%d",&G->distance[i][j]);
             }
         }
      } 
      
 }
 void find_bestway(CI* G)
 {///找到最好的路径并输出出来 
     char begin;//开始的城市
     int start;//开始城市的下标
    int end;//结束城市的下标 
    int remain;//记录下标 
    int count=1;//计数器
    int cost=0;//花费
    int next;
    int min_cost=0;//总的最小花费 
    for(int i=0;i<G->city;i++)//初始化所有城市都没有访问过 
    {
        visited[i]=false;
    }
    for(int i=0;i<max;i++)//顺序序号数组我们用-1初始化 
    {
        order[i]=-1;
    }
     cout<<"请输入您想从哪个城市出发"<<endl;
    cin>>begin;
    start=locate_graph(G,begin);
    cout<<"start="<<start<<endl;
    //开始的那一座城市声明已经访问过了
    remain=start;
    cout<<"remain="<<remain<<endl;
    visited[start]=true;
    order[0]=start;//访问顺序的第一个位置装着该下标
    while(num_vertax()<G->city)
    {
    //    cout<<"有"<<num_vertax()<<"个顶点已经加入"<<endl; 
        cost=INF;//初始化最大长度
        for(int i=0;i<G->city;i++)//在与它相邻的所有节点中
        {
             if(start!=i&&visited[i]==false&&G->distance[start][i]<cost)
             {
             //    cout<<"start="<<start<<endl;
             //    cout<<"i="<<i<<endl;
             //    cout<<"distance="<<G->distance[start][i]<<endl;
                 cost=G->distance[start][i];
             //    cout<<"第"<<"i="<<i<<"时候"<<cost<<endl; 
                 next=i;
                 
             }            
        } 
        //cout<<"start="<<start<<" ";
        start=next;
         visited[start]=true;//下一个开始的节点为访问过了
         order[count]=start;
         cout<<"cost="<<cost<<endl;
         min_cost=min_cost+cost;
         count++; 
    }
    
    //cout<<"之前min_cost="<<min_cost<<endl;
    order[count]=order[0];
    //cout<<"最后一段路为："<<G->distance[count-1][remain]; 
    //cout<<"remain="<<remain<<endl;
    //cout<<"最后节点下标为"<<order[count]<<endl;
//    cout<<"count="<<count; 
    //cout<<"last="<<G->distance[count][remain];
    min_cost=min_cost+G->distance[order[count-1]][remain];
    cout<<"最佳访问顺序为："<<endl;
    for(int i=0;i<G->city+1;i++)
    {
        cout<<G->place[order[i]]<<" ";
    }
    cout<<endl;
    cout<<"最短的距离为:"<<endl;
    cout<<min_cost;
     cout<<endl;
       
    
    
      
     
 } 
int locate_graph(CI* G,char elem)//返回节点所在的下标 
{
    int i;
    for( i=0;i<G->city;i++)
    {
        if(elem==G->place[i])
        {
          return i;
        }
    }
    
    
} 
int  num_vertax(void)//可以知道顶点集合之中一共有多少个顶点 
{ 
    
    int count=0;
    while(order[count]!=-1)
    {
        count++;
    }
    return count;
}
void show_graph(CI* G)//将图的内容打印出来
{
    int i,j;
    printf("图的内容为：\n");
    for(i=0;i<G->city;i++)
    {
        printf("%c\t",G->place[i]);
     }
    printf("\n");
    for(i=0;i<G->city;i++)
    {
        for(j=0;j<G->city;j++)
        {
            printf("%d\t",G->distance[i][j]);
        }
        printf("\n");
     } 
}

 

5年程序员问我：什么是断言？

5年程序员问我：什么是断言？

响应以及断言

在“发送HTTP请求”一讲中，我们讲解了APIPOST中响应数据的查看。

API 请求响应

点击发送按钮后，如果有数据返回，则会显示返回数据，响应时间，响应码，Cookie等。

注意：返回数据默认是 ==美化== 模式，便于查看 JSON XML 格式。您可以通过切换 ==原生== 或 ==预览== 模式 查看其它类型的类型。

返回Headers

除了查看结果外，ApiPost也提供了强大的测试校验功能。在这里我们也可以使用断言来进行响应结果的校验。

响应结果分屏展示

在APIPOST 5.4版本后，支持“响应结果分屏展示”，从而提升工作区的空间。

image.png

image.png

什么是断言？

协作开发，版本升级，服务器升级，接口返回有可能因为一些bug，和我们预期结果不一致。为了便于开发&测试人员能够更快的发现bug，有利于整个产品质量以及进度的保证。我们推出断言功能。

如何使用断言？

  1. 定义测试用例
  2. 验证测试用例

例如接口返回：

{
    "errcode": 0,
    "errstr": "success",
    "post": [],
    "get": [],
    "request": [],
    "put": "",
    "header": {
        "Host": "echo.apipost.cn",
        "Connection": "keep-alive",
        "Content-Length": "0",
        "Accept": "application/json, text/javascript, */*; q=0.01",
        "Accept-Encoding": "gzip, deflate, br",
        "Accept-Language": "zh-CN",
        "Content-Type": "application/json",
        "Cookie": "PHPSESSID=n3k73k06o6ghnie4e9re4rbf0t",
        "Origin": "https://echo.apipost.cn",
        "User-Agent": "Mozilla/5.0 (iPhone; CPU iPhone OS 13_2_3 like Mac OS X) AppleWebKit/605.1.15 (KHTML, like Gecko) Version/13.0.3 Mobile/15E148 Safari/604.1"
    }
}

定义测试用例：

apt.assert(''response.raw.status==200'');
apt.assert(''response.raw.type=="json"'');
apt.assert(''response.json.errcode==0'');
apt.assert(''response.raw.responseTime<100'');
apt.assert(''response.json.header.Host=="echo.apipost.cn"'');

点击发送按钮后：

绿色表示测试通过，红色表示测试不通过。

特别注意：==每个测试用例是一行，不能换行。==

例：apt.assert(''response.json.header.Host=="echo.apipost.cn"'');

1）response.json.header.Host 表示响应json下面的header数组中的Host字段，
2）必须都为1，才会通过。

常见的测试用例可以通过后执行脚本获取：

更多响应参数变量

response.raw：原始响应数据

调用示例：

response.raw.status //响应状态码（200、301、404等）
response.raw.responseTime //响应时间（毫秒）
response.raw.type //响应类型（json等）
response.raw.responseText //响应文本

response.json：json格式的响应数据

调用示例如上面示例：

response.json.data.token //也可以 response.json.data["token"]

response.headers：响应头

调用示例：

response.headers.server //也可以 response.headers["server"]

response.cookies ：响应cookie

调用示例：

response.cookies.PHPSESSION //也可以 response.cookies["PHPSESSION"]

常用断言表达式

1、检查response body中是否包含某个string

apt.assert(''response.raw.responseText=="test"'');  // 检查响应文本是否等于test字符串 
apt.assert(''response.raw.responseText.indexOf("test") > -1'');  // 检查响应文本是否含有test字符串

2、检测返回JSON中的某个值是否等于预期的值

apt.assert(''response.json.hasOwnProperty("errcode")''); // 检测返回json对象的是否含有errcode字段
apt.assert(''response.json.errcode=="success"'');  // 检测返回json对象的errcode字段是否等于success字符串
apt.assert(''response.json.errcode.indexOf("success") > -1'');  // 检测返回json对象的errcode字段是否含有success字符串
apt.assert(''response.json.errcode!="success"'');  // 检测返回json对象的errcode字段是否不等于success字符串
apt.assert(''response.json.errcode>=1'');  // 检测返回json对象的errcode字段是否大于1
apt.assert(''response.json.errcode==null''); // 检测返回json对象的errcode字段是否是null

3、测试response Headers中的某个元素是否存在(如:Content-Type)

apt.assert(''response.headers.hasOwnProperty("content-type")'');

4、验证Status code（响应码）的值是不是等于200

apt.assert(''response.raw.status==200'');

5、验证Response time（请求耗时）是否大于某个值

apt.assert(''response.raw.responseTime>=100'');

6、验证返回类型是不是json

apt.assert(''response.raw.type=="json"'');

Android 程序员问答题

Android 程序员问答题

版权声明：本文为博主原创文章，未经博主允许不得转载， 微信公众号『醉翁猫咪』特约作者

输入图片说明

前言 最近三个月内，不断地进行移动应用开发在线测试题，也积累了不一样的知识。这也将对 android studio 有很好的掌握，对将来面试也很有好处。那么我就分享给大家。分享是一种幸福，这是一种质的飞越。

我的答题也可能存在出现错误的地方，欢迎指正，如果对于文章中的某些部分有不同的理解和想法，或者有更好的想法，欢迎留言讨论。

答题参考资料：

资料网址：http://www.android-doc.com/index.html，http://bbs.51cto.com/thread-954794-1.html，https://baike.so.com/doc/7013643-7236530.html，http://www.android-doc.com/reference/android/app/Activity.html，

材料答题 1. 什么是 Activity?

activity 是 Android 组件中最基本也是最为常见用的四大组件之一。Android 四大组件有 Activity 活动，Service 服务，Content Provider 内容提供，BroadcastReceiver 广播接收器。

Activity 简单说，四大组件之一，一个与用户交互界面对应的 activity。activity 是 Context 的子类，通过 setContentView (View) 来显示指定控件的。

onCreate (Bundle) 是你初始化活动的地方，而 onPause () 是你处理用户离开你的活动的地方。

Activity 类是应用程序整个生命周期的重要组成部分，活动的发起和组装是平台应用程序模型的基本组成部分。

我相信学习 Activity，必定需要理解生命周期图

public class Activity extends ApplicationContext{
     protected void onCreate(Bundle icicle);
     protected void onStart();
     protected void onRestart();

     protected void onResume();
     protected void onFreeze(Bundle outIcicle);

     protected void onPause();
     protected void onStop();
     protected void onDestroy();

这里描述了 onCreate (Bundle) 函数是你进行初始化的地方，这个也是执行 onContentView (View) 函数的地方，setContentView (View) 函数可以传入一个由 XML 编制的 UI 界面，可以使 UI 和具体实现完全分离。onPause () 函数是处理用户离开当前 Activity 的地方。更重要的是，任何在当前 Activity 中的任何改变都要在这个函数中提交。

生命周期：在整个的生命周期，从 onCreate (Bundle) 开始到 onDestroy () 结束。从 onStart () 开始到 onStop () 结束。从 onResume () 开始到 onPause (() 结束。

所以 Activity 生命周期：包含的回调方法有，onCreate (); onStart (); onResume (); onPause (); onStop (); onDestroy ()

2.Activity, Intent, Service 是什么关系？

Activity 是负责用户界面的显示和交互，Service 负责后台任务的处理，Activity 和 Service 之间是通过 Intent 传递数据，因此可以把 Intent 看作是通信使者。

在同一个 app 来说，Service 和 Activity 在同一个线程。

3.Service 服务

服务是一个应用程序组件，代表应用程序希望在不与用户交互的情况下执行长时间运行的操作，或者提供其他应用程序使用的功能。

4. 什么是服务？

服务不是一个单独的过程。服务对象并不意味着它在自己的进程中运行，除非另有说明，它运行在与它所属的应用程序相同的进程中。 服务不是一个线程。 在 Service 服务中的回调方法有 onCreate, onStart, onDestroy, onBind 和 onUnbind。

5. 广播接收器 BroadcastReceiver

BroadCastReceiver 是 Android 四大组件之一，主要用于接收系统或者 app 发送的广播事件。广播分两种：有序广播和无序广播。无序广播：完全异步，逻辑上可以被任何广播接收者接收到。有序广播：按照被接收者的优先顺序，在被接受者中传播。

注册广播接收者

静态：

<receiver android:name=".BroadcastReceiver1">
    <intent-filter>
        <action android:name="android.intent.action.CALL">
    </intent-filter>
</receiver>

动态：


receiver = new BroadcastReceiver();
IntentFilter intentFilter = new IntentFilter();
intentFilter.addAction(CALL_ACTION);
context.registerReceiver(receiver, intentFilter);

6.Android 的数据存储方式

File 存储，sharePrefernce 存储，ContentProvider 存储，SQLiteDataBase 存储，网络存储。

7.ContentProvider

内容提供者是 Android 应用程序的主要构建，为应用程序提供内容。它们封装数据并通过单一 ContentResolver 接口将其提供给应用程序使用。方法：onCreate ()，query ()，insert ()，update ()，delete ()，getType ()。

8.Activity 启动模式

standard 是活动默认的启动模式，在不进行显式指定的情况下，所有活动都会自动使用这种模式。标准启动一个新的 activity 压入栈中。 singleTop 是在启动活动时如果发现返回栈的栈顶已经是该活动，则认为可以直接使用它。 singleTask 是如果每次启动时系统首先会在返回栈中检查是否存在该活动的实例。 singleInstance 是两个应用都要调到 activity，如果发现另一个应用存在 activity 栈则共享不新建。 9.ListView


public class MyListView extends Activity{
  private ListView listView;
  @Override
  public void onCreate(Bundle savedInstanceState){
    super.onCreate(savedInstanceState);
    listView = new listView(this);
    listView.setAdapter(new ArrayAdapter<String>(this,R.layout.simple_listview,getData()));
    setContentView(listView);
private list<String> getData(){
    list<String> data = new ArrayList<String>();
    data.add("醉翁猫咪");
    return data;
    }
}

10.Intent 传递

Intent 是要执行的操作的抽象描述。Intent 为在不同应用程序中的代码之间执行延迟的运行时绑定提供了一种工具。其最重要的用途是开展活动，在活动中它可以被认为是活动之间的胶水。它基本上是一个被动的数据结构，对被执行的动作进行抽象描述。

11.Fragment 的生命周期

生命周期：onAttach ()–>onCreate ()–>onCreateView ()–>onActivityCreated ()–>onViewStateRestored ()–>onStart ()–>onResume ()。

12.Android 泄露的那些事？

内存泄漏简单地说，申请了一块内存空间，使用完毕后没有释放掉。

它的一般表现是：程序运行时间越长，占用内存越多，最终用尽全部内存，导致整个系统崩溃。

内存泄漏的的原因： 数据库没有关闭游标 cursor 构造 Adapter 时，没有使用 convertView Bitmap 对象不在使用时，调用 recycle () 释放内内存对象被生命周期长的对象引用。

13.mvc 模式

MVC 为 Model-View-Controller，分为三个层 — 模型层，视图层，控制层。View 视图是指用户看到并与之交互的界面，model 模型是指模型表示业务规则，controller 控制器是指控制器接受用户的输入并调用模型和视图去完成用户的需求，控制器本身不输出任何东西和做任何处理。

总结：

Android 程序员是指从事 Android 移动应用操作系统、游戏和各种 Android 平台功能的应用、开发和测试的技术人员。Android 工程师异常吃香，有一年开发经验的 Android 工程师的月薪在 8000 元左右。

关注我，每天都有优质技术文章推送，工作，学习累了的时候放松一下自己。 输入图片说明

C++ 模板类里的静态成员问题

C++ 模板类里的静态成员问题

    这两天没事找了本《STL 源码剖析》看下，可是刚看开头就出问题了，（本人菜鸟）特来请教

问题是这样的，书中有个测试 stl_config.h 中的各种组态问题，第一个例子 

#include <iostream>
using namespace std;

template <typename T>
class testClass
{
public:
	static int _data;
};

int testClass <int>::_data = 1;	//这里出错
int testClass <char>::_data = 2;

int main(int argc, char *argv[])
{
	cout << testClass< int >::_data << endl;
	cout << testClass< char >::_data << endl;
	return 0;
}

在初始化静态变量是出错了

11 5  [Error] specializing member ''testClass<int>::_data'' requires ''template<>'' syntax

不明白为何出错，必须写为下面这样吗？ 

template <typename T>
int testClass <T>::_data = 1;

如果是，那岂不是书中出错？（我是菜鸟，觉得这么有名的书，估计没错吧）特来请教！！





C语言使用回溯法解旅行售货员问题与图的m着色问题

C语言使用回溯法解旅行售货员问题与图的m着色问题

旅行售货员问题
1.问题描述：

旅行售货员问题又称TSP问题，问题如下：某售货员要到若干个城市推销商品，已知各城市之间的路程（或旅费），他要选定一条从驻地出发，经过每个城市一遍最后回到驻地的路线，使总的路线（或总的旅费）最小。数学模型为给定一个无向图，求遍历每一个顶点一次且仅一次的一条回路，最后回到起点的最小花费。

2.输入要求：

输入的第一行为测试样例的个数T（ T < 120 ），接下来有T个测试样例。每个测试样例的第一行是无向图的顶点数n、边数m（ n < 12，m < 100 ），接下来m行，每行三个整数u、v和w，表示顶点u和v之间有一条权值为w的边相连。（ 1 <= u < v <= n，w <= 1000 ）。假设起点（驻地）为1号顶点。

3.输出要求：

对应每个测试样例输出一行，格式为"Case #: W"，其中'#'表示第几个测试样例（从1开始计），W为TSP问题的最优解，如果找不到可行方案则输出-1。

4.样例输入：

2
5 8
1 2 5
1 4 7
1 5 9
2 3 10
2 4 3
2 5 6
3 4 8
4 5 4
3 1
1 2 10

5.样例输出：

Case 1: 36
Case 2: -1

6.解决方法：

//旅行售货员问题 （回溯）
#include<iostream> 
#define N 100 
using namespace std; 
int n,m,w,//图的顶点数和边数
  graph[N][N],//图的加权邻接矩阵
  c=0,//当前费用
  bestc=-1,//当前最优值
  x[N],//当前解
  bestx[N];    //当前最优解
void backtrack(int k); 
void swap(int &a,int &b); 
void swap(int &a,int &b) 
{ 
  int temp=a; 
  a=b; 
  b=temp; 
} 
void backtrack(int k) 
{ 
  if(k==n) 
  { 
    if( (c+graph[x[n-1]][x[n]]+graph[x[n]][1]<bestc||bestc==-1) && graph[x[n-1]][x[n]]!=-1 && graph[x[n]][1]!=-1 ) 
    { 
      bestc=c+graph[x[n-1]][x[n]]+graph[x[n]][1]; 
      for(int i=1;i<=n;i++) 
      { 
        bestx[i]=x[i]; 
      } 
    } 
    return ; 
  } 
  else 
  { 
    for(int i=k;i<=n;i++) 
    { 
      if( graph[x[k-1]][x[i]]!=-1 && (c+graph[x[k-1]][x[i]]<bestc || bestc==-1)) 
      { 
        swap(x[i],x[k]); 
        c+=graph[x[k-1]][x[k]]; 
        backtrack(k+1); 
        c-=graph[x[k-1]][x[k]]; 
        swap(x[i],x[k]); 
      } 
    } 
  } 
} 


int main(void)
{
  int i,j,tmp=1,testNum;
  cin>>testNum;
  while(tmp<=testNum)
  {
    cin>>n>>m;
    for(i=1;i<=n;i++)
    for(j=1;j<=n;j++)
    graph[i][j]=-1;
    for(int k=1;k<=m;k++)
    {
      cin>>i>>j>>w;
      graph[i][j]=w;
      graph[j][i]=w;
    }
    for(i=1;i<=n;i++)
    {
      x[i]=i;
      bestx[i]=i;
    }
    backtrack(2);
    cout<<"Case "<<tmp<<": "<<bestc<<endl;
    bestc=-1;
    c=0;
    
    tmp++;
  }  
  
  return 0;
}

图的m着色问题
1.问题描述
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色，求有多少种方法为图可m着色。

2.输入要求：
输入的第一个为测试样例的个数T （ T < 120 ），接下来有T个测试样例。每个测试样例的第一行是顶点数n、边数M和可用颜色数m（ n <= 10，M < 100，m <= 7 ），接下来M行，每行两个整数u和v，表示顶点u和v之间有一条边相连。（ 1 <= u < v <= n ）。

3.输出要求：
对应每个测试样例输出两行，第一行格式为"Case #: W"，其中'#'表示第几个测试样例（从1开始计），W为可m着色方案数。

4.样例输入：

1
5 8 5
1 2
1 3
1 4
2 3
2 4
2 5
3 4
4 5

5.样例输出：

Case 1: 360

6.解决方法：

#include<iostream>
using namespace std;
#define N 100
int m,n,M,a[N][N],x[N],textNum;
int static sum=0;

bool ok(int k)
{
  for(int j=1;j<=n;j++)
  if(a[k][j]&&(x[j]==x[k]))
  return false;
  return true;
}


void backtrack(int t)
{
  if(t>n)
  {
    sum++;
    // for(int i=1;i<=n;i++)
    //cout<<x[i]<<" ";
    //cout<<endl;
  }
  else
  for(int i=1;i<=m;i++)
  {
    x[t]=i;
    if(ok(t))
    backtrack(t+1);
    x[t]=0;
  }
}

int main()
{
  int i,z=1;
  cin>>textNum;         //输入测试个数
  while(textNum>0)
  {
    cin>>n;          //输入顶点个数
    for(i=1;i<=n;i++)
    for(j=1;j<=n;j++)
    a[i][j]=0;
    cin>>M>>m;         //输入边的个数、可用颜色数
    for(int k=1;k<=M;k++)   //生成图的邻接矩阵
    {
      cin>>i>>j;
      a[i][j]=1;
      a[j][i]=1;
    }
    /* for(i=1;i<=n;i++){
      for(j=1;j<=n;j++)
      cout<<a[i][j]<<" ";
    cout<<endl;}*/
    for(i=0;i<=n;i++)
    x[i]=0;
    backtrack(1);
    cout<<"Case "<<z<<": "<<sum<<endl;
    sum=0;
        
    textNum--;
    z++;
  }
    
  return 0;
}

关于推销员问题和推销员问题可以通过弗洛伊德算法求解的问题就给大家分享到这里，感谢你花时间阅读本站内容，更多关于5年程序员问我：什么是断言？、Android 程序员问答题、C++ 模板类里的静态成员问题、C语言使用回溯法解旅行售货员问题与图的m着色问题等相关知识的信息别忘了在本站进行查找喔。

本文标签：

上一篇dedecms织梦手机站去除新闻内容中图片的宽高达到自适应（如何删除织梦广告）

下一篇[普及]NOIP 2015 推销员 贪心（推销员之死百度百科）

相关文章