对于NOIP2015T4推销员感兴趣的读者,本文将会是一篇不错的选择,我们将详细介绍推销员doortodoor2002,并为您提供关于2018/7/16YMOI模拟NOIP2013D2T3华容道、63
对于NOIP2015 T4 推销员感兴趣的读者,本文将会是一篇不错的选择,我们将详细介绍推销员door to door2002,并为您提供关于2018/7/16 YMOI 模拟 NOIP2013D2T3 华容道、6359. 【NOIP2019 模拟 2019.9.15】小 ω 的树 (tree)(定期重构)、BZOJ 4326: NOIP2015 运输计划、BZOJ 4326: NOIP2015 运输计划 (二分,树上差分)的有用信息。
本文目录一览:- NOIP2015 T4 推销员(推销员door to door2002)
- 2018/7/16 YMOI 模拟 NOIP2013D2T3 华容道
- 6359. 【NOIP2019 模拟 2019.9.15】小 ω 的树 (tree)(定期重构)
- BZOJ 4326: NOIP2015 运输计划
- BZOJ 4326: NOIP2015 运输计划 (二分,树上差分)

NOIP2015 T4 推销员(推销员door to door2002)
题面
【问题描述】
阿明是一名推销员,他奉命到螺丝街推销他们公司的产品。螺丝街是一条死胡同,出口与入口是同一个,街道的一侧是围墙,另一侧是住房。螺丝街一构有N 家住房,第i 家住户到入口的距离为si 米。由于同一栋房子里可以有多家住户,所以可能有多家住房与入口的距离相等。阿明会从入口进入,依次向螺丝街的X 家住房推销产品,然后再原路走出去。阿明每走1 米就会积累1 点疲劳值,向第i 家住房推销产品会积累Ai 点疲劳值。阿明是工作狂,他想知道,对于不同的X,在不走多余路的前提下,他最多可以积累多少点疲劳值。
【输入格式】
第一行有一个正整数N,表示螺丝街住房的数量。
接下来的一行有N 个正整数,其中第i 个整数Si 表示第i 家住户到入口的距离。数据保证S1≤s2≤…≤Sn≤10^8。
接下来的一行有N 个整数,其中第i 个整数Ai 表示向第i 户住户推销产品会积累的疲劳值。数据保证Ai<10^3。
【输出格式】
输出N 行,每行一个正整数,第i 行整数表示当X=i 时,阿明最多积累的疲劳值。
思路
我见过NOIP T4最水的题,没有之一。
这道题算法为贪心(废话),但应该怎么贪呢?
首先,通过我们分析可得,最大值一定是取x个最大值+2*已取数的最大距离或x-1个最大值+2*所有数的最大距离+最远且最大的数。所以需要三个数组,sum(前x个数的总和),maxlen(前x个数最远距离),h(2*所有数的最大距离+最远且最大的数)
代码
1 #include
2 using namespace std;
3 int n,sum[100005],maxlen[100005],h[100005];
4 struct node{int s,a;}x[100005];
5 bool cmp(node p,node q)
6 {
7 return p.a>q.a;
8 }
9 int main()
10 {
11 cin>>n;
12 for (int i=1;i<=n;i++) cin>>x[i].s;
13 for (int i=1;i<=n;i++) cin>>x[i].a;
14 sort(x+1,x+n+1,cmp);
15 for (int i=1;i<=n;i++) sum[i]=sum[i-1]+x[i].a;
16 for (int i=1;i<=n;i++) maxlen[i]=max(maxlen[i-1],x[i].s);
17 for (int i=n;i>=1;i--) h[i]=max(h[i+1],x[i].s*2+x[i].a);
18 for (int i=1;i<=n;i++) cout<
19 return 0;
20 }

2018/7/16 YMOI 模拟 NOIP2013D2T3 华容道
题目描述 Description
小 B 最近迷上了华容道,可是他总是要花很长的时间才能完成一次。于是,他想到用编程来完成华容道:给定一种局面,华容道是否根本就无法完成,如果能完成,最少需要多少时间。
小 B 玩的华容道与经典的华容道游戏略有不同,游戏规则是这样的:
- 在一个 n*m 棋盘上有 n*m 个格子,其中有且只有一个格子是空白的,其余 n*m-1 个格子上每个格子上有一个棋子,每个棋子的大小都是 1*1 的;
- 有些棋子是固定的,有些棋子则是可以移动的;
- 任何与空白的格子相邻(有公共的边)的格子上的棋子都可以移动到空白格子上。 游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
给定一个棋盘,游戏可以玩 q 次,当然,每次棋盘上固定的格子是不会变的,但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候,空白的格子在第 EX_i 行第 EY_i 列,指定的可移动棋子的初始位置为第 SX_i 行第 SY_i 列,目标位置为第 TX_i 行第 TY_i 列。
假设小 B 每秒钟能进行一次移动棋子的操作,而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间,或者告诉他不可能完成游戏。
输入描述 Input Description
第一行有 3 个整数,每两个整数之间用一个空格隔开,依次表示 n、m 和 q;
接下来的 n 行描述一个 n*m 的棋盘,每行有 m 个整数,每两个整数之间用一个空格隔开,每个整数描述棋盘上一个格子的状态,0 表示该格子上的棋子是固定的,1 表示该格子上的棋子可以移动或者该格子是空白的。
接下来的 q 行,每行包含 6 个整数依次是 EX_i、EY_i、SX_i、SY_i、TX_i、TY_i,每两个整数之间用一个空格隔开,表示每次游戏空白格子的位置,指定棋子的初始位置和目标位置。
输出描述 Output Description
输出有 q 行,每行包含 1 个整数,表示每次游戏所需要的最少时间,如果某次游戏无法完成目标则输出 - 1。
样例输入 Sample Input
3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2
样例输出 Sample Output
2
-1
数据范围及提示 Data Size & Hint
【样例说明】
棋盘上划叉的格子是固定的,红色格子是目标位置,圆圈表示棋子,其中绿色圆圈表示目标棋子。
第一次游戏,空白格子的初始位置是 (3, 2)(图中空白所示),游戏的目标是将初始位置在 (1, 2) 上的棋子(图中绿色圆圈所代表的棋子)移动到目标位置 (2, 2)(图中红色的格子)上。
移动过程如下:

第二次游戏,空白格子的初始位置是(1, 2)(图中空白所示),游戏的目标是将初始位置在(2, 2)上的棋子(图中绿色圆圈所示)移动到目标位置 (3, 2) 上。

要将指定块移入目标位置,必须先将空白块移入目标位置,空白块要移动到目标位置,必然是从位置(2,2)上与当前图中目标位置上的棋子交换位置,之后能与空白块交换位置的只有当前图中目标位置上的那个棋子,因此目标棋子永远无法走到它的目标位置,游戏无法完成。
【数据范围】
对于 30% 的数据,1 ≤ n, m ≤ 10,q = 1;
对于 60% 的数据,1 ≤ n, m ≤ 30,q ≤ 10;
对于 100% 的数据,1 ≤ n, m ≤ 30,q ≤ 500。
——————————————————————————————————————————————————————————————————————————
思路一(虽然没错但是会 TLE)
一看到题目,联想到以前做过的八数码。于是可以想到把空白块当作可以自由移动的单位进行 BFS。由于想不到什么优化措施,所以就敲了一段大爆搜…… 虽然 TLE 是意料之中,但是没想到竟然能拿到 70 分(那这就说明我离正解不远了 / 误)
 蒟蒻的大爆搜就别看了 qwq
蒟蒻的大爆搜就别看了 qwq
——————————————————————————————————————————————————————————————————————————
思路二(正解)
整理一下为什么思路一的 BFS 是错的。
在一个规模较小的数据范围内,思路一的 BFS 是可以在 1s 内得出结论的…… 但是很不幸,虽然出题人很善良的给了 70 分(是不是没卡掉),但是爆搜还是没有前途的;
思路一的 BFS 缺陷就是,白块是以一种玄妙不可预测的路线行进的(误)。在搜索的时候会浪费很多时间在根本不可能的情况上(不做无法实现的梦)。
所以在冥 (ming) 思 (le) 苦 (ti) 想 (jie) 以后想到了绝妙的算法!
对于最优的操作,有一个前提是空白块一定要先移动到钦点块的旁边。然后空白块和钦点块再作为一个整体移动。
空白块和钦点块的移动可以用 SPFA 来求最短路径。建图的方法就是把空白块和钦点块的位置的状态看作一个点,再把每个状态之间互相转换的过程看作边,在这个图里跑一边 SPFA 就可以轻松求出正解!
以下是蒟蒻敲了一个下午的代码


1 #include<iostream>
2 #include<cstdio>
3 #include<queue>
4 #include<cstring>
5 using namespace std;
6 #define MAXN 31
7 #define MAXM 40001
8 #define INF 0x3f3f3f3f
9 int n,m,q,num[MAXN][MAXN][5],tot,cnt,head[MAXM],vis[MAXN][MAXN],ex,ey,sx,sy,tx,ty,dis[MAXM],used[MAXM],mp[MAXN][MAXN];
10 const int dx[]={1,-1,0,0},dy[]={0,0,1,-1};
11 struct Edge
12 {
13 int to,dis,next;
14 }e[MAXM];
15 struct ZT{int x,y,steps;};
16 void add(int from,int to,int dis)
17 {
18 e[++cnt].next=head[from];
19 e[cnt].to=to;
20 e[cnt].dis=dis;
21 head[from]=cnt;
22 }
23 int bfs(int ax,int ay,int bx,int by,int cx,int cy)
24 {
25 if(ax==bx&&ay==by) return 0;
26 memset(vis,0,sizeof(vis));
27 queue<ZT>Q;
28 while(!Q.empty()) Q.pop();
29 Q.push((ZT){ax,ay,0});
30 vis[ax][ay]=vis[cx][cy]=1;
31 while(!Q.empty())
32 {
33 ZT u=Q.front();Q.pop();
34 if(u.x==bx&&u.y==by) return u.steps;
35 for(int i=0;i<4;i++)
36 {
37 int x=u.x+dx[i],y=u.y+dy[i];
38 if(x>=1&&x<=n&&y>=1&&y<=m&&mp[x][y]&&!vis[x][y])
39 {
40 Q.push((ZT){x,y,u.steps+1});
41 vis[x][y]=1;
42 if(x==bx&&y==by) return u.steps+1;
43 }
44 }
45 }
46 return INF;
47 }
48 void init()
49 {
50 for(int i=1;i<=n;i++)
51 for(int j=1;j<=m;j++)
52 for(int k=0;k<4;k++)
53 if(mp[i][j]&&mp[i+dx[k]][j+dy[k]])
54 num[i][j][k]=++tot;
55 for(int i=1;i<=n;i++)
56 for(int j=1;j<=m;j++)
57 for(int k=0;k<4;k++)
58 if(num[i][j][k])
59 add(num[i][j][k],num[i+dx[k]][j+dy[k]][k^1],1);
60 for(int i=1;i<=n;i++)
61 for(int j=1;j<=m;j++)
62 for(int k=0;k<4;k++)
63 for(int l=0;l<4;l++)
64 if(l!=k&&num[i][j][k]&&num[i][j][l])
65 add(num[i][j][k],num[i][j][l],bfs(i+dx[k],j+dy[k],i+dx[l],j+dy[l],i,j));
66 }
67 int spfa()
68 {
69 queue<int>Q;
70 if(sx==tx&&sy==ty) return 0;
71 for(int i=1;i<=tot;i++) dis[i]=INF;
72 for(int k=0;k<4;k++)
73 {
74 if(num[sx][sy][k])
75 {
76 dis[num[sx][sy][k]]=bfs(ex,ey,sx+dx[k],sy+dy[k],sx,sy);
77 Q.push(num[sx][sy][k]);
78 }
79 }
80 while(!Q.empty())
81 {
82 int u=Q.front();Q.pop();
83 used[u]=0;
84 for(int i=head[u];i;i=e[i].next)
85 {
86 int v=e[i].to;
87 if(dis[v]>dis[u]+e[i].dis)
88 {
89 dis[v]=dis[u]+e[i].dis;
90 if(!used[v])
91 {
92 Q.push(v);
93 used[v]=1;
94 }
95 }
96 }
97 }
98 int ans=INF;
99 for(int k=0;k<4;k++)
100 {
101 if(num[tx][ty][k]) ans=min(ans,dis[num[tx][ty][k]]);
102 }
103 return ans==INF?-1:ans;
104 }
105 int main()
106 {
107 scanf("%d%d%d",&n,&m,&q);
108 for(int i=1;i<=n;i++)
109 for(int j=1;j<=m;j++)
110 scanf("%d",&mp[i][j]);
111 init();
112 while(q--)
113 {
114 scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty);
115 printf("%d\n",spfa());
116 }
117 return 0;
118 }
这道题做的我要死了 orz
顺便吐槽一下为什么 NOIP2013D2 前两道都是普及的水题,到最后一道题就这么难 orz

6359. 【NOIP2019 模拟 2019.9.15】小 ω 的树 (tree)(定期重构)
题目描述
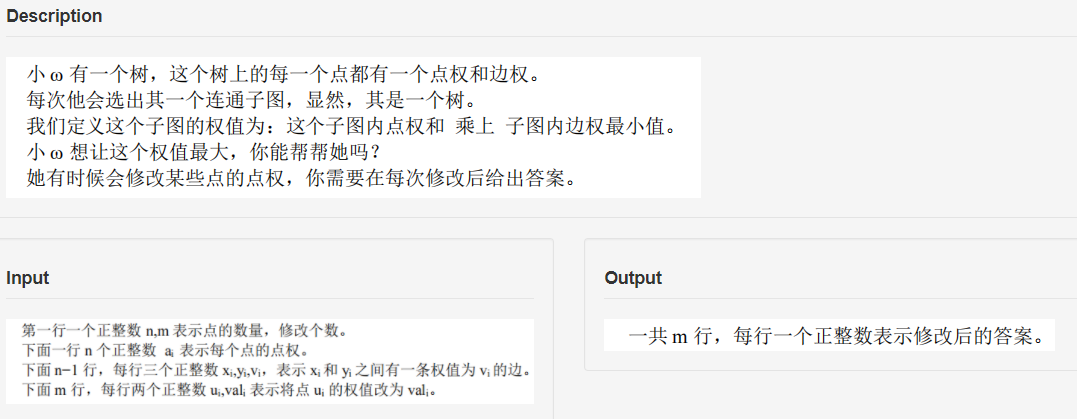
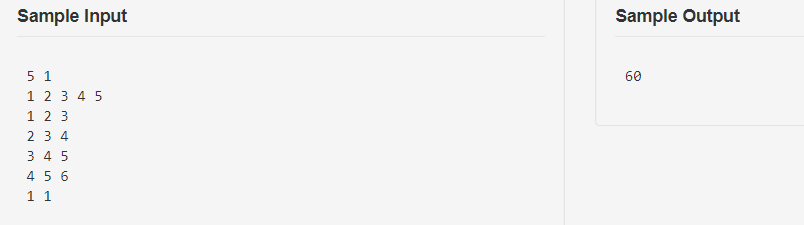
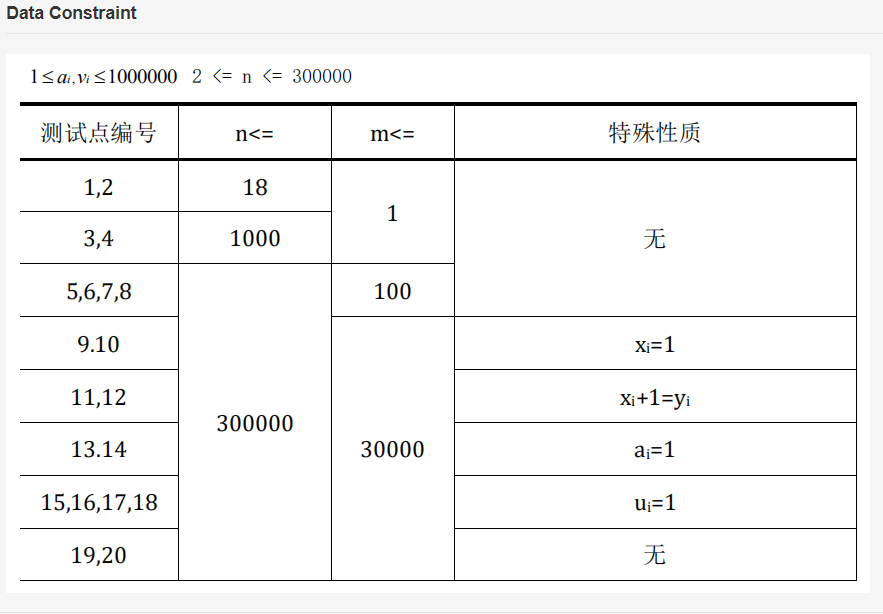
题解
qy 的毒瘤题
CSP 搞这种码农题当场手撕出题人
先按照边权从大到小建重构树,然后 40% 暴力修改 + 查找即可
100% 可以定期重构 + 平衡规划,每次把 B 个询问拉出来建虚树,在虚树上暴力维护每一段的凸壳,在凸壳上二分
虚树建法:
按照 dfs 序排序,每次用栈维护从根到当前点的栈
每次把当前点和栈顶做 lca,若 lca = 栈顶就直接加,否则一直弹到栈顶是 lca 的祖先,顺便记录下每个点在虚树上的父亲
如果栈顶 = 之前的 lca 就不用管,否则加上 lca,修改最后弹出的点的父亲
(注意要把根加进去)
设每次搞 B 个询问,那么时间为 $O (QB\log n+\frac {Qn}{B})$,极限数据下函数长这样:
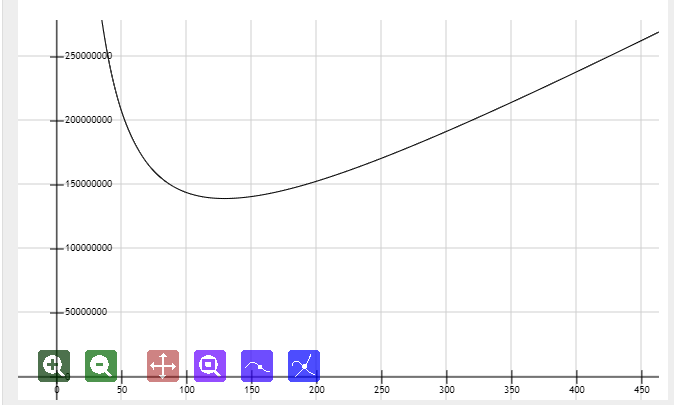
可以看出,实际最优的 B 为 $\sqrt {\frac {n}{\log n}}$,但由于常数等原因这样取会被卡成 SB
所以 B 取 $\sqrt {n}$ 就可以过了(
code
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define inc(x,y) (bg[x]<=bg[y] && ed[y]<=ed[x])
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
using namespace std;
struct type{
int x,y,s;
} b[300001];
struct Type{
int x,s,id;
} A[30001];
int c[600001];
int C[2001];
long long d[600001][2];
double dx[600001];
int l2[600001];
int r2[600001];
int w[600001];
int v[600001]; //bian
long long sum[600001];
int fa[600001][20];
int fa2[600001];
int son[600001][2];
int bg[600001];
int ed[600001];
int D[600001];
int Fa[600001];
long long ans[30001];
bool bz[600001];
int p[2001];
long long X[600001];
long long ANS[600001];
int d2[600001][2];
bool Bz[600001];
int n,Q,B,i,j,k,l,N,L,R,T,I,tot;
long long Ans,S;
bool cmp(type a,type b)
{
return a.s>b.s;
}
bool Cmp(Type a,Type b)
{
return bg[a.x]<bg[b.x];
}
bool Cmp2(Type a,Type b)
{
return a.id<b.id;
}
int gf(int t)
{
int i,t2;
t2=0;
while (Fa[t]!=t)
{
d2[++t2][0]=t;
t=Fa[t];
}
fo(i,1,t2)
Fa[d2[i][0]]=t;
return t;
}
void dfs()
{
int i,j,k,l,T,t2;
t2=1;
d2[1][0]=N;
d2[1][1]=0;
while (t2)
{
T=t2;
if (!d2[t2][1])
{
D[d2[t2][0]]=D[fa[d2[t2][0]][0]]+1;
bg[d2[t2][0]]=++j;
fo(i,1,19)
fa[d2[t2][0]][i]=fa[fa[d2[t2][0]][i-1]][i-1];
}
if (d2[t2][1]<=1)
{
if (son[d2[t2][0]][d2[t2][1]])
{
++t2;
d2[t2][0]=son[d2[T][0]][d2[T][1]];
d2[t2][1]=0;
}
++d2[T][1];
}
else
{
ed[d2[t2][0]]=j;
--t2;
}
}
}
void swap(int &x,int &y)
{
int z=x;
x=y;
y=z;
}
int lca(int x,int y)
{
int i;
if (D[x]<D[y]) swap(x,y);
fd(i,19,0)
if (D[fa[x][i]]>=D[y])
x=fa[x][i];
fd(i,19,0)
if (fa[x][i]!=fa[y][i])
{
x=fa[x][i];
y=fa[y][i];
}
if (x!=y) x=fa[x][0];
return x;
}
void init()
{
int i,j,k,l;
scanf("%d%d",&n,&Q);//B=floor(sqrt((n+n)/(log(n)/log(2)+1)));
B=floor(sqrt(n));
fo(i,1,n)
scanf("%d",&w[i]);
fo(i,1,n-1)
scanf("%d%d%d",&b[i].x,&b[i].y,&b[i].s);
sort(b+1,b+(n-1)+1,cmp);
fo(i,1,n+n-1)
Fa[i]=i;
fo(i,1,n)
sum[i]=w[i];
fo(i,1,n-1)
{
sum[n+i]=sum[gf(b[i].x)]+sum[gf(b[i].y)];
fa[Fa[b[i].x]][0]=n+i;
fa[Fa[b[i].y]][0]=n+i;
son[n+i][0]=Fa[b[i].x];
son[n+i][1]=Fa[b[i].y];
Fa[Fa[b[i].x]]=n+i;
Fa[Fa[b[i].y]]=n+i;
v[n+i]=b[i].s;
}
}
void build() //xushu
{
int i,j,k,l;
sort(A+L,A+R+1,Cmp);
l=1;
p[1]=N,bz[N]=1;
fo(i,L,R)
if (!l || p[l]!=A[i].x)
{
if (!l)
p[++l]=A[i].x;
else
{
k=lca(p[l],A[i].x);
if (k==p[l])
p[++l]=A[i].x,bz[p[l]]=1;
else
{
while (l && !inc(p[l],k))
{
fa2[p[l]]=p[l-1];
--l;
}
if (p[l]!=k)
{
fa2[p[l+1]]=k;
p[++l]=k,bz[k]=1;
}
}
p[++l]=A[i].x,bz[A[i].x]=1;
}
}
fd(i,l,1)
fa2[p[i]]=p[i-1];
sort(A+L,A+R+1,Cmp2);
tot=0;
fo(i,1,N)
if (bz[i])
C[++tot]=i;
}
void dfs2() //others
{
int i,T,t2;
t2=1;
d2[1][0]=N;
d2[1][1]=0;
while (t2)
{
T=t2;
if (!d2[t2][1])
Bz[d2[t2][0]]=bz[d2[t2][0]];
if (d2[t2][1]<=1)
{
if (son[d2[t2][0]][d2[t2][1]])
{
++t2;
d2[t2][0]=son[d2[T][0]][d2[T][1]];
d2[t2][1]=0;
}
++d2[T][1];
}
else
{
if (!Bz[d2[t2][0]])
Ans=max(Ans,sum[d2[t2][0]]*v[d2[t2][0]]);
if (t2>1)
Bz[d2[t2-1][0]]|=Bz[d2[t2][0]];
--t2;
}
}
}
long long find(int t,int x)
{
int i;
long long ans=0;
fo(i,l2[t],r2[t])
ans=max(ans,d[i][0]*x+d[i][1]);
if (l2[t]>r2[t]) return 0;
if (l2[t]==r2[t]) return d[l2[t]][0]*x+d[l2[t]][1];
int l=l2[t],r=r2[t]-1,mid;
while (l<r)
{
mid=(l+r)/2;
if (dx[mid]<=x)
l=mid+1;
else
r=mid;
}
if (dx[l]<=x)
++l;
return d[l][0]*x+d[l][1];
}
void Init() //zhixian
{
int I,i,j,k,l=0;
long long K,B;
fo(I,1,tot)
{
i=C[I];
l2[i]=l+1;
T=0;
if (i>n)
{
T=1;
c[1]=i;
j=fa[i][0];
while (j && !bz[j])
{
c[++T]=j;
j=fa[j][0];
}
}
else
{
j=fa[i][0];
while (j && !bz[j])
{
c[++T]=j;
j=fa[j][0];
}
}
fd(j,T,1)
{
if (l2[i]>l)
{
++l;
d[l][0]=v[c[j]];
d[l][1]=sum[c[j]]*v[c[j]];
}
else
{
K=v[c[j]];
B=sum[c[j]]*v[c[j]];
while (l2[i]<l && dx[l-1]*K+B>=dx[l-1]*d[l][0]+d[l][1])
--l;
if (d[l][0]!=K)
{
++l;
d[l][0]=K;
d[l][1]=B;
dx[l-1]=(double)(d[l][1]-d[l-1][1])/(d[l-1][0]-d[l][0]);
}
}
}
r2[i]=l;
ANS[i]=find(i,0);
}
}
void work(int t)
{
while (t)
{
X[t]+=S;
ANS[t]=find(t,X[t]);
t=fa2[t];
}
}
void find()
{
int i;
fo(i,1,tot)
ans[A[I].id]=max(ans[A[I].id],ANS[C[i]]);
}
void Build()
{
int i,T,t2;
t2=1;
d2[1][0]=N;
d2[1][1]=0;
while (t2)
{
T=t2;
if (!d2[t2][1])
sum[d2[t2][0]]=w[d2[t2][0]];
if (d2[t2][1]<=1)
{
if (son[d2[t2][0]][d2[t2][1]])
{
++t2;
d2[t2][0]=son[d2[T][0]][d2[T][1]];
d2[t2][1]=0;
}
++d2[T][1];
}
else
{
if (!Bz[d2[t2][0]])
Ans=max(Ans,sum[d2[t2][0]]*v[d2[t2][0]]);
if (t2>1)
sum[d2[t2-1][0]]+=sum[d2[t2][0]];
--t2;
}
}
}
int main()
{
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
init();
N=n+n-1;
j=0;
dfs();
fo(i,1,Q)
scanf("%d%d",&A[i].x,&A[i].s),A[i].id=i;
for (L=1; L<=Q; L+=B)
{
Ans=0;
tot=0;
T=0;
R=min(L+B-1,Q);
build();
dfs2();
Init();
fo(I,L,R)
{
ans[A[I].id]=Ans;
S=A[I].s-w[A[I].x];
work(A[I].x);
find();
w[A[I].x]=A[I].s;
}
Build();
fo(i,1,tot)
bz[C[i]]=0,X[C[i]]=0;
}
fo(i,1,Q)
printf("%lld\n",ans[i]);
fclose(stdin);
fclose(stdout);
return 0;
}

BZOJ 4326: NOIP2015 运输计划
传送门
Description
Input
Output
输出文件只包含一个整数,表示小 P 的物流公司完成阶段性工作所需要的最短时间。
Sample Input
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5
Sample Output
将第 1 条航道改造成虫洞: 则三个计划耗时分别为:11,12,11,故需要花费的时间为 12。
将第 2 条航道改造成虫洞: 则三个计划耗时分别为:7,15,11,故需要花费的时间为 15。
将第 3 条航道改造成虫洞: 则三个计划耗时分别为:4,8,11,故需要花费的时间为 11。
将第 4 条航道改造成虫洞: 则三个计划耗时分别为:11,15,5,故需要花费的时间为 15。
将第 5 条航道改造成虫洞: 则三个计划耗时分别为:11,10,6,故需要花费的时间为 11。
故将第 3 条或第 5 条航道改造成虫洞均可使得完成阶段性工作的耗时最短,需要花费的时间为 11。


#include <bits/stdc++.h>
using namespace std;
inline int read() {
int x = 0, f = 1; char ch = getchar();
while (ch < ''0'' || ch > ''9'') { if (ch == ''-'') f = -1; ch = getchar(); }
while (ch >= ''0'' && ch <= ''9'') { x = x * 10 + ch - 48; ch = getchar(); }
return x * f;
}
const int N = 3e5 + 10;
struct E { int ne, v, f; } e[N << 1], q[N << 1];
struct length { int u, v, len, lca; } ans[N];
int head[N], headq[N], cnt, n, m, maxlen, s[N], num, ret, fa[N], dis[N], a[N];
bool vis[N];
inline void add(int u, int v, int f) {
e[++cnt].v = v; e[cnt].f = f; e[cnt].ne = head[u]; head[u] = cnt;
}
inline void addq(int u, int v) {
q[++cnt].v = v; q[cnt].ne = headq[u]; headq[u] = cnt;
}
int getfa(int x) { return x == fa[x] ? fa[x] : fa[x] = getfa(fa[x]); }
void tarjan(int u) {
fa[u] = u;
vis[u] = 1;
for (int i = head[u]; i; i = e[i].ne) {
int v = e[i].v;
if (vis[v]) continue;
dis[v] = dis[u] + e[i].f;
tarjan(v);
a[v] = e[i].f;
fa[v] = u;
}
for (int i = headq[u]; i; i = q[i].ne) {
int v = q[i].v;
if (vis[v]) {
ans[(i + 1) / 2].lca = getfa(v);
ans[(i + 1) / 2].len = dis[u] + dis[v] - 2 * dis[ans[(i + 1) / 2].lca];
maxlen = max(maxlen, ans[(i + 1) / 2].len);
}
}
}
void dfs(int u, int pre) {
for (int i = head[u]; i; i = e[i].ne) {
int v = e[i].v;
if (v == pre) continue;
dfs(v, u);
s[u] += s[v];
}
if (s[u] == num && a[u] > ret) ret = a[u];
}
bool check(int mid) {
memset(s, 0, sizeof(s));
num = ret = 0;
for (int i = 1; i <= m; i++) {
if (ans[i].len > mid) {
num++;
s[ans[i].u]++;
s[ans[i].v]++;
s[ans[i].lca] -= 2;
}
}
dfs(1, 0);
return maxlen - ret <= mid;
}
int main() {
n = read(), m = read();
for (int i = 0; i < n - 1; i++) {
int u = read(), v = read(), f = read();
add(u, v, f);
add(v, u, f);
}
for (int i = 1; i <= n; i++) fa[i] = i;
cnt = 0;
for (int i = 1; i <= m; i++) {
int u = read(), v = read();
ans[i].u = u; ans[i].v = v;
addq(u, v); addq(v, u);
}
tarjan(1);
int l = 0, r = maxlen;
while (l + 1 < r) {
int mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
printf("%d\n", r);
return 0;
}

BZOJ 4326: NOIP2015 运输计划 (二分,树上差分)
Time Limit: 30 Sec Memory Limit: 128 MBSubmit: 1945 Solved: 1243
[Submit][Status][Discuss]
Description
Input
Output
输出文件只包含一个整数,表示小 P 的物流公司完成阶段性工作所需要的最短时间。
Sample Input
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5
Sample Output
将第 1 条航道改造成虫洞: 则三个计划耗时分别为:11,12,11,故需要花费的时间为 12。
将第 2 条航道改造成虫洞: 则三个计划耗时分别为:7,15,11,故需要花费的时间为 15。
将第 3 条航道改造成虫洞: 则三个计划耗时分别为:4,8,11,故需要花费的时间为 11。
将第 4 条航道改造成虫洞: 则三个计划耗时分别为:11,15,5,故需要花费的时间为 15。
将第 5 条航道改造成虫洞: 则三个计划耗时分别为:11,10,6,故需要花费的时间为 11。
故将第 3 条或第 5 条航道改造成虫洞均可使得完成阶段性工作的耗时最短,需要花费的时间为 11。
HINT
Source
考场上没想出来怎么求一条边被覆盖的次数。
后来看了题解,发现要用树上差分
然后自己 yy 了一个:LCA 出 $+1$, 两个节点 $-1$,但是如果是链的话这样会被卡掉
正确做法是 LCA 处 $-2$,两个节点 $+1$,然后从底向上更新
这样的话这道题就很简单了
我们要求路径的最大值最小,
可以二分这个最小值
然后判断树上是否存在一条边,被比当前值大的链都覆盖到
// luogu-judger-enable-o2
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
char buf[1 << 21], *p1 = buf, *p2 = buf;
//#define int long long
using namespace std;
const int MAXN = 3 * 1e5 + 10;
inline int read() {
char c = getchar(); int x = 0, f = 1;
while(c < ''0'' || c > ''9'') {if(c == ''-'') f = -1; c = getchar();}
while(c >= ''0'' && c <= ''9'') x = x * 10 + c - ''0'', c = getchar();
return x * f;
}
struct Edge {
int u, v, w, nxt;
}E[MAXN << 1];
int head[MAXN], num = 0;
inline void AddEdge(int x, int y, int z) {
E[num] = (Edge){x, y, z, head[x]};
head[x] = num++;
}
struct Plan {
int bg, ed, lca, val;
bool operator < (const Plan &rhs) const {
return val < rhs.val;
}
}P[MAXN];
int N, M;
int sum[MAXN], deep[MAXN], top[MAXN], siz[MAXN], son[MAXN], fa[MAXN], dfn[MAXN], Pval[MAXN];
void dfs1(int x, int f) {
fa[x] = f; siz[x] = 1; dfn[++dfn[0]] = x;
for(int i = head[x]; i != -1; i = E[i].nxt) {
if(!deep[E[i].v]) {
deep[E[i].v] = deep[x] + 1;
sum[E[i].v] = sum[x] + E[i].w;
Pval[E[i].v] = E[i].w;
dfs1(E[i].v, x);
siz[x] += siz[E[i].v];
if(siz[E[i].v] > siz[son[x]]) son[x] = E[i].v;
}
}
}
int LCA(int x, int y) {
while(top[x] != top[y]) {
if(deep[top[x]] < deep[top[y]]) swap(x, y);
x = fa[top[x]];
}
if(deep[x] < deep[y]) swap(x, y);
return y;
}
int tag[MAXN], happen[MAXN << 1];
int check(int tim) {
int pos = upper_bound(P + 1, P + M + 1, (Plan){0, 0, 0, tim}) - P;
memset(tag, 0, sizeof(tag));
for(int i = pos; i <= M; i++) tag[P[i].bg]++, tag[P[i].ed]++, tag[P[i].lca] -= 2;//树上差分求每个边被经过的次数。
for(int i = N; i >= 1; i--) {
tag[fa[dfn[i]]] += tag[dfn[i]];
if(P[M].val - Pval[dfn[i]] <= tim && tag[dfn[i]] >= M - pos + 1) return 1;
}
return 0;
}
int l, r;
int Solve() {
int ans = 1e9 + 10;
l = r - l;
while(l <= r) {
int mid = l + r >> 1;
if(check(mid)) ans = mid, r = mid - 1;
else l = mid + 1;
}
return ans;
}
int main() {
#ifdef WIN32
freopen("a.in", "r", stdin);
#endif
//printf("%lf\n", log2(12345));
memset(head, -1, sizeof(head));
N = read(); M = read();
for(int i = 1; i <= N - 1; i++) {
int x = read(), y = read(), z = read();
AddEdge(x, y, z); AddEdge(y, x, z);
l = max(l, z);
}
deep[1] = 1; dfs1(1, 0);
top[1] = 1;
for(int i = 1; i <= N; i++)
top[dfn[i]] = dfn[i] == son[fa[dfn[i]]] ? top[fa[dfn[i]]] : dfn[i];
for(int i = 1; i <= M; i++) {
P[i].bg = read(), P[i].ed = read();
P[i].lca = LCA(P[i].bg, P[i].ed);
P[i].val = sum[P[i].bg] + sum[P[i].ed] - 2 * sum[P[i].lca];
r = max(r, P[i].val);
}
sort(P + 1, P + M + 1);
printf("%d", Solve());
return 0;
}
关于NOIP2015 T4 推销员和推销员door to door2002的问题就给大家分享到这里,感谢你花时间阅读本站内容,更多关于2018/7/16 YMOI 模拟 NOIP2013D2T3 华容道、6359. 【NOIP2019 模拟 2019.9.15】小 ω 的树 (tree)(定期重构)、BZOJ 4326: NOIP2015 运输计划、BZOJ 4326: NOIP2015 运输计划 (二分,树上差分)等相关知识的信息别忘了在本站进行查找喔。
本文标签:





