对于双“11”搞促销?用贪心算法来盘他!感兴趣的读者,本文将提供您所需要的所有信息,并且为您提供关于3.贪心算法、diikstra是贪心算法吗_哪些算法是贪心算法、Java函数中如何应用贪心算法优化?
对于双“11”搞促销?用贪心算法来盘他!感兴趣的读者,本文将提供您所需要的所有信息,并且为您提供关于3.贪心算法、diikstra是贪心算法吗_哪些算法是贪心算法、Java 函数中如何应用贪心算法优化?、JS使用贪心算法解决找零问题示例的宝贵知识。
本文目录一览:
双“11”搞促销?用贪心算法来盘他!

作者 | 王磊
来源 | Java中文社群(ID:javacn666)
这几年商家为了刺激消费是变着花样的推出各种各样的活动,以某多多为首的运营式电商更是让我们看到了营销的无限“潜力”。
这不,最近刚赶上双 11,小区便利店的老王头也推出了一项「空酒瓶子换酒」的促销活动,它的规则是这样的。
本文已收录至 Github《小白学算法》系列:https://github.com/vipstone/algorithm
活动规则
客户购买 X 瓶酒,就可以用 Y 个空酒瓶来兑换一瓶新酒。
提示:
X 和 Y 的取值如下:
1 <= X <= 100 2 <= Y <= 100 Y 值不固定,随机抽取。
如果喝掉了酒瓶中的酒,那么酒瓶就会变成空的。
请你计算最多能喝到多少瓶酒。
示例 1:
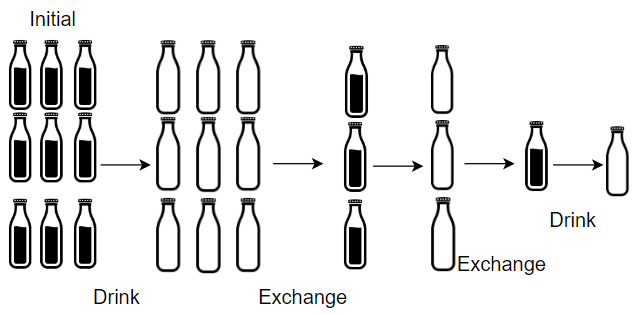
输入:X = 9, Y = 3
输出:13
解释:你可以用 3 个空酒瓶兑换 1 瓶酒。所以最多能喝到 9 + 3 + 1 = 13 瓶酒。
示例 2:
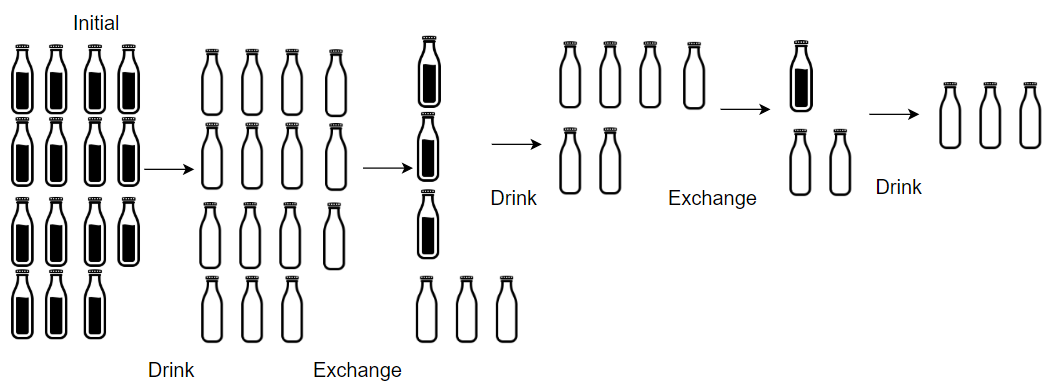
输入:X = 15, Y = 4
输出:19
解释:你可以用 4 个空酒瓶兑换 1 瓶酒。所以最多能喝到 15 + 3 + 1 = 19 瓶酒。
示例 3:
输入:X = 5, Y = 5
输出:6
示例 4:
输入:X = 2, Y = 3
输出:2
解题思路
这道题难点有两个:第一,用多少个空瓶换一瓶酒是不固定的(随机的);第二,兑换的酒喝完之后还能继续参与兑换活动。因此要在满足这两个的前提条件下,计算自己最多能喝到几瓶。
可能有些朋友看到了本篇标题之后就知道了解题思路,没错,我们本文就是要用「贪心算法」来计算最终答案。同时这道题也符合贪心算法的解题思路,那就是有酒瓶就兑换、能兑换多少就兑换多少。
贪心算法
贪心算法(Greedy Algorithm),又称贪婪算法,是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是局部最优解能决定全局最优解。简单地说,问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
贪心算法的实现框架
从问题的初始解出发:
while(能朝给定总目标前进一步)
{
利用可行的决策,求出一个可行解元素;
}
由所有解元素组合成问题的一个可行解。
注意:因为用贪心算法只能通过解局部最优解的策略来达到全局最优解,因此,一定要注意判断问题是否适合采用贪心算法策略,找到的解是否一定是问题的最优解。
接下来我们就用代码来演示一下贪心算法的具体实现。
代码实现 1:贪心
首先我们先把全局问题转换成局部问题:当空瓶子能换一瓶酒的时候,我们就换一瓶酒,实现代码如下:
// 贪心1:用 + 和 - 实现
class Solution {
public int numWaterBottles(int numBottles, int numExchange) {
// 最大酒瓶数
int total = numBottles;
// 有酒瓶就兑换
while (numBottles >= numExchange) {
// 执行一轮兑换
numBottles -= numExchange;
++total;
// 兑换一次多一个酒瓶
++numBottles;
}
return total;
}
}
代码解析
实现思路:
-
先把所有酒喝掉 int total = numBottles; -
有足够的空瓶就去换一瓶酒,执行一次 while循环; -
在循环中,空瓶的数量 +1,能喝到酒的数量 +1; -
执行下一次循环判断。
我们将以上代码提交至 LeetCode,执行结果如下:
代码实现 2:贪心改进
以上的贪心算法是一瓶酒一瓶酒进行循环兑换的,那我们可否每次将所有的空瓶子全部兑换完(可兑换的最大值),然后将兑换的酒再喝完,再进行下一次兑换?
答案是肯定的,我们只需要使用取模和取余操作就可以实现了,具体代码如下:
// 贪心 2:用 / 和 % 实现
class Solution {
public int numWaterBottles(int numBottles, int numExchange) {
// 总酒瓶数
int total = numBottles;
// 有酒瓶就兑换
while (numBottles >= numExchange) {
// 最多可兑换的新酒
int n = numBottles / numExchange;
// 累计酒瓶
total += n;
// 剩余酒瓶(剩余未兑换 + 已兑换喝掉的)
numBottles = numBottles % numExchange + n;
}
return total;
}
}
我们将以上代码提交至 LeetCode,执行结果如下:
总结
贪心算法初看感觉很“难”,但具体实现起来却发现很简单。其实「算法」也是一样的,初看这个词感觉很难很高大上,其实它就是解决某个问题的一种思想、一种固定的“套路”而已,也并无神秘可言。
人常说:路虽远行则将至,事虽然难做者必成。“难”和“易”从来都是相对的,其实从“难”到“易”就是一个逐渐开悟、逐渐成长的过程。
愿你每天成长一点,最后留一个我的私人微信:GG_Stone,相互交流、共同进步。
参考 & 鸣谢

往期推荐

嗯,查询滑动窗口最大值的这4种方法不错....

小白学算法:买卖股票的最佳时机!

23张图!万字详解「链表」,从小白到大佬!
本文分享自微信公众号 - Java中文社群(javacn666)。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。

3.贪心算法
贪心算法(又称贪婪算法)
是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
基本要素
贪心选择
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。
贪心选择是采用从顶向下、以迭代的方法做出相继选择,每做一次贪心选择就将所求问题简化为一个规模更小的子问题。对于一个具体问题,要确定它是否具有贪心选择的性质,我们必须证明每一步所作的贪心选择最终能得到问题的最优解。通常可以首先证明问题的一个整体最优解,是从贪心选择开始的,而且作了贪心选择后,原问题简化为一个规模更小的类似子问题。然后,用数学归纳法证明,通过每一步贪心选择,最终可得到问题的一个整体最优解。
最优子结构
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。运用贪心策略在每一次转化时都取得了最优解。问题的最优子结构性质是该问题可用贪心算法或动态规划算法求解的关键特征。贪心算法的每一次操作都对结果产生直接影响,而动态规划则不是。贪心算法对每个子问题的解决方案都做出选择,不能回退;动态规划则会根据以前的选择结果对当前进行选择,有回退功能。动态规划主要运用于二维或三维问题,而贪心一般是一维问题。
实例
哈夫曼编码
(算法详解)
class Greedy:
def __init__(self):
pass
''''''
哈夫曼编码
''''''
class Node:
''''''
实现节点类
''''''
def __init__(self, kv):
self.left = None
self.right = None
self.father = None
self.kv = kv
def is_left(self):
if self.father is not None:
return self.father.left == self
def create_nodes(self, kvs):
''''''
为每一个节点赋值
:param kvs:
:return:
''''''
return [self.Node(kv) for kv in kvs]
def create_huffman_tree(self, nodes):
''''''
创建哈夫曼树
:param nodes:
:return: 根节点
''''''
queue = nodes[:]
while len(queue) > 1:
queue.sort(key=lambda item: item.kv[1])
node_left = queue.pop(0)
node_right = queue.pop(0)
node_father = self.Node((None, node_left.kv[1] + node_right.kv[1], None))
node_father.left = node_left
node_father.right = node_right
node_left.father = node_father
node_right.father = node_father
queue.append(node_father)
return queue[0]
def huffman_encoding(self, nodes, root):
''''''
遍历叶节点,保存路径
:param nodes:
:param root:
:return:
''''''
for i in range(len(nodes)):
node_tmp = nodes[i]
while node_tmp != root:
if node_tmp.is_left():
nodes[i].kv[2] += ''0''
else:
nodes[i].kv[2] += ''1''
node_tmp = node_tmp.father
def get_huffman_code(self, string, nodes):
''''''
哈夫曼加密
:param string:
:param nodes:
:return:
''''''
code = ''''
for character in string:
for node in nodes:
if character == node.kv[0]:
code += node.kv[2]
break
return code
def get_huffman_string(self, code, root):
''''''
哈夫曼解密
:param code:
:param root:
:return:
''''''
string = ''''
node = root
for elem in code:
if elem == ''0'':
node = node.left
if elem == ''1'':
node = node.right
if node.left is None and node.right is None:
string += node.kv[0]
node = root
return string
if __name__ == ''__main__'':
greedy = Greedy()
nodes = greedy.create_nodes([
[''A'', 5, ''''],
[''B'', 4, ''''],
[''C'', 3, ''''],
[''D'', 2, ''''],
[''E'', 1, ''''],
])
root = greedy.create_huffman_tree(nodes)
for node in nodes:
print(node.kv)
greedy.huffman_encoding(nodes, root)
for node in nodes:
print(node.kv)
code = greedy.get_huffman_code(''ACE'', nodes)
print(code)
string = greedy.get_huffman_string(code, root)
print(string)
单源最短路径(算法详解)
最小生成树(算法详解)

diikstra是贪心算法吗_哪些算法是贪心算法
否,dijkstra 算法不是贪心算法。贪心算法在每个步骤中做出局部最优选择,希望最终得到全局最优解,而 dijkstra 算法使用动态规划,通过考虑所有可能的子路径选择最短路径。其他贪心算法示例包括 kruskal 算法、prim 算法、哈夫曼编码、背包问题和贪婪着色算法。

Dijkstra 算法是贪心算法吗?
答案: 否
什么是贪心算法?
贪心算法是一种基于当前最优结果做出决策,以构建全局最优解决方案的算法。换句话说,贪心算法在每个步骤中都做出局部最优选择,希望这些选择最终导致全局最优解。
Dijkstra 算法不是贪心算法
Dijkstra 算法是一种解决加权图中单源最短路径问题的算法。它使用动态规划的方法,而不是贪心方法。在 Dijkstra 算法中,每一个子问题(找出从源点到给定顶点的最短路径)都是通过考虑所有可能的子路径并选择最短的一个来解决的。
其他贪心算法示例
- 克鲁斯卡尔算法:解决最小生成树问题的贪心算法。
- 普里姆算法:解决最小生成树问题的另一种贪心算法。
- 哈夫曼编码:解决无损数据压缩问题的贪心算法。
- 背包问题:解决在有限容量背包中装入最大价值物品问题的贪心算法。
- 贪婪着色算法:解决图着色问题的贪心算法。
以上就是diikstra是贪心算法吗_哪些算法是贪心算法的详细内容,更多请关注php中文网其它相关文章!

Java 函数中如何应用贪心算法优化?
贪心算法是一种优化问题中的决策过程,在每个子问题中做出当前最优选择,通过分解问题、做出贪心选择和设置终止条件,可在 java 函数中应用它。实战案例:背包问题,采用动态规划算法求解,通过自顶向下的决策过程,在每次迭代中做出贪心选择,并存储子问题的解,最终返回最大价值的解。

Java 函数中贪心算法的优化
贪心算法是一种广泛应用于各种优化问题的算法。它本质上是一种自顶向下的决策过程,在面临选择时,它会做出在当前情况下看来最好的选择,而不用考虑未来的影响。对于某些问题,这种策略可以产生非常好的解,即使它不能保证找到最优解。
为了在 Java 函数中应用贪心算法进行优化,可以遵循以下步骤:
立即学习“Java免费学习笔记(深入)”;
1. 确定问题
首先,需要清楚地定义要解决的问题。确定目标函数或需要优化的指标非常重要。
2. 分解问题
将问题分解成更小的子问题,这样可以更容易地采用贪心策略。在每个子问题中应用贪心选择。
3. 做出贪心选择
在每个子问题中,根据当前状态做出贪心选择。有多种贪心选择的策略,例如选择当前最优的项或选择带来最大近期收益的项。
4. 终止条件
确定算法的终止条件,当所有子问题都已解决或不再有可行的贪心选择时,算法将停止。
实战案例:求解背包问题
背包问题是一个经典的优化问题,其中目标是将一组物品装入容量有限的背包中,使总价值最大化。
Java 代码:
import java.util.Arrays;
class BackpackProblem {
static int maxProfit(int[] weights, int[] profits, int capacity) {
int[][] dp = new int[weights.length + 1][capacity + 1];
for (int i = 0; i <= weights.length; i++) {
for (int j = 0; j <= capacity; j++) {
if (i == 0 || j == 0) {
dp[i][j] = 0;
} else if (weights[i - 1] <= j) {
dp[i][j] = Math.max(dp[i - 1][j], profits[i - 1] + dp[i - 1][j - weights[i - 1]]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[weights.length][capacity];
}
public static void main(String[] args) {
int[] weights = {1, 3, 4, 5};
int[] profits = {1, 4, 5, 7};
int capacity = 7;
System.out.println("最大价值:" + maxProfit(weights, profits, capacity));
}
}在这个例子中,我们使用动态规划实现了一个贪心算法,它采用自顶向下的决策过程,在每次迭代中做出贪心选择,并将子问题的解存储在动态规划表中。最终的结果代表了最大价值的解。
以上就是Java 函数中如何应用贪心算法优化?的详细内容,更多请关注php中文网其它相关文章!

JS使用贪心算法解决找零问题示例
本文实例讲述了JS使用贪心算法解决找零问题。分享给大家供大家参考,具体如下:
前面介绍了,这里再来看看找零问题的解决方法。
在现实生活中,经常遇到找零问题,假设有数目不限的面值为20,10,5,1的硬币。 给出需要找零数,求出找零方案,要求:使用数目最少的硬币。
对于此类问题,贪心算法采取的方式是找钱时,总是选取可供找钱的硬币的最大值。比如,需要找钱数为25时,找钱方式为20+5,而不是10+10+5。
贪心算法还是很常见的算法之一,这是由于它简单易行,构造贪心策略不是很困难。
可惜的是,它需要证明后才能真正运用到题目的算法中。
"); } greedyMoney(money,73); greedyMoney([25,1],63);





