PriorityQueue：无法将学生转换为java.lang.Comparable（无法将javac项识别为怎么改）

25-02-24 16

对于想了解PriorityQueue：无法将学生转换为java.lang.Comparable的读者，本文将是一篇不可错过的文章，我们将详细介绍无法将javac项识别为怎么改，并且为您提供关于#Jav

对于想了解PriorityQueue：无法将学生转换为java.lang.Comparable的读者，本文将是一篇不可错过的文章，我们将详细介绍无法将javac项识别为怎么改，并且为您提供关于# Java Queue系列之PriorityQueue、c – 无法将派生的Compare传递给std :: priority_queue、Java - PriorityQueue、Java Collection - PriorityQueue 优先队列的有价值信息。

本文目录一览：

PriorityQueue：无法将学生转换为java.lang.Comparable（无法将javac项识别为怎么改）
# Java Queue系列之PriorityQueue
c – 无法将派生的Compare传递给std :: priority_queue
Java - PriorityQueue
Java Collection - PriorityQueue 优先队列

PriorityQueue：无法将学生转换为java.lang.Comparable（无法将javac项识别为怎么改）

我正在使用PriorityQueue结构来获取用户设置的一些字段，这是代码的一部分：

package gqg;import java.util.Queue;public class Student {     //variables (ID, Name, ...), constructors, getters and setters...Queue<Student> StudentQueue = new PriorityQueue<Student>();public void Add() { //method to add the student at Queue    for(int x=0; x<1; x++) {        Student st = new Student();        System.out.println("+---------------------------+\n"                         + "|   Students Registration   |\n"                         + "+---------------------------+");        System.out.println("| Type the student''s ID:");        stu.setID(user.nextInt());        System.out.println("| Type the student''s name:");        stu.setName(user.next());        System.out.println("| Type the student''s age:");        stu.setAge(user.nextInt());        //and other fields...        StudentQueue.add(st);    }    System.out.println("Done. Student has been added successfuly\n");       }/* then I call Add(); in Menu(); * this method also has Print(); Modify(); Eliminate(); those three works well * The only one problem is Add(); */public void Menu(){    //... methods}}

当我仅添加一个“学生”时没有问题，但是当我尝试捕获第二个“学生”时，应用程序将引发此异常

Exception in thread "main" java.lang.ClassCastException: gqg.Student cannot be cast to java.lang.Comparable     atjava.util.PriorityQueue.siftUpComparable(PriorityQueue.java:633)    atjava.util.PriorityQueue.siftUp(PriorityQueue.java:629)  atjava.util.PriorityQueue.offer(PriorityQueue.java:329)   atjava.util.PriorityQueue.add(PriorityQueue.java:306)     atgqg.Student.AddQueue(Student.java:374)  atgqg.Student.Menu(Student.java:592)  atgqg.MainClass.main(MainClass.java:7)

有人可以向我解释问题出在哪里/为什么？我花了很多时间在Web上寻找解决方案，但找不到，我在这里需要一些帮助…

答案1

小编典典

如果不提供custom
Comparator，PriorityQueue则对它持有的对象使用自然顺序。也就是说，它希望您的对象Comparable彼此之间。您的Student课程似乎没有实现Comparable。

有两个选择：

实现并提供Comparator用于比较Student对象的自定义
让您的Student班级Comparable<Student>以适当的逻辑实施

# Java Queue系列之PriorityQueue

在上一篇中我用一张图来梳理了一下Java中的各种Queue之间的关系。这里介绍下PriorityQueue。PriorityQueue位于Java util包中，观其名字前半部分的单词Priority是优先的意思，实际上这个队列就是具有“优先级”。既然具有优先级的特性，那么就得有个前后排序的“规则”。所以其接受的类需要实现Comparable 接口。

API

1.构造函数

PriorityQueue()
PriorityQueue(Collection<? extends E> c)
PriorityQueue(int initialCapacity)
PriorityQueue(int initialCapacity,Comparator<? super E> comparator)
PriorityQueue(PriorityQueue<? extends E> c)
PriorityQueue(SortedSet<? extends E> c)

2.常用功能函数

方法名	功能描述
add(E e)	添加元素
clear()	清空
contains(Object o)	检查是否包含当前参数元素
offer(E e)	添加元素
peek()	读取元素，（不删除）
poll()	取出元素，（删除）
remove(Object o)	删除指定元素
size()	返回长度

用法示例

上面提到具有优先级，那么这里举个例子。我在上高中的时候，每月分一次班级，老师会按照本月月考的成绩来让每位同学优先选择自己心仪的座位。这里所有的同学便是一个队列；每次喊一个人进来挑选座位，这便是出对的操作；成绩由前至后，这边是优先的策略。

代码示例如下：

public class PriorityQueueTest {
	public static void main(String[] args) {
        		
		final PriorityQueue<Student> queue=new PriorityQueue<>();

		Student p1=new Student(95,"张三");
		Student p2=new Student(89,"李四");
		Student p3=new Student(89,"李四");
		Student p4=new Student(67,"王五");
		Student p5=new Student(92,"赵六");
		queue.add(p1);
		queue.add(p2);
		queue.add(p3);//add 和offer效果一样。
		queue.offer(p4);//add 方法实现，其实就是调用了offer
		queue.offer(p5)

		for (Student Student : queue) {
			System.out.println(Student.toString());
		}
		
		System.out.println("---------------------");
		while(!queue.isEmpty()){
			System.out.println(queue.poll());
		} 	    
	}

}
class Student implements Comparable{
	private int score;
	private String name;
	
	public Student(int age,String name){
		this.score=age;
		this.name=name;
	}
	public int getscore() {
		return score;
	}
	public void setscore(int score) {
		this.score = score;
	}
	public String getName() {
		return name;
	}
	public void setName(String name) {
		this.name = name;
	}
	public String toString(){
		return "姓名："+name+"-"+score+"分";
	}

	@Override
	public int compareto(Object o) {
		Student current=(Student)o;
		if(current.getscore()>this.score){
			return 1;
		}else if(current.getscore()==this.score){
			return 0;
		}
		return -1;
	}
}

运行结果：
姓名：张三-95分
姓名：赵六-92分
姓名：王五-67分
姓名：李四-89分
---------按顺序出队选座位------------
姓名：张三-95分
姓名：赵六-92分
姓名：李四-89分
姓名：李四-89分
姓名：王五-67分

从第一部分输出可以看出，学生入队并不是 按顺序的，而在poll出来的时候是按顺序出队的，这里确实实现了分数高这优先选座位的效果，poll方法返回的总是队列剩余学生中分数最高的。

安全性

查看PriorityQueue类的源码，会发现增加操作，并不是原子操作。没有使用任何锁。那么，如果是在多线程环境，肯定是不安全的。下面给出例子，开启多个线程，调用同一个方法对Queue进行添加元素。然后输出结果。

public class PriorityQueueTest {

	static final PriorityQueue<Integer> queue=new PriorityQueue<>();
	/**
	 * 向队列中插入元素
	 * @param number
	 */
	public  void add(int number){
		if(!queue.contains(number)){
			System.out.println(Thread.currentThread()+"："+number);
			queue.add(number);
		}
	}	

public static void main(String[] args) throws InterruptedException {
	final PriorityQueueTest qt=new PriorityQueuetest();
		final Random r=new Random();
		Thread t1=new Thread(){
			public void run(){
				System.out.println("t1开始运行...");
				for(int i=0;i<10;i++){
					qt.add(r.nextInt(10));
				}
			}
		};
		Thread t2=new Thread(){
			public void run(){
				System.out.println("t2开始运行...");
				for(int i=0;i<10;i++){
					qt.add(r.nextInt(10));
				}
			}
		};
		Thread t3=new Thread(){
			public void run(){
				System.out.println("t3开始运行...");
				for(int i=0;i<10;i++){
					qt.add(r.nextInt(10));
				}
			}
		};
		t1.start();
		t2.start();
		t3.start();
		t1.join();
		t2.join();
		t3.join();
		System.out.println("------ 运行结果 ---------");
		while(!queue.isEmpty()){
			System.out.println(queue.poll());
		}
	}
}

运行结果
t2开始运行...
t3开始运行...
t1开始运行...
------ 运行结果 ---------
0
1
1
2
3
4
5
6
7
8
9
9

结果中我们可以看到，具有两个1，两个9.这是不符合我们预期的，我们预期的是not contains 才插入，现在的出现的了重复的。上面的例子只需要在add方法上加锁，才可以达到我们预期的效果。所以说，PriorityQueue是非线程安全的。
[1]: http://www.cnblogs.com/demingblog/p/6474865.html

工作6年，失业19天
Java8系列- 如何用Java8 Stream API找到心仪的女朋友
Java8系列- 何用Java8 Stream API进行数据抽取与收集

spring如何启动的？这里结合spring源码描述了启动过程
SpringMVC是怎么工作的,SpringMVC的工作原理
spring 异常处理。结合spring源码分析400异常处理流程及解决方法

Mybatis Mapper接口是如何找到实现类的-源码分析
使用Netty实现HTTP服务器
Netty实现心跳机制
Netty系列

c – 无法将派生的Compare传递给std :: priority_queue

我需要将派生的比较器传递给std :: priority_queue,但由于某种原因,正在调用基类’operator().

这是一个显示此行为的最小代码：

class Base {
    public:
    virtual bool operator() (int l,int r) const {
        cout << "Should not be called" << std::endl;
        return 0;
    }
    virtual ~Base() {}
};
class A : public Base { 
    public:
    bool operator() (int l,int r) const override {
        cout << "Should be called!!!!";
        return l < r;
    }
};
int main() {
    priority_queue<int,vector<int>,Base> pq((A()));
    pq.push(1);
    pq.push(2);
    pq.push(3);
    pq.push(0);
    cout << pq.top();
    return 0;
}

The code is available on ideone as well

请注意,我不能使用priority_queue< int,vector< int>,A>,因为我有Base的其他子类,这将导致大量代码重复1.

我究竟做错了什么？如何将比较器传递给将在其生命周期内使用的priority_queue？

(1)我知道我可以通过使用接受priority_queue< int,T>的模板函数来绕过代码复制问题. – 但我真的不愿意.

解决方法

该标准指定比较comp作为23.6.4.1中类模板的值成员.据说构造函数：

Initializes comp with x and c with y (copy constructing or move
constructing as appropriate);

因此你有切片,即使参数类型实际上是一个const比较&amp ;.

要解决这个问题,你可以为比较器实现一个pimpl-wrapper.这个包装器将在内部保持Base&到实际的比较器,在它的非虚拟运算符()中只需调用Base / A比较器的虚拟运算符().

请仔细考虑A对象的生命周期.根据比较器所需的状态,您可以在Base中实现virtual clone-method.并将Base保留为std :: unique_ptr< Base>在你的PimplCompare中 – 你克隆它的副本.或者你把它保存为std :: shared_ptr< Base>.

Java - PriorityQueue

JDK 10.0.2

前段时间在网上刷题，碰到一个求中位数的题，看到有网友使用PriorityQueue来实现，感觉其解题思想挺不错的。加上我之前也没使用过PriorityQueue，所以我也试着去读该类源码，并用同样的思想解决了那个题目。现在来对该类做个总结，需要注意，文章内容以算法和数据结构为中心，不考虑其他细节内容。如果小伙伴想看那个题目，可以直接跳转到（小测试）。

一. 数据结构：queue[]、size、comparator
二. 初始化（堆化）：heapify()、siftDownComparable(k, e)
三. 添加元素：offer(e)、siftUpUsingComparator(k, e)
四. 索引：indexOf(o)
五. 删除元素：remove(o)、removeAt(i)、removeEq(o)
六. 取堆顶：peek()
七. 删除堆顶：poll()
八. 清除队列：clear()
九. 遍历：iterator()、toArray()、toArray(T[] a)
十. 小测试：数据流中的中位数

一. 数据结构

我只列出了讲解需要的重要属性，不考虑其他细节。PriorityQueue（优先队列）内部是以堆来实现的。为了描述方便，接下来的内容我将用pq[ ]代替queue[ ]。

PriorityQueue<E> {
    /* 平衡二叉堆 用于存储元素
     * n : 0 -> size-1
     * pq[n].left = pq[2*n+1]
     * pq[n].right = pq[2*(n+1)]
     */
    Object[] queue; 
    int size; // pq中元素个数
    Comparator<? super E> comparator; // 自定义比较器
}

回到目录

二. 初始化（堆化）

如果使用已有集合来构造PriorityQueue，就会用到heapify()来对pq[ ]进行初始化（即：二叉堆化），使其满足堆的性质。而heapify()又通过调用siftDownComparable(k, e)来完成堆化。源码如下：

 1 @SuppressWarnings("unchecked")
 2 private void heapify() {
 3     final Object[] es = queue;
 4     int i = (size >>> 1) - 1;
 5     if (comparator == null)
 6         for (; i >= 0; i--)
 7             siftDownComparable(i, (E) es[i]);
 8     else
 9         for (; i >= 0; i--)
10             siftDownUsingComparator(i, (E) es[i]);
11 }
12 
13 @SuppressWarnings("unchecked")
14 private void siftDownComparable(int k, E x) {
15     Comparable<? super E> key = (Comparable<? super E>)x;
16     int half = size >>> 1;        // loop while a non-leaf
17     while (k < half) {
18         int child = (k << 1) + 1; // assume left child is least
19         Object c = queue[child];
20         int right = child + 1;
21         if (right < size &&
22             ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
23             c = queue[child = right];
24         if (key.compareTo((E) c) <= 0)
25             break;
26         queue[k] = c;
27         k = child;
28     }
29     queue[k] = key;
30 }

View Code

如果有自定义比较器的话，调用：siftDownUsingComparator(k, e)，否则调用：siftDownComparable(k, e)。这两个方法只是在比较两个元素大小时的表现形式不同，其他内容相同，所以我们只需要看其中一种情况就行。为了描述方便，下面的例子中，我使用Integer作为pq[ ]存储元素类型，所以调用的是siftDownComparable(k, e)。（size >>> 1 表示 size 无符号右移1位，等价于size / 2）

我不会去细抠源码，一行一行地为大家讲解，而是尽量使用简单的例子来展示，我觉得通过例子以及后期大家自己阅读源码，会更容易理解算法内容。

现在我们来看看，使用集合{2, 9, 8, 4, 7, 1, 3, 6, 5}来构造PriorityQueue的过程。算法时间复杂度为O(n)，n = size。（时间复杂度证明：《算法导论》（第3版）第6章6.3建堆）

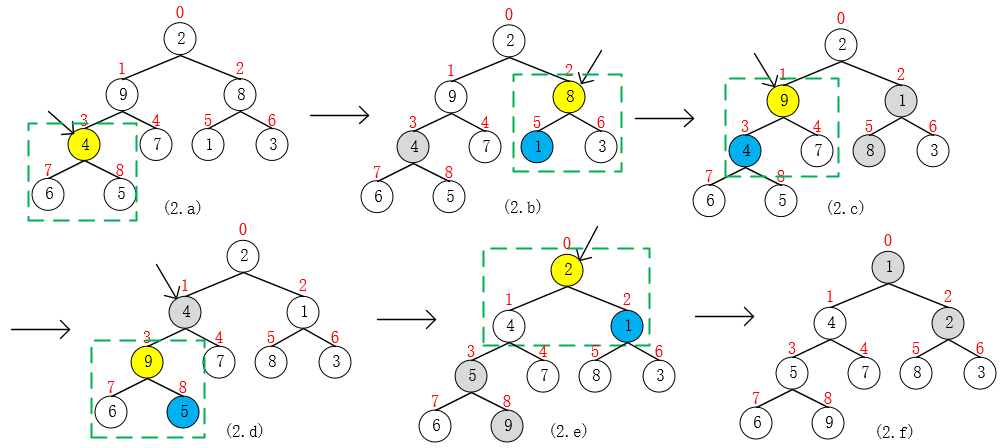
首先，从下到上，从右到左，找到第一个父结点 i，满足规律：i = (size >>> 1) - 1，这里size = 9，i = 3；
比较pq[3, 7, 8]中的元素，将最小的元素pq[x]与堆顶元素pq[3]互换，由于pq[x] = pq[3]，所以无互换；
移动到下一个父结点 i = 2，同理，比较pq[2, 5, 6]中的元素，将最小的元素pq[5]与pq[2]互换，后面的操作同理；
需要注意，当pq[1]（9）和pq[3]（4）互换后（如图2.d），pq[3, 7, 8]违背了最小堆的性质，所以需要进一步调整（向下调整），当调整到叶结点时（i >= size/2）结束；

回到目录

三. 添加元素

添加元素：add(e)，offer(e)，由于添加元素可能破坏堆的性质，所以需要调用siftUp(i, e)向上调整来维护堆性质。同样，siftUp(i, e)根据有无自定义比较器来决定调用siftUpUsingComparator(k, e)还是siftUpComparable(k, e)。在我举的例子中，使用的是siftUpComparable(k, e)。下面是添加元素的相关源码：

 1 public boolean offer(E e) {
 2     if (e == null)
 3         throw new NullPointerException();
 4     modCount++;
 5     int i = size;
 6     if (i >= queue.length)
 7         grow(i + 1);
 8     siftUp(i, e);
 9     size = i + 1;
10     return true;
11 }
12 
13 @SuppressWarnings("unchecked")
14 private void siftUpComparable(int k, E x) {
15     Comparable<? super E> key = (Comparable<? super E>) x;
16     while (k > 0) {
17         int parent = (k - 1) >>> 1;
18         Object e = queue[parent];
19         if (key.compareTo((E) e) >= 0)
20             break;
21         queue[k] = e;
22         k = parent;
23     }
24     queue[k] = key;
25 }

View Code

源码中 grow(i + 1) 是当pq[ ]容量不够时的增长策略，目前可以不用考虑。现在来看往最小堆 pq = {3, 5, 6, 7, 8, 9} 中添加元素 1的过程。算法时间复杂度为O(lgn)，n = size。

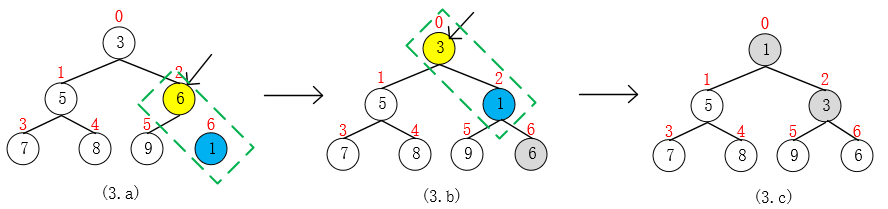
首先，把要添加的元素 1 放到pq[size]，然后调用siftUp(k, e)来维护堆，调整结束后 size++；
向上调整(k, e)时，先找到结点pq[k]的父结点，满足规律 parent = (k - 1) >>> 1，例子中，k = 6, parent = 2；
比较pq[k]与pq[parent]，将较小者放到高处，较大者移到低处，例子中，交换pq[6]（1）与pq[2]（6）的位置；
此次交换结束后，令 k = parent，继续以同样的方法操作，直到 k <= 0 时（到达根结点）结束；

回到目录

四. 索引

indexOf(o)是个私有方法，但好多公开方法中都调用了它，比如：remove(o)，contains(o)等，所以在这里也简单提一下。该算法并不复杂。时间复杂度为O(n)，n = size。

1 private int indexOf(Object o) {
2     if (o != null) {
3         for (int i = 0; i < size; i++)
4             if (o.equals(queue[i]))
5                 return i;
6     }
7     return -1;
8 }

View Code

indexOf(o)中比较两个元素是否相等，使用的是equals()，而接下来要提的removeEq(o)中直接使用了 == 来判断，请读者注意区别。

回到目录

五. 删除元素

remove(o)、removeEq(o)，二者只是在判断两个元素是否相等时使用的方法不同（前者使用equals()，后者使用==），其他内容相同，它们都调用了removeAt(i)来执行删除操作。删除元素后很可能会破坏堆的性质，所以同样需要进行维护。删除元素的维护要比添加元素的维护稍微复杂一点，因为可能同时涉及了：向上调整siftUp和向下调整siftDown。源码如下：

 1 public boolean remove(Object o) {
 2     int i = indexOf(o);
 3     if (i == -1)
 4         return false;
 5     else {
 6         removeAt(i);
 7         return true;
 8     }
 9 }
10 
11 boolean removeEq(Object o) {
12     for (int i = 0; i < size; i++) {
13         if (o == queue[i]) {
14             removeAt(i);
15             return true;
16         }
17     }
18     return false;
19 }
20 
21 @SuppressWarnings("unchecked")
22 E removeAt(int i) {
23     // assert i >= 0 && i < size;
24     modCount++;
25     int s = --size;
26     if (s == i) // removed last element
27         queue[i] = null;
28     else {
29         E moved = (E) queue[s];
30         queue[s] = null;
31         siftDown(i, moved);
32         if (queue[i] == moved) {
33             siftUp(i, moved);
34             if (queue[i] != moved)
35                 return moved;
36         }
37     }
38     return null;
39 }

View Code

我们还是通过例子来学习吧，通过对 pq = {0, 1, 7, 2, 3, 8, 9, 4, 5, 6} 进行一系列删除操作，来理解算法的运作过程。算法时间复杂度O(lgn)，n = size。

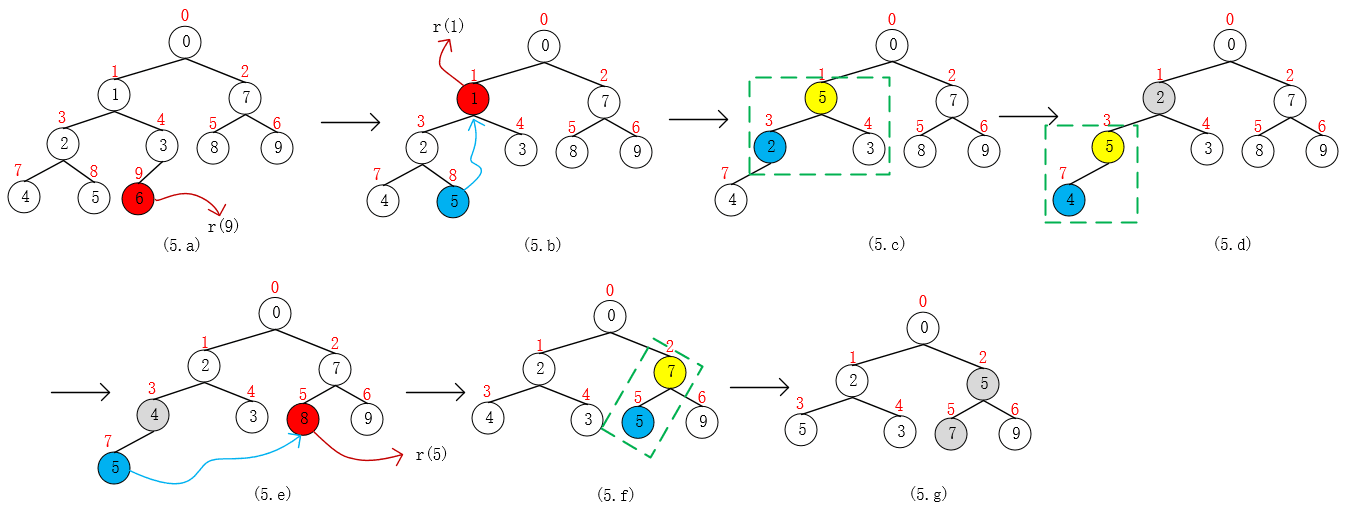
第1步，remove(6)，indexOf(6) = 9，removeAt(9)（用r(9)表示，后面同理）,由于i = 9为队列末端，删除后不会破坏堆性质，所以可以直接删除；
第2步，remove(1)，即r(1)，根据图(5.b)可以看出，算法是拿队列尾部pq[8]去替换pq[1]，替换后破坏了最小堆的性质，需要向下调整进行维护；
第3步，remove(8)，即r(5)，使用队列尾部元素pq[7]替换pq[5]，替换后破坏了最小堆的性质，需要向上调整进行维护；

回到目录

六. 取堆顶

peek()可以在O(1)的时间复杂度下取到堆顶元素pq[0]，看源码一目了然：

1 @SuppressWarnings("unchecked")
2 public E peek() {
3     return (size == 0) ? null : (E) queue[0];
4 }

View Code

回到目录

七. 删除堆顶

删除堆顶使用poll()方法，其算法思想等价于removeAt(0)（时间复杂度O(lgn)），稍微有点区别的是，其只涉及到向下调整，不涉及向上调整。不清楚的朋友可以参看（五. 删除元素），下面是源码：

 1 @SuppressWarnings("unchecked")
 2 public E poll() {
 3     if (size == 0)
 4         return null;
 5     int s = --size;
 6     modCount++;
 7     E result = (E) queue[0];
 8     E x = (E) queue[s];
 9     queue[s] = null;
10     if (s != 0)
11         siftDown(0, x);
12     return result;
13 }

View Code

回到目录

八. 清除队列

清除队列clear()，就是依次把pq[i]置为null，然后size置0，但是pq.length没有改变。时间复杂度为O(n)，n = size。源码如下：

1 public void clear() {
2     modCount++;
3     for (int i = 0; i < size; i++)
4         queue[i] = null;
5     size = 0;
6 }

View Code

回到目录

九. 遍历

可以使用迭代器（Iterator）来遍历pq[ ]本身，或者调用toArray()、toArray(T[] a)方法来生成一个pq[ ]的副本进行遍历。遍历本身的时间复杂度为O(n)，n = size。

使用迭代器遍历 pq = {0, 1, 7, 2, 3, 8, 9, 4, 5, 6}，方法如下：

 1 public static void traverse1(PriorityQueue<Integer> x) {
 2     Iterator<Integer> it = x.iterator();
 3     while (it.hasNext()) {
 4         System.out.print(it.next() + " ");
 5     }
 6     System.out.println();
 7 }
 8 // 或者更简单的，结合java语法糖，可以写成如下形式
 9 public static void traverse2(PriorityQueue<Integer> x) {
10     for (int a : x) {
11         System.out.print(a + " ");
12     }
13     System.out.println();
14 }
15 /* 输出
16 0 1 7 2 3 8 9 4 5 6 
17 */

View Code

通过拷贝pq[ ]副本来遍历，方法如下：

 1 public static void traverse3(PriorityQueue<Integer> x) {
 2     Object[] ins = x.toArray();
 3     for (Object a : ins) {
 4         System.out.print((Integer)a + " ");
 5     }
 6     System.out.println();
 7 }
 8 
 9 public static void traverse4(PriorityQueue<Integer> x) {
10     Integer[] ins = new Integer[100];
11     ins = x.toArray(ins);
12     for (int i = 0, len = x.size(); i < len; i++) {
13         System.out.print(ins[i] + " ");
14     }
15     System.out.println();
16 }
17 /* 输出
18 0 1 7 2 3 8 9 4 5 6 
19 */

View Code

在使用toArray(T[] a)拷贝来进行遍历时，需要注意（x表示PriorityQueue对象）：

如果ins[ ]的容量大于x.size()，请使用for (int i = 0; i < x.size(); i++) 来遍历，否则可能会获取到多余的数据；或者你使用for (int a : ins)来遍历时，可能导致NullPointerException异常；
请使用 ins = x.toArray(ins) 的写法来确保正确获取到pq[ ]副本。当ins[ ]容量大于x.size()时，写为 x.toArray(ins) 能正确获取到副本，但当ins[ ]容量小于x.size()时，该写法就无法正确获取副本。因为此情况下toArray(T[] a)内部会重新生成一个大小为x.size()的Integer数组进行拷贝，然后return该数组；

toArray(T[] a)源码如下：

 1 @SuppressWarnings("unchecked")
 2 public <T> T[] toArray(T[] a) {
 3     final int size = this.size;
 4     if (a.length < size)
 5         // Make a new array of a''s runtime type, but my contents:
 6         return (T[]) Arrays.copyOf(queue, size, a.getClass());
 7     System.arraycopy(queue, 0, a, 0, size);
 8     if (a.length > size)
 9         a[size] = null;
10     return a;
11 }

View Code

回到目录

十. 小测试

下面来说说文章开头我提到的那个题目吧，如下（点击这里在线做题）（请使用PriorityQueue来完成）：

/* 数据流中的中位数
题目描述
如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。
如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，
使用GetMedian()方法获取当前读取数据的中位数。
*/

public class Solution {
    public void Insert(Integer num) {}
    public Double GetMedian() {}
}

我写的参考代码（带解析），如下：

 1 /*
 2 关键点：
 3  大根堆maxq       小根堆minq
 4 ----------      -------------
 5           \    /
 6   <= A     A  B   >= B
 7           /    \
 8 ----------      -------------
 9  
10 每次insert(num)前要确保 ：
11     1) maxq.size == q.size // 偶数个时，二者元素个数相等
12 或  2) minq.size == maxq.size + 1 // 奇数个时把多余的1个放到小根堆minq
13 这样一来，获取中位数时：
14 奇数个：minq.top;
15 偶数个：(minq.top + maxq.top) / 2
16  
17 每次isnert(num)后，可能会打破上面的条件，出现下面的情况：
18     1) maxq.size == q.size + 1 // 打破条件(1) => 这时需要把maxq.top放到minq中
19 或  2) minq.size == maxq.size + 2 // 打破条件(2) => 这时需要把minq.top放到maxq中
20 */
21 
22 import java.util.Comparator;
23 import java.util.PriorityQueue;
24  
25 public class JZOffer_63_Solution_02 {
26     PriorityQueue<Integer> minq = new PriorityQueue<Integer>();
27     PriorityQueue<Integer> maxq = new PriorityQueue<Integer>((o1, o2) -> o2.compareTo(o1));
28 
29     public void Insert(Integer num) {
30         if (minq.isEmpty() || num >= minq.peek()) minq.offer(num);
31         else maxq.offer(num);
32         if (minq.size() == maxq.size()+2) maxq.offer(minq.poll());
33         if (maxq.size() == minq.size()+1) minq.offer(maxq.poll());
34     }
35 
36     public Double GetMedian() {
37         return minq.size() == maxq.size() ? (double)(minq.peek()+maxq.peek())/2.0 : (double)minq.peek();
38     }
39 }

View Code

回到目录

转载请说明出处，have a good time! :D

Java Collection - PriorityQueue 优先队列

总结

优先队列的作用是能保证每次取出的元素都是队列中权值最小的（Java的优先队列每次取最小元素，C++的优先队列每次取最大元素）。这里牵涉到了大小关系，元素大小的评判可以通过元素本身的自然顺序（natural ordering），也可以通过构造时传入的比较器（Comparator，类似于C++的仿函数）。
Java中PriorityQueue实现了Queue接口，不允许放入null元素；其通过堆实现，具体说是通过完全二叉树（complete binary tree）实现的小顶堆（任意一个非叶子节点的权值，都不大于其左右子节点的权值）。
Java中使用数组的形式保存小顶堆的结构。父节点和子节点的编号是有联系的，更确切的说父子节点的编号之间有如下关系：

leftNo = parentNo*2+1

rightNo = parentNo*2+2

parentNo = (nodeNo-1)/2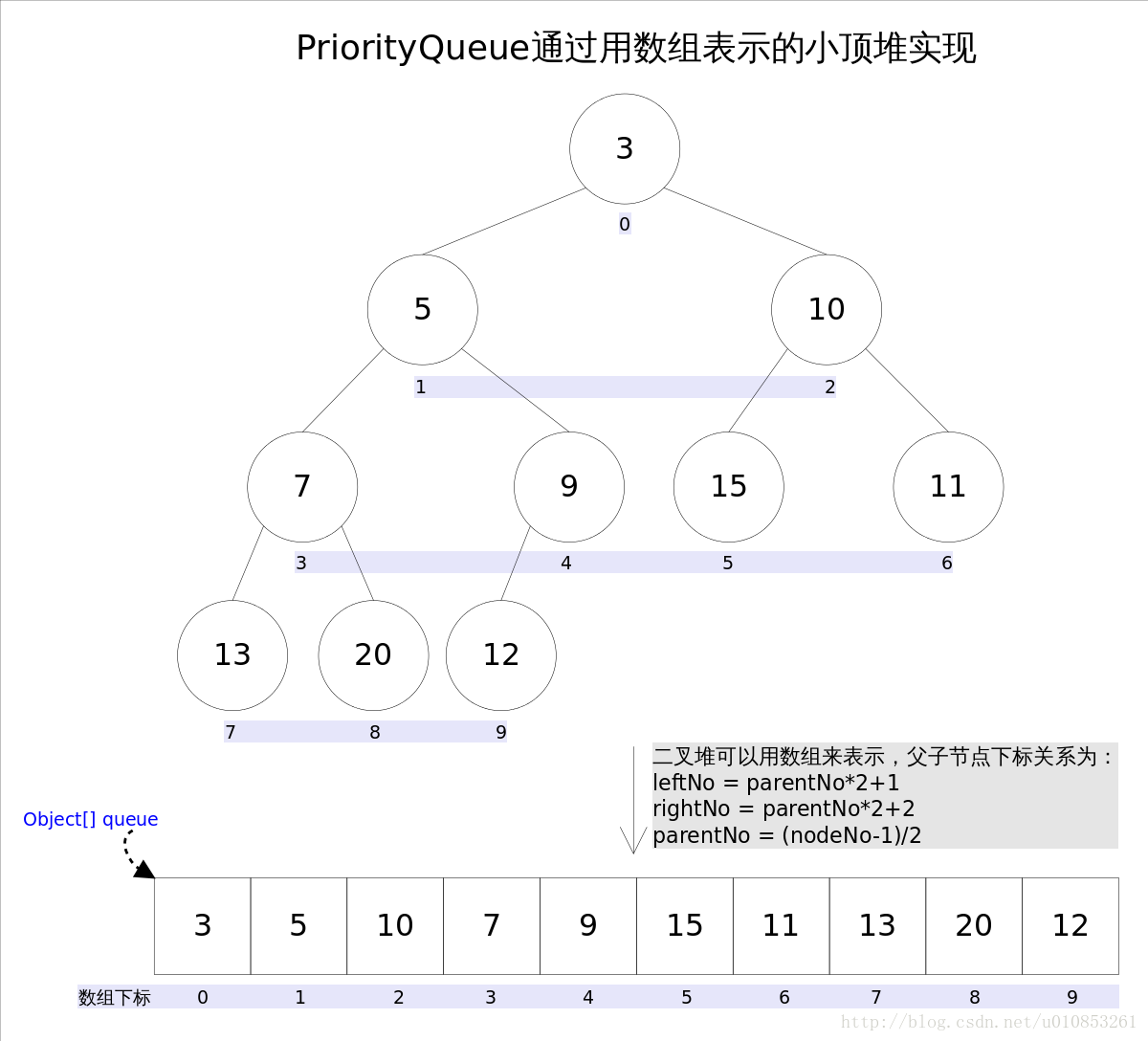

PriorityQueue解析

详细内容

PriorityQueue 继承关系
add() & offer() 源码 -- add(E e)和offer(E e)的语义相同，都是向优先队列中插入元素，只是Queue接口规定二者对插入失败时的处理不同，前者在插入失败时抛出异常，后则则会返回false。对于PriorityQueue这两个方法其实没什么差别。
peek() 源码
remove() & poll() 源码 -- remove()和poll()方法的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回null。由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。

参考链接

PriorityQueue 原理与应用
深入理解Java PriorityQueue

PriorityQueue 时间复杂度

Binary heap （二叉树堆）, Java默认使用, 也就是第一行。
Fibonacci heap （斐波那契堆），Strict Fibonacci（严格斐波那契堆）理论性能最好 --> 记住大体概念，结论即可。
Binomial heap（二项堆）

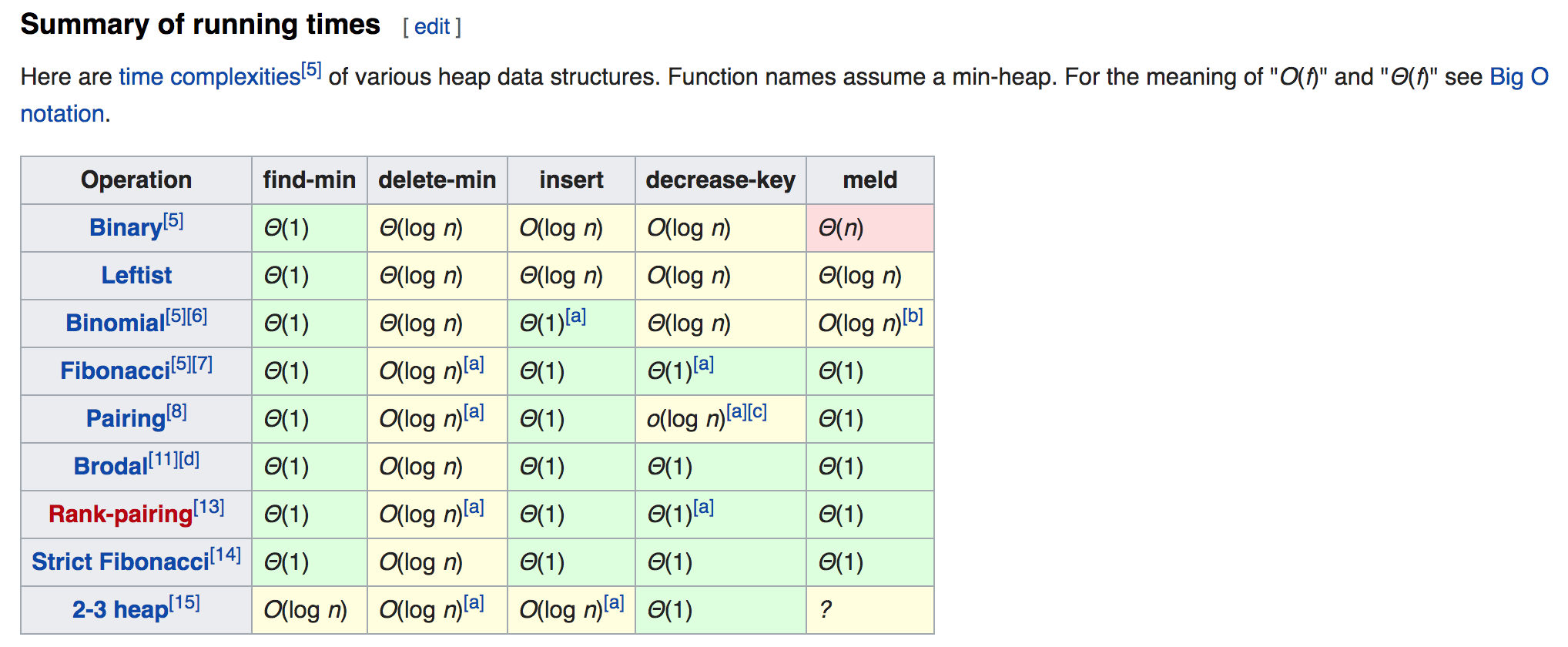
Fibonacci heap （斐波那契堆）的优缺点

Fibonacci heap （斐波那契堆）的优点:

斐波那契堆的结构较二项堆更松散。因此对结构的维护可以到方便时再做。

1.二叉堆及二项堆在插入一个结点后,会马上维护堆的结构...而FIB堆却将这个工作延迟到FIB_EXTRACT_MIN的时候再做....使元素的插入的时间为O(1)
2.二叉堆及二项堆在改变一个结点的值的时候,会马上维护堆的结构...而FIB堆却将这个工作延迟到FIB_EXTRACT_MIN的时候再做....使元素的值的改变的时间为O(1)
3.堆的合并..FIB堆只需要将两个堆的根表合并就可以了 O(1)

Fibonacci heap （斐波那契堆）的难点:

FIB_EXTRACT_MIN()...提取最小的值。

1.将min结点的儿子都加入到根表
2.在根表中除去min结点
3.合并堆的根表,即减少根表中堆的数目,直到根表中每个根的度都不相同(用merge()函数)

今天的关于PriorityQueue：无法将学生转换为java.lang.Comparable和无法将javac项识别为怎么改的分享已经结束，谢谢您的关注，如果想了解更多关于# Java Queue系列之PriorityQueue、c – 无法将派生的Compare传递给std :: priority_queue、Java - PriorityQueue、Java Collection - PriorityQueue 优先队列的相关知识，请在本站进行查询。

本文标签：