最近很多小伙伴都在问莫烦python教程学习笔记——learn_curve曲线用于过拟合问题和曲线拟合python这两个问题,那么本篇文章就来给大家详细解答一下,同时本文还将给你拓展LearningC
最近很多小伙伴都在问莫烦python教程学习笔记——learn_curve曲线用于过拟合问题和曲线拟合 python这两个问题,那么本篇文章就来给大家详细解答一下,同时本文还将给你拓展Learning Curve 与 偏差方差 (判断欠过拟合)、Python 学习之《Learn Python3 The Hard Way 》第三部分学习笔记、Python 学习笔记之——用 sklearn 对数据进行预处理、python2.7学习笔记——菜鸟教程等相关知识,下面开始了哦!
本文目录一览:- 莫烦python教程学习笔记——learn_curve曲线用于过拟合问题(曲线拟合 python)
- Learning Curve 与 偏差方差 (判断欠过拟合)
- Python 学习之《Learn Python3 The Hard Way 》第三部分学习笔记
- Python 学习笔记之——用 sklearn 对数据进行预处理
- python2.7学习笔记——菜鸟教程

莫烦python教程学习笔记——learn_curve曲线用于过拟合问题(曲线拟合 python)
# View more python learning tutorial on my Youtube and Youku channel!!!
# Youtube video tutorial: https://www.youtube.com/channel/UCdyjiB5H8Pu7aDTNVXTTpcg
# Youku video tutorial: http://i.youku.com/pythontutorial
"""
Please note, this code is only for python 3+. If you are using python 2+, please modify the code accordingly.
"""
from __future__ import print_function
from sklearn.learning_curve import learning_curve
from sklearn.datasets import load_digits
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
digits = load_digits()
X = digits.data
y = digits.target
train_sizes, train_loss, test_loss= learning_curve(
SVC(gamma=0.01), X, y, cv=10, scoring=''mean_squared_error'',
train_sizes=[0.1, 0.25, 0.5, 0.75, 1])
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)
plt.plot(train_sizes, train_loss_mean, ''o-'', color="r",
label="Training")
plt.plot(train_sizes, test_loss_mean, ''o-'', color="g",
label="Cross-validation")
plt.xlabel("Training examples")
plt.ylabel("Loss")
plt.legend(loc="best")
plt.show()

Learning Curve 与 偏差方差 (判断欠过拟合)
之前有一篇文章介绍了什么是偏差(bias)与方差(variance),这篇文章介绍一下如何使用学习曲线来判断模型是否处于欠拟合或过拟合。
什么是学习曲线?
学习曲线就是通过画出不同训练集大小时训练集和验证集的准确率,可以看到模型在新数据上的表现,进而来判断模型是否方差偏高或偏差过高,是否可以通过增加数据集来减少过拟合、是否可以通过增加特征、减少正则项来降低偏差。
怎么解读?
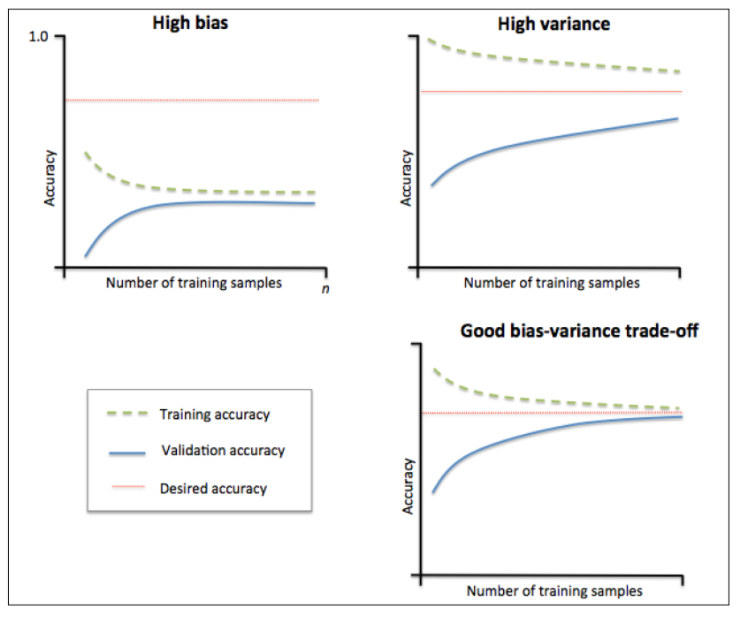
当训练集和测试集的误差收敛但却很高时,为高偏差。
例如左上,偏差很高,训练集和验证集的准确率都很低,很可能是欠拟合。
我们可以增加模型参数,比如,构建更多的特征,减少正则项。
此时通过增加数据量是不起作用的。
当训练集和测试集的误差之间有大的差距时,为高方差。
当训练集的准确率比其他独立数据集上的测试结果的准确率要高时,一般都是过拟合。
例如右上,方差很高,训练集和验证集的准确率相差太多,应该是过拟合。
我们可以增大数据集,降低模型复杂度,增大正则项,或者通过特征选择减少特征数。
理想情况是找到偏差和方差都很小的情况,即收敛且误差较小。
怎么画?
在画学习曲线时,横轴为训练样本的数量,纵轴为准确率。
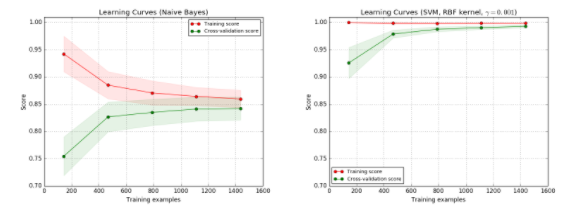
左图为 朴素贝叶斯(Native Bayes)分类器,分数大概收敛在0.85,此时增加数据集对提升结果没有帮助。
右图为 支持向量机(SVM RBF-kernel),训练集的准确率很高,验证集的准确率也随着数据量增加而增加,不过因为训练集还是高于验证集的,处于过拟合状态,所以增加数据集还是对提升结果有帮助的。
代码实现
模型选择GaussianNB和SVC作比较;
模型选择方法中需要用到learning_curve和交叉验证中的ShuffleSplit
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit定义画出学习曲线的方法,
核心是调用了sklearn.model_selection的learning_curve,
学习曲线返回的是train_sizes,train_scores,test_scores,
画训练集的曲线时,横轴是train_sizes,纵轴为train_scores_mean,
画测试集的曲线时,横轴是train_sizes,纵轴为test_scores_mean。
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
~~~
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
~~~在调用plot_learning_curve时,首先定义交叉验证cv和学习模型estimator。
这里交叉验证用的是ShuffleSplit,它首先将样例打散,并随机选取20%的数据集作为测试集,这样选出100次,最后返回的是train_index,test_index,就知道哪些数据是训练集,哪些是测试集。
当estimator是GaussianNB,对应左图:
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)当estimator是SVC时,对应右图:
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)

Python 学习之《Learn Python3 The Hard Way 》第三部分学习笔记
文章目录
- Python 学习之《Learn Python3 The Hard Way 》第三部分学习笔记
-
-
-
- 1、读取文件内容
- 2、对文件进行操作
- 3、把文件 A 的内容写入到 B 文件
-
-
Python 学习之《Learn python3 The Hard Way 》第三部分学习笔记
1、读取文件内容
import sys
if __name__ == '__main__':
if len(sys.argv) 
Python 学习笔记之——用 sklearn 对数据进行预处理
1. 标准化
标准化是为了让数据服从一个零均值和单位方差的标准正态分布。也即针对一个均值为 $mean$ 标准差为 $std$ 的向量 $X$ 中的每个值 $x$,有 $x_{scaled} = \frac{x - mean}{std}$。
>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
>>> X_scaled = preprocessing.scale(X_train)
>>> X_scaled
array([[ 0. ..., -1.22..., 1.33...],
[ 1.22..., 0. ..., -0.26...],
[-1.22..., 1.22..., -1.06...]])
>>> X_scaled.mean(axis=0)
array([0., 0., 0.])
>>> X_scaled.std(axis=0)
array([1., 1., 1.])默认针对每列来进行标准化,也即针对每个特征进行标准化。可以通过设置 axis=1 来对每行进行标准化,也即对每个样本进行标准化。sklearn.preprocessing.scale()
此外,我们还可以用训练数据的均值和方差来对测试数据进行相同的标准化处理。sklearn.preprocessing.StandardScaler()
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> scaler
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> scaler.mean_
array([1. ..., 0. ..., 0.33...])
>>> scaler.scale_
array([0.81..., 0.81..., 1.24...])
>>> scaler.transform(X_train)
array([[ 0. ..., -1.22..., 1.33...],
[ 1.22..., 0. ..., -0.26...],
[-1.22..., 1.22..., -1.06...]])
>>> X_test = [[-1., 1., 0.]] # 用同样的均值和方差来对测试数据进行标准化
>>> scaler.transform(X_test)
array([[-2.44..., 1.22..., -0.26...]])2. 将数据缩放到一定范围
有时候,我们需要数据处在给定的最大值和最小值范围之间,常常是 0 到 1 之间,这样数据的最大绝对值就被限制在了单位大小以内。
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[0.5 , 0. , 1. ],
[1. , 0.5 , 0.33333333],
[0. , 1. , 0. ]])
>>> X_test = np.array([[-3., -1., 4.]]) # 将同样的变换应用到测试数据上
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5 , 0. , 1.66666667]])当 MinMaxScaler() 传入一个参数 feature_range=(min, max),我们可以将数据缩放到我们想要的范围内。sklearn.preprocessing.MinMaxScaler()
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min此外,我们还可以将数据限制在 [-1, 1] 之间,通过除以每个特征的最大绝对值。sklearn.preprocessing.MaxAbsScaler()
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
...
>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. , 1. ],
[ 1. , 0. , 0. ],
[ 0. , 1. , -0.5]])
>>> X_test = np.array([[ -3., -1., 4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. , 2. ]])
>>> max_abs_scaler.scale_
array([2., 1., 2.])3. 归一化
归一化的目的是让每个样本具有单位范数。也即针对向量 $X$ 中的每个值 $x$,有 $x_{normalized} = \frac{x}{||X||}$。
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> X_normalized = preprocessing.normalize(X, norm=''l2'')
>>> X_normalized
array([[ 0.40..., -0.40..., 0.81...],
[ 1. ..., 0. ..., 0. ...],
[ 0. ..., 0.70..., -0.70...]])
>>> normalizer = preprocessing.Normalizer().fit(X) # fit does nothing
>>> normalizer
Normalizer(copy=True, norm=''l2'')
>>> normalizer.transform(X)
array([[ 0.40..., -0.40..., 0.81...],
[ 1. ..., 0. ..., 0. ...],
[ 0. ..., 0.70..., -0.70...]])
>>> normalizer.transform([[-1., 1., 0.]])
array([[-0.70..., 0.70..., 0. ...]])默认是对每行数据用 $L2$ 范数进行归一化,我们也可以选择 $L1$ 范数或者针对每列进行归一化。sklearn.preprocessing.Normalizer()
获取更多精彩,请关注「seniusen」!

python2.7学习笔记——菜鸟教程
标准数据类型
- Numbers(数字)
- String(字符串)
- List(列表)
- Tuple(元组)
- Dictionary(字典)
list = [ ''runoob'', 786 , 2.23, ''john'', 70.2 ]
tuple = ( ''runoob'', 786 , 2.23, ''john'', 70.2 )
元组用 () 标识。内部元素用逗号隔开。但是元组不能二次赋值,相当于只读列表。
if,elfi,else等后面写“冒号”
def sample(n_samples): pass该处的 pass 便是占据一个位置,因为如果定义一个空函数程序会报错,当你没有想好函数的内容是可以用 pass 填充,使程序可以正常运行。
list.append(''Google'') ## 使用 append() 添加元素
dict = {''Name'': ''Zara'', ''Age'': 7, ''Class'': ''First''}
print "dict[''Name'']: ", dict[''Name'']
print "dict[''Age'']: ", dict[''Age'']
函数代码块以 def 关键词开头,后接函数标识符名称和圆括号()。
def functionname( parameters ):
"函数_文档字符串"
function_suite
return [expression]
全局变量和局部变量
定义在函数内部的变量拥有一个局部作用域,定义在函数外的拥有全局作用域。
局部变量只能在其被声明的函数内部访问,而全局变量可以在整个程序范围内访问。调用函数时,所有在函数内声明的变量名称都将被加入到作用域中。
搜索路径
当你导入一个模块,Python 解析器对模块位置的搜索顺序是:
- 1、当前目录
- 2、如果不在当前目录,Python 则搜索在 shell 变量 PYTHONPATH 下的每个目录。
- 3、如果都找不到,Python会察看默认路径。UNIX下,默认路径一般为/usr/local/lib/python/。
模块搜索路径存储在 system 模块的 sys.path 变量中。变量里包含当前目录,PYTHONPATH和由安装过程决定的默认目录。
globals() 和 locals() 函数
根据调用地方的不同,globals() 和 locals() 函数可被用来返回全局和局部命名空间里的名字。
如果在函数内部调用 locals(),返回的是所有能在该函数里访问的命名。
如果在函数内部调用 globals(),返回的是所有在该函数里能访问的全局名字。
两个函数的返回类型都是字典。所以名字们能用 keys() 函数摘取。
关于莫烦python教程学习笔记——learn_curve曲线用于过拟合问题和曲线拟合 python的问题就给大家分享到这里,感谢你花时间阅读本站内容,更多关于Learning Curve 与 偏差方差 (判断欠过拟合)、Python 学习之《Learn Python3 The Hard Way 》第三部分学习笔记、Python 学习笔记之——用 sklearn 对数据进行预处理、python2.7学习笔记——菜鸟教程等相关知识的信息别忘了在本站进行查找喔。
本文标签:






