GVKun编程网logo

ZOJ Monthly, January 2019 I Little Sub and Isomorphism Sequences(set 妙用) ZOJ4089

9

对于ZOJMonthly,January2019ILittleSubandIsomorphismSequences(set妙用)ZOJ4089感兴趣的读者，本文将提供您所需要的所有信息，并且为您提供关

对于ZOJ Monthly, January 2019 I Little Sub and Isomorphism Sequences(set 妙用) ZOJ4089感兴趣的读者，本文将提供您所需要的所有信息，并且为您提供关于2018ICPC青岛区域赛 zoj4062 Plants vs. Zombies、2019山东ACM省赛K题 zoj4123 Happy Equation、Atlassian - Confluence Security Advisory - 2019-03-20、BZOJ 5381 or & Codeforces 623E Transforming Sequence DP+NTT的宝贵知识。

本文目录一览：

ZOJ Monthly, January 2019 I Little Sub and Isomorphism Sequences(set 妙用) ZOJ4089

ZOJ Monthly, January 2019 I Little Sub and Isomorphism Sequences(set 妙用) ZOJ4089

写这篇博客来证明自己的愚蠢 。。。Orz 

飞机

题意：给定你个数组，以及一些单点修改，以及询问，每次询问需要求得，最长的字串长度，它在其他位置存在同构

 

题解：经过一些奇思妙想后 ，你可以发现问题是传化为了查询一个最大的区间这个区间的开头和结尾是相同的 ； 

所以如果我们知道了某个数的最小位置与最大位置 ， 我们是不是就可以很快的知道这个答案了 ， 那问题又会来了 ， 我怎样得到这个最早和最晚呢 ？ 这里相当的疯狂 ， 开了20W的set , 没错就是set , 其本身也是排了序的 ， 所以我们将某数的所有的位置都放入到对应的set ， 我们是不是就可以很快的查找与删除了；

但是题目给出的数据有10^9 , 我们是不是需要离散化 ， 可是又带有修改 ， 那我们是不是参考离线的打法 ， 先将所以需要用的的数字存下来 ， 离散化呀 ；

 

那问题又来拉 ， 我怎么可以很快的得到最大的区间 ， 我看到网上是有用线段树的Orz ， 我是不会拉 ， 所以我用了set..  没有看错 ，就是set  , 不过这个set 是一个结构体set ，里面记录的是某个数与这个数字对应的区间长度 ， 为什么没有想到优先队列呢 ， 很显然修改是会改变对应数的对应区间最大值 ，所以我们得用利于修改的数据结构 ，于是。。。。这题就set。。。

 

然后！！！我DUG了一晚 ， 原来set 的删除并不是单纯的删除某数 ， 比如你要删除X ， 你要这样打 ，G.erase(G.find(X)); 卧槽。。我直接G..erase(X)  被自己蠢哭。。。还要注意删除前要判断容器里面是否有这样数，没有就不可以删除，这些是血的教训，希望我以后可以记得。Orz

 

 

#include<bits/stdc++.h>
using namespace std ;
#define N 200001

set<int> ST[N];
int a[N],b[N],n,m;
int Len;
struct no
{
    int op , x, y;
}q[N];

struct NO
{
    int id;
    int val;
    bool operator < (const NO &a) const
    {
        return a.val<val;
    }
}M,MM;
multiset<NO>G;
multiset<NO>::iterator it;
void Hash()
{
    sort(b+1,b+1+Len);
    Len=unique(b+1,b+1+Len)-b-1;

    for(int i=1 ; i<=n ; i++)
    a[i]=lower_bound(b+1,b+1+Len,a[i])-b;

    for(int i=1 ; i<=m ; i++)
    {
        if(q[i].op==1)
        {
            q[i].y=lower_bound(b+1,b+1+Len,q[i].y)-b;
        }
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(int i=1 ; i<=n+m ; i++ )
        ST[i].clear();
        Len=0;G.clear();
        memset(q,0,sizeof(q));
        for(int i=1 ; i<=n ; i++)
        {
            scanf("%d",&a[i]);
            b[++Len]=a[i];///离散化
        }
        for(int i=1 ; i<=m ; i++)
        {
            int op,x,y;
            scanf("%d",&op);
            if(op==1)
            {
                scanf("%d%d",&x,&y);
                q[i].op=op ; q[i].x=x ; q[i].y=y;
                b[++Len]=y;
            }
        }
        Hash();
        for(int i=1 ; i<=n ; i++)
        ST[a[i]].insert(i);

        for(int i=1 ; i<=n+m ; i++)
        {
            if(ST[i].size()>=2)
            {
                 M.id=i; M.val=(*ST[i].rbegin())-(*ST[i].begin());
                 G.insert(M);
            }
        }


        for(int i=1 ; i<=m ; i++)
        {
            if(q[i].op==1)
            {

                int v = a[q[i].x] , X=q[i].x , Y=q[i].y;
                int LEN=(*ST[v].rbegin())-(*ST[v].begin());
                M.id=v; M.val=LEN;
                if(ST[v].find(X)!=ST[v].end())
                ST[v].erase(ST[v].find(X));

                 if(G.find(M)!=G.end())
                G.erase(G.find(M));


                if(ST[v].size()>=2)
                {
                M.val=(*ST[v].rbegin())-(*ST[v].begin());
                G.insert(M);
                }
                a[X]=Y;
                v=Y;
                if(ST[v].size()>=2)
                {
                    M.id=v;
                    M.val=(*ST[v].rbegin())-(*ST[v].begin());
                    G.erase(G.find(M));
                }
                ST[v].insert(X);
                if(ST[v].size()>=2)
                {
                M.id=v ; M.val=(*ST[v].rbegin())-(*ST[v].begin());
                G.insert(M);
                }
            }
            else
            {

                if(G.empty())
                puts("-1");
                else
                {
                    M=(*G.begin());
                    if((M.val)==0)
                    puts("-1");
                    else
                    printf("%d\n",(M.val));
                }

            }
           /* printf("%d\n",i);
            for(it=G.begin() ; it!=G.end() ; it++)
            {
                MM=*it;
                printf("%d %d\n",MM.id,MM.val);
            }*/

        }


    }
        return 0;
}
View Code

 

2018ICPC青岛区域赛 zoj4062 Plants vs. Zombies

2018ICPC青岛区域赛 zoj4062 Plants vs. Zombies

　　BaoBao and DreamGrid are playing the game Plants vs. Zombies. In the game, DreamGrid grows plants to defend his garden against BaoBao''s zombies.


Plants vs. Zombies(?)
(Image from pixiv. ID: 21790160; Artist: socha)

There are  plants in DreamGrid''s garden arranged in a line. From west to east, the plants are numbered from 1 to  and the -th plant lies  meters to the east of DreamGrid''s house. The -th plant has a defense value of  and a growth speed of . Initially,  for all .

DreamGrid uses a robot to water the plants. The robot is in his house initially. In one step of watering, DreamGrid will choose a direction (east or west) and the robot moves exactly 1 meter along the direction. After moving, if the -th plant is at the robot''s position, the robot will water the plant and  will be added to . Because the water in the robot is limited, at most  steps can be done.

The defense value of the garden is defined as . DreamGrid needs your help to maximize the garden''s defense value and win the game.

Please note that:

  • Each time the robot MUST move before watering a plant;
  • It''s OK for the robot to move more than  meters to the east away from the house, or move back into the house, or even move to the west of the house.

Input

There are multiple test cases. The first line of the input contains an integer , indicating the number of test cases. For each test case:

The first line contains two integers  and  (, ), indicating the number of plants and the maximum number of steps the robot can take.

The second line contains  integers  (), where  indicates the growth speed of the -th plant.

It''s guaranteed that the sum of  in all test cases will not exceed .

Output

For each test case output one line containing one integer, indicating the maximum defense value of the garden DreamGrid can get.

Sample Input

2
4 8
3 2 6 6
3 9
10 10 1

Sample Output

6
4

Hint

In the explanation below, ''E'' indicates that the robot moves exactly 1 meter to the east from his current position, and ''W'' indicates that the robot moves exactly 1 meter to the west from his current position.

For the first test case, a candidate direction sequence is {E, E, W, E, E, W, E, E}, so that we have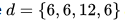  after the watering.

For the second test case, a candidate direction sequence is {E, E, E, E, W, E, W, E, W}, so that we haveafter the watering.

 

 

#include "bits/stdc++.h"

using namespace std;
typedef long long ll;
const int maxn = 1e5 + 100;
ll n, m;
ll a[maxn];
ll b[maxn];

bool check(ll minn) {
    for (int i = 0; i < n; i++) {
        b[i] = (minn + a[i] - 1ll) / a[i];
    }
    ll sum = 0ll;
    for (int i = 0; i < n; i++) {
        if (b[i] == 0ll) {
            if (i != n - 1ll) sum++;
        } else {
            sum += b[i] * 2ll - 1ll;
            b[i + 1] = b[i + 1] - b[i] + 1ll;
            if (b[i + 1] < 0) b[i + 1] = 0;
        }
        if (sum > m) return 0;
    }
    return sum <= m;
}

int main() {
    //freopen("input.txt", "r", stdin);
    int _;
    cin >> _;
    while (_--) {
        cin >> n >> m;
        for (int i = 0; i < n; i++) {
            cin >> a[i];
        }
        ll l = 0, r = 100005 * m;
        ll mid;
        while (l < r) {
            mid = (l + r + 1) / 2;
            if (check(mid)) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        cout << l << endl;
    }
    return 0;
}

 

2019山东ACM省赛K题 zoj4123 Happy Equation

2019山东ACM省赛K题 zoj4123 Happy Equation

<center> Happy Equation </center>

<center>Time Limit: 1 Second Memory Limit: 65536 KB</center>

Little Sub has just received an equation, which is shown below, as his birthday gift. $ a^x \equiv x^a (\text{mod } 2^p) $ Given the value of , please help Little Sub count the number of x($ 1 \le x \le 2^p $ )which satisfies the equation.

Input

There are multiple test cases. The first line of the input contains an integer T (about 1000), indicating the number of test cases. For each test case:

The first and only line contains two integers and p ($1 \leq a \leq 10^9$,$1 \leq p \leq 30$ ).

Output

For each test case output one line containing one integer, indicating the answer.

Sample Input

2 6 12 8 16

Sample Output

1023 16383

比赛的时候想到了会和二进制有关系，但是没想出来具体的关系……

打表易知当a为奇数是答案为1（目前还不知道怎么证明）.

将$a$分解为$2^{k_1}+2^{k_2}+…+2^{k_n}(k_1<k_2<…<k_n)$,则$a^x = {(2^{k_1}+2^{k_2}+…+2^{k_n})}^x$,显然只要${(2^{k_1})}^x \text{mod } 2^p = 0$ ，则$a^x \text{mod } 2^p = 0$.即只要$k_1 *x >=p $ ,就有$a^x \text{mod } 2^p = 0$。这就需要另$x^a \text{mod}2^p=0$ ,设x的最低位1为第$k_x$位，则需要满足$k_x *a>=p$ ，可以求出$k_x$ ，所有 $x^a \equiv 0 (\text{mod } 2^p)$的x为公差为$2^{k_x}$ 的等差数列。

然后再特判一下x较小时的情况就可以了。

#include "bits/stdc++.h"

using namespace std;

typedef long long ll;
ll mod;

ll powmod(ll a, ll b) {
    ll ret = 1;
    while (b) {
        if (b & 1) ret = ret * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return ret;
}

int main() {
    //freopen("in.txt", "r", stdin);
    ll a, p;
    int _;
    cin >> _;
    while (_--) {
        cin >> a >> p;
        mod = pow(2, p);
        if (a % 2) {
            cout << 1 << endl;
            continue;
        }
        ll ans = 0;
        ll ka, xl;
        for (int i = 1; i <= 33; i++) {
            if (a & (1ll << i)) {
                ka = i;
                break;
            }
        }
        xl = (p + ka - 1) / ka;
        ll kx = (p + a - 1) / a;
        kx = pow(2, kx);
        ans = (pow(2, p) - max(xl, kx)) / kx + 1;
        for (ll i = 1; i <= p; i++) {
            if (powmod(a, i) == powmod(i, a) && powmod(a, i) != 0) ans++;
        }
        cout << ans << endl;
    }
    return 0;
}

Atlassian - Confluence Security Advisory - 2019-03-20

Atlassian - Confluence Security Advisory - 2019-03-20

 https://www.cnblogs.com/iAmSoScArEd/

--------------------

This problem refers to the advisory found at https://confluence.atlassian.com/display/DOC/Confluence+Security+Advisory+-+2019-03-20


CVE ID:

* CVE-2019-3395.

* CVE-2019-3396.


Product:

Confluence Server and Confluence Data Center.

 

Affected Confluence Server and Confluence Data Center product versions:

6.6.0 <= version < 6.6.12

6.12.0 <= version < 6.12.3
6.13.0 <= version < 6.13.3
6.14.0 <= version < 6.14.2


Fixed Confluence Server and Confluence Data Center product versions:

* for 6.6.x, Confluence Server and Data Center 6.6.12 have been released with a fix for these issues.

* for 6.12.x, Confluence Server and Data Center 6.12.3 have been released with a fix for these issues.

* for 6.13.x, Confluence Server and Data Center 6.13.3 have been released with a fix for these issues.

* for 6.14.x, Confluence Server and Data Center 6.14.2 have been released with a fix for these issues.



Summary:

 

This advisory discloses critical severity security vulnerabilities. Versions of Confluence Server and Data Center before 6.6.12 (the fixed version for 6.6.x),  from version 6.7.0 before 6.12.3 (the fixed version for 6.12.x), from version 6.13.0 before 6.13.3 (the fixed version for 6.13.x) and from version 6.14.0 before 6.14.2 (the fixed version for 6.14.x) are affected by these vulnerabilities.


Customers who have upgraded Confluence to version 6.6.12 or 6.12.3 or 6.13.3 or 6.14.2 are not affected.


Customers who have downloaded and installed Confluence >= 6.6.0 but less than 6.6.12 (the fixed version for 6.6.x) or who have downloaded and installed Confluence >= 6.12.0 but less than 6.12.3(the fixed version for 6.12.x) or who have downloaded and installed Confluence >= 6.13.0 but less than 6.13.3 (the fixed version for 6.13.x) or who have downloaded and installed Confluence >=  6.14.0 but less than 6.14.2 (the fixed version for 6.14.x) please upgrade your Confluence installations immediately to fix these vulnerabilities.

 


WebDAV vulnerability (CVE-2019-3395)
Severity:
Atlassian rates the severity level of this vulnerability as critical, according to the scale published in our Atlassian severity levels. The scale allows us to rank the severity as critical, high, moderate or low. This is our assessment and you should evaluate its applicability to your own IT environment.

 

Description:
A remote attacker is able to exploit a Server-Side Request Forgery (SSRF) vulnerability via the WebDAV plugin to send arbitrary HTTP and WebDAV requests from a Confluence Server or Data Center instance. Versions of Confluence before version 6.6.7 (the fixed version for 6.6.x), from version 6.7.0 before 6.7.3 (the fixed version for 6.7.x), from version 6.8.0 before 6.8.5 (the fixed version for 6.8.x) and from version 6.9.0 before 6.9.3 (the fixed version for 6.9.x) are affected by this vulnerability. This issue can be tracked at: https://jira.atlassian.com/browse/CONFSERVER-57971

 

 

Remote code execution via Widget Connector macro (CVE-2019-3396)

Severity:

Atlassian rates the severity level of this vulnerability as critical, according to the scale published in our Atlassian severity levels. The scale allows us to rank the severity as critical, high, moderate or low. This is our assessment and you should evaluate its applicability to your own IT environment.

 

Description:
There was a server-side template injection vulnerability in Confluence via Widget Connector. An attacker is able to exploit this issue to achieve path traversal and remote code execution on systems that run a vulnerable version of Confluence.

 

Versions of Confluence before version 6.6.12 (the fixed version for 6.6.x), from version 6.7.0 before 6.12.3 (the fixed version for 6.12.x), from version 6.13.0 before 6.13.3 (the fixed version for 6.13.x) and from version 6.14.0 before 6.14.2 (the fixed version for 6.14.x) are affected by this vulnerability. This issue can be tracked at:https://jira.atlassian.com/browse/CONFSERVER-57974 .

 


Fix:

To address these issues, we have released the following versions of
Confluence Server and Data Center containing a fix:

* version 6.6.12
* version 6.12.3
* version 6.13.3
* version 6.14.2

Remediation:

Upgrade Confluence Server and Data Center to version 6.14.2 or higher.

The vulnerabilities and fix versions are described above. If affected, you should upgrade to the latest version immediately.


If you are running Confluence Server and or Data Center 6.6.x and cannot upgrade to 6.14.2, upgrade to version 6.6.12.

If you are running Confluence Server and or Data Center 6.12.x and cannot upgrade to 6.14.2, to version 6.12.3.

If you are running Confluence Server and or Data Center 6.13.x and cannot upgrade to 6.14.2, upgrade to version 6.13.3.



For a full description of the latest version of Confluence Server and Data Center, see the release notes found at https://confluence.atlassian.com/display/DOC/Confluence+Release+Notes. You can download the latest version of Confluence Server and Confluence Data Center from the download centre found at https://www.atlassian.com/software/confluence/download.

 


Support:
If you have questions or concerns regarding this advisory, please raise a
support request at https://support.atlassian.com/.

BZOJ 5381 or & Codeforces 623E Transforming Sequence DP+NTT

BZOJ 5381 or & Codeforces 623E Transforming Sequence DP+NTT

两道题题意都是一样的 不过$CF$的模数是$10^9+7$

很简单的分析发现$A_i$项一定要有一个之前没有出现过的二进制位才能满足条件 考虑$DP$来做

设$f_{i,j}$表示$i$个数用了二进制位上的$j$个位置后满足要求的方案数
转移式为:$f_{a+b,j}=\binom{j}{k} f_{a,k} \times (2^k)^{b}f_{b,j-k}$
即前$a$个数用去$k$位 后$b$个数用去$j-k$位 并且对于之前用过的$k$位也可以随意取
上式可化为：$\frac{ f_{a+b , j } } { j ! } = \frac { f_{ a , k } (2^ k ) ^ b} { k ! } \times \frac{ f_{ b, j - k } } { ( j - k ) ! }$
这个式子很显然可以$NTT$来搞

实现的时候写成类似快速幂的形式就可以过了 对于$CF$的模数 可以写写一个任意模数$FFT$ 算$7$次就可以了(我的精度简直醉了)

$BZOJ5381$

#include<bits/stdc++.h>
using namespace std;
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pa pair<int,int>
#define mod 998244353
#define ll long long
#define mk make_pair
#define pb push_back
#define fi first
#define se second
#define cl(x) memset(x,0,sizeof x)
#ifdef Devil_Gary
#define bug(x) cout<<(#x)<<" "<<(x)<<endl
#define debug(...) fprintf(stderr, __VA_ARGS__)
#else
#define bug(x)
#define debug(...)
#endif

const int INF = 0x7fffffff;
const int N=1e5+5;
int M,l,n,m,A[N],B[N],r[N];
int k,b,f[N],g[N],c[N],fac[N],inv[N],ans;
int poww(int x,int y){
	int ans=1;
	while(y){
		if(y&1) ans=(ll)ans*x%mod;
		y>>=1,x=(ll)x*x%mod; 
	}
	return ans;
} 
void NTT(int*A,int f){
	for(int i=0;i<=M;i++) if(r[i]>i) swap(A[i],A[r[i]]);
	for(int i=1;i<M;i<<=1){
		int wn=poww(3,(mod-1)/i/2);
		if(f==-1) wn=poww(wn,mod-2);
		for(int j=0;j<M;j+=(i<<1)){
			int w=1;
			for(int k=0;k<i;k++,w=(ll)w*wn%mod){
				int x=A[j+k],y=(ll)w*A[i+j+k]%mod;
				A[j+k]=(x+y)%mod,A[i+j+k]=(x+mod-y)%mod;
			}
		}
	}
	if(f==-1){
//		reverse(A+1,A+M);
		int inv=poww(M,mod-2);
		for(int i=0;i<=M;i++) A[i]=(ll)A[i]*inv%mod; 
	}
}
void init(){
	fac[0]=fac[1]=inv[0]=inv[1]=1;
	for(int i=2;i<N;i++) fac[i]=(ll)fac[i-1]*i%mod;
	for(int i=2;i<N;i++) inv[i]=(ll)(mod-mod/i)*inv[mod%i]%mod;
	for(int i=2;i<N;i++) inv[i]=(ll)inv[i]*inv[i-1]%mod;
}
void NTT_MOD(int*a,int*b,int n){
	cl(A),cl(B);
	for(int i=0;i<=n;i++) A[i]=a[i],B[i]=b[i]; 
	NTT(A,1),NTT(B,1);
	for(int i=0;i<M;i++) A[i]=(ll)A[i]*B[i]%mod;
	NTT(A,-1);
	for(int i=0;i<=n;i++) a[i]=A[i];
}
void work(int*a,int*b,int n,int p){
	int t=1;
	cl(c);
	for(int i=0;i<=n;i++) c[i]=(ll)a[i]*t%mod,t=(ll)t*p%mod;
	NTT_MOD(c,b,n);
	memcpy(a,c,sizeof c);
}
int Calc(int n,int m){
	return (ll)fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main(){
#ifdef Devil_Gary
	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
#endif
	cin>>n>>k;
	for(M=1;M<=k+k;M<<=1,l++);
	for(int i=0;i<M;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
	init(),g[0]=1,b=2;
	for(int i=1;i<=k;i++) f[i]=inv[i];
	while(n){
		if(n&1) work(g,f,k,b);
		n>>=1,work(f,f,k,b),b=(ll)b*b%mod;
	}
	for(int i=n;i<=k;i++) (ans+=(ll)g[i]*fac[i]%mod*Calc(k,i)%mod)%=mod;
	printf("%d\n",ans);
}

$CF623E$

#include<bits/stdc++.h>
using namespace std;
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pa pair<int,int>
#define mod 1000000007
#define ll long long
#define mk make_pair
#define pb push_back
#define fi first
#define se second
#define cl(x) memset(x,0,sizeof x)
#ifdef Devil_Gary
#define bug(x) cout<<(#x)<<" "<<(x)<<endl
#define debug(...) fprintf(stderr, __VA_ARGS__)
#else
#define bug(x)
#define debug(...)
#endif

const int INF = 0x7fffffff;
const int N=1e5+5;
struct Cp{
	double x,y;
	Cp (double _x=0,double _y=0) { x=_x,y=_y;}
	Cp operator + (const Cp &ch){ return Cp(x+ch.x,y+ch.y); }
	Cp operator - (const Cp &ch){ return Cp(x-ch.x,y-ch.y); }
	Cp operator * (const Cp &ch){ return Cp(x*ch.x-y*ch.y,x*ch.y+y*ch.x); }
}A[N],B[N],C[N],D[N],w,w0,tmp,wi[16][65536];;
int M,l,r[N];
#define pi acos(-1.0)
void FFT(Cp *A,int f){
	for(int i=0;i<M;i++) if(r[i]>i) swap(A[r[i]],A[i]);
	int gg=0;
	for(int i=1;i<M;i<<=1){
		w.x=cos(pi/i),w.y=sin(pi/i)*f;
		for(int j=0;j<M;j+=(i<<1)){
			for(int k=0;k<i;k++){
				w0=wi[gg][k],w0.y*=f;
				Cp x=A[j+k],y=w0*A[i+j+k];
				A[j+k]=x+y,A[i+j+k]=x-y;
			}
		}
		gg++;
	}
	if(f==-1) for(int i=0;i<M;i++) A[i].x/=M;
}
ll n;
int k,b,f[N],g[N],fac[N],inv[N],ans;
void init(){
	fac[0]=fac[1]=inv[0]=inv[1]=1;
	for(int i=2;i<N;i++) fac[i]=(ll)fac[i-1]*i%mod;
	for(int i=2;i<N;i++) inv[i]=(ll)(mod-mod/i)*inv[mod%i]%mod;
	for(int i=2;i<N;i++) inv[i]=(ll)inv[i]*inv[i-1]%mod;
    int k=0;
    for(int i=2;i<=N;i<<=1){
        for(int j=0;j<i;j++)wi[k][j]=Cp(cos(j*pi/(i/2)),sin(j*pi/(i/2)));
        k++;
    }
}
void FFT_MOD(int*a,int*b,int n){
	cl(A),cl(B),cl(C),cl(D);
	for(int i=0;i<M;i++){
		A[i].x=a[i]>>15;
		B[i].x=a[i]&32767;
		C[i].x=b[i]>>15;
		D[i].x=b[i]&32767;
	}
	FFT(A,1),FFT(B,1),FFT(C,1),FFT(D,1);
	for(int i=0;i<M;i++){
		tmp=A[i]*D[i]+B[i]*C[i];
		A[i]=A[i]*C[i];
		C[i]=B[i]*D[i];
		B[i]=tmp;
	}
	FFT(A,-1),FFT(B,-1),FFT(C,-1),cl(a);	
	for(int i=0;i<=n;i++)a[i]=((llround(A[i].x)%mod<<30)+(llround(B[i].x)%mod<<15)+llround(C[i].x)%mod)%mod;
}
int c[N];
void work(int*a,int*b,int n,int p){
	int t=1;
	cl(c);
	for(int i=0;i<=n;i++) c[i]=(ll)a[i]*t%mod,t=(ll)t*p%mod;
	FFT_MOD(c,b,n);
	memcpy(a,c,sizeof c);
}
int Calc(int n,int m){
	return (ll)fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main(){
#ifdef Devil_Gary
	freopen("in.txt","r",stdin);
	freopen("out.txt","w",stdout);
#endif
	cin>>n>>k;
	if(n>k) return puts("0"),0;
	for(M=1;M<=k+k;M<<=1,l++);
	for(int i=0;i<M;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
	init(),g[0]=1,b=2;
	for(int i=1;i<=k;i++) f[i]=inv[i];
	while(n){
		if(n&1) work(g,f,k,b);
		n>>=1,work(f,f,k,b),b=(ll)b*b%mod;
	}
	for(int i=n;i<=k;i++) (ans+=(ll)g[i]*fac[i]%mod*Calc(k,i)%mod)%=mod;
	printf("%d\n",ans);
}

我们今天的关于ZOJ Monthly, January 2019 I Little Sub and Isomorphism Sequences(set 妙用) ZOJ4089的分享已经告一段落，感谢您的关注，如果您想了解更多关于2018ICPC青岛区域赛 zoj4062 Plants vs. Zombies、2019山东ACM省赛K题 zoj4123 Happy Equation、Atlassian - Confluence Security Advisory - 2019-03-20、BZOJ 5381 or & Codeforces 623E Transforming Sequence DP+NTT的相关信息，请在本站查询。

本文标签：

上一篇Linux字符串截取和处理命令 cut、printf、awk、sed、sort、wc（linux中字符串截取）

下一篇安装 docker docker-composer lnmp 一键安装包 --DNMP（安装docker教程）

相关文章