本文将分享NumPy-为二维数组排序的np.search的详细内容,并且还将对numpy二维数组排序进行详尽解释,此外,我们还将为大家带来关于"二分查找(BinarySearch)"与"斐波那契查找(
本文将分享NumPy-为二维数组排序的np.search的详细内容,并且还将对numpy 二维数组排序进行详尽解释,此外,我们还将为大家带来关于"二分查找 (Binary Search)" 与 "斐波那契查找 (Fibonacci Search)"、/search 'search' 对象的 AttributeError 没有属性 'cleaned_data' django、2019-ICCV-Progressive Differentiable Architecture Search Bridging the Depth Gap Between Search an...、700. Search in a Binary Search Tree的相关知识,希望对你有所帮助。
本文目录一览:- NumPy-为二维数组排序的np.search(numpy 二维数组排序)
- "二分查找 (Binary Search)" 与 "斐波那契查找 (Fibonacci Search)"
- /search 'search' 对象的 AttributeError 没有属性 'cleaned_data' django
- 2019-ICCV-Progressive Differentiable Architecture Search Bridging the Depth Gap Between Search an...
- 700. Search in a Binary Search Tree
NumPy-为二维数组排序的np.search(numpy 二维数组排序)
我创建了一些更高级的策略。
还实现了像another my answer中那样使用tuples的简单策略。
测量所有溶液的时间。
大多数策略都使用np.searchsorted作为基础引擎。为了实现这些高级策略,使用了特殊的包装类_CmpIx来为__lt__调用提供自定义比较功能(np.searchsorted)。
-
py.tuples策略只是将所有列转换为元组,并将其存储为np.object_dtype的numpy 1D数组,然后进行常规搜索排序。 -
py.zip使用python的zip懒惰地执行相同的任务。 -
np.lexsort策略仅使用np.lexsort来按字典顺序比较两列。 -
np.nonzero使用np.flatnonzero(a != b)表达式。 -
cmp_numba在_CmpIx包装器内使用ahead of time编译的numba代码,以便按字典顺序快速比较两个提供的元素。 -
np.searchsorted使用标准的numpy函数,但仅针对一维情况进行测量。 - 对于
numba策略,整个搜索算法是使用Numba引擎从头开始实现的,算法基于binary search。此算法有_py和_nm个变体,_nm更快,因为它使用Numba编译器,而_py是相同的算法,但未编译。还有_sorted种风味,它已经对要插入的数组进行了额外的优化,已经排序。 -
view1d-@MadPhysicist in this answer建议的方法。用代码注释掉它们,因为对于大多数键长度> 1的大多数测试,它们返回错误的答案,这可能是由于原始查看数组的某些问题造成的。
Try it online!
class SearchSorted2D:
class _CmpIx:
def __init__(self,t,p,i):
self.p,self.i = p,i
self.leg = self.leg_cache()[t]
self.lt = lambda o: self.leg(self,o,False) if self.i != o.i else False
self.le = lambda o: self.leg(self,True) if self.i != o.i else True
@classmethod
def leg_cache(cls):
if not hasattr(cls,'leg_cache_data'):
cls.leg_cache_data = {
'py.zip': cls._leg_py_zip,'np.lexsort': cls._leg_np_lexsort,'np.nonzero': cls._leg_np_nonzero,'cmp_numba': cls._leg_numba_create(),}
return cls.leg_cache_data
def __eq__(self,o): return not self.lt(o) and self.le(o)
def __ne__(self,o): return self.lt(o) or not self.le(o)
def __lt__(self,o): return self.lt(o)
def __le__(self,o): return self.le(o)
def __gt__(self,o): return not self.le(o)
def __ge__(self,o): return not self.lt(o)
@staticmethod
def _leg_np_lexsort(self,eq):
import numpy as np
ia,ib = (self.i,o.i) if eq else (o.i,self.i)
return (np.lexsort(self.p.ab[::-1,ia : (ib + (-1,1)[ib >= ia],None)[ib == 0] : ib - ia])[0] == 0) == eq
@staticmethod
def _leg_py_zip(self,eq):
for l,r in zip(self.p.ab[:,self.i],self.p.ab[:,o.i]):
if l < r:
return True
if l > r:
return False
return eq
@staticmethod
def _leg_np_nonzero(self,eq):
import numpy as np
a,b = self.p.ab[:,o.i]
ix = np.flatnonzero(a != b)
return a[ix[0]] < b[ix[0]] if ix.size != 0 else eq
@staticmethod
def _leg_numba_create():
import numpy as np
try:
from numba.pycc import CC
cc = CC('ss_numba_mod')
@cc.export('ss_numba_i8','b1(i8[:],i8[:],b1)')
def ss_numba(a,b,eq):
for i in range(a.size):
if a[i] < b[i]:
return True
elif b[i] < a[i]:
return False
return eq
cc.compile()
success = True
except:
success = False
if success:
try:
import ss_numba_mod
except:
success = False
def odo(self,eq):
a,o.i]
assert a.ndim == 1 and a.shape == b.shape,(a.shape,b.shape)
return ss_numba_mod.ss_numba_i8(a,eq)
return odo if success else None
def __init__(self,type_):
import numpy as np
self.type_ = type_
self.ci = np.array([],dtype = np.object_)
def __call__(self,a,*pargs,**nargs):
import numpy as np
self.ab = np.concatenate((a,b),axis = 1)
self._grow(self.ab.shape[1])
ix = np.searchsorted(self.ci[:a.shape[1]],self.ci[a.shape[1] : a.shape[1] + b.shape[1]],**nargs)
return ix
def _grow(self,to):
import numpy as np
if self.ci.size >= to:
return
import math
to = 1 << math.ceil(math.log(to) / math.log(2))
self.ci = np.concatenate((self.ci,[self._CmpIx(self.type_,self,i) for i in range(self.ci.size,to)]))
class SearchSorted2DNumba:
@classmethod
def do(cls,v,side = 'left',*,vsorted = False,numba_ = True):
import numpy as np
if not hasattr(cls,'_ido_numba'):
def _ido_regular(a,vsorted,lrt):
nk,na,nb = a.shape[0],a.shape[1],b.shape[1]
res = np.zeros((2,nb),dtype = np.int64)
max_depth = 0
if nb == 0:
return res,max_depth
#lb,le,rb,re = 0,0
lrb,lre = 0,0
if vsorted:
brngs = np.zeros((nb,6),dtype = np.int64)
brngs[0,:4] = (-1,nb >> 1,nb)
i,j,size = 0,1,1
while i < j:
for k in range(i,j):
cbrng = brngs[k]
bp,bb,bm,be = cbrng[:4]
if bb < bm:
brngs[size,:4] = (k,(bb + bm) >> 1,bm)
size += 1
bmp1 = bm + 1
if bmp1 < be:
brngs[size,bmp1,(bmp1 + be) >> 1,be)
size += 1
i,j = j,size
assert size == nb
brngs[:,4:] = -1
for ibc in range(nb):
if not vsorted:
ib,lrb,lre = ibc,na
else:
ibpi,ib = int(brngs[ibc,0]),int(brngs[ibc,2])
if ibpi == -1:
lrb,na
else:
ibp = int(brngs[ibpi,2])
if ib < ibp:
lrb,lre = int(brngs[ibpi,4]),int(res[1,ibp])
else:
lrb,lre = int(res[0,ibp]),int(brngs[ibpi,5])
brngs[ibc,4 : 6] = (lrb,lre)
assert lrb != -1 and lre != -1
for ik in range(nk):
if lrb >= lre:
if ik > max_depth:
max_depth = ik
break
bv = b[ik,ib]
# Binary searches
if nk != 1 or lrt == 2:
cb,ce = lrb,lre
while cb < ce:
cm = (cb + ce) >> 1
av = a[ik,cm]
if av < bv:
cb = cm + 1
elif bv < av:
ce = cm
else:
break
lrb,lre = cb,ce
if nk != 1 or lrt >= 1:
cb,lre
while cb < ce:
cm = (cb + ce) >> 1
if not (bv < a[ik,cm]):
cb = cm + 1
else:
ce = cm
#rb,re = cb,ce
lre = ce
if nk != 1 or lrt == 0 or lrt == 2:
cb,lre
while cb < ce:
cm = (cb + ce) >> 1
if a[ik,cm] < bv:
cb = cm + 1
else:
ce = cm
#lb,le = cb,ce
lrb = cb
#lrb,lre = lb,re
res[:,ib] = (lrb,lre)
return res,max_depth
cls._ido_regular = _ido_regular
import numba
cls._ido_numba = numba.jit(nopython = True,nogil = True,cache = True)(cls._ido_regular)
assert side in ['left','right','left_right'],side
a,v = np.array(a),np.array(v)
assert a.ndim == 2 and v.ndim == 2 and a.shape[0] == v.shape[0],v.shape)
res,max_depth = (cls._ido_numba if numba_ else cls._ido_regular)(
a,{'left': 0,'right': 1,'left_right': 2}[side],)
return res[0] if side == 'left' else res[1] if side == 'right' else res
def Test():
import time
import numpy as np
np.random.seed(0)
def round_float_fixed_str(x,n = 0):
if type(x) is int:
return str(x)
s = str(round(float(x),n))
if n > 0:
s += '0' * (n - (len(s) - 1 - s.rfind('.')))
return s
def to_tuples(x):
r = np.empty([x.shape[1]],dtype = np.object_)
r[:] = [tuple(e) for e in x.T]
return r
searchsorted2d = {
'py.zip': SearchSorted2D('py.zip'),'np.nonzero': SearchSorted2D('np.nonzero'),'np.lexsort': SearchSorted2D('np.lexsort'),'cmp_numba': SearchSorted2D('cmp_numba'),}
for iklen,klen in enumerate([1,2,5,10,20,50,100,200]):
times = {}
for side in ['left','right']:
a = np.zeros((klen,0),dtype = np.int64)
tac = to_tuples(a)
for itest in range((15,100)[iklen == 0]):
b = np.random.randint(0,(3,100000)[iklen == 0],(klen,np.random.randint(1,(1000,2000)[iklen == 0])),dtype = np.int64)
b = b[:,np.lexsort(b[::-1])]
if iklen == 0:
assert klen == 1,klen
ts = time.time()
ix1 = np.searchsorted(a[0],b[0],side = side)
te = time.time()
times['np.searchsorted'] = times.get('np.searchsorted',0.) + te - ts
for cached in [False,True]:
ts = time.time()
tb = to_tuples(b)
ta = tac if cached else to_tuples(a)
ix1 = np.searchsorted(ta,tb,side = side)
if not cached:
ix0 = ix1
tac = np.insert(tac,ix0,tb) if cached else tac
te = time.time()
timesk = f'py.tuples{("","_cached")[cached]}'
times[timesk] = times.get(timesk,0.) + te - ts
for type_ in searchsorted2d.keys():
if iklen == 0 and type_ in ['np.nonzero','np.lexsort']:
continue
ss = searchsorted2d[type_]
try:
ts = time.time()
ix1 = ss(a,side = side)
te = time.time()
times[type_] = times.get(type_,0.) + te - ts
assert np.array_equal(ix0,ix1)
except Exception:
times[type_ + '!failed'] = 0.
for numba_ in [False,True]:
for vsorted in [False,True]:
if numba_:
# Heat-up/pre-compile numba
SearchSorted2DNumba.do(a,side = side,vsorted = vsorted,numba_ = numba_)
ts = time.time()
ix1 = SearchSorted2DNumba.do(a,numba_ = numba_)
te = time.time()
timesk = f'numba{("_py","_nm")[numba_]}{("","_sorted")[vsorted]}'
times[timesk] = times.get(timesk,ix1)
# View-1D methods suggested by @MadPhysicist
if False: # Commented out as working just some-times
aT,bT = np.copy(a.T),np.copy(b.T)
assert aT.ndim == 2 and bT.ndim == 2 and aT.shape[1] == klen and bT.shape[1] == klen,(aT.shape,bT.shape,klen)
for ty in ['if','cf']:
try:
dt = np.dtype({'if': [('',b.dtype)] * klen,'cf': [('row',b.dtype,klen)]}[ty])
ts = time.time()
va = np.ndarray(aT.shape[:1],dtype = dt,buffer = aT)
vb = np.ndarray(bT.shape[:1],buffer = bT)
ix1 = np.searchsorted(va,vb,side = side)
te = time.time()
assert np.array_equal(ix0,ix1),(ix0.shape,ix1.shape,ix0[:20],ix1[:20])
times[f'view1d_{ty}'] = times.get(f'view1d_{ty}',0.) + te - ts
except Exception:
raise
a = np.insert(a,axis = 1)
stimes = ([f'key_len: {str(klen).rjust(3)}'] +
[f'{k}: {round_float_fixed_str(v,4).rjust(7)}' for k,v in times.items()])
nlines = 4
print('-' * 50 + '\n' + ('','!LARGE!:\n')[iklen == 0],end = '')
for i in range(nlines):
print(','.join(stimes[len(stimes) * i // nlines : len(stimes) * (i + 1) // nlines]),flush = True)
Test()
输出:
--------------------------------------------------
!LARGE!:
key_len: 1,np.searchsorted: 0.0250
py.tuples_cached: 3.3113,py.tuples: 30.5263,py.zip: 40.9785
cmp_numba: 25.7826,numba_py: 3.6673
numba_py_sorted: 6.8926,numba_nm: 0.0466,numba_nm_sorted: 0.0505
--------------------------------------------------
key_len: 1,py.tuples_cached: 0.1371
py.tuples: 0.4698,py.zip: 1.2005,np.nonzero: 4.7827
np.lexsort: 4.4672,cmp_numba: 1.0644,numba_py: 0.2748
numba_py_sorted: 0.5699,numba_nm: 0.0005,numba_nm_sorted: 0.0020
--------------------------------------------------
key_len: 2,py.tuples_cached: 0.1131
py.tuples: 0.3643,py.zip: 1.0670,np.nonzero: 4.5199
np.lexsort: 3.4595,cmp_numba: 0.8582,numba_py: 0.4958
numba_py_sorted: 0.6454,numba_nm: 0.0025,numba_nm_sorted: 0.0025
--------------------------------------------------
key_len: 5,py.tuples_cached: 0.1876
py.tuples: 0.4493,py.zip: 1.6342,np.nonzero: 5.5168
np.lexsort: 4.6086,cmp_numba: 1.0939,numba_py: 1.0607
numba_py_sorted: 0.9737,numba_nm: 0.0050,numba_nm_sorted: 0.0065
--------------------------------------------------
key_len: 10,py.tuples_cached: 0.6017
py.tuples: 1.2275,py.zip: 3.5276,np.nonzero: 13.5460
np.lexsort: 12.4183,cmp_numba: 2.5404,numba_py: 2.8334
numba_py_sorted: 2.3991,numba_nm: 0.0165,numba_nm_sorted: 0.0155
--------------------------------------------------
key_len: 20,py.tuples_cached: 0.8316
py.tuples: 1.3759,py.zip: 3.4238,np.nonzero: 13.7834
np.lexsort: 16.2164,cmp_numba: 2.4483,numba_py: 2.6405
numba_py_sorted: 2.2226,numba_nm: 0.0170,numba_nm_sorted: 0.0160
--------------------------------------------------
key_len: 50,py.tuples_cached: 1.0443
py.tuples: 1.4085,py.zip: 2.2475,np.nonzero: 9.1673
np.lexsort: 19.5266,cmp_numba: 1.6181,numba_py: 1.7731
numba_py_sorted: 1.4637,numba_nm: 0.0415,numba_nm_sorted: 0.0405
--------------------------------------------------
key_len: 100,py.tuples_cached: 2.0136
py.tuples: 2.5380,py.zip: 2.2279,np.nonzero: 9.2929
np.lexsort: 33.9505,cmp_numba: 1.5722,numba_py: 1.7158
numba_py_sorted: 1.4208,numba_nm: 0.0871,numba_nm_sorted: 0.0851
--------------------------------------------------
key_len: 200,py.tuples_cached: 3.5945
py.tuples: 4.1847,py.zip: 2.3553,np.nonzero: 11.3781
np.lexsort: 66.0104,cmp_numba: 1.8153,numba_py: 1.9449
numba_py_sorted: 1.6463,numba_nm: 0.1661,numba_nm_sorted: 0.1651
从计时numba_nm来看,实施是最快的,它的表现快于次快的(py.zip或py.tuples_cached)15-100x次。对于一维案例,它具有与标准1.85x相当的速度(np.searchsorted较慢)。同样,看来_sorted的风格并不能改善情况(即使用有关正在排序的插入数组的信息)。
cmp_numba方法似乎比执行相同算法但使用纯python的1.5x平均快py.zip倍。由于平均最大等键深度约为15-18个元素,因此numba在这里不会获得太大的提速。如果深度为数百,则numba代码可能会大大提高速度。
py.tuples_cached策略在密钥长度为py.zip的情况下比<= 100快。
而且看来np.lexsort实际上很慢,要么没有针对两列进行优化,要么花费了一些时间进行预处理(例如将行拆分为列表),或者懒字典比较,最后一种情况可能是真正的原因,因为lexsort随着密钥长度的增长而变慢。
策略np.nonzero也不是懒惰的,因此也很慢,并且随着密钥长度的增长而变慢(但是变慢的速度不如np.lexsort那样。)
上面的时间可能不太准确,因为我的CPU每次过热都会随机降低内核频率2-2.3倍,并且由于它是笔记本电脑中的强大CPU而经常过热。
,这里有两件事可以为您提供帮助:(1)您可以对结构化数组进行排序和搜索,(2)如果您具有可以映射为整数的有限集合,则可以利用它来发挥自己的优势。
以1D模式查看
假设您要插入一个字符串数组:
data = np.array([['a','1'],['a','z'],['b','a']],dtype=object)
由于数组从不参差不齐,因此您可以构造一个与行大小相同的dtype:
dt = np.dtype([('',data.dtype)] * data.shape[1])
使用我无耻插入的答案here,您现在可以将原始2D数组查看为1D:
view = np.ndarray(data.shape[:1],dtype=dt,buffer=data)
现在可以完全直接地进行搜索了:
key = np.array([('a','a')],dtype=dt)
index = np.searchsorted(view,key)
您甚至可以使用适当的最小值找到不完整元素的插入索引。对于字符串,它将为''。
如果您不必检查dtype的每个字段,则可以从比较中获得更好的里程。您可以使用单个齐次字段创建相似的dtype:
dt2 = np.dtype([('row',data.dtype,data.shape[1])])
构造视图与以前相同:
view = np.ndarray(data.shape[:1],dtype=dt2,buffer=data)
这次的按键操作有所不同(另一个插头here):
key = np.array([(['a','a'],)],dtype=dt2)
使用以下方法对对象施加的排序顺序不正确:Sorting array of objects by row using custom dtype。如果链接的问题有解决方法,我在这里留下参考。另外,它在对整数排序时仍然非常有用。
整数映射
如果要搜索的对象数量有限,则将它们映射为整数会更容易:
idata = np.empty(data.shape,dtype=int)
keys = [None] * data.shape[1] # Map index to key per column
indices = [None] * data.shape[1] # Map key to index per column
for i in range(data.shape[1]):
keys[i],idata[:,i] = np.unique(data[:,i],return_inverse=True)
indices[i] = {k: i for i,k in enumerate(keys[i])} # Assumes hashable objects
idt = np.dtype([('row',idata.dtype,idata.shape[1])])
view = idata.view(idt).ravel()
仅当data实际上在每一列中包含所有可能的键时,此方法才有效。否则,您将不得不通过其他方式获取正向和反向映射。一旦建立起来,设置密钥就简单得多,只需要indices:
key = np.array([index[k] for index,k in zip(indices,'a'])])
进一步的改进
如果您拥有的类别数量为八个或更少,并且每个类别具有256个或更少的元素,则可以通过将所有内容放入单个np.uint64元素左右来构造更好的哈希。
k = math.ceil(math.log(data.shape[1],2)) # math.log provides base directly
assert 0 < k <= 64
idata = np.empty((data.shape[:1],k),dtype=np.uint8)
...
idata = idata.view(f'>u{k}').ravel()
键的制作方法也与此类似:
key = np.array([index[k] for index,'a'])]).view(f'>u{k}')
定时
我已经使用随机随机排列的字符串为此处显示的方法(没有其他答案)计时。关键的计时参数是:
-
M:行数:10 ** {2,3,4,5} -
N:列数:2 ** {3、4、5、6} -
K:要插入的元素数:1,M // 10 - 方法:
individual_fields,combined_field,int_mapping,int_packing。功能如下所示。
对于后两种方法,我假设您将数据预先转换为映射的dtype,而不是搜索键。因此,我要传递转换后的数据,但要安排键的转换时间。
import numpy as np
from math import ceil,log
def individual_fields(data,keys):
dt = [('',data.dtype)] * data.shape[1]
dview = np.ndarray(data.shape[:1],buffer=data)
kview = np.ndarray(keys.shape[:1],buffer=keys)
return np.searchsorted(dview,kview)
def combined_fields(data,keys):
dt = [('row',data.shape[1])]
dview = np.ndarray(data.shape[:1],kview)
def int_mapping(idata,keys,indices):
idt = np.dtype([('row',idata.shape[1])])
dview = idata.view(idt).ravel()
kview = np.empty(keys.shape[0],dtype=idt)
for i,(index,key) in enumerate(zip(indices,keys.T)):
kview['row'][:,i] = [index[k] for k in key]
return np.searchsorted(dview,kview)
def int_packing(idata,indices):
idt = f'>u{idata.shape[1]}'
dview = idata.view(idt).ravel()
kview = np.empty(keys.shape,dtype=np.uint8)
for i,keys.T)):
kview[:,i] = [index[k] for k in key]
kview = kview.view(idt).ravel()
return np.searchsorted(dview,kview)
时间码:
from math import ceil,log
from string import ascii_lowercase
from timeit import Timer
def time(m,n,k,fn,*args):
t = Timer(lambda: fn(*args))
s = t.autorange()[0]
print(f'M={m}; N={n}; K={k} {fn.__name__}: {min(t.repeat(5,s)) / s}')
selection = np.array(list(ascii_lowercase),dtype=object)
for lM in range(2,6):
M = 10**lM
for lN in range(3,6):
N = 2**lN
data = np.random.choice(selection,size=(M,N))
np.ndarray(data.shape[0],dtype=[('',data.dtype)] * data.shape[1],buffer=data).sort()
idata = np.array([[ord(a) - ord('a') for a in row] for row in data],dtype=np.uint8)
ikeys = [selection] * data.shape[1]
indices = [{k: i for i,k in enumerate(selection)}] * data.shape[1]
for K in (1,M // 10):
key = np.random.choice(selection,size=(K,N))
time(M,N,K,individual_fields,data,key)
time(M,combined_fields,int_mapping,idata,key,indices)
if N <= 8:
time(M,int_packing,indices)
结果:
M = 100(units = us)
| K |
+---------------------------+---------------------------+
N | 1 | 10 |
+------+------+------+------+------+------+------+------+
| IF | CF | IM | IP | IF | CF | IM | IP |
---+------+------+------+------+------+------+------+------+
8 | 25.9 | 18.6 | 52.6 | 48.2 | 35.8 | 22.7 | 76.3 | 68.2 |
16 | 40.1 | 19.0 | 87.6 | -- | 51.1 | 22.8 | 130. | -- |
32 | 68.3 | 18.7 | 157. | -- | 79.1 | 22.4 | 236. | -- |
64 | 125. | 18.7 | 290. | -- | 135. | 22.4 | 447. | -- |
---+------+------+------+------+------+------+------+------+
M = 1000(units = us)
| K |
+---------------------------+---------------------------+---------------------------+
N | 1 | 10 | 100 |
+------+------+------+------+------+------+------+------+------+------+------+------+
| IF | CF | IM | IP | IF | CF | IM | IP | IF | CF | IM | IP |
---+------+------+------+------+------+------+------+------+------+------+------+------+
8 | 26.9 | 19.1 | 55.0 | 55.0 | 44.8 | 25.1 | 79.2 | 75.0 | 218. | 74.4 | 305. | 250. |
16 | 41.0 | 19.2 | 90.5 | -- | 59.3 | 24.6 | 134. | -- | 244. | 79.0 | 524. | -- |
32 | 68.5 | 19.0 | 159. | -- | 87.4 | 24.7 | 241. | -- | 271. | 80.5 | 984. | -- |
64 | 128. | 19.7 | 312. | -- | 168. | 26.0 | 549. | -- | 396. | 7.78 | 2.0k | -- |
---+------+------+------+------+------+------+------+------+------+------+------+------+
M = 10K(units = us)
| K |
+---------------------------+---------------------------+---------------------------+
N | 1 | 10 | 1000 |
+------+------+------+------+------+------+------+------+------+------+------+------+
| IF | CF | IM | IP | IF | CF | IM | IP | IF | CF | IM | IP |
---+------+------+------+------+------+------+------+------+------+------+------+------+
8 | 28.8 | 19.5 | 54.5 | 107. | 57.0 | 27.2 | 90.5 | 128. | 3.2k | 762. | 2.7k | 2.1k |
16 | 42.5 | 19.6 | 90.4 | -- | 73.0 | 27.2 | 140. | -- | 3.3k | 752. | 4.6k | -- |
32 | 73.0 | 19.7 | 164. | -- | 104. | 26.7 | 246. | -- | 3.4k | 803. | 8.6k | -- |
64 | 135. | 19.8 | 302. | -- | 162. | 26.1 | 466. | -- | 3.7k | 791. | 17.k | -- |
---+------+------+------+------+------+------+------+------+------+------+------+------+
individual_fields(IF)通常是最快的工作方法。它的复杂度与列数成正比。不幸的是combined_fields(CF)不适用于对象数组。否则,它不仅是最快的方法,而且不会随着列数的增加而变得复杂。
我认为会更快的所有技术都不是,因为将python对象映射到键很慢(例如,打包int数组的实际查找比结构化数组快得多)。
参考
这是我要使代码完全起作用的其他问题:
- View object array under different dtype
- Creating array with single structured element containing an array
- Sorting array of objects by row using custom dtype
发布我在问题中提到的第一个幼稚的解决方案,它只是将2D数组转换为包含原始列作为Python元组的dtype = np.object_的1D数组,然后使用1D np.searchsorted,该解决方案适用于任何{{ 1}}。实际上,按照我对当前问题的另一种回答,该解决方案并不是那么幼稚,而是相当快的,尤其是对于长度小于100的键来说,它是快速的。
Try it online!
dtype
"二分查找 (Binary Search)" 与 "斐波那契查找 (Fibonacci Search)"
首先,我们来看一个笔者的拙作,一段二分查找代码
//返回值是key的下标,如果A中不存在key则返回-1
template <class T>
int BinSearch(T* A, const T &key, int lo, int hi)
{
int mid;
while(lo<hi)
{
mid = lo + (hi-lo)/2;
if(key < A[mid])
hi = mid-1;
else if(key > A[mid])
lo = mid+1;
else
return mid;
if(lo==hi && A[lo]==key)
return lo;
}
return -1;
} 可以证明,算法的时间复杂度为 O (nlogn),考虑前面的系数的话,大致是 O (1.5nlogn)。
但是,这一实现仍有改进的余地。注意到循环只需要 1 次判断来决定是否转进到左侧,但需要 2 次判断来决定是否转进到右侧。也就是进入左、右分支前的关键码比较次数不等。
而斐波那契查找正是优化了这点。利用斐波那契数来对传入的数组进行黄金分割,这样前半部分较多而后半部分较少。另外,进入前半部分继续搜索所需的判断只有一次,而进入后半部分继续搜索所需的判断却有两次。如此而来,我们人为造成的这种不平衡,反倒是助长了搜索成本的平衡。
template <class T>
int FibSearch(T* A, const T &key, int lo, int hi)
{
int mid;
Fib fib(hi-lo); //构造一个斐波那契数的类
while(lo<hi)
{
int len = hi-lo;
while(fib.get()>len)
fib.prev(); //如果当前的fib.get()返回值大于len,则取前一个斐波那契数
mid = lo + fib.get() - 1; //分割节点的下标
if(key < A[mid])
hi = mid-1;
else if(key > A[mid])
lo = mid+1;
else
return mid;
if(lo==hi && A[lo]==key)
return lo;
}
return -1;
} 这里我们需要构造一个斐波那契数的类。要写好这个类,其实只需要一个数组,用动态规划的算法很好写,这里不再赘述。
既然算法实现好了,我们就对这两种算法的正确性做个小测试吧:
int main()
{
a=0,b=0;
for(int i=0; i<=NUM; ++i)
{
A[i] = i;
}
for(int i=0; i<=NUM; ++i) //正确性验证
{
if( BinSearch(A,i,0,NUM) != FibSearch(A,i,0,NUM) )
{
cout<<"What a fucking day !" <<i<<endl;
}
}
return 0;
} 算法性能对比 (by fovwin):
参考资料:1. 清华大学 MOOC 《数据结构与算法》 by 邓俊辉,第二章
2.Wikipedia - Fibonacci Search Technique (https://en.wikipedia.org/wiki/Fibonacci_search_technique)
3.《"斐波那契查找" 真的比二分查找快么?》 by forwin (强烈推荐,C 语言实现,代码注释非常清晰 - http://blog.csdn.net/fovwin/article/details/9077017)

/search 'search' 对象的 AttributeError 没有属性 'cleaned_data' django
如何解决/search ''search'' 对象的 AttributeError 没有属性 ''cleaned_data'' django?
def searchform(request):
if request.method == "POST":
form1 = search(request.POST)
if form1.is_valid :
titl = form1.cleaned_data.get("query")
top = False
for i in util.list_entries():
if titl == i:
htmlconvo = util.get_entry(titl)
mdcovo = markdowner.convert(htmlconvo)
top = True
break
if top :
return HttpResponseRedirect(request,"encyclopedia/title.html",{
"form":form1,"content":mdcovo,"title": titl
})
else:
lst = []
for j in util.list_entries():
if titl in j:
lst.append(j)
if len(lst) == 0:
form1 = search()
return render(request,"encyclopedia/error.html",{
''form'': form1,})
else:
return render(request,"encyclopedia/index.html",{
"entries": lst,"form": form1})
else:
form1 = search()
return render(request,{
"form":form1,})
这是搜索的视图代码,其中我在 /search 处收到错误 AttributeError “搜索”对象没有属性“cleaned_data” 我该怎么办
<form action="{% url ''search'' %}" method="POST">
{% csrf_token %}
<input type="text" name="search" placeholder="Search Encyclopedia">
</form>
这是我的 layout.html
解决方法
暂无找到可以解决该程序问题的有效方法,小编努力寻找整理中!
如果你已经找到好的解决方法,欢迎将解决方案带上本链接一起发送给小编。
小编邮箱:dio#foxmail.com (将#修改为@)

2019-ICCV-Progressive Differentiable Architecture Search Bridging the Depth Gap Between Search an...
P-DARTS
2019-ICCV-Progressive Differentiable Architecture Search Bridging the Depth Gap Between Search and Evaluation
- Tongji University && Huawei
- GitHub: 200+ stars
- Citation:49
Motivation
Question:
- DARTS has to search the architecture in a shallow network while evaluate in a deeper one.
- DARTS在浅层网络上搜索,在深层网络上评估(cifar search in 8-depth, eval in 20-depth)。
- This brings an issue named the depth gap (see Figure 1(a)), which means that the search stage finds some operations that work well in a shallow architecture, but the evaluation stage actually prefers other operations that fit a deep architecture better.
-

- Such gap hinders these approaches in their application to more complex visual recognition tasks.
Contribution
- propose Progressive DARTS (P-DARTS), a novel and efficient algorithm to bridge the depth gap.
Bring two questions:
Q1: While a deeper architecture requires heavier computational overhead
- we propose search space approximation which, as the depth increases, reduces the number of candidates (operations) according to their scores in the elapsed search process.
Q2:Another issue, lack of stability, emerges with searching over a deep architecture, in which the algorithm can be biased heavily towards skip-connect as it often leads to rapidest error decay during optimization, but, actually, a better option often resides in learnable operations such as convolution.
- we propose search space regularization, which (i) introduces operation-level Dropout [25] to alleviate the dominance of skip-connect during training, and (ii) controls the appearance of skip-connect during evaluation.
Method
search space approximation
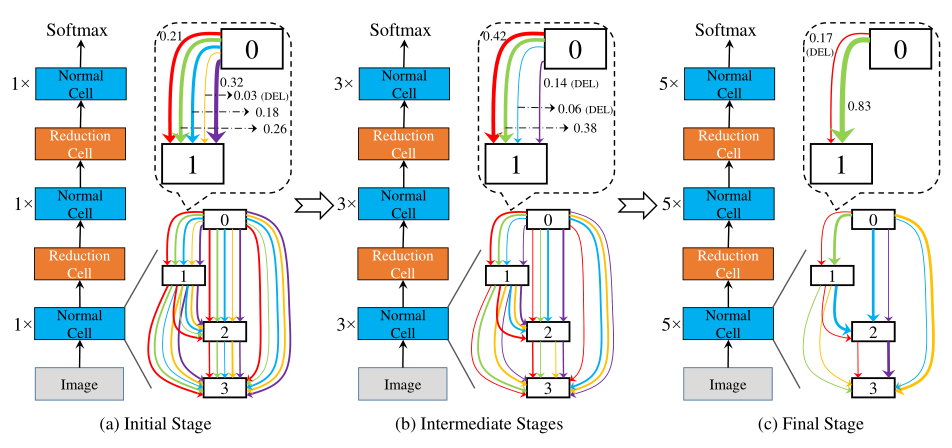
在初始阶段,搜索网络相对较浅,但是cell中每条边上的候选操作最多(所有操作)。在阶段 \(S_{k-1}\)中,根据学习到的网络结构参数(权值)来排序并筛选出权值(重要性)较高的 \(O_k\) 个操作,并由此搭建一个拥有 \(L_k\) 个cell的搜索网络用于下一阶段的搜索,其中, \(L_k > L_{k-1} , O_k < O_{k-1}\) .
这个过程可以渐进而持续地增加搜索网络的深度,直到足够接近测试网络深度。
search space regularization
we observe that information prefers to flow through skip-connect instead of convolution or pooling, which is arguably due to the reason that skip-connect often leads to rapid gradient descent.
实验结果表明在本文采用的框架下,信息往往倾向于通过skip-connect流动,而不是卷积。这是因为skip-connect通常处在梯度下降最速的路径上。
the search process tends to generate architectures with many skip-connect operations, which limits the number of learnable parameters and thus produces unsatisfying performance at the evaluation stage.
在这种情况下,最终搜索得到的结构往往包含大量的skip-connect操作,可训练参数较少,从而使得性能下降。
We address this problem by search space regularization, which consists of two parts.
First, we insert operation-level Dropout [25] after each skip-connect operation, so as to partially ‘cut off’ the straightforward path through skip-connect, and facilitate the algorithm to explore other operations.
However, if we constantly block the path through skip-connect, the algorithm will drop them by assigning low weights to them, which is harmful to the final performance.
然而,持续地阻断这些路径的话会导致在最终生成结构的时候skip-connect操作仍然受到抑制,可能会影响最终性能。
we gradually decay the Dropout rate during the training process in each search stage, thus the straightforward path through skip-connect is blocked at the beginning and treated equally afterward when parameters of other operations are well learned, leaving the algorithm itself to make the decision.
因此,作者在训练的过程中逐渐地衰减Dropout的概率,在训练初期施加较强的Dropout,在训练后期将其衰减到很轻微的程度,使其不影响最终的网络结构参数的学习。
Despite the use of Dropout, we still observe that skip-connect, as a special kind of operation, has a significant impact on recognition accuracy at the evaluation stage.
另一方面,尽管使用了Operations层面的Dropout,作者依然观察到了skip-connect操作对实验性能的强烈影响。
This motivates us to design the second regularization rule, architecture refinement, which simply controls the number of preserved skip-connects, after the final search stage, to be a constant M.
因此,作者提出第二个搜索空间正则方法,即在最终生成的网络结构中,保留固定数量的skip-connect操作。具体的,作者根据最终阶段的结构参数,只保留权值最大的M个skip-connect操作,这一正则方法保证了搜索过程的稳定性。在本文中, M=2 .
We emphasize that the second regularization technique must be applied on top of the first one, otherwise, in the situations without operation-level Dropout, the search process is producing low-qualityarchitectureweights, basedon which we could not build up a powerful architecture even with a fixed number of skip-connects.
需要强调的是,第二种搜索空间正则是建立在第一种搜索空间正则的基础上的。在没有执行第一种正则的情况下,即使执行第二种正则,算法依旧会生成低质量的网络结构。
Experiments
Cell arch in different Search Stage
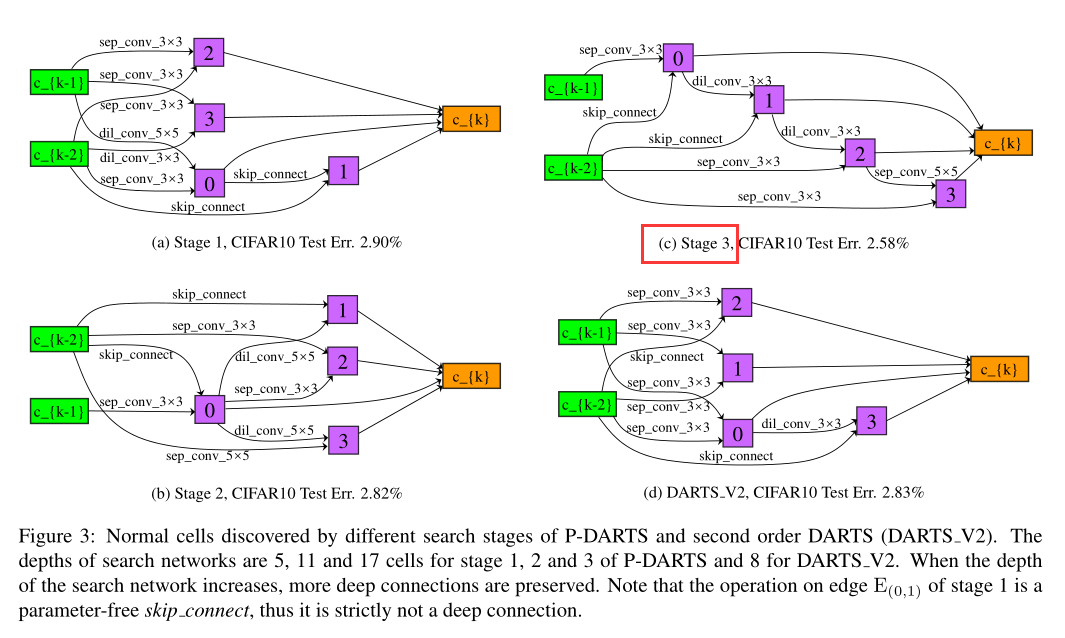
cifar10
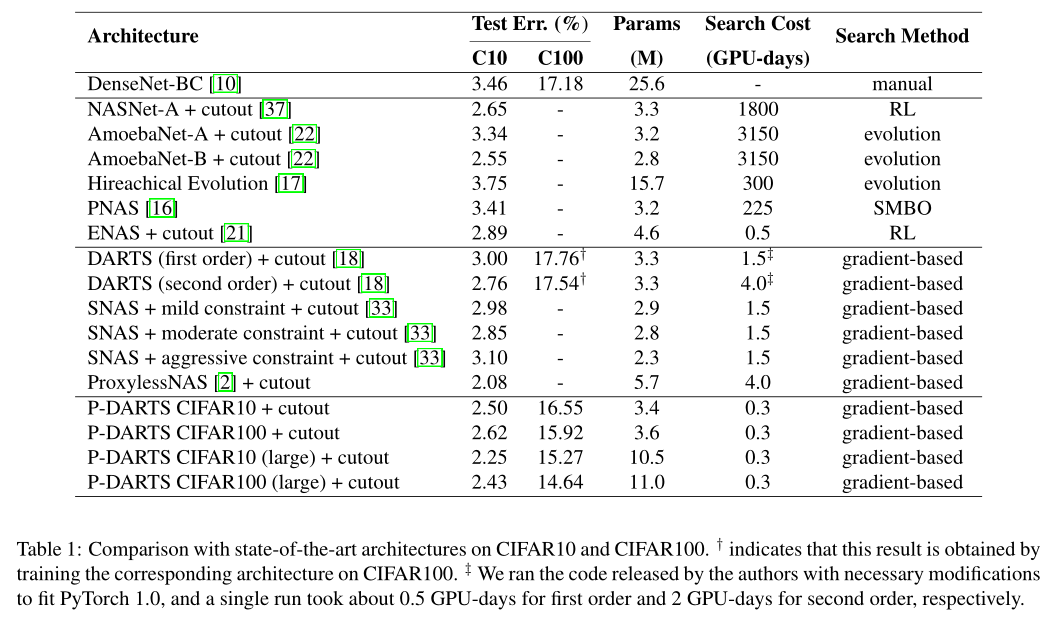
ImageNet
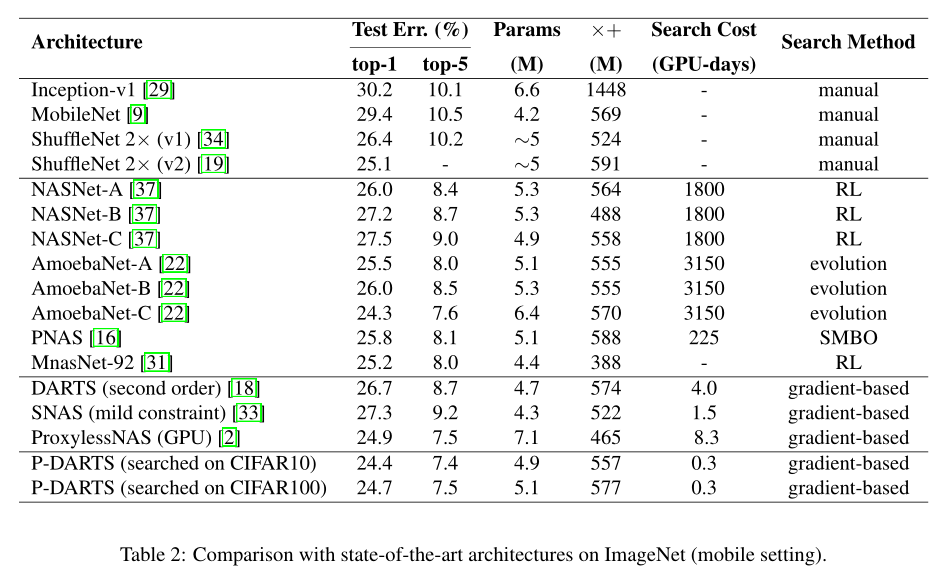 ·
·
Conclusion
-
we propose a progressive version of differentiable architecture search to bridge the depth gap between search and evaluation scenarios.
-
The core idea is to gradually increase the depth of candidate architectures during the search process.
-
2Q: computational overhead and instability
-
Search space approximate and Search space regularize
-
Our research defends the importance of depth in differentiable architecture search, depth is still the dominant factor in exploring the architecture space.
700. Search in a Binary Search Tree
700. Search in a Binary Search Tree
Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST that the node‘s value equals the given value. Return the subtree rooted with that node. If such node doesn‘t exist,you should return NULL.
For example,
Given the tree:
4
/ 2 7
/ 1 3
And the value to search: 2
You should return this subtree:
2
/ \
1 3
In the example above,if we want to search the value 5,since there is no node with value 5,we should return NULL.
Note that an empty tree is represented by NULL,therefore you would see the expected output (serialized tree format) as [],not null.
#include <cstdio> struct TreeNode{ int val; TreeNode* left; TreeNode* right; TreeNode(int x):val(x),left(NULL),right(NULL){} }; class Solution { public: TreeNode* searchBST(TreeNode* root,int val) { if(root==NULL||root->val==val){ return root; } if(val<root->val) return searchBST(root->left,val); else return searchBST(root->right,val); } };
今天关于NumPy-为二维数组排序的np.search和numpy 二维数组排序的分享就到这里,希望大家有所收获,若想了解更多关于"二分查找 (Binary Search)" 与 "斐波那契查找 (Fibonacci Search)"、/search 'search' 对象的 AttributeError 没有属性 'cleaned_data' django、2019-ICCV-Progressive Differentiable Architecture Search Bridging the Depth Gap Between Search an...、700. Search in a Binary Search Tree等相关知识,可以在本站进行查询。
本文标签:



![[转帖]Ubuntu 安装 Wine方法(ubuntu如何安装wine)](https://www.gvkun.com/zb_users/cache/thumbs/4c83df0e2303284d68480d1b1378581d-180-120-1.jpg)

