对于Python/numpy:捕获IEEE-754“inexact”异常感兴趣的读者,本文将提供您所需要的所有信息,我们将详细讲解python捕获错误,并且为您提供关于2021-05-27:定义何为s
对于Python / numpy:捕获IEEE-754“ inexact”异常感兴趣的读者,本文将提供您所需要的所有信息,我们将详细讲解python捕获错误,并且为您提供关于2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。、2021-05-27:定义何为step sum?比如680,680+68+6=754,680的step sum叫754。给定一个、754. Reach a Number、754. 到达终点数字 : 逐步剖析如何取得最小步数的宝贵知识。
本文目录一览:- Python / numpy:捕获IEEE-754“ inexact”异常(python捕获错误)
- 2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。
- 2021-05-27:定义何为step sum?比如680,680+68+6=754,680的step sum叫754。给定一个
- 754. Reach a Number
- 754. 到达终点数字 : 逐步剖析如何取得最小步数

Python / numpy:捕获IEEE-754“ inexact”异常(python捕获错误)
如何解决Python / numpy:捕获IEEE-754“ inexact”异常
numpy允许人们通过适当地使用IEEE-754 exceptions来处理源自浮点的np.seterr。但是seterr仅支持以下与IEEE-754异常相对应的关键字:
-
divide–除以零的处理。 -
under–处理浮点溢出。 -
over–处理浮点溢出。 -
invalid–处理无效的浮点运算。
但是,“ inexact” IEEE-754异常没有关键字。一个人怎么用Python处理呢?

2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。
2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。给定一个整数 num,判断它是不是某个数的 step sum?
福大大 答案 2021-05-27:
方法一:
自然智慧即可。二分法。在 0 到 num 之间找中点,然后求中点的 step sum。如果 step sum 太大,取左边;如果 step sum 太小,取右边。时间复杂度是 (log2N)*(log10N)。
方法二:
1. 求出不大于 num 的最大的全 1 数,然后 num / 全 1 数。如果商大于等于 10,直接返回 false。
2. 看余数。
2.1. 当余数不为 0 时,num = 余数,全 1 数 =(全 1 数 / 10),重复步骤 1。
2.2. 当余数为 0 时,返回 true。
时间复杂度是 log10N。
代码用 golang 编写。代码如下:
package main
import "fmt"
//05
func main() {
count := 0
for i := 1; i <= 11111; i++ {
ret1 := isStepSum1(i)
ret2 := isStepSum2(i)
fmt.Println(i, ret1, ret2)
count++
}
fmt.Println("正确数 = ", count)
}
//方法1
func isStepSum1(stepSum int) bool {
L := 0
R := stepSum
M := 0
cur := 0
for L <= R {
M = L + (R-L)>>1
cur = getStepSum(M)
if cur == stepSum {
return true
} else if cur < stepSum {
L = M + 1
} else {
R = M - 1
}
}
return false
}
func getStepSum(num int) int {
sum := 0
for num != 0 {
sum += num
num /= 10
}
return sum
}
//方法2
func isStepSum2(stepSum int) bool {
global111 := getGlobal111(stepSum)
for global111 > 0 {
quotient := stepSum / global111 //商
remainder := stepSum % global111 //余数
if quotient >= 10 {
return false
}
global111 /= 10
stepSum = remainder
}
return true
}
func getGlobal111(num int) int {
ans := 1
anstemp := 11
for anstemp <= num {
ans = anstemp
anstemp *= 10
anstemp++
}
return ans
}执行结果如下:
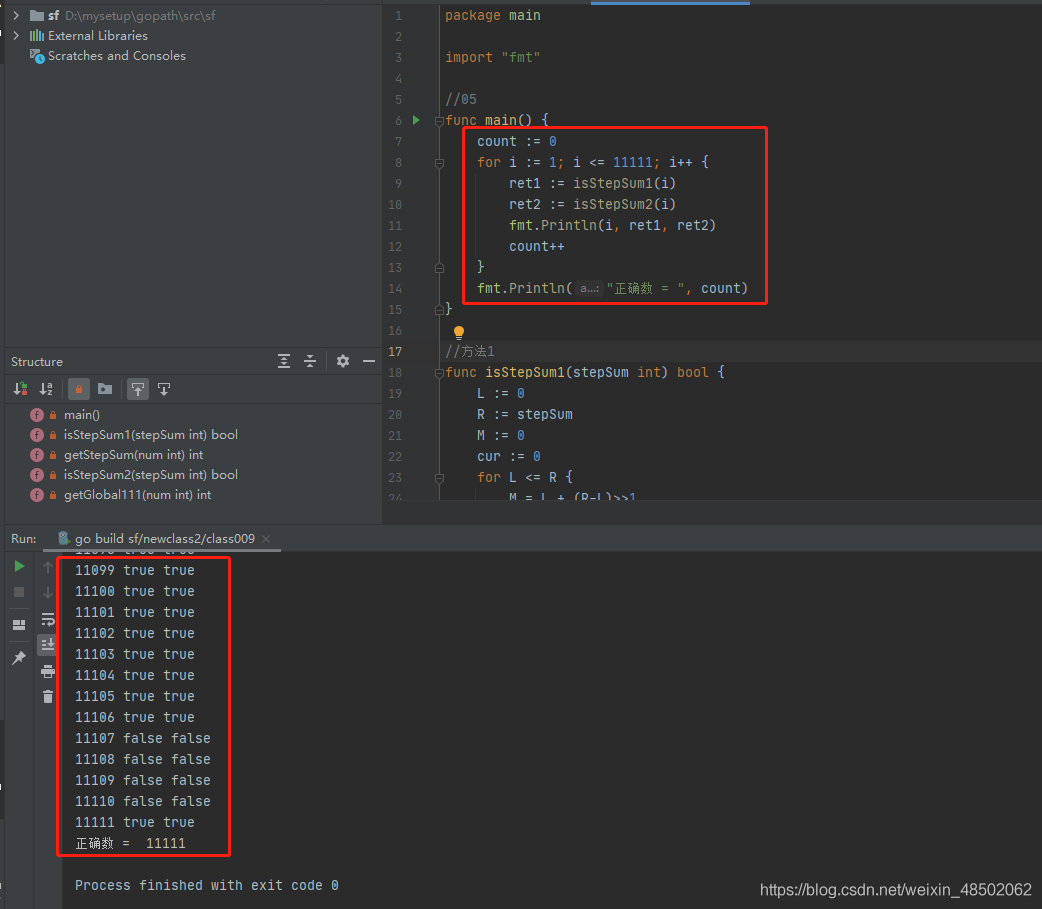
左神 java 代码

2021-05-27:定义何为step sum?比如680,680+68+6=754,680的step sum叫754。给定一个
2021-05-27:定义何为step sum?比如680,680+68+6=754,680的step sum叫754。给定一个整数num,判断它是不是某个数的step sum?
福大大 答案2021-05-27:
方法一:
自然智慧即可。二分法。在0到num之间找中点,然后求中点的step sum。如果step sum太大,取左边;如果step sum太小,取右边。时间复杂度是(log2N)*(log10N)。
方法二:
1.求出不大于num的最大的全1数,然后num/全1数。如果商大于等于10,直接返回false。
2.看余数。
2.1.当余数不为0时,num=余数,全1数=(全1数/10),重复步骤1。
2.2.当余数为0时,返回true。
时间复杂度是log10N。
代码用golang编写。代码如下:
package main
import "fmt"
//05func main() { count := 0 for i := 1; i <= 11111; i++ { ret1 := isStepSum1(i) ret2 := isStepSum2(i) fmt.Println(i, ret1, ret2) count++ } fmt.Println("正确数 = ", count)}
//方法1func isStepSum1(stepSum int) bool { L := 0 R := stepSum M := 0 cur := 0 for L <= R { M = L + (R-L)>>1 cur = getStepSum(M) if cur == stepSum { return true } else if cur < stepSum { L = M + 1 } else { R = M - 1 } } return false}
func getStepSum(num int) int { sum := 0 for num != 0 { sum += num num /= 10 } return sum}
//方法2func isStepSum2(stepSum int) bool { global111 := getGlobal111(stepSum) for global111 > 0 { quotient := stepSum / global111 //商 remainder := stepSum % global111 //余数 if quotient >= 10 { return false } global111 /= 10 stepSum = remainder } return true}
func getGlobal111(num int) int { ans := 1 anstemp := 11 for anstemp <= num { ans = anstemp anstemp *= 10 anstemp++ } return ans}
执行结果如下:
***
[左神java代码](https://gitee.com/moonfdd/coding-for-great-offer/blob/main/src/class09/Code05_IsStepSum.java)
本文分享自微信公众号 - 福大大架构师每日一题(gh_bbe96e5def84)。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。

754. Reach a Number
ou are standing at position 0 on an infinite number line. There is a goal at position target.
On each move, you can either go left or right. During the n-th move (starting from 1), you take n steps.
Return the minimum number of steps required to reach the destination.
Example 1:
Input: target = 3
Output: 2
Explanation:
On the first move we step from 0 to 1.
On the second step we step from 1 to 3.
Input: target = 2
Output: 3
Explanation:
On the first move we step from 0 to 1.
On the second move we step from 1 to -1.
On the third move we step from -1 to 2.找到达到目标点最小步数,第n步移动的距离为n,往左或往右都可以。
这是一个偶函数,走到target和-target都是一样的,所以只考虑target>0的情况。
1、如果能有n,使得sum = 1+2+...+n-1+n = target,显然,这是最佳方案。
2、如果sum > target,需要前面有反方向走的
2.1、delta = (sum - target) 是偶数,设第i,j...步往反方向走,那么最后到达的距离是: sum - 2*(i+j+...),其中i, j...∈[1, n],由于delta是偶数,必定存在i,j,...,使得2*(i+j+...) = delta。所以这种情况下,最佳步数还是n。
2.2、delta = (sum - target) 是奇数,这样2.1情况下的i, j...找不到,需要加步数。所以最后到达的距离是: sum - 2*(i+j+...) + n+1 + n+2 +...+ n+k ,现在需要找出最小的k。显然,k需要满足的条件是:使 sum + n+1 + n+2 +...+ n+k - delta 为偶数,即 n+1 + n+2 +...+ n+k 为奇数,这样就能找到符合条件的i,j,...。所以,当n是偶数时,n+1就是奇数,只需要加1步;否则,加2步。
class Solution {
public:
int reachNumber(int target) {
int n = 0;
int sum = 0;
target = abs(target);
while (sum<target) {
++n;
sum += n;
}
if ((sum-target)%2==0)
return n;
else {
if (n%2==0)
return n+1;
else
return n+2;
}
}
};

754. 到达终点数字 : 逐步剖析如何取得最小步数
题目描述
这是 LeetCode 上的 754. 到达终点数字 ,难度为 中等。
Tag : 「数学」
在一根无限长的数轴上,你站在 0 的位置。终点在 target 的位置。
你可以做一些数量的移动 numMoves :
- 每次你可以选择向左或向右移动。
- 第
i次移动(从i == 1开始,到i == numMoves),在选择的方向上走i步。
给定整数 target,返回 到达目标所需的 最小 移动次数(即最小 numMoves ) 。
示例 1:
输入: target = 2
输出: 3
解释:
第一次移动,从 0 到 1 。
第二次移动,从 1 到 -1 。
第三次移动,从 -1 到 2 。示例 2:
输入: target = 3
输出: 2
解释:
第一次移动,从 0 到 1 。
第二次移动,从 1 到 3 。提示:
- $-10^9 <= target <= 10^9$
- $target != 0$
数学
提示一:数轴上的任意点都以起点($0$ 点)对称,只需要考虑对称点的任意一边
由于题目没有限制我们「不能到达哪些点」以及「出发的起始方向」,因此以起点为中心的左右两边对称。
即:左边所能到达任意一个点,都能通过调整所达路径的方向来将终点调整到右边。
同时由于起点是一个特殊的位置 $0$ 点,因此相应的「正数点」和「负数点」对称,我们仅需考虑一边(例如正数域)即可。
提示二:先往靠近 target 的方向移动,到达或越过 target 的时候则停止
只考虑 target 为正的情况,我们假定起始先往靠近 target 的方向移动(即所有步数均为正值),根据是「到达」还是「越过」target 位置分情况讨论:
- 若能直接到达
target,此时消耗的必然是最小步数,可直接返回; - 若越过了
target,假设此时消耗的步数为 $k$,所走的距离为 $dist = \frac{k \times (k + 1)}{2} > target$,我们可以考虑是否需要增加额外步数来到达target。
提示三:越过 target 时,如何不引入额外步数
若不引入额外步数,意味着我们需要将此前某些移动的方向进行翻转,使得调整后的 $dist = target$。
我们假设需要调整的步数总和为 tot,则有 $dist - 2 \times tot = target$,变形可得 $tot = \frac{dist - target}{2}$。
若想满足上述性质,需要确保能找到这样的 tot,即 tot 合法,
不难推导出当 dist 和 target 差值为「偶数」时(两者奇偶性相同),我们可以找到这样的 tot,从而实现不引入额外步数来到达 target 位置。
由于我们的 $dist$ 是由数列 $[1,2,3,...,k]$ 累加而来,因此必然能够在该数列 $[1,2,3...k]$ 中通过「不重复选择某些数」来凑成任意一个小于等于 $dist$ 的数。
提示四:越过 target 时,如何尽量减少引入额外步数
当 dist 和 target 差值不为「偶数」时,我们只能通过引入额外步数(继续往右走)来使得,两者差值为偶数。
可以证明,最多引入步数不超过 $4$ 步,可使用得两者奇偶性相同,即不超过 $4$ 步可以覆盖到「奇数」和「偶数」两种情况。
根据 $k$ 与 $4$ 的余数关系分情况讨论:
- 余数为 $0$,即 $k = 4X$,由于 $dist = \frac{k(k+1)}{2} = \frac{4X(4X+1)}{2} = 2X(4X+1)$,其中一数为偶数,$dist$ 为偶数;
- 余数为 $1$,即 $k = 4X + 1$,由于 $dist = \frac{k(k+1)}{2} = \frac{(4X+1)(4X+2)}{2} = (4X+1)(2X+1)$,两个奇数相乘为奇数,$dist$ 为奇数;
- 余数为 $2$,即 $k = 4X + 2$,$dist = \frac{k(k+1)}{2} = \frac{(4X+2)(4X+3)}{2} = (2X+1)(4X+3)$,两个奇数相乘为奇数,$dist$ 为奇数;
- 余数为 $3$,即 $k = 4X + 3$,$dist = \frac{k(k+1)}{2} = \frac{(4X+3)(4X+4)}{2} = (4X+3)(2X+2)$,其中一数为偶数,$dist$ 为偶数。
因此在越过 target 后,最多引入不超过 $4$ 步可使得 dist 和 target 奇偶性相同。
提示五:如何不通过「遍历」或「二分」的方式找到一个合适的 k 值,再通过不超过 $4$ 步的调整找到答案
我们期望找到一个合适的 k 值,使得 $dist = \frac{k \times (k + 1)}{2} < target$,随后通过增加 k 值来找到答案。
利用求和公式 $dist = \frac{k \times (k + 1)}{2}$,我们可以设定 $k = \left \lfloor \sqrt{2 \times target}) \right \rfloor$ 为起始值,随后逐步增大 k 值,直到满足「dist 和 target 奇偶性相同」。
Java 代码:
class Solution {
public int reachNumber(int target) {
if (target < 0) target = -target;
int k = (int) Math.sqrt(2 * target), dist = k * (k + 1) / 2;
while (dist < target || (dist - target) % 2 == 1) {
k++;
dist = k * (k + 1) / 2;
}
return k;
}
}TypeScript 代码:
function reachNumber(target: number): number {
if (target < 0) target = -target
let k = Math.floor(Math.sqrt(2 * target)), dist = k * (k + 1) / 2
while (dist < target || (dist - target) % 2 == 1) {
k++
dist = k * (k + 1) / 2
}
return k
}Python 代码:
class Solution:
def reachNumber(self, target: int) -> int:
if target < 0:
target = -target
k = int(math.sqrt(2 * target))
dist = k * (k + 1) / 2
while dist < target or (dist - target) % 2 == 1:
k += 1
dist = k * (k + 1) / 2
return k- 时间复杂度:$O(1)$
- 空间复杂度:$O(1)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.754 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSou... 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地
本文由mdnice多平台发布
我们今天的关于Python / numpy:捕获IEEE-754“ inexact”异常和python捕获错误的分享就到这里,谢谢您的阅读,如果想了解更多关于2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。、2021-05-27:定义何为step sum?比如680,680+68+6=754,680的step sum叫754。给定一个、754. Reach a Number、754. 到达终点数字 : 逐步剖析如何取得最小步数的相关信息,可以在本站进行搜索。
本文标签:





