如果您想了解Pythonnumpy模块-ediff1d()实例源码的相关知识,那么本文是一篇不可错过的文章,我们将对python中numpy模块进行全面详尽的解释,并且为您提供关于Jupyter中的N
如果您想了解Python numpy 模块-ediff1d() 实例源码的相关知识,那么本文是一篇不可错过的文章,我们将对python中numpy模块进行全面详尽的解释,并且为您提供关于Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable、numpy.random.random & numpy.ndarray.astype & numpy.arange、numpy.ravel()/numpy.flatten()/numpy.squeeze()、Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性的有价值的信息。
本文目录一览:- Python numpy 模块-ediff1d() 实例源码(python中numpy模块)
- Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable
- numpy.random.random & numpy.ndarray.astype & numpy.arange
- numpy.ravel()/numpy.flatten()/numpy.squeeze()
- Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性

Python numpy 模块-ediff1d() 实例源码(python中numpy模块)
Python numpy 模块,ediff1d() 实例源码
我们从Python开源项目中,提取了以下20个代码示例,用于说明如何使用numpy.ediff1d()。
- def eta(radii, phot):
- """
- eta = I(r) / \\bar{I}(<r)
- radii -- 1d array of aperture photometry radii
- phot -- 1d array of aperture photometry fluxes
- this is currently calculated quite naively,and probably Could be done better
- """
- phot_area = np.pi * radii**2
- phot_area_diff = np.ediff1d(phot_area, to_begin=phot_area[0])
- I_bar = phot / (phot_area)
- I_delta_r = np.ediff1d(phot, to_begin=phot[0]) / phot_area_diff
- I_r = (I_delta_r[:-1] + I_delta_r[1:]) / 2 #lost last array element here
- I_r = np.append(I_r, I_delta_r[-1]) #added it back in here
- eta = I_r / I_bar
- return eta
- def SpaceFunc(val_x_array,val_y_array):
- spa_X_array = np.ediff1d(val_x_array)
- spa_Y_array = np.ediff1d(val_y_array)
- return spa_X_array,spa_Y_array
- #Fucntion to convert matrix to binary (those with value to 1,those with 0 to 0)
- def SpaceFunc(matr):
- matr_shape = matr.shape
- spa_X_array = np.array([])
- spa_Y_array = np.array([])
- val_X_matrix = np.zeros((matr_shape[0], matr_shape[1]), dtype=np.ndarray)
- val_Y_matrix = np.zeros((matr_shape[0], dtype=np.ndarray)
- val_X_matrix_counter = np.zeros((matr_shape[0], dtype=np.ndarray)
- val_Y_matrix_counter=np.zeros((matr_shape[0], dtype=np.ndarray)
- counter_g1 = 0
- while counter_g1 < matr_shape[1]:
- counter_g2 = 0
- while counter_g2 < matr_shape[0]:
- matr_value = matr[counter_g2, counter_g1]
- matr_value=np.asarray(matr_value)
- if matr_value.size==3:
- val_X_matrix[counter_g2, counter_g1] = matr_value[0]
- val_Y_matrix[counter_g2, counter_g1] = matr_value[1]
- val_X_matrix_counter[counter_g2, counter_g1] = 1
- val_Y_matrix_counter[counter_g2, counter_g1] = 1
- elif matr_value.size == 0:
- val_X_matrix[counter_g2, counter_g1] = 0
- val_Y_matrix[counter_g2, counter_g1] = 0
- val_X_matrix_counter[counter_g2, counter_g1] = 0
- val_Y_matrix_counter[counter_g2, counter_g1] = 0
- counter_g2 = counter_g2 + 1
- counter_g1 = counter_g1 + 1
- val_X_array_counter = val_X_matrix_counter.sum(axis=0)
- val_Y_array_counter = val_Y_matrix_counter.sum(axis=1)
- val_X_array_acc = val_X_matrix.sum(axis=0)
- val_Y_array_acc=val_Y_matrix.sum(axis=1)
- val_X_array = val_X_array_acc/val_X_array_counter
- val_Y_array = val_Y_array_acc / val_Y_array_counter
- spa_X_array=np.ediff1d(val_X_array)
- spa_Y_array=np.ediff1d(val_Y_array)
- #Creating function to convert matrix to binary (those with value to 1,those with 0 to 0)
- def SpaceFunc(matr):
- matr_shape = matr.shape
- spa_X_array = np.array([])
- spa_Y_array = np.array([])
- val_X_matrix = np.zeros((matr_shape[0],those with 0 to 0)
- def learning_rate(lr=LEARNING_RATE):
- decrease_rate = 0.75
- lr = lr
- window = []
- window_size = 5
- def f(loss = float(''inf'')):
- nonlocal window
- nonlocal lr
- nonlocal window_size
- window.append(loss)
- if len(window) == window_size:
- diffs = np.ediff1d(window)
- if np.all(abs(diffs) > np.array(window[:-1])*0.05) and np.mean(diffs > 0) >= 0.5: # if large loss
- # fluctuations
- print("fluctuating", window)
- lr *= decrease_rate
- window = []
- elif np.all(abs(diffs) < np.array(window[:-1])*0.01) and np.all(diffs < 0): # if decreased by
- # small amount
- print("too slow", window)
- lr *= 1/decrease_rate
- window = []
- else:
- window.pop(0)
- return lr
- return f
- def stopping_rule():
- window = []
- window_size = 5
- def c(val_acc):
- nonlocal window
- nonlocal window_size
- print(''acc'', val_acc)
- window.append(val_acc)
- if len(window) == window_size:
- diffs = np.ediff1d(window)
- if np.all(diffs < 0):
- return True
- window.pop(0)
- return False
- return c
- def ediff1d(ary, to_end=None, to_begin=None):
- """
- The differences between consecutive elements of an array.
- Parameters
- ----------
- ary : array_like
- If necessary,will be flattened before the differences are taken.
- to_end : array_like,optional
- Number(s) to append at the end of the returned differences.
- to_begin : array_like,optional
- Number(s) to prepend at the beginning of the returned differences.
- Returns
- -------
- ediff1d : ndarray
- The differences. Loosely,this is ``ary.flat[1:] - ary.flat[:-1]``.
- See Also
- --------
- diff,gradient
- Notes
- -----
- When applied to masked arrays,this function drops the mask information
- if the `to_begin` and/or `to_end` parameters are used.
- Examples
- --------
- >>> x = np.array([1,2,4,7,0])
- >>> np.ediff1d(x)
- array([ 1,3,-7])
- >>> np.ediff1d(x,to_begin=-99,to_end=np.array([88,99]))
- array([-99,1,-7,88,99])
- The returned array is always 1D.
- >>> y = [[1,4],[1,6,24]]
- >>> np.ediff1d(y)
- array([ 1,-3,5,18])
- """
- ary = np.asanyarray(ary).flat
- ed = ary[1:] - ary[:-1]
- arrays = [ed]
- if to_begin is not None:
- arrays.insert(0, to_begin)
- if to_end is not None:
- arrays.append(to_end)
- if len(arrays) != 1:
- # We''ll save ourselves a copy of a potentially large array in
- # the common case where neither to_begin or to_end was given.
- ed = np.hstack(arrays)
- return ed
- def setxor1d(ar1, ar2, assume_unique=False):
- """
- Find the set exclusive-or of two arrays.
- Return the sorted,unique values that are in only one (not both) of the
- input arrays.
- Parameters
- ----------
- ar1,ar2 : array_like
- Input arrays.
- assume_unique : bool
- If True,the input arrays are both assumed to be unique,which
- can speed up the calculation. Default is False.
- Returns
- -------
- setxor1d : ndarray
- Sorted 1D array of unique values that are in only one of the input
- arrays.
- Examples
- --------
- >>> a = np.array([1,4])
- >>> b = np.array([2,5])
- >>> np.setxor1d(a,b)
- array([1,7])
- """
- if not assume_unique:
- ar1 = unique(ar1)
- ar2 = unique(ar2)
- aux = np.concatenate((ar1, ar2))
- if aux.size == 0:
- return aux
- aux.sort()
- # flag = ediff1d( aux,to_end = 1,to_begin = 1 ) == 0
- flag = np.concatenate(([True], aux[1:] != aux[:-1], [True]))
- # flag2 = ediff1d( flag ) == 0
- flag2 = flag[1:] == flag[:-1]
- return aux[flag2]
- def _compute_snp_distances(self, df, build):
- if build == 36:
- hapmap = self._resources.get_hapmap_h36()
- else:
- hapmap = self._resources.get_hapmap_h37()
- for chrom in df[''chrom''].unique():
- if chrom not in hapmap.keys():
- continue
- # create a new dataframe from the positions for the current chromosome
- temp = pd.DataFrame(df.loc[(df[''chrom''] == chrom)][''pos''].values, columns=[''pos''])
- # merge HapMap for this chrom
- temp = temp.append(hapmap[chrom], ignore_index=True)
- # sort based on pos
- temp = temp.sort_values(''pos'')
- # fill cM rates forward and backward
- temp[''rate''] = temp[''rate''].fillna(method=''ffill'')
- temp[''rate''] = temp[''rate''].fillna(method=''bfill'')
- # get difference between positions
- pos_diffs = np.ediff1d(temp[''pos''])
- # compute cMs between each pos based on probabilistic recombination rate
- # https://www.biostars.org/p/123539/
- cMs_match_segment = (temp[''rate''] * np.r_[pos_diffs, 0] / 1e6).values
- # add back into temp
- temp[''cMs''] = np.r_[0, cMs_match_segment][:-1]
- temp = temp.reset_index()
- del temp[''index'']
- # use null `map` values to find locations of SNPs
- snp_indices = temp.loc[temp[''map''].isnull()].index
- # use SNP indices to determine boundaries over which to sum cMs
- start_snp_ix = snp_indices + 1
- end_snp_ix = np.r_[snp_indices, snp_indices[-1]][1:] + 1
- snp_boundaries = np.c_[start_snp_ix, end_snp_ix]
- # sum cMs between SNPs to get total cM distance between SNPs
- # http://stackoverflow.com/a/7471967
- c = np.r_[0, temp[''cMs''].cumsum()][snp_boundaries]
- cM_from_prev_snp = c[:, 1] - c[:, 0]
- # debug
- # temp.loc[snp_indices,''cM_from_prev_snp''] = np.r_[0,cM_from_prev_snp][:-1]
- # temp.to_csv(''debug.csv'')
- # add back into df
- df.loc[(df[''chrom''] == chrom), ''cM_from_prev_snp''] = np.r_[0, cM_from_prev_snp][:-1]
- return hapmap, df
- def ediff1d(ary, to_begin)
- if to_end is not None:
- arrays.append(to_end)
- if len(arrays) != 1:
- # We''ll save ourselves a copy of a potentially large array in
- # the common case where neither to_begin or to_end was given.
- ed = np.hstack(arrays)
- return ed
- def setxor1d(ar1, [True]))
- # flag2 = ediff1d( flag ) == 0
- flag2 = flag[1:] == flag[:-1]
- return aux[flag2]
- def ediff1d(ary, to_begin)
- if to_end is not None:
- arrays.append(to_end)
- if len(arrays) != 1:
- # We''ll save ourselves a copy of a potentially large array in
- # the common case where neither to_begin or to_end was given.
- ed = np.hstack(arrays)
- return ed
- def setxor1d(ar1, [True]))
- # flag2 = ediff1d( flag ) == 0
- flag2 = flag[1:] == flag[:-1]
- return aux[flag2]
- def estimate_baresine(self, x_axis, data, params):
- """ Bare sine estimator with a frequency and phase.
- @param numpy.array x_axis: 1D axis values
- @param numpy.array data: 1D data,should have the same dimension as x_axis.
- @param lmfit.Parameters params: object includes parameter dictionary which
- can be set
- @return tuple (error,params):
- Explanation of the return parameter:
- int error: error code (0:OK,-1:error)
- lmfit.Parameters params: derived OrderedDict object contains the initial
- values for the fit.
- """
- # Convert for safety:
- x_axis = np.array(x_axis)
- data = np.array(data)
- error = self._check_1D_input(x_axis=x_axis, data=data, params=params)
- # calculate dft with zeropadding to obtain nicer interpolation between the
- # appearing peaks.
- dft_x, dft_y = compute_ft(x_axis, zeropad_num=1)
- stepsize = x_axis[1]-x_axis[0] # for frequency axis
- frequency_max = np.abs(dft_x[np.log(dft_y).argmax()])
- # find minimal distance to the next meas point in the corresponding time value>
- min_x_diff = np.ediff1d(x_axis).min()
- # How many points are used to sample the estimated frequency with min_x_diff:
- iter_steps = int(1/(frequency_max*min_x_diff))
- if iter_steps < 1:
- iter_steps = 1
- sum_res = np.zeros(iter_steps)
- # Procedure: Create sin waves with different phases and perform a summation.
- # The sum shows how well the sine was fitting to the actual data.
- # The best fitting sine should be a maximum of the summed time
- # trace.
- for iter_s in range(iter_steps):
- func_val = np.sin(2*np.pi*frequency_max*x_axis + iter_s/iter_steps *2*np.pi)
- sum_res[iter_s] = np.abs(data - func_val).sum()
- # The minimum indicates where the sine function was fittng the worst,
- # therefore subtract pi. This will also ensure that the estimated phase will
- # be in the interval [-pi,pi].
- phase = sum_res.argmax()/iter_steps *2*np.pi - np.pi
- params[''frequency''].set(value=frequency_max, min=0.0, max=1/(stepsize)*3)
- params[''phase''].set(value=phase, min=-np.pi, max=np.pi)
- return error, params
- def sine_testing2():
- """ Sinus fit testing with the direct fit method. """
- x_axis = np.linspace(0, 250, 75)
- x_axis1 = np.linspace(250, 500, 75)
- x_axis = np.append(x_axis, x_axis1)
- x_nice = np.linspace(x_axis[0],x_axis[-1], 1000)
- mod, params = qudi_fitting.make_sine_model()
- params[''phase''].value = np.pi/2 # np.random.uniform()*2*np.pi
- params[''frequency''].value = 0.01
- params[''amplitude''].value = 1.5
- params[''offset''].value = 0.4
- data = mod.eval(x=x_axis, params=params)
- data_noisy = (mod.eval(x=x_axis, params=params)
- + 1.5* np.random.normal(size=x_axis.shape))
- # sorted_indices = x_axis.argsort()
- # x_axis = x_axis[sorted_indices]
- # data = data[sorted_indices]
- # diff_array = np.ediff1d(x_axis)
- # print(diff_array)
- # print(diff_array.min())
- # min_x_diff = diff_array.min()
- # if np.isclose(min_x_diff,0.0):
- # index = np.argmin(diff_array)
- # print(''index'',index)
- # diff_array = np.delete(diff_array,index)
- # print(''diff_array'',diff_array)
- update_dict = {}
- update_dict[''phase''] = {''vary'': False, ''value'': np.pi/2.}
- result = qudi_fitting.make_sine_fit(x_axis=x_axis, data=data_noisy,
- add_params=update_dict)
- plt.figure()
- # plt.plot(x_axis,data,''simulate data'')
- plt.plot(x_axis, data_noisy, label=''noisy data'')
- plt.plot(x_axis, result.init_fit, label=''initial data'')
- plt.plot(x_axis, result.best_fit, label=''fit data'')
- plt.xlabel(''time'')
- plt.ylabel(''signal'')
- plt.legend(bBox_to_anchor=(0., 1.02, 1., .102), loc=3,
- ncol=2, mode="expand", borderaxespad=0.)
- plt.show()
- def ediff1d(ary, to_begin)
- if to_end is not None:
- arrays.append(to_end)
- if len(arrays) != 1:
- # We''ll save ourselves a copy of a potentially large array in
- # the common case where neither to_begin or to_end was given.
- ed = np.hstack(arrays)
- return ed
- def setxor1d(ar1, [True]))
- # flag2 = ediff1d( flag ) == 0
- flag2 = flag[1:] == flag[:-1]
- return aux[flag2]
- def setxor1d(ar1, [True]))
- # flag2 = ediff1d( flag ) == 0
- flag2 = flag[1:] == flag[:-1]
- return aux[flag2]
- def ediff1d(ary, to_begin)
- if to_end is not None:
- arrays.append(to_end)
- if len(arrays) != 1:
- # We''ll save ourselves a copy of a potentially large array in
- # the common case where neither to_begin or to_end was given.
- ed = np.hstack(arrays)
- return ed
- def setxor1d(ar1, [True]))
- # flag2 = ediff1d( flag ) == 0
- flag2 = flag[1:] == flag[:-1]
- return aux[flag2]

Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable
如何解决Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: ''numpy.ndarray'' object is not callable?
晚安, 尝试打印以下内容时,我在 jupyter 中遇到了 numpy 问题,并且得到了一个 错误: 需要注意的是python版本是3.8.8。 我先用 spyder 测试它,它运行正确,它给了我预期的结果
使用 Spyder:
import numpy as np
for i in range (5):
n = np.random.rand ()
print (n)
Results
0.6604903457995978
0.8236300859753154
0.16067650689842816
0.6967868357083673
0.4231597934445466
现在有了 jupyter
import numpy as np
for i in range (5):
n = np.random.rand ()
print (n)
-------------------------------------------------- ------
TypeError Traceback (most recent call last)
<ipython-input-78-0c6a801b3ea9> in <module>
2 for i in range (5):
3 n = np.random.rand ()
----> 4 print (n)
TypeError: ''numpy.ndarray'' object is not callable
感谢您对我如何在 Jupyter 中解决此问题的帮助。
非常感谢您抽出宝贵时间。
阿特,约翰”
解决方法
暂无找到可以解决该程序问题的有效方法,小编努力寻找整理中!
如果你已经找到好的解决方法,欢迎将解决方案带上本链接一起发送给小编。
小编邮箱:dio#foxmail.com (将#修改为@)

numpy.random.random & numpy.ndarray.astype & numpy.arange
今天看到这样一句代码:
xb = np.random.random((nb, d)).astype(''float32'') #创建一个二维随机数矩阵(nb行d列)
xb[:, 0] += np.arange(nb) / 1000. #将矩阵第一列的每个数加上一个值要理解这两句代码需要理解三个函数
1、生成随机数
numpy.random.random(size=None)
size为None时,返回float。
size不为None时,返回numpy.ndarray。例如numpy.random.random((1,2)),返回1行2列的numpy数组
2、对numpy数组中每一个元素进行类型转换
numpy.ndarray.astype(dtype)
返回numpy.ndarray。例如 numpy.array([1, 2, 2.5]).astype(int),返回numpy数组 [1, 2, 2]
3、获取等差数列
numpy.arange([start,]stop,[step,]dtype=None)
功能类似python中自带的range()和numpy中的numpy.linspace
返回numpy数组。例如numpy.arange(3),返回numpy数组[0, 1, 2]

numpy.ravel()/numpy.flatten()/numpy.squeeze()
numpy.ravel(a, order=''C'')
Return a flattened array
numpy.chararray.flatten(order=''C'')
Return a copy of the array collapsed into one dimension
numpy.squeeze(a, axis=None)
Remove single-dimensional entries from the shape of an array.
相同点: 将多维数组 降为 一维数组
不同点:
ravel() 返回的是视图(view),意味着改变元素的值会影响原始数组元素的值;
flatten() 返回的是拷贝,意味着改变元素的值不会影响原始数组;
squeeze()返回的是视图(view),仅仅是将shape中dimension为1的维度去掉;
ravel()示例:
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.ravel()
16 print("a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19
20 print(a)
21 log_type(''a'',a)
flatten()示例
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.flatten()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)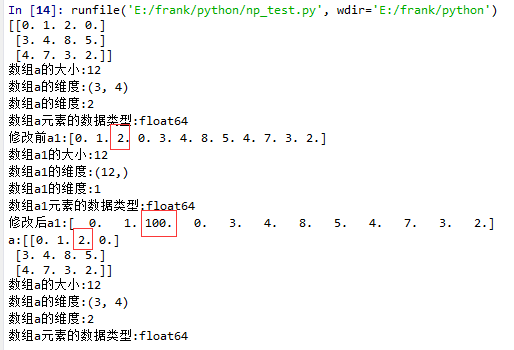
squeeze()示例:
1. 没有single-dimensional entries的情况
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.squeeze()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)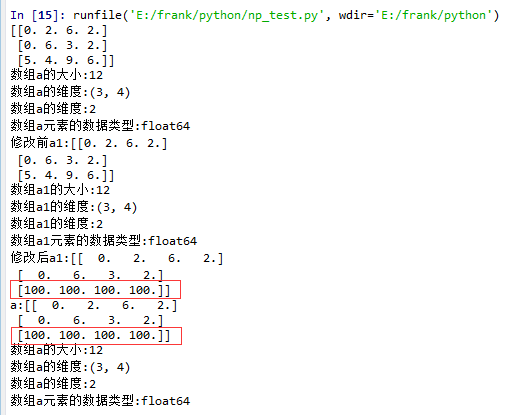
从结果中可以看到,当没有single-dimensional entries时,squeeze()返回额数组对象是一个view,而不是copy。
2. 有single-dimentional entries 的情况
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((1,3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.squeeze()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)

Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性
一、Numpy数组创建
part 1:np.linspace(起始值,终止值,元素总个数
import numpy as np
''''''
numpy中的ndarray数组
''''''
ary = np.array([1, 2, 3, 4, 5])
print(ary)
ary = ary * 10
print(ary)
''''''
ndarray对象的创建
''''''
# 创建二维数组
# np.array([[],[],...])
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(a)
# np.arange(起始值, 结束值, 步长(默认1))
b = np.arange(1, 10, 1)
print(b)
print("-------------np.zeros(数组元素个数, dtype=''数组元素类型'')-----")
# 创建一维数组:
c = np.zeros(10)
print(c, ''; c.dtype:'', c.dtype)
# 创建二维数组:
print(np.zeros ((3,4)))
print("----------np.ones(数组元素个数, dtype=''数组元素类型'')--------")
# 创建一维数组:
d = np.ones(10, dtype=''int64'')
print(d, ''; d.dtype:'', d.dtype)
# 创建三维数组:
print(np.ones( (2,3,4), dtype=np.int32 ))
# 打印维度
print(np.ones( (2,3,4), dtype=np.int32 ).ndim) # 返回:3(维)
结果图:

part 2 :np.linspace ( 起始值,终止值,元素总个数)
import numpy as np
a = np.arange( 10, 30, 5 )
b = np.arange( 0, 2, 0.3 )
c = np.arange(12).reshape(4,3)
d = np.random.random((2,3)) # 取-1到1之间的随机数,要求设置为诶2行3列的结构
print(a)
print(b)
print(c)
print(d)
print("-----------------")
from numpy import pi
print(np.linspace( 0, 2*pi, 100 ))
print("-------------np.linspace(起始值,终止值,元素总个数)------------------")
print(np.sin(np.linspace( 0, 2*pi, 100 )))
结果图:

二、Numpy的ndarray对象属性:
数组的结构:array.shape
数组的维度:array.ndim
元素的类型:array.dtype
数组元素的个数:array.size
数组的索引(下标):array[0]
''''''
数组的基本属性
''''''
import numpy as np
print("--------------------案例1:------------------------------")
a = np.arange(15).reshape(3, 5)
print(a)
print(a.shape) # 打印数组结构
print(len(a)) # 打印有多少行
print(a.ndim) # 打印维度
print(a.dtype) # 打印a数组内的元素的数据类型
# print(a.dtype.name)
print(a.size) # 打印数组的总元素个数
print("-------------------案例2:---------------------------")
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a)
# 测试数组的基本属性
print(''a.shape:'', a.shape)
print(''a.size:'', a.size)
print(''len(a):'', len(a))
# a.shape = (6, ) # 此格式可将原数组结构变成1行6列的数据结构
# print(a, ''a.shape:'', a.shape)
# 数组元素的索引
ary = np.arange(1, 28)
ary.shape = (3, 3, 3) # 创建三维数组
print("ary.shape:",ary.shape,"\n",ary )
print("-----------------")
print(''ary[0]:'', ary[0])
print(''ary[0][0]:'', ary[0][0])
print(''ary[0][0][0]:'', ary[0][0][0])
print(''ary[0,0,0]:'', ary[0, 0, 0])
print("-----------------")
# 遍历三维数组:遍历出数组里的每个元素
for i in range(ary.shape[0]):
for j in range(ary.shape[1]):
for k in range(ary.shape[2]):
print(ary[i, j, k], end='' '')
结果图:

我们今天的关于Python numpy 模块-ediff1d() 实例源码和python中numpy模块的分享就到这里,谢谢您的阅读,如果想了解更多关于Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable、numpy.random.random & numpy.ndarray.astype & numpy.arange、numpy.ravel()/numpy.flatten()/numpy.squeeze()、Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性的相关信息,可以在本站进行搜索。
本文标签:





