这篇文章主要围绕Pythonnumpy模块-iscomplex()实例源码和python中numpy模块展开,旨在为您提供一份详细的参考资料。我们将全面介绍Pythonnumpy模块-iscomple
这篇文章主要围绕Python numpy 模块-iscomplex() 实例源码和python中numpy模块展开,旨在为您提供一份详细的参考资料。我们将全面介绍Python numpy 模块-iscomplex() 实例源码的优缺点,解答python中numpy模块的相关问题,同时也会为您带来Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable、numpy.random.random & numpy.ndarray.astype & numpy.arange、numpy.ravel()/numpy.flatten()/numpy.squeeze()、Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性的实用方法。
本文目录一览:- Python numpy 模块-iscomplex() 实例源码(python中numpy模块)
- Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable
- numpy.random.random & numpy.ndarray.astype & numpy.arange
- numpy.ravel()/numpy.flatten()/numpy.squeeze()
- Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性

Python numpy 模块-iscomplex() 实例源码(python中numpy模块)
Python numpy 模块,iscomplex() 实例源码
我们从Python开源项目中,提取了以下11个代码示例,用于说明如何使用numpy.iscomplex()。
- def spectrum(x,
- n0=0,
- T_s=1,
- oversample=1,
- only_positive=True):
- """
- Return the spectrum for the signal *x* calculated via FFT and the
- associated frequencies as a tuple. The *n0* parameter gives the
- index in *x* for time index 0 (*n0* = 0 means that `x[0]` is at
- time 0). The number of spectral samples returned is the next power
- of 2 greater than the length of *x* multiplied by *oversample*. If
- *only_positive*,return the spectrum only for positive frequencies
- (and raise an exception if *x* is not real).
- """
- assert oversample >= 1 and isinstance(oversample, int)
- N = nextpow2(len(x)) * 2**(oversample - 1)
- X = NP.fft.fft(x, n=N) * T_s
- f = NP.fft.fftfreq(N, d=T_s)
- if n0 != 0:
- X *= NP.exp(-1j * 2 * math.pi * NP.arange(N) * n0 / N)
- X = NP.fft.fftshift(X)
- f = NP.fft.fftshift(f)
- if only_positive:
- if any(NP.iscomplex(x)):
- raise ValueError(''x is complex and only returning information for positive frequencies --- this is likely not what you want to do'')
- X = X[f >= 0]
- f = f[f >= 0]
- return X, f
- def plot_data(data, scroll_axis=2):
- """ Plot an image associated data.
- Currently support on 1D,2D or 3D data.
- Parameters
- ----------
- data: array
- the data to be displayed.
- scroll_axis: int (optional,default 2)
- the scroll axis for 3d data.
- """
- # Check input parameters
- if data.ndim not in range(1, 4):
- raise ValueError("Unsupported data dimension.")
- # Deal with complex data
- if numpy.iscomplex(data).any():
- data = numpy.abs(data)
- # Create application
- app = pyqtgraph.mkQApp()
- # Create the widget
- if data.ndim == 3:
- indices = [i for i in range(3) if i != scroll_axis]
- indices = [scroll_axis] + indices
- widget = pyqtgraph.image(numpy.transpose(data, indices))
- elif data.ndim == 2:
- widget = pyqtgraph.image(data)
- else:
- widget = pyqtgraph.plot(data)
- # Run application
- app.exec_()
- def average_structure(X):
- """
- Calculate an average structure from an ensemble of structures
- (i.e. X is a rank-3 tensor: X[i] is a (N,3) configuration matrix).
- @param X: m x n x 3 input vector
- @type X: numpy array
- @return: average structure
- @rtype: (n,3) numpy.array
- """
- from numpy.linalg import eigh
- B = csb.numeric.gower_matrix(X)
- v, U = eigh(B)
- if numpy.iscomplex(v).any():
- v = v.real
- if numpy.iscomplex(U).any():
- U = U.real
- indices = numpy.argsort(v)[-3:]
- v = numpy.take(v, indices, 0)
- U = numpy.take(U, 1)
- x = U * numpy.sqrt(v)
- i = 0
- while is_mirror_image(x, X[0]) and i < 2:
- x[:, i] *= -1
- i += 1
- return x
- def rel_entropy_true(p, q):
- """KL divergence (relative entropy) D(p||q) in bits
- Returns a scalar entropy when the input distributions p and q are
- vectors of probability masses,or returns in a row vector the
- columnwise relative entropies of the input probability matrices p and
- q"""
- if type(p) == list or type(q) == tuple:
- p = np.array(p)
- if type(q) == list or type(q) == tuple:
- q = np.array(q)
- if not p.shape == q.shape:
- raise Exception(''p and q must be equal sizes'',
- ''p: '' + str(p.shape),
- ''q: '' + str(q.shape))
- if (np.iscomplex(p).any() or not
- np.isfinite(p).any() or
- (p < 0).any() or
- (p > 1).any()):
- raise Exception(''The probability elements of p must be real numbers''
- ''between 0 and 1.'')
- if (np.iscomplex(q).any() or not
- np.isfinite(q).any() or
- (q < 0).any() or
- (q > 1).any()):
- raise Exception(''The probability elements of q must be real numbers''
- ''between 0 and 1.'')
- eps = math.sqrt(np.spacing(1))
- if (np.abs(np.sum(p, axis=0) - 1) > eps).any():
- raise Exception(''Sum of the probability elements of p must equal 1.'')
- if (np.abs(np.sum(q, axis=0) - 1) > eps).any():
- raise Exception(''Sum of the probability elements of q must equal 1.'')
- return sum(np.log2((p**p) / (q**p)))
- def pnorm(self, p):
- r"""
- Calculates the p-norm of a vector.
- Parameters
- ----------
- p : int
- Used in computing the p-norm. This should only be set
- when calculating the pnorm of a vector is desired.
- Returns
- -------
- pn : float
- The p-norm of the vector.
- Notes
- -----
- The p-norm,which is considered a class of vector norms is defined as:
- .. math::
- ||x||_p = \\sqrt[p]{|x_1|^p + |x_2|^p + \\cdots + |x_n|^p} \\qquad p \\geq 1
- References
- ----------
- Golub,G.,& Van Loan,C. (2013). Matrix computations (3rd ed.). Baltimore (MD): Johns Hopkins U.P.
- """
- if p != np.floor(p):
- p = np.floor(p)
- if np.iscomplex(p) or p < 1:
- raise ValueError(''p must be at least 1 and real'')
- pn = np.sum(np.absolute(self.x) ** p) ** (1. / p)
- return pn
- def __str__(self):
- # create local dictionary to convert node-numbers to node-labels
- num2node_label = {num: name for name, num in self.node_label2num.items()}
- # build message to print
- msg = ''------------------------\\n''
- msg += '' SpicePy.Network:\\n''
- msg += ''------------------------\\n''
- for ele, nodes, val in zip(self.names, self.nodes, self.values):
- # if val is a list --> ele is a transient source
- if isinstance(val, list):
- if self.source_type[ele] == ''pwl'':
- fmt = "{} {} {} {}(" + "{} " * (len(val[0]) - 1) + "{})\\n"
- msg += fmt.format(ele, num2node_label[nodes[0]], num2node_label[nodes[1]], self.source_type[ele], *val[0])
- else:
- fmt = "{} {} {} {}(" + "{} " * (len(val) - 1) + "{})\\n"
- msg += fmt.format(ele, *val)
- # if val is complex --> ele is a phasor
- elif np.iscomplex(val):
- msg += "{} {} {} {} {}\\n".format(ele, np.abs(val), np.angle(val) * 180/np.pi)
- # if ele is C or L
- elif ele[0].upper() == ''C'' or ele[0].upper() == ''L'':
- # check if an i.c. is present and print it
- if ele in self.IC:
- msg += "{} {} {} {} ic={}\\n".format(ele, val, self.IC[ele])
- # otherwise...
- else:
- msg += "{} {} {} {}\\n".format(ele, val)
- # otherwise...general case --> ele n+ n- val
- else:
- msg += "{} {} {} {}\\n".format(ele, val)
- # add analysis
- msg += " ".join(self.analysis) + ''\\n''
- # if a plot command is present,add it
- if self.plot_cmd is not None:
- msg += self.plot_cmd + ''\\n''
- # add number of nodes (reference node is included) and number of branches
- msg += ''------------------------\\n''
- msg += ''* number of nodes {}\\n''.format(self.node_num + 1)
- msg += ''* number of branches {}\\n''.format(len(self.names))
- msg += ''------------------------\\n''
- return msg
- def find_zero_crossing_quadratic(x1, y1, x2, y2, x3, y3, eps = 1.0):
- """ Find zero crossing using quadratic approximation along 1d line"""
- # compute coords along 1d line
- v = x2 - x1
- v = v / np.linalg.norm(v)
- if v[v!=0].shape[0] == 0:
- logging.error(''Difference is 0. Probably a bug'')
- t1 = 0
- t2 = (x2 - x1)[v!=0] / v[v!=0]
- t2 = t2[0]
- t3 = (x3 - x1)[v!=0] / v[v!=0]
- t3 = t3[0]
- # solve for quad approx
- x1_row = np.array([t1**2, t1, 1])
- x2_row = np.array([t2**2, t2, 1])
- x3_row = np.array([t3**2, t3, 1])
- X = np.array([x1_row, x2_row, x3_row])
- y_vec = np.array([y1, y3])
- try:
- w = np.linalg.solve(X, y_vec)
- except np.linalg.LinAlgError:
- logging.error(''Singular matrix. Probably a bug'')
- return None
- # get positive roots
- possible_t = np.roots(w)
- t_zc = None
- for i in range(possible_t.shape[0]):
- if possible_t[i] >= 0 and possible_t[i] <= 10 and not np.iscomplex(possible_t[i]):
- t_zc = possible_t[i]
- # if no positive roots find min
- if np.abs(w[0]) < 1e-10:
- return None
- if t_zc is None:
- t_zc = -w[1] / (2 * w[0])
- if t_zc < -eps or t_zc > eps:
- return None
- x_zc = x1 + t_zc * v
- return x_zc
- def run(X,y1,y2,dmax=None):
- D,N = X.shape
- y1_unique,J1 = np.unique(y1, return_inverse=True)
- ny1 = y1_unique.size
- y2_unique,J2 = np.unique(y2, return_inverse=True)
- ny2 = y2_unique.size
- Y1 = np.zeros((ny1,N))
- Y2 = np.zeros((ny2,N))
- Y1[J1,range(N)] = 1.
- Y2[J2,range(N)] = 1.
- XY2 = np.dot(X,Y2.T) # D x ny2
- XY2Y2X = np.dot(XY2,XY2.T) # D x D
- XX = np.dot(X,X.T) # D x D
- P = np.zeros((D,0))
- Sj = np.dot(X,Y1.T) # D x ny1
- if dmax==None:
- dmax = D
- for d in range(dmax):
- if d>0:
- invPP = np.linalg.pinv(np.dot(P.T,P))
- Sj -= np.dot(np.dot(np.dot(P,invPP),P.T),Sj)
- C = np.dot(Sj,Sj.T) - XY2Y2X
- C = 0.5*(C+C.T)
- dd,E = scipy.linalg.eigh(C,eigvals=(D-1,D-1)) # ascending order
- assert np.isnan(dd).any()==False
- assert np.iscomplex(dd).any()==False
- #dd = dd[::-1] #
- #E = E[:,::-1]
- wj = E#E[:,0] # D x 1
- pj = np.dot(XX,wj) / np.dot(np.dot(wj.T,XX),wj) # D x 1
- P = np.hstack((P,pj.reshape((D,1)))) # D x d
- #P = P/np.tile(np.sqrt((P**2).sum(axis=0,keepdims=True)),(D,1))
- #% They need not be orthogonal.
- return P
- def run(X,y2):
- # function [E,dd] = privacyLDA(X,y1,y2)
- # %max_W0 tr(W0''*C1*W0) - tr(W0''*C2*W0)
- D,N = X.shape
- y1_unique = np.unique(y1)
- #print y1_unique
- #[y1_unique,~,J1] = unique(y1);
- #ny1 = y1_unique.size
- y2_unique = np.unique(y2)
- #print y2_unique
- #[y2_unique,J2] = unique(y2);
- #ny2 = y2_unique.size
- C1 = np.zeros((D,D))
- C2 = np.zeros((D,D))
- mu = X.mean(axis=1).reshape((D,1))
- #print mu.shape
- for k in np.nditer(y1_unique):
- indk = np.where(y1==k)[0]
- muk = X[:,indk].mean(axis=1).reshape((D,1))
- #muk -= np.kron(np.ones((1,len(indk))),mu)
- #%C1 = C1 + ny1*(muk-mu)*(muk-mu)'';
- C1 = C1 + len(indk)*np.dot(muk-mu,(muk-mu).T)
- for k in np.nditer(y2_unique):
- indk = np.where(y2==k)[0]
- muk = X[:,mu)
- #%C1 = C1 + ny1*(muk-mu)*(muk-mu)'';
- C2 = C2 + len(indk)*np.dot(muk-mu,(muk-mu).T)
- C1 = C1 + 1e-8*np.trace(C1)*np.eye(D)#
- C2 = C2 + 1e-8*np.trace(C2)*np.eye(D)#
- C1 = 0.5*(C1+C1.T)#;% + 1E-8*trace(C1)*eye(D);
- C2 = 0.5*(C2+C2.T)#;% + 1E-8*trace(C2)*eye(D);
- dd,E = scipy.linalg.eigh(C1,C2) # ascending order
- #print dd.shape
- #print E.shape
- assert np.isnan(dd).any()==False
- assert np.iscomplex(dd).any()==False
- #[dd,ind] = sort(diag(dd),''descend'');
- #print dd
- dd = dd[::-1] #
- E = E[:,::-1]
- E = E/np.tile(np.sqrt((E**2).sum(axis=0,keepdims=True)),(D,1))
- #% They need not be orthogonal.
- #print dd.shape
- #print E.shape
- return (E,dd)
- def cwplot(fb_est,rx,t,fs:int,fn) -> None:
- #%% time
- fg,axs = subplots(1,2,figsize=(12,6))
- ax = axs[0]
- ax.plot(t, rx.T.real)
- ax.set_xlabel(''time [sec]'')
- ax.set_ylabel(''amplitude'')
- ax.set_title(''Noisy,jammed receive signal'')
- #%% periodogram
- if DTPG >= (t[-1]-t[0]):
- dt = (t[-1]-t[0])/4
- else:
- dt = DTPG
- dtw = 2*dt # seconds to window
- tstep = ceil(dt*fs)
- wind = ceil(dtw*fs);
- nfft = zeropadfactor*wind
- f,Sraw = signal.welch(rx.ravel(), fs,
- nperseg=wind,noverlap=tstep,nfft=nfft,
- return_onesided=False)
- if np.iscomplex(rx).any():
- f = np.fft.fftshift(f); Sraw = np.fft.fftshift(Sraw)
- ax=axs[1]
- ax.plot(f,Sraw,''r'',label=''raw signal'')
- fc_est = f[Sraw.argmax()]
- #ax.set_yscale(''log'')
- ax.set_xlim([fc_est-200,fc_est+200])
- ax.set_xlabel(''frequency [Hz]'')
- ax.set_ylabel(''amplitude'')
- ax.legend()
- esttxt=''''
- if fn is None: # simulation
- ax.axvline(ft+fb0,color=''red'',linestyle=''--'',label=''true freq.'')
- esttxt += f''true: {ft+fb0} Hz ''
- for e in fb_est:
- ax.axvline(e,color=''blue'',label=''est. freq.'')
- esttxt += '' est: '' + str(fb_est) +'' Hz''
- ax.set_title(esttxt)
- def cw_est(rx, fs:int, Ntone:int, method:str=''esprit'', usepython=False, useall=False):
- """
- estimate beat frequency using subspace frequency estimation techniques.
- This is much faster in Fortran,but to start using Python alone doesn''t require compiling Fortran.
- ESPRIT and RootMUSIC are two popular subspace techniques.
- Matlab''s rootmusic is a far inferior FFT-based method with very poor accuracy vs. my implementation.
- """
- assert isinstance(method,str)
- method = method.lower()
- tic = time()
- if method == ''esprit'':
- #%% ESPRIT
- if rx.ndim == 2:
- assert usepython,''Fortran not yet configured for multi-pulse case''
- Ntone *= 2
- if usepython or (Sc is None and Sr is None):
- print(''Python ESPRIT'')
- fb_est, sigma = esprit(rx, Ntone, Nblockest, fs)
- elif np.iscomplex(rx).any():
- print(''Fortran complex64 ESPRIT'')
- fb_est, sigma = Sc.subspace.esprit(rx,Ntone,Nblockest,fs)
- else: # real signal
- print(''Fortran float32 ESPRIT'')
- fb_est, sigma = Sr.subspace.esprit(rx,fs)
- fb_est = abs(fb_est)
- #%% ROOTMUSIC
- elif method == ''rootmusic'':
- fb_est, sigma = rootmusic(rx,fs)
- else:
- raise ValueError(f''unkNown estimation method: {method}'')
- print(f''computed via {method} in {time()-tic:.1f} seconds.'')
- #%% improvised process for CW only without notch filter
- # assumes first two results have largest singular values (from SVD)
- if not useall:
- i = sigma > 0.001 # arbitrary
- fb_est = fb_est[i]
- sigma = sigma[i]
- # if fb_est.size>1:
- # ii = np.argpartition(sigma,Ntone-1)[:Ntone-1]
- # fb_est = fb_est[ii]
- # sigma = sigma[ii]
- return fb_est, sigma

Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable
如何解决Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: ''numpy.ndarray'' object is not callable?
晚安, 尝试打印以下内容时,我在 jupyter 中遇到了 numpy 问题,并且得到了一个 错误: 需要注意的是python版本是3.8.8。 我先用 spyder 测试它,它运行正确,它给了我预期的结果
使用 Spyder:
import numpy as np
for i in range (5):
n = np.random.rand ()
print (n)
Results
0.6604903457995978
0.8236300859753154
0.16067650689842816
0.6967868357083673
0.4231597934445466
现在有了 jupyter
import numpy as np
for i in range (5):
n = np.random.rand ()
print (n)
-------------------------------------------------- ------
TypeError Traceback (most recent call last)
<ipython-input-78-0c6a801b3ea9> in <module>
2 for i in range (5):
3 n = np.random.rand ()
----> 4 print (n)
TypeError: ''numpy.ndarray'' object is not callable
感谢您对我如何在 Jupyter 中解决此问题的帮助。
非常感谢您抽出宝贵时间。
阿特,约翰”
解决方法
暂无找到可以解决该程序问题的有效方法,小编努力寻找整理中!
如果你已经找到好的解决方法,欢迎将解决方案带上本链接一起发送给小编。
小编邮箱:dio#foxmail.com (将#修改为@)

numpy.random.random & numpy.ndarray.astype & numpy.arange
今天看到这样一句代码:
xb = np.random.random((nb, d)).astype(''float32'') #创建一个二维随机数矩阵(nb行d列)
xb[:, 0] += np.arange(nb) / 1000. #将矩阵第一列的每个数加上一个值要理解这两句代码需要理解三个函数
1、生成随机数
numpy.random.random(size=None)
size为None时,返回float。
size不为None时,返回numpy.ndarray。例如numpy.random.random((1,2)),返回1行2列的numpy数组
2、对numpy数组中每一个元素进行类型转换
numpy.ndarray.astype(dtype)
返回numpy.ndarray。例如 numpy.array([1, 2, 2.5]).astype(int),返回numpy数组 [1, 2, 2]
3、获取等差数列
numpy.arange([start,]stop,[step,]dtype=None)
功能类似python中自带的range()和numpy中的numpy.linspace
返回numpy数组。例如numpy.arange(3),返回numpy数组[0, 1, 2]

numpy.ravel()/numpy.flatten()/numpy.squeeze()
numpy.ravel(a, order=''C'')
Return a flattened array
numpy.chararray.flatten(order=''C'')
Return a copy of the array collapsed into one dimension
numpy.squeeze(a, axis=None)
Remove single-dimensional entries from the shape of an array.
相同点: 将多维数组 降为 一维数组
不同点:
ravel() 返回的是视图(view),意味着改变元素的值会影响原始数组元素的值;
flatten() 返回的是拷贝,意味着改变元素的值不会影响原始数组;
squeeze()返回的是视图(view),仅仅是将shape中dimension为1的维度去掉;
ravel()示例:
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.ravel()
16 print("a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19
20 print(a)
21 log_type(''a'',a)
flatten()示例
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.flatten()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)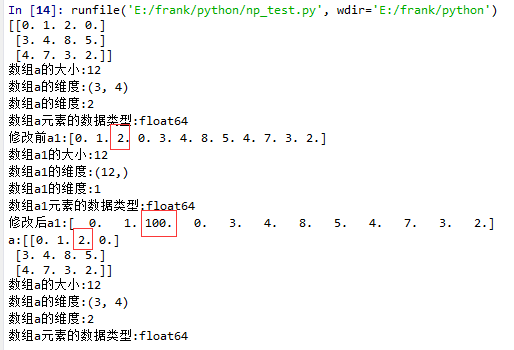
squeeze()示例:
1. 没有single-dimensional entries的情况
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.squeeze()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)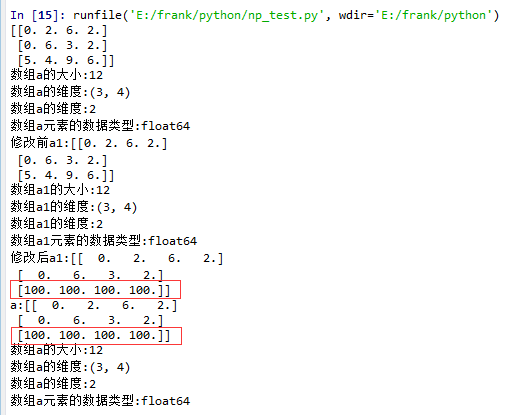
从结果中可以看到,当没有single-dimensional entries时,squeeze()返回额数组对象是一个view,而不是copy。
2. 有single-dimentional entries 的情况
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((1,3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.squeeze()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)

Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性
一、Numpy数组创建
part 1:np.linspace(起始值,终止值,元素总个数
import numpy as np
''''''
numpy中的ndarray数组
''''''
ary = np.array([1, 2, 3, 4, 5])
print(ary)
ary = ary * 10
print(ary)
''''''
ndarray对象的创建
''''''
# 创建二维数组
# np.array([[],[],...])
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(a)
# np.arange(起始值, 结束值, 步长(默认1))
b = np.arange(1, 10, 1)
print(b)
print("-------------np.zeros(数组元素个数, dtype=''数组元素类型'')-----")
# 创建一维数组:
c = np.zeros(10)
print(c, ''; c.dtype:'', c.dtype)
# 创建二维数组:
print(np.zeros ((3,4)))
print("----------np.ones(数组元素个数, dtype=''数组元素类型'')--------")
# 创建一维数组:
d = np.ones(10, dtype=''int64'')
print(d, ''; d.dtype:'', d.dtype)
# 创建三维数组:
print(np.ones( (2,3,4), dtype=np.int32 ))
# 打印维度
print(np.ones( (2,3,4), dtype=np.int32 ).ndim) # 返回:3(维)
结果图:

part 2 :np.linspace ( 起始值,终止值,元素总个数)
import numpy as np
a = np.arange( 10, 30, 5 )
b = np.arange( 0, 2, 0.3 )
c = np.arange(12).reshape(4,3)
d = np.random.random((2,3)) # 取-1到1之间的随机数,要求设置为诶2行3列的结构
print(a)
print(b)
print(c)
print(d)
print("-----------------")
from numpy import pi
print(np.linspace( 0, 2*pi, 100 ))
print("-------------np.linspace(起始值,终止值,元素总个数)------------------")
print(np.sin(np.linspace( 0, 2*pi, 100 )))
结果图:

二、Numpy的ndarray对象属性:
数组的结构:array.shape
数组的维度:array.ndim
元素的类型:array.dtype
数组元素的个数:array.size
数组的索引(下标):array[0]
''''''
数组的基本属性
''''''
import numpy as np
print("--------------------案例1:------------------------------")
a = np.arange(15).reshape(3, 5)
print(a)
print(a.shape) # 打印数组结构
print(len(a)) # 打印有多少行
print(a.ndim) # 打印维度
print(a.dtype) # 打印a数组内的元素的数据类型
# print(a.dtype.name)
print(a.size) # 打印数组的总元素个数
print("-------------------案例2:---------------------------")
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a)
# 测试数组的基本属性
print(''a.shape:'', a.shape)
print(''a.size:'', a.size)
print(''len(a):'', len(a))
# a.shape = (6, ) # 此格式可将原数组结构变成1行6列的数据结构
# print(a, ''a.shape:'', a.shape)
# 数组元素的索引
ary = np.arange(1, 28)
ary.shape = (3, 3, 3) # 创建三维数组
print("ary.shape:",ary.shape,"\n",ary )
print("-----------------")
print(''ary[0]:'', ary[0])
print(''ary[0][0]:'', ary[0][0])
print(''ary[0][0][0]:'', ary[0][0][0])
print(''ary[0,0,0]:'', ary[0, 0, 0])
print("-----------------")
# 遍历三维数组:遍历出数组里的每个元素
for i in range(ary.shape[0]):
for j in range(ary.shape[1]):
for k in range(ary.shape[2]):
print(ary[i, j, k], end='' '')
结果图:

关于Python numpy 模块-iscomplex() 实例源码和python中numpy模块的问题就给大家分享到这里,感谢你花时间阅读本站内容,更多关于Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable、numpy.random.random & numpy.ndarray.astype & numpy.arange、numpy.ravel()/numpy.flatten()/numpy.squeeze()、Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性等相关知识的信息别忘了在本站进行查找喔。
本文标签:





