这篇文章主要围绕Pythonnumpy模块-isrealobj()实例源码和python中numpy模块展开,旨在为您提供一份详细的参考资料。我们将全面介绍Pythonnumpy模块-isrealob
这篇文章主要围绕Python numpy 模块-isrealobj() 实例源码和python中numpy模块展开,旨在为您提供一份详细的参考资料。我们将全面介绍Python numpy 模块-isrealobj() 实例源码的优缺点,解答python中numpy模块的相关问题,同时也会为您带来Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable、numpy.random.random & numpy.ndarray.astype & numpy.arange、numpy.ravel()/numpy.flatten()/numpy.squeeze()、Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性的实用方法。
本文目录一览:- Python numpy 模块-isrealobj() 实例源码(python中numpy模块)
- Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable
- numpy.random.random & numpy.ndarray.astype & numpy.arange
- numpy.ravel()/numpy.flatten()/numpy.squeeze()
- Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性

Python numpy 模块-isrealobj() 实例源码(python中numpy模块)
Python numpy 模块,isrealobj() 实例源码
我们从Python开源项目中,提取了以下14个代码示例,用于说明如何使用numpy.isrealobj()。
- def operate(self, x):
- """
- Apply the separable filter to the signal vector *x*.
- """
- X = NP.fft.fftn(x, s=self.k_full)
- if NP.isrealobj(self.h) and NP.isrealobj(x):
- y = NP.real(NP.fft.ifftn(self.H * X))
- else:
- y = NP.fft.ifftn(self.H * X)
- if self.mode == ''full'' or self.mode == ''circ'':
- return y
- elif self.mode == ''valid'':
- slice_list = []
- for i in range(self.ndim):
- if self.m[i]-1 == 0:
- slice_list.append(slice(None, None, None))
- else:
- slice_list.append(slice(self.m[i]-1, -(self.m[i]-1), None))
- return y[slice_list]
- else:
- assert(False)
- def correlate_periodic(a, v=None):
- """Cross-correlation of two 1-dimensional periodic sequences.
- a and v must be sequences with the same length. If v is not specified,it is
- assumed to be the same as a (i.e. the function computes auto-correlation).
- :param a: input sequence #1
- :param v: input sequence #2
- :returns: discrete periodic cross-correlation of a and v
- """
- a_fft = _np.fft.fft(_np.asarray(a))
- if v is None:
- v_cfft = a_fft.conj()
- else:
- v_cfft = _np.fft.fft(_np.asarray(v)).conj()
- x = _np.fft.ifft(a_fft * v_cfft)
- if _np.isrealobj(a) and (v is None or _np.isrealobj(v)):
- x = x.real
- return x
- def inverse(self, encoded, duration=None):
- ''''''Inverse static tag transformation''''''
- ann = jams.Annotation(namespace=self.namespace, duration=duration)
- if np.isrealobj(encoded):
- detected = (encoded >= 0.5)
- else:
- detected = encoded
- for vd in self.encoder.inverse_transform(np.atleast_2d(detected))[0]:
- vid = np.flatnonzero(self.encoder.transform(np.atleast_2d(vd)))
- ann.append(time=0,
- duration=duration,
- value=vd,
- confidence=encoded[vid])
- return ann
- def decode_events(self, encoded):
- ''''''Decode labeled events into (time,value) pairs
- Parameters
- ----------
- encoded : np.ndarray,shape=(n_frames,m)
- Frame-level annotation encodings as produced by ``encode_events``.
- Real-valued inputs are thresholded at 0.5.
- Returns
- -------
- [(time,value)] : iterable of tuples
- where `time` is the event time and `value` is an
- np.ndarray,shape=(m,) of the encoded value at that time
- ''''''
- if np.isrealobj(encoded):
- encoded = (encoded >= 0.5)
- times = frames_to_time(np.arange(encoded.shape[0]),
- sr=self.sr,
- hop_length=self.hop_length)
- return zip(times, encoded)
- def atal(x, order, num_coefs):
- x = np.atleast_1d(x)
- n = x.size
- if x.ndim > 1:
- raise ValueError("Only rank 1 input supported for Now.")
- if not np.isrealobj(x):
- raise ValueError("Only real input supported for Now.")
- a, e, kk = lpc(x, order)
- c = np.zeros(num_coefs)
- c[0] = a[0]
- for m in range(1, order+1):
- c[m] = - a[m]
- for k in range(1, m):
- c[m] += (float(k)/float(m)-1)*a[k]*c[m-k]
- for m in range(order+1, num_coefs):
- for k in range(1, order+1):
- c[m] += (float(k)/float(m)-1)*a[k]*c[m-k]
- return c
- def test_poly(self):
- assert_array_almost_equal(np.poly([3, -np.sqrt(2), np.sqrt(2)]),
- [1, -3, -2, 6])
- # From matlab docs
- A = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
- assert_array_almost_equal(np.poly(A), [1, -6, -72, -27])
- # Should produce real output for perfect conjugates
- assert_(np.isrealobj(np.poly([+1.082j, +2.613j, -2.613j, -1.082j])))
- assert_(np.isrealobj(np.poly([0+1j, -0+-1j, 1+2j,
- 1-2j, 1.+3.5j, 1-3.5j])))
- assert_(np.isrealobj(np.poly([1j, -1j, 1-2j, 1+3j, 1-3.j])))
- assert_(np.isrealobj(np.poly([1j, 1-2j])))
- assert_(np.isrealobj(np.poly([1j, 2j, -2j])))
- assert_(np.isrealobj(np.poly([1j, -1j])))
- assert_(np.isrealobj(np.poly([1, -1])))
- assert_(np.iscomplexobj(np.poly([1j, -1.0000001j])))
- np.random.seed(42)
- a = np.random.randn(100) + 1j*np.random.randn(100)
- assert_(np.isrealobj(np.poly(np.concatenate((a, np.conjugate(a))))))
- def polyval(self, chebcoeff):
- """
- Compute the interpolation values at Chebyshev points.
- chebcoeff: Chebyshev coefficients
- """
- N = len(chebcoeff)
- if N == 1:
- return chebcoeff
- data = even_data(chebcoeff)/2
- data[0] *= 2
- data[N-1] *= 2
- fftdata = 2*(N-1)*fftpack.ifft(data, axis=0)
- complex_values = fftdata[:N]
- # convert to real if input was real
- if np.isrealobj(chebcoeff):
- values = np.real(complex_values)
- else:
- values = complex_values
- return values
- def dct(data):
- """
- Compute DCT using FFT
- """
- N = len(data)//2
- fftdata = fftpack.fft(data, axis=0)[:N+1]
- fftdata /= N
- fftdata[0] /= 2.
- fftdata[-1] /= 2.
- if np.isrealobj(data):
- data = np.real(fftdata)
- else:
- data = fftdata
- return data
- # ----------------------------------------------------------------
- # Add overloaded operators
- # ----------------------------------------------------------------
- def isreal(self):
- """Returns True if entire signal is real."""
- return np.all(np.isreal(self._ydata))
- # return np.isrealobj(self._ydata)
- def fftconv(a, b, axes=(0,1)):
- """
- Compute a multi-dimensional convolution via the discrete Fourier Transform.
- Parameters
- ----------
- a : array_like
- Input array
- b : array_like
- Input array
- axes : sequence of ints,optional (default (0,1))
- Axes on which to perform convolution
- Returns
- -------
- ab : ndarray
- Convolution of input arrays,a and b,along specified axes
- """
- if np.isrealobj(a) and np.isrealobj(b):
- fft = rfftn
- ifft = irfftn
- else:
- fft = fftn
- ifft = ifftn
- dims = np.maximum([a.shape[i] for i in axes], [b.shape[i] for i in axes])
- af = fft(a, dims, axes)
- bf = fft(b, axes)
- return ifft(af*bf, axes)
- def evaluate(self, ind, **kwargs):
- """
- Note that math functions used in the solutions are imported from either
- utilities.fitness.math_functions or called from numpy.
- :param ind: An individual to be evaluated.
- :param kwargs: An optional parameter for problems with training/test
- data. Specifies the distribution (i.e. training or test) upon which
- evaluation is to be performed.
- :return: The fitness of the evaluated individual.
- """
- dist = kwargs.get(''dist'', ''training'')
- if dist == "training":
- # Set training datasets.
- x = self.training_in
- y = self.training_exp
- elif dist == "test":
- # Set test datasets.
- x = self.test_in
- y = self.test_exp
- else:
- raise ValueError("UnkNown dist: " + dist)
- if params[''OPTIMIZE_CONSTANTS'']:
- # if we are training,then optimize the constants by
- # gradient descent and save the resulting phenotype
- # string as ind.phenotype_with_c0123 (eg x[0] +
- # c[0] * x[1]**c[1]) and values for constants as
- # ind.opt_consts (eg (0.5,0.7). Later,when testing,
- # use the saved string and constants to evaluate.
- if dist == "training":
- return optimize_constants(x, y, ind)
- else:
- # this string has been created during training
- phen = ind.phenotype_consec_consts
- c = ind.opt_consts
- # phen will refer to x (ie test_in),and possibly to c
- yhat = eval(phen)
- assert np.isrealobj(yhat)
- # let''s always call the error function with the
- # true values first,the estimate second
- return params[''ERROR_METRIC''](y, yhat)
- else:
- # phenotype won''t refer to C
- yhat = eval(ind.phenotype)
- assert np.isrealobj(yhat)
- # let''s always call the error function with the true
- # values first,the estimate second
- return params[''ERROR_METRIC''](y, yhat)
- def periodogram(x, nfft=None, fs=1):
- """Compute the periodogram of the given signal,with the given fft size.
- Parameters
- ----------
- x : array-like
- input signal
- nfft : int
- size of the fft to compute the periodogram. If None (default),the
- length of the signal is used. if nfft > n,the signal is 0 padded.
- fs : float
- Sampling rate. By default,is 1 (normalized frequency. e.g. 0.5 is the
- Nyquist limit).
- Returns
- -------
- pxx : array-like
- The psd estimate.
- fgrid : array-like
- Frequency grid over which the periodogram was estimated.
- Examples
- --------
- Generate a signal with two sinusoids,and compute its periodogram:
- >>> fs = 1000
- >>> x = np.sin(2 * np.pi * 0.1 * fs * np.linspace(0,0.5,0.5*fs))
- >>> x += np.sin(2 * np.pi * 0.2 * fs * np.linspace(0,0.5*fs))
- >>> px,fx = periodogram(x,512,fs)
- Notes
- -----
- Only real signals supported for Now.
- Returns the one-sided version of the periodogram.
- discrepency with matlab: matlab compute the psd in unit of power / radian /
- sample,and we compute the psd in unit of power / sample: to get the same
- result as matlab,just multiply the result from talkBox by 2pi"""
- x = np.atleast_1d(x)
- n = x.size
- if x.ndim > 1:
- raise ValueError("Only rank 1 input supported for Now.")
- if not np.isrealobj(x):
- raise ValueError("Only real input supported for Now.")
- if not nfft:
- nfft = n
- if nfft < n:
- raise ValueError("nfft < signal size not supported yet")
- pxx = np.abs(fft(x, nfft)) ** 2
- if nfft % 2 == 0:
- pn = nfft / 2 + 1
- else:
- pn = (nfft + 1 )/ 2
- fgrid = np.linspace(0, fs * 0.5, pn)
- return pxx[:pn] / (n * fs), fgrid
- def arspec(x, fs=1):
- """Compute the spectral density using an AR model.
- An AR model of the signal is estimated through the Yule-Walker equations;
- the estimated AR coefficient are then used to compute the spectrum,which
- can be computed explicitely for AR models.
- Parameters
- ----------
- x : array-like
- input signal
- order : int
- Order of the LPC computation.
- nfft : int
- size of the fft to compute the periodogram. If None (default),is 1 (normalized frequency. e.g. 0.5 is the
- Nyquist limit).
- Returns
- -------
- pxx : array-like
- The psd estimate.
- fgrid : array-like
- Frequency grid over which the periodogram was estimated.
- """
- x = np.atleast_1d(x)
- n = x.size
- if x.ndim > 1:
- raise ValueError("Only rank 1 input supported for Now.")
- if not np.isrealobj(x):
- raise ValueError("Only real input supported for Now.")
- if not nfft:
- nfft = n
- a, k = lpc(x, order)
- # This is not enough to deal correctly with even/odd size
- if nfft % 2 == 0:
- pn = nfft / 2 + 1
- else:
- pn = (nfft + 1 )/ 2
- px = 1 / np.fft.fft(a, nfft)[:pn]
- pxx = np.real(np.conj(px) * px)
- pxx /= fs / e
- fx = np.linspace(0, pxx.size)
- return pxx, fx
- def _write_raw_buffer(fid, buf, cals, fmt, inv_comp):
- """Write raw buffer
- Parameters
- ----------
- fid : file descriptor
- an open raw data file.
- buf : array
- The buffer to write.
- cals : array
- Calibration factors.
- fmt : str
- ''short'',''int'',''single'',or ''double'' for 16/32 bit int or 32/64 bit
- float for each item. This will be doubled for complex datatypes. Note
- that short and int formats cannot be used for complex data.
- inv_comp : array | None
- The CTF compensation matrix used to revert compensation
- change when reading.
- """
- if buf.shape[0] != len(cals):
- raise ValueError(''buffer and calibration sizes do not match'')
- if fmt not in [''short'', ''int'', ''single'', ''double'']:
- raise ValueError(''fmt must be "short","single",or "double"'')
- if np.isrealobj(buf):
- if fmt == ''short'':
- write_function = write_dau_pack16
- elif fmt == ''int'':
- write_function = write_int
- elif fmt == ''single'':
- write_function = write_float
- else:
- write_function = write_double
- else:
- if fmt == ''single'':
- write_function = write_complex64
- elif fmt == ''double'':
- write_function = write_complex128
- else:
- raise ValueError(''only "single" and "double" supported for ''
- ''writing complex data'')
- if inv_comp is not None:
- buf = np.dot(inv_comp / np.ravel(cals)[:, None], buf)
- else:
- buf = buf / np.ravel(cals)[:, None]
- write_function(fid, FIFF.FIFF_DATA_BUFFER, buf)

Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable
如何解决Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: ''numpy.ndarray'' object is not callable?
晚安, 尝试打印以下内容时,我在 jupyter 中遇到了 numpy 问题,并且得到了一个 错误: 需要注意的是python版本是3.8.8。 我先用 spyder 测试它,它运行正确,它给了我预期的结果
使用 Spyder:
import numpy as np
for i in range (5):
n = np.random.rand ()
print (n)
Results
0.6604903457995978
0.8236300859753154
0.16067650689842816
0.6967868357083673
0.4231597934445466
现在有了 jupyter
import numpy as np
for i in range (5):
n = np.random.rand ()
print (n)
-------------------------------------------------- ------
TypeError Traceback (most recent call last)
<ipython-input-78-0c6a801b3ea9> in <module>
2 for i in range (5):
3 n = np.random.rand ()
----> 4 print (n)
TypeError: ''numpy.ndarray'' object is not callable
感谢您对我如何在 Jupyter 中解决此问题的帮助。
非常感谢您抽出宝贵时间。
阿特,约翰”
解决方法
暂无找到可以解决该程序问题的有效方法,小编努力寻找整理中!
如果你已经找到好的解决方法,欢迎将解决方案带上本链接一起发送给小编。
小编邮箱:dio#foxmail.com (将#修改为@)

numpy.random.random & numpy.ndarray.astype & numpy.arange
今天看到这样一句代码:
xb = np.random.random((nb, d)).astype(''float32'') #创建一个二维随机数矩阵(nb行d列)
xb[:, 0] += np.arange(nb) / 1000. #将矩阵第一列的每个数加上一个值要理解这两句代码需要理解三个函数
1、生成随机数
numpy.random.random(size=None)
size为None时,返回float。
size不为None时,返回numpy.ndarray。例如numpy.random.random((1,2)),返回1行2列的numpy数组
2、对numpy数组中每一个元素进行类型转换
numpy.ndarray.astype(dtype)
返回numpy.ndarray。例如 numpy.array([1, 2, 2.5]).astype(int),返回numpy数组 [1, 2, 2]
3、获取等差数列
numpy.arange([start,]stop,[step,]dtype=None)
功能类似python中自带的range()和numpy中的numpy.linspace
返回numpy数组。例如numpy.arange(3),返回numpy数组[0, 1, 2]

numpy.ravel()/numpy.flatten()/numpy.squeeze()
numpy.ravel(a, order=''C'')
Return a flattened array
numpy.chararray.flatten(order=''C'')
Return a copy of the array collapsed into one dimension
numpy.squeeze(a, axis=None)
Remove single-dimensional entries from the shape of an array.
相同点: 将多维数组 降为 一维数组
不同点:
ravel() 返回的是视图(view),意味着改变元素的值会影响原始数组元素的值;
flatten() 返回的是拷贝,意味着改变元素的值不会影响原始数组;
squeeze()返回的是视图(view),仅仅是将shape中dimension为1的维度去掉;
ravel()示例:
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.ravel()
16 print("a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19
20 print(a)
21 log_type(''a'',a)
flatten()示例
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.flatten()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)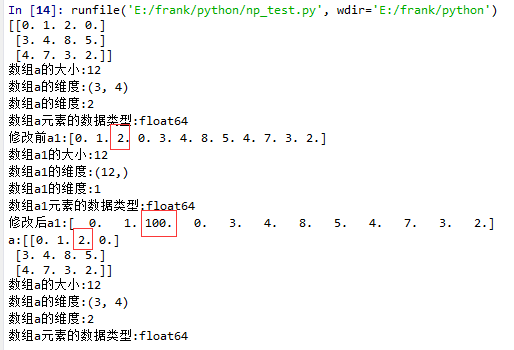
squeeze()示例:
1. 没有single-dimensional entries的情况
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.squeeze()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)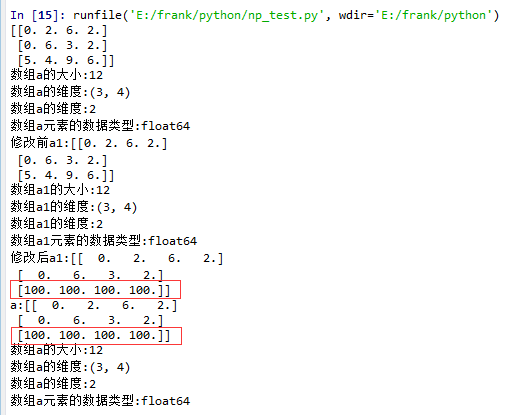
从结果中可以看到,当没有single-dimensional entries时,squeeze()返回额数组对象是一个view,而不是copy。
2. 有single-dimentional entries 的情况
1 import matplotlib.pyplot as plt
2 import numpy as np
3
4 def log_type(name,arr):
5 print("数组{}的大小:{}".format(name,arr.size))
6 print("数组{}的维度:{}".format(name,arr.shape))
7 print("数组{}的维度:{}".format(name,arr.ndim))
8 print("数组{}元素的数据类型:{}".format(name,arr.dtype))
9 #print("数组:{}".format(arr.data))
10
11 a = np.floor(10*np.random.random((1,3,4)))
12 print(a)
13 log_type(''a'',a)
14
15 a1 = a.squeeze()
16 print("修改前a1:{}".format(a1))
17 log_type(''a1'',a1)
18 a1[2] = 100
19 print("修改后a1:{}".format(a1))
20
21 print("a:{}".format(a))
22 log_type(''a'',a)

Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性
一、Numpy数组创建
part 1:np.linspace(起始值,终止值,元素总个数
import numpy as np
''''''
numpy中的ndarray数组
''''''
ary = np.array([1, 2, 3, 4, 5])
print(ary)
ary = ary * 10
print(ary)
''''''
ndarray对象的创建
''''''
# 创建二维数组
# np.array([[],[],...])
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(a)
# np.arange(起始值, 结束值, 步长(默认1))
b = np.arange(1, 10, 1)
print(b)
print("-------------np.zeros(数组元素个数, dtype=''数组元素类型'')-----")
# 创建一维数组:
c = np.zeros(10)
print(c, ''; c.dtype:'', c.dtype)
# 创建二维数组:
print(np.zeros ((3,4)))
print("----------np.ones(数组元素个数, dtype=''数组元素类型'')--------")
# 创建一维数组:
d = np.ones(10, dtype=''int64'')
print(d, ''; d.dtype:'', d.dtype)
# 创建三维数组:
print(np.ones( (2,3,4), dtype=np.int32 ))
# 打印维度
print(np.ones( (2,3,4), dtype=np.int32 ).ndim) # 返回:3(维)
结果图:

part 2 :np.linspace ( 起始值,终止值,元素总个数)
import numpy as np
a = np.arange( 10, 30, 5 )
b = np.arange( 0, 2, 0.3 )
c = np.arange(12).reshape(4,3)
d = np.random.random((2,3)) # 取-1到1之间的随机数,要求设置为诶2行3列的结构
print(a)
print(b)
print(c)
print(d)
print("-----------------")
from numpy import pi
print(np.linspace( 0, 2*pi, 100 ))
print("-------------np.linspace(起始值,终止值,元素总个数)------------------")
print(np.sin(np.linspace( 0, 2*pi, 100 )))
结果图:

二、Numpy的ndarray对象属性:
数组的结构:array.shape
数组的维度:array.ndim
元素的类型:array.dtype
数组元素的个数:array.size
数组的索引(下标):array[0]
''''''
数组的基本属性
''''''
import numpy as np
print("--------------------案例1:------------------------------")
a = np.arange(15).reshape(3, 5)
print(a)
print(a.shape) # 打印数组结构
print(len(a)) # 打印有多少行
print(a.ndim) # 打印维度
print(a.dtype) # 打印a数组内的元素的数据类型
# print(a.dtype.name)
print(a.size) # 打印数组的总元素个数
print("-------------------案例2:---------------------------")
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a)
# 测试数组的基本属性
print(''a.shape:'', a.shape)
print(''a.size:'', a.size)
print(''len(a):'', len(a))
# a.shape = (6, ) # 此格式可将原数组结构变成1行6列的数据结构
# print(a, ''a.shape:'', a.shape)
# 数组元素的索引
ary = np.arange(1, 28)
ary.shape = (3, 3, 3) # 创建三维数组
print("ary.shape:",ary.shape,"\n",ary )
print("-----------------")
print(''ary[0]:'', ary[0])
print(''ary[0][0]:'', ary[0][0])
print(''ary[0][0][0]:'', ary[0][0][0])
print(''ary[0,0,0]:'', ary[0, 0, 0])
print("-----------------")
# 遍历三维数组:遍历出数组里的每个元素
for i in range(ary.shape[0]):
for j in range(ary.shape[1]):
for k in range(ary.shape[2]):
print(ary[i, j, k], end='' '')
结果图:

今天关于Python numpy 模块-isrealobj() 实例源码和python中numpy模块的介绍到此结束,谢谢您的阅读,有关Jupyter 中的 Numpy 在打印时出错(Python 版本 3.8.8):TypeError: 'numpy.ndarray' object is not callable、numpy.random.random & numpy.ndarray.astype & numpy.arange、numpy.ravel()/numpy.flatten()/numpy.squeeze()、Numpy:数组创建 numpy.arrray() , numpy.arange()、np.linspace ()、数组基本属性等更多相关知识的信息可以在本站进行查询。
本文标签:





