对于想了解numpy.sum和numpy.cumsum之间的不同表现是什么?的读者,本文将是一篇不可错过的文章,我们将详细介绍numpy.sum()的使用,并且为您提供关于2021-05-27:定义何
对于想了解numpy.sum 和 numpy.cumsum 之间的不同表现是什么?的读者,本文将是一篇不可错过的文章,我们将详细介绍numpy.sum()的使用,并且为您提供关于2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。、clear,cumsum,sum,numel,double,zeros,ones,abs,histeq,max/min、Cumsum 基于列的条件,更改条件再次开始 cumsum、cumsum累计函数系列:pd.cumsum()、pd.cumprod()、pd.cummax()、pd.cummin()的有价值信息。
本文目录一览:- numpy.sum 和 numpy.cumsum 之间的不同表现是什么?(numpy.sum()的使用)
- 2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。
- clear,cumsum,sum,numel,double,zeros,ones,abs,histeq,max/min
- Cumsum 基于列的条件,更改条件再次开始 cumsum
- cumsum累计函数系列:pd.cumsum()、pd.cumprod()、pd.cummax()、pd.cummin()

numpy.sum 和 numpy.cumsum 之间的不同表现是什么?(numpy.sum()的使用)
如何解决numpy.sum 和 numpy.cumsum 之间的不同表现是什么?
如果我的理解是正确的,np.sum 和 np.cumsum 都需要 O(n) 时间。但是,当我对同一个矩阵按顺序(在不同的轴上)执行这两个操作时,似乎 np.sum 和 np.cumsum 的顺序使整体性能完全不同,尽管结果与预期相同。
如果我先对每一行沿列方向 (np.cumsum) 执行 axis=1,然后对所有行 (np.sum) 执行 axis=0,它将需要时间更长。
如果我先沿行 (np.sum) 执行 axis=0,然后对一维数组执行 np.cumsum,则需要更短的时间。
我的假设是 np.cumsum 将在数据分配/操作上花费更多时间,因为它会产生比 np.sum 更多的数据,因此如果 {{} 的操作更多,它将花费更长的时间1}}。
这是我的测试代码和结果
np.cumsum
结果是
import numpy as npimport timeb = np.zeros((1000,1000))for i in range(1000):b[i] = np.array(range(1000))time_start = time.time()for i in range(1000):c = np.cumsum(b,axis=1)d = np.sum(c,axis=0)time_end = time.time()print(f"np.sum(np.cumsum(...)) time: {time_end - time_start}")time_start = time.time()for i in range(1000):c = np.cumsum(np.sum(b,axis=0))time_end = time.time()print(f"np.cumsum(np.sum(...)) time: {time_end - time_start}")
解决方法
看看应用于小阵列的替代方案。
In [45]: b = np.arange(24).reshape(4,6)In [46]: bOut[46]:array([[ 0,1,2,3,4,5],[ 6,7,8,9,10,11],[12,13,14,15,16,17],[18,19,20,21,22,23]])
sum(cumsum(b)):
In [47]: np.cumsum(b,axis=1) # same shape as bOut[47]:array([[ 0,6,15],[ 6,30,40,51],[ 12,25,39,54,70,87],[ 18,37,57,78,100,123]])In [48]: np.sum(_,axis=0)Out[48]: array([ 36,76,120,168,220,276])
求和:
In [49]: np.sum(b,axis=0) # much reduced arrayOut[49]: array([36,44,48,52,56])In [50]: np.cumsum(_)Out[50]: array([ 36,276])
虽然第一步对相同数量的元素进行操作,整个 b,但当 sum 首先完成时,第二步使用一个大大减少的数组。
实际上对于这个小样本,时间差异很小:
In [57]: timeit np.sum(np.cumsum(b,axis=1),axis=0)17.8 µs ± 29.5 ns per loop (mean ± std. dev. of 7 runs,100000 loops each)In [58]: timeit np.cumsum(np.sum(b,axis=0))16.1 µs ± 30.5 ns per loop (mean ± std. dev. of 7 runs,100000 loops each)
但对于更大的阵列,由于减少而节省的时间变得显着:
In [59]: b = np.random.randint(0,1000,(1000,1000))In [60]: timeit np.sum(np.cumsum(b,axis=0)5.11 ms ± 9.99 µs per loop (mean ± std. dev. of 7 runs,100 loops each)In [61]: timeit np.cumsum(np.sum(b,axis=0))1.64 ms ± 649 ns per loop (mean ± std. dev. of 7 runs,1000 loops each)
单独看第一步:
In [62]: timeit np.cumsum(b,axis=1)3.73 ms ± 12.6 µs per loop (mean ± std. dev. of 7 runs,100 loops each)In [63]: timeit np.sum(b,axis=0)1.62 ms ± 1.7 µs per loop (mean ± std. dev. of 7 runs,1000 loops each)
cumsum,因为它返回一个完整的 b.shape 数组比较慢。
O(n) 告诉我们有关操作如何扩展的一些信息,例如在对小数组与大数组进行操作时。但它不能用于将一个操作与另一个进行比较。此外,使用 numpy,核心计算在编译代码中快速完成,但内存管理和其他设置问题可能会占用核心时间。
编辑
np.sum 本质上是 np.add.reduce:
In [79]: timeit np.add.reduce(b,axis=0)1.59 ms ± 4.73 µs per loop (mean ± std. dev. of 7 runs,1000 loops each)In [80]: timeit np.sum(b,axis=0)1.64 ms ± 5.48 µs per loop (mean ± std. dev. of 7 runs,1000 loops each)
而 np.cumsum 是 np.add.accumulate:
,
In [81]: timeit np.cumsum(b,axis=0)10.2 ms ± 357 µs per loop (mean ± std. dev. of 7 runs,100 loops each)In [82]: timeit np.add.accumulate(b,axis=0)10 ms ± 14.6 µs per loop (mean ± std. dev. of 7 runs,100 loops each)
如果我的理解是正确的,np.sum 和 np.cumsum 都需要 O(n) 时间。
正确(假设输入相同)!
np.sum 和 np.cumsum 的顺序似乎让整体性能大不相同
np.cumsum 在相同输入上比 np.sum 更昂贵,因为 np.cumsum 需要分配和写入输出数组(这可能非常大)。此外,假设浮点运算是关联的,np.sum 的实现可以很容易地优化,而优化 np.cumsum 却非常困难。
我的假设是 np.cumsum 会在数据分配/操作上花费更多时间,因为它会比 np.sum 产生更多数据,所以如果 np.cumsum 的操作更多,它会花费更长的时间。
>问题是第一个实现比第二个有更多的工作要做。这主要是它变慢的原因,特别是因为内存读/写。实际上,np.cumsum 在第一个实现中产生了一个大的 2D 数组,必须由 np.sum 计算。 写入和读取这个临时数组的开销很大。在该示例中,第一个实现需要将 14.9 GiB 移出/移出内存层次结构(可能在 RAM 中),仅用于临时数组。请注意,构建临时数组也会使计算不那么缓存友好,因为它需要更多空间,因此 b 和 c 可能不再适合缓存({ {1}} 和 b 在我的机器上各占用 8 MiB,而我的 CPU 有一个 9 MiB 的 L3 缓存,这意味着不是两者都可以放入缓存中)而不是第二个实现。 RAM 的吞吐量通常比 CPU 缓存之一小得多。
请注意,第二个实现也会生成临时数组。这个版本应该分配与第一个一样多的临时数组。然而,第二个实现产生了1000倍小的临时数组!因此,在此版本中对 c 的调用要快得多。在我的机器上,np.cumsum 主要存储在快速 L3 缓存中,临时数组存储在非常快的 L1 缓存中。

2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。
2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。给定一个整数 num,判断它是不是某个数的 step sum?
福大大 答案 2021-05-27:
方法一:
自然智慧即可。二分法。在 0 到 num 之间找中点,然后求中点的 step sum。如果 step sum 太大,取左边;如果 step sum 太小,取右边。时间复杂度是 (log2N)*(log10N)。
方法二:
1. 求出不大于 num 的最大的全 1 数,然后 num / 全 1 数。如果商大于等于 10,直接返回 false。
2. 看余数。
2.1. 当余数不为 0 时,num = 余数,全 1 数 =(全 1 数 / 10),重复步骤 1。
2.2. 当余数为 0 时,返回 true。
时间复杂度是 log10N。
代码用 golang 编写。代码如下:
package main
import "fmt"
//05
func main() {
count := 0
for i := 1; i <= 11111; i++ {
ret1 := isStepSum1(i)
ret2 := isStepSum2(i)
fmt.Println(i, ret1, ret2)
count++
}
fmt.Println("正确数 = ", count)
}
//方法1
func isStepSum1(stepSum int) bool {
L := 0
R := stepSum
M := 0
cur := 0
for L <= R {
M = L + (R-L)>>1
cur = getStepSum(M)
if cur == stepSum {
return true
} else if cur < stepSum {
L = M + 1
} else {
R = M - 1
}
}
return false
}
func getStepSum(num int) int {
sum := 0
for num != 0 {
sum += num
num /= 10
}
return sum
}
//方法2
func isStepSum2(stepSum int) bool {
global111 := getGlobal111(stepSum)
for global111 > 0 {
quotient := stepSum / global111 //商
remainder := stepSum % global111 //余数
if quotient >= 10 {
return false
}
global111 /= 10
stepSum = remainder
}
return true
}
func getGlobal111(num int) int {
ans := 1
anstemp := 11
for anstemp <= num {
ans = anstemp
anstemp *= 10
anstemp++
}
return ans
}执行结果如下:
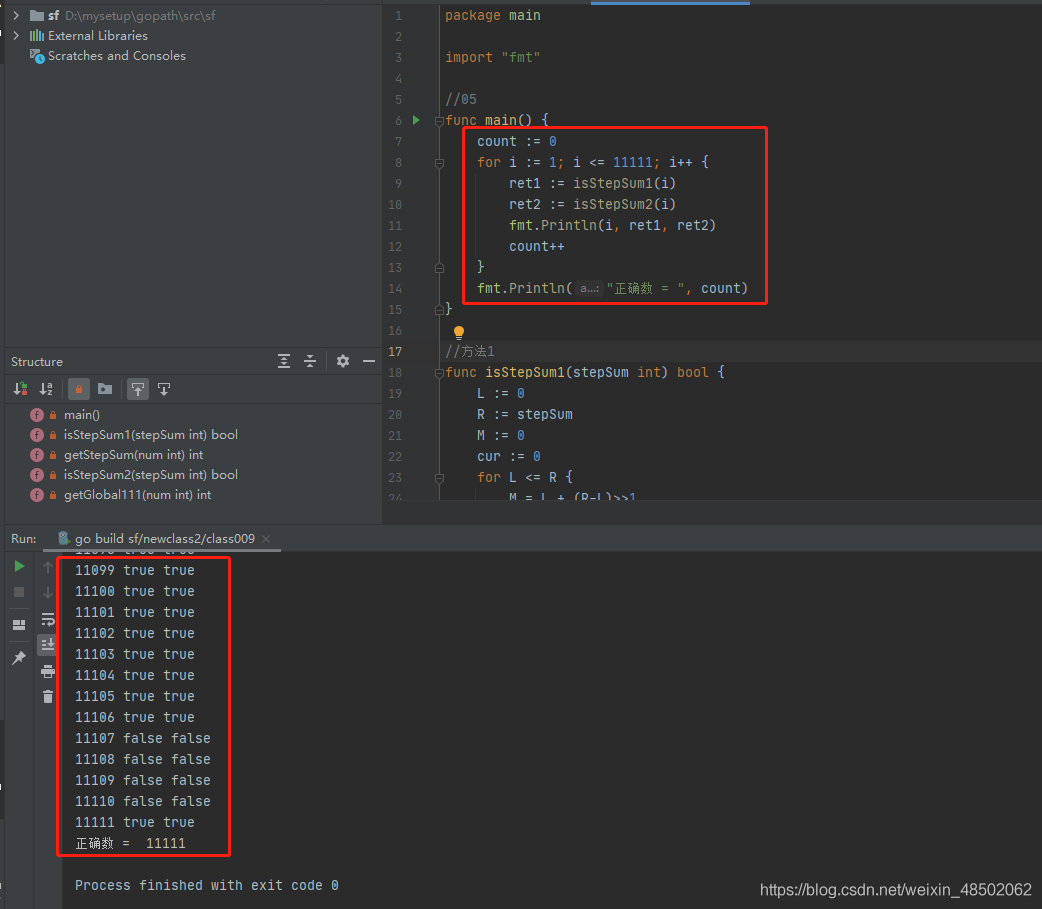
左神 java 代码

clear,cumsum,sum,numel,double,zeros,ones,abs,histeq,max/min
一. clear
clear意思是清空内存中的矩阵常量和变量,清除变量。每次在编写matlab程序时在开始最好加上clear。
二. cumsum
matlab中使用sum和cumsum两个加和函数,区别与联系参考matlab中cumsum函数详解。
matlab中cumsum函数通常用于计算一个数组各行的累加值。在matlab的命令窗口中输入doc cumsum或者help cumsum即可获得该函数的帮助信息。
调用格式及说明
matlab中cumsum函数通常用于计算一个数组各行的累加值。在matlab的命令窗口中输入doc cumsum或者help cumsum即可获得该函数的帮助信息。
调用格式及说明
格式一:B = cumsum(A)
这种用法返回数组不同维数的累加和。
为了便于接下来的叙述,解释一下matlab中矩阵、数组、向量的概念:[1]
首先,matlab是矩阵实验室的意思。也就是说matlab中的数据都被视为矩阵。
数组就是一个一行n列的矩阵,向量就是一个n行一列的矩阵。
如果A是一个向量,cumsum(A) 返回一个向量,该向量中第m行的元素是A中第1行到第m行的所有元素累加和;
如果A是一个矩阵,cumsum(A) 返回一个和A同行同列的矩阵,矩阵中第m行第n列元素是A中第1行到第m行的所有第n列元素的累加和;
如果A是一个多维数组,cumsum(A)只对A中第一个非奇异维进行计算。
格式二:B = cumsum(A, dim)
这种调用格式返回A中由标量dim所指定的维数的累加和。
例如:cumsum(A, 1)返回的是沿着第一维(各列)的累加和,cumsum(A, 2)返回的是沿着第二维(各行)的累加和。
具体用法参考程序示例或matlab的帮助文档。
相关函数
cumprod, prod, sum
编辑本段程序示例
% cumsum example
clc
clear
A=[1;2;3;4;5];
cumsum(A) % A是一个向量
B=1:5;
cumsum(B) % A是一个数组
C = [1 2 3; 4 5 6];
cumsum(C, 1)
cumsum(C,2)
% 构造一个多维数组
D = zeros(3, 3, 3);
D(:,:,2) = [1,2,3;4,5,6;7,8,9];
D(:,:,3) = ones(3,3)
cumsum(D)
三. sum
sum 函数的例子
a1=[1, 2, 3; 4, 5, 6; 7, 8, 10]
sum(a1)= 12 15 19
b=[1, 2, 3]
sum(b) = 6
c=[1, 2, 3]
sum(c)=6
四. numel
numel:元素总数。n=numel(A)该语句返回数组中元素的总数。
五. double
double(A);%返回与A矩阵数值相同但类型为double的矩阵。
六. zeros
zeros函数——生成零矩阵。
B = zeros(n):生成n×n全零阵。
B = zeros(m, n):生成m×n全零阵。
B = zeros([m n]):生成m×n全零阵。
B = zeros(d1, d2, d3……):生成d1×d2×d3×……全零阵或数组。
B = zeros([d1 d2 d3……]):生成d1×d2×d3×……全零阵或数组。
B = zeros(size(A)):生成与矩阵A相同大小的全零阵。
七. ones
ones的使用方法与zeros的使用方法类似。
八. abs
取绝对值。
九. imhist
功能:
计算和显示图像的色彩直方图
格式:
imhist(I, n)
imhist(X, map)
说明:
imhist(I, n)其中,n为指定的灰度级数目,缺省值为256。
imhist(X, map)就算和显示索引色图像X的直方图,map为调色板。
用astem(x, counts)同样可以显示直方图。
十. histeq
histeq函数
功能:
直方图均衡化
格式:
J = histeq(I, hgram)
J = histeq(I, n)
[J,T] = histeq(I, ...)
newmap = histeq(X, map, hgram)
newmap = histeq(X, map)
[new, T] = histeq(X, ...)
说明:
J = histeq(I, hgram)实现了所谓“直方图规定化”,即将原图象I的直方图变换成用户指定的向量hgram。hgram中的每一个元素都在[0,1]中;
J = histeq(I, n)指定均衡化后的灰度级数n,缺省值为64;
[J, T] = histeq(I, ...)返回从能将图像I的灰度直方图变换成图像J的直方图的变换T;
newmap = histeq(X, map)和[new, T] = histeq(X, ...)是针对索引色图像调色板的直方图均衡。
十一. max/min
求矩阵的最大值和最小值。
求矩阵A的最大值的函数有3种调用格式,分别是:
(1) max(A):返回一个行向量,向量的第i个元素是矩阵A的第i列上的最大值。
(2) [Y,U] = max(A):返回行向量Y和U,Y向量记录A的每列的最大值,U向量记录每列最大值的行号。
(3) max(A, [], dim):dim取1或2。dim取1时,该函数和max(A)完全相同;dim取2时,该函数返回一个列向量,其第i个元素是A矩阵的第i行上的最大值。
求最小值的函数是min,其用法和max完全相同。

Cumsum 基于列的条件,更改条件再次开始 cumsum
如何解决Cumsum 基于列的条件,更改条件再次开始 cumsum
我有这个数据集,我想根据状态找到 difftime 的总和,所需的输出是“outputcumsum”
x Status difftime outputcumsum24/11/2020 15:59:22 A 0 024/11/2020 16:29:22 A 0.5 0.525/11/2020 08:02:36 B 15,5538888888889 15,553888888888926/11/2020 08:45:30 B 24,715 40,268888888926/11/2020 09:15:59 A 0,508055555555556 0,50805555555555626/11/2020 09:45:59 A 0,5 1,00805555556
我试过了,但没有用
Data%>%group_by(Status)%>%summarise(outputcumsum=cumsum(difftime))
它给了我这个而不是我想要的
x Status difftime outputcumsum24/11/2020 15:59:22 A 0 024/11/2020 16:29:22 A 0.5 0.525/11/2020 08:02:36 B 15,553888888888926/11/2020 08:45:30 B 24,268888888926/11/2020 09:15:59 A 0,508055555555556 1,0080555555626/11/2020 09:45:59 A 0,50805555556
你知道有什么解决办法吗?
解决方法
您可以使用基本 R 的 rle() 如下
,
Data$outputcumsum <- ave(Data$difftime,with(rle(Data$Status),rep(1:length(values),lengths)),FUN = cumsum)
在 rleid 中使用 data.table 中的 group_by :
library(dplyr)library(data.table)Data%>%group_by(grp = rleid(Status)) %>%mutate(outputcumsum = cumsum(difftime))
或者在 data.table 本身中做任何事情。
,
library(data.table)setDT(Data)[,outputcumsum := cumsum(difftime),rleid(Status)]
带有 dplyr 的选项
library(dplyr)Data %>%group_by(grp = with(rle(Status),rep(seq_along(values),lengths))) %>%mutate(outputcumsum = cumsum(difftime))

cumsum累计函数系列:pd.cumsum()、pd.cumprod()、pd.cummax()、pd.cummin()
cum系列函数是作为DataFrame或Series对象的方法出现的,因此命令格式为D.cumsum()

举例:
D=pd.Series(range(0,5))
1. cumsum

2. cumprod

3. cummax

4. cummin

参考文献:
【1】Pandas —— cum累积计算和rolling滚动计算
关于numpy.sum 和 numpy.cumsum 之间的不同表现是什么?和numpy.sum()的使用的问题就给大家分享到这里,感谢你花时间阅读本站内容,更多关于2021-05-27:定义何为 step sum?比如 680,680+68+6=754,680 的 step sum 叫 754。、clear,cumsum,sum,numel,double,zeros,ones,abs,histeq,max/min、Cumsum 基于列的条件,更改条件再次开始 cumsum、cumsum累计函数系列:pd.cumsum()、pd.cumprod()、pd.cummax()、pd.cummin()等相关知识的信息别忘了在本站进行查找喔。
本文标签:





