Sybase IQ：在 Sybase IQ 中是否存在类似于 ROW CHANGE (DB2)/ORA_ROWSCN (Oracle) 的函数？

25-04-24 1

如果您想了解SybaseIQ：在SybaseIQ中是否存在类似于ROWCHANGE(DB2)/ORA_ROWSCN(Oracle)的函数？的知识，那么本篇文章将是您的不二之选。同时我们将深入剖析$ro

如果您想了解Sybase IQ：在 Sybase IQ 中是否存在类似于 ROW CHANGE (DB2)/ORA_ROWSCN (Oracle) 的函数？的知识，那么本篇文章将是您的不二之选。同时我们将深入剖析$row = $this->m_childlist[$i]->display($row, $sublist); 这是什么意思？该怎么解决、2023-04-14：n对情侣坐在连续排列的 2n 个座位上，想要牵到对方的手，人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的ID，情侣们按顺序编号，第一对、2023-06-06：给你二叉树的根结点 root ，请你设计算法计算二叉树的垂序遍历序列。对位于 (row, col) 的每个结点而言，其左右子结点分别位于 (row + 1, col -、Batch update returned unexpected row count from update: 0 actual row count: 0 expected: 1的各个方面，并给出实际的案例分析，希望能帮助到您！

本文目录一览：

Sybase IQ：在 Sybase IQ 中是否存在类似于 ROW CHANGE (DB2)/ORA_ROWSCN (Oracle) 的函数？
$row = $this->m_childlist[$i]->display($row, $sublist); 这是什么意思？该怎么解决
2023-04-14：n对情侣坐在连续排列的 2n 个座位上，想要牵到对方的手，人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的ID，情侣们按顺序编号，第一对
2023-06-06：给你二叉树的根结点 root ，请你设计算法计算二叉树的垂序遍历序列。对位于 (row, col) 的每个结点而言，其左右子结点分别位于 (row + 1, col -
Batch update returned unexpected row count from update: 0 actual row count: 0 expected: 1

Sybase IQ：在 Sybase IQ 中是否存在类似于 ROW CHANGE (DB2)/ORA_ROWSCN (Oracle) 的函数？

如何解决Sybase IQ：在 Sybase IQ 中是否存在类似于 ROW CHANGE (DB2)/ORA_ROWSCN (Oracle) 的函数？

我正在尝试从 Sybase IQ 数据库加载数据。为了避免在每次每日加载时完全加载，我更希望数据库中存在用于跟踪对行的最后更改的固有标记或时间戳。在 DB2 中，此函数称为 ROW CHANGE (https://www.ibm.com/docs/en/db2-big-sql/5.0.1?topic=expressions-row-change-expression)，在 Oracle (https://docs.oracle.com/database/121/SQLRF/pseudocolumns007.htm#SQLRF50953) 中称为。

它需要允许我只加载时间戳晚或令牌大于上次更改的数据。有谁知道 Sybase IQ 有这个功能吗？

提前致谢。

基里

$row = $this->m_childlist[$i]->display($row, $sublist); 这是什么意思？该怎么解决

$row = $this->m_childlist[$i]->display($row, $sublist); 这是什么意思？
全部代码在这里http://bbs.csdn.net/topics/390805879

下面这一句：

<br /><br />function display($row, $sublist)<br />{<br />  //this is code<br />$row = $this->m_childlist[$i]->display($row, $sublist);   //这一句是什么意思？？请指点<br />}<br />

登录后复制

------解决方案--------------------
$this->m_childlist[$i] 是一个 treenode 对象，另贴1段46行：
$this->m_childlist[$count]= new treenode($row[''postid''],$row[''title''],....

$row = $this->m_childlist[$i]->display($row, $sublist);
的作用是沿着树枝输出所有节点和叶子
------解决方案--------------------
看方法应该是递归遍历树节点。

2023-04-14：n对情侣坐在连续排列的 2n 个座位上，想要牵到对方的手，人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的ID，情侣们按顺序编号，第一对

2023-04-14：n对情侣坐在连续排列的 2n 个座位上，想要牵到对方的手，人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的ID，情侣们按顺序编号，第一对

2023-04-14：n对情侣坐在连续排列的 2n 个座位上，想要牵到对方的手，人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的ID，情侣们按顺序编号，第一对是 (0, 1)，第二对是 (2, 3)，以此类推，最后一对是 (2n-2, 2n-1)。返回最少交换座位的次数，以便每对情侣可以并肩坐在一起。每次交换可选择任意两人，让他们站起来交换座位。输入: row = [0,2,1,3]。输出: 1。输入: row = [3,2,0,1]。输出: 0。

答案2023-04-14：

大体过程如下：

定义并查集结构体 UnionFind，包括父节点数组 father、子树大小数组 size、辅助数组 help 和当前连通分量数 sets。
实现并查集结构体的三个方法：

a. 初始化方法 new，初始化父节点数组和子树大小数组，并将父节点数组的值初始化为自身，连通分量数初始为节点数量。

b. 查找方法 find，通过不断向上寻找父节点，直到找到根节点，并压缩路径优化查找效率。

c. 合并方法 union，找到 i 和 j 所在的连通分量的代表元素 fi 和 fj，以子树大小来优化合并操作，并更新连通分量数。
实现计算最少交换座位次数的函数 min_swaps_couples，首先获取座位数量 n，然后初始化并查集 uf，遍历相邻的座位，将情侣所在的连通分量合并。最后返回需要交换座位的最小次数。
在 main 函数中分别调用 min_swaps_couples 函数，传入测试数据，并输出最少交换座位的次数。
根据测试数据 row = [0, 2, 1, 3]，第一对情侣坐在座位0和1上，第二对情侣坐在座位2和3上，因此已经满足牵手的条件。而在测试数据 row = [3, 2, 0, 1] 中，第一对情侣坐在座位3和2上，第二对情侣坐在座位0和1上，因此需要交换他们的座位才能满足牵手的条件。

并查集的初始化时间复杂度为O(n)，其中n为节点数量。在计算最少交换座位次数的函数 min_swaps_couples 中，遍历相邻的座位需要O(n) 的时间，每次调用并查集中的 find 方法和 union 方法的时间复杂度均为O(α(n))，其中α(n) 是阿克曼函数的反函数，它比对数函数增长得慢，可以近似看作常数级别。因此，总时间复杂度为O(nα(n))。

空间复杂度取决于节点数量，需要使用O(n) 的空间存储父节点数组、子树大小数组和辅助数组。

rust代码如下：

// 定义并查集结构体
struct UnionFind {
    father: Vec<i32>, // 父节点数组
    size: Vec<i32>,   // 子树大小数组
    help: Vec<i32>,   // 辅助数组，用于优化路径压缩操作
    sets: i32,        // 当前连通分量数
}

impl UnionFind {
    // 初始化并查集
    fn new(n: i32) -> Self {
        let mut father = vec![0; n as usize]; // 初始化父节点数组
        let size = vec![1; n as usize]; // 初始化子树大小数组
        for i in 0..n {
            father[i as usize] = i; // 父节点初始化为自身
        }
        UnionFind {
            father, // 返回新建的并查集结构体
            size,
            help: vec![0; n as usize],
            sets: n, // 初始时连通分量数为n
        }
    }

    // 查找i所在连通分量的代表元素
    fn find(&mut self, mut i: i32) -> i32 {
        let mut hi = 0;
        while i != self.father[i as usize] {
            // 不断向上寻找父节点，直到找到根节点
            self.help[hi] = i; // 将当前节点压入辅助数组中
            hi += 1;
            i = self.father[i as usize]; // 向上跳一步
        }
        for j in (0..hi).rev() {
            // 压缩路径
            self.father[self.help[j] as usize] = i; // 将辅助数组中的节点的父节点设为根节点
        }
        i // 返回根节点
    }

    // 合并i和j所在的连通分量
    fn union(&mut self, i: i32, j: i32) {
        let fi = self.find(i); // 找到i的代表元素
        let fj = self.find(j); // 找到j的代表元素
        if fi != fj {
            // 如果i和j不在同一个连通分量中
            if self.size[fi as usize] >= self.size[fj as usize] {
                // 以树的大小来优化合并操作
                self.father[fj as usize] = fi; // 将fj的父节点设为fi
                self.size[fi as usize] += self.size[fj as usize]; // 更新fi子树的大小
            } else {
                self.father[fi as usize] = fj; // 将fi的父节点设为fj
                self.size[fj as usize] += self.size[fi as usize]; // 更新fj子树的大小
            }
            self.sets -= 1; // 连通分量数减1
        }
    }

    // 获取当前连通分量数
    fn sets(&self) -> i32 {
        self.sets
    }
}

// 计算最少交换座位的次数
fn min_swaps_couples(row: Vec<i32>) -> i32 {
    let n = row.len() as i32; // 座位数量
    let mut uf = UnionFind::new(n / 2); // 初始化并查集
    for i in (0..n).step_by(2) {
        // 遍历相邻的座位
        uf.union(row[i as usize] / 2, row[(i + 1) as usize] / 2); // 合并情侣所在的连通分量
    }
    n / 2 - uf.sets() // 返回需要交换座位的最小次数
}

fn main() {
    let row = vec![0, 2, 1, 3];
    let swaps = min_swaps_couples(row);
    println!("Minimum swaps required: {}", swaps); // Output: Minimum swaps required: 1

    let row = vec![3, 2, 0, 1];
    let swaps = min_swaps_couples(row);
    println!("Minimum swaps required: {}", swaps); // Output: Minimum swaps required: 0
}

2023-06-06：给你二叉树的根结点 root ，请你设计算法计算二叉树的垂序遍历序列。对位于 (row, col) 的每个结点而言，其左右子结点分别位于 (row + 1, col -

2023-06-06：给你二叉树的根结点 root ，请你设计算法计算二叉树的垂序遍历序列。

对位于 (row, col) 的每个结点而言，

其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1)

树的根结点位于 (0, 0) 。

二叉树的垂序遍历从最左边的列开始直到最右边的列结束，按列索引每一列上的所有结点，

形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点，

则按结点的值从小到大进行排序。

返回二叉树的垂序遍历序列。

输入：root = [3,9,20,null,null,15,7]。

输出：[[9],[3,15],[20],[7]]。

答案 2023-06-06：

大体过程如下：

1 定义结构体 TreeNode 表示二叉树节点，包含属性 Val 表示节点值和 Left 和 Right 分别表示左右节点。

2. 定义结构体 Info 表示节点信息，包含属性 row、col 和 val 分别表示节点所在的行、列和值。

3. 定义函数 NewInfo() 创建节点信息。

4. 定义切片类型 ByColThenRowThenVal 并实现其三个方法 Len()、Less() 和 Swap() 使之按列、行和节点值排序。

5. 定义函数 verticalTraversal() 实现二叉树的垂序遍历。

6. 在 verticalTraversal() 中，创建切片 collects 存储各节点信息，并将根节点的信息存入其中。

7. 调用函数 dfs() 遍历整个二叉树，添加各节点的信息到 collects 中。

8. 对 collects 按列、行和节点值排序。

9. 遍历 collects，将同列的所有节点值存入一个新的子切片，将子切片添加到答案 ans 中。

10. 返回答案 ans。

时间复杂度是 O (nlogn)，其中 n 是节点数。n 个节点需要遍历一次，排序时间复杂度是 O (nlogn)。所以总时间复杂度是 O (nlogn)。

空间复杂度是 O (n)，其中 n 是节点数。需要使用切片 collects 来存储节点的信息，collects 的长度最大是 n，所以空间复杂度是 O (n)。

golang 完整代码如下：

package main

import (
	"fmt"
	"sort"
)

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

type Info struct {
	row int
	col int
	val int
}

func NewInfo(r, c, v int) Info {
	return Info{row: r, col: c, val: v}
}

type ByColThenRowThenVal []Info

func (bc ByColThenRowThenVal) Len() int { return len(bc) }

func (bc ByColThenRowThenVal) Less(i int, j int) bool {
	if bc[i].col != bc[j].col {
		return bc[i].col < bc[j].col
	}
	if bc[i].row != bc[j].row {
		return bc[i].row < bc[j].row
	}
	return bc[i].val < bc[j].val
}

func (bc ByColThenRowThenVal) Swap(i int, j int) { bc[i], bc[j] = bc[j], bc[i] }

func verticalTraversal(root *TreeNode) [][]int {
	collects := make([]Info, 0, 1000)
	rootInfo := NewInfo(0, 0, root.Val)
	collects = append(collects, rootInfo)
	dfs(root, rootInfo, &collects)
	sort.Sort(ByColThenRowThenVal(collects))
	ans := make([][]int, 0, 1000)
	for i := 0; i < len(collects); i++ {
		if i == 0 || collects[i-1].col != collects[i].col {
			ans = append(ans, []int{})
		}
		ans[len(ans)-1] = append(ans[len(ans)-1], collects[i].val)
	}
	return ans
}

func dfs(root *TreeNode, rootInfo Info, collects *[]Info) {
	if root.Left != nil {
		leftInfo := NewInfo(rootInfo.row+1, rootInfo.col-1, root.Left.Val)
		*collects = append(*collects, leftInfo)
		dfs(root.Left, leftInfo, collects)
	}
	if root.Right != nil {
		rightInfo := NewInfo(rootInfo.row+1, rootInfo.col+1, root.Right.Val)
		*collects = append(*collects, rightInfo)
		dfs(root.Right, rightInfo, collects)
	}
}

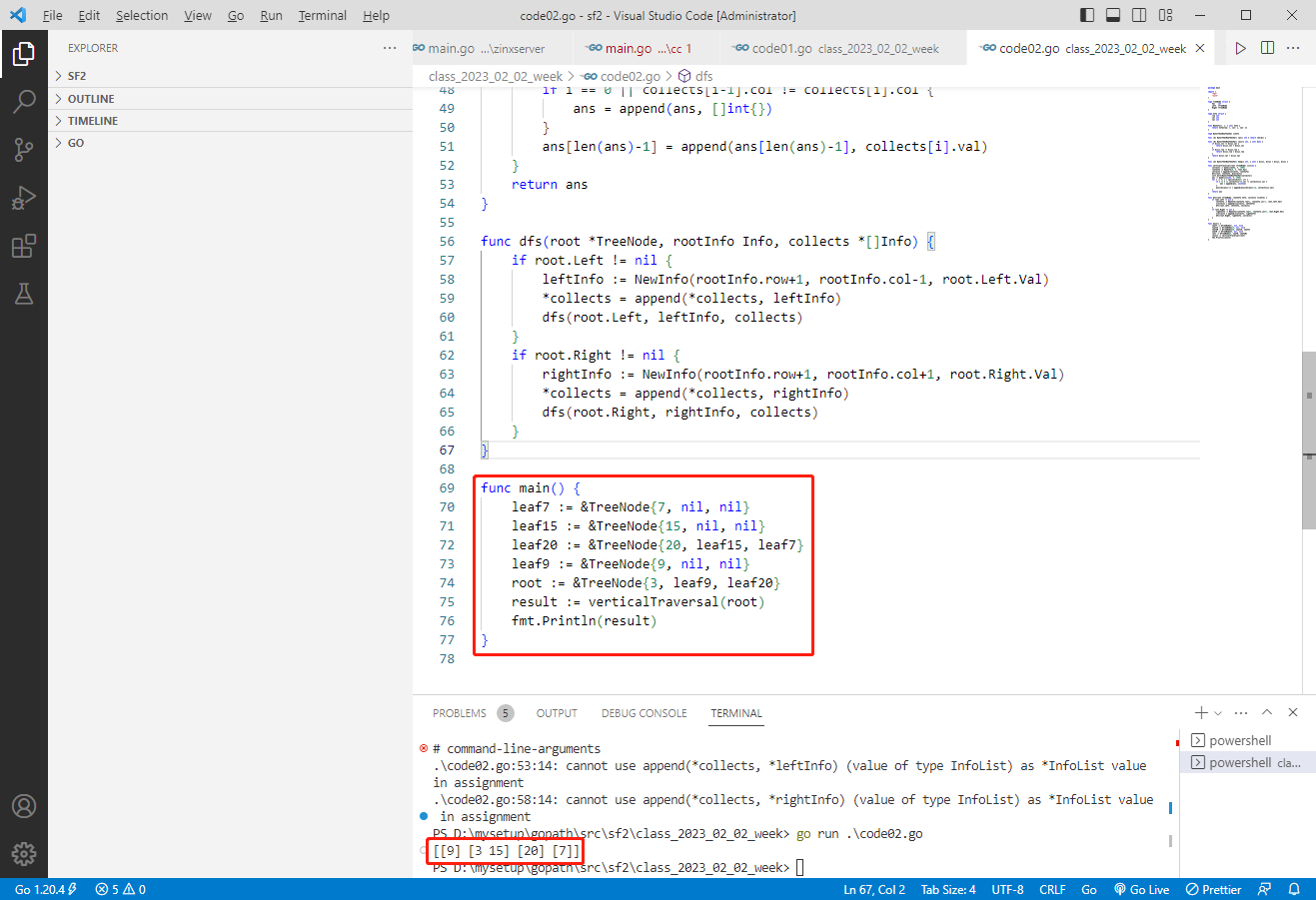
func main() {
	leaf7 := &TreeNode{7, nil, nil}
	leaf15 := &TreeNode{15, nil, nil}
	leaf20 := &TreeNode{20, leaf15, leaf7}
	leaf9 := &TreeNode{9, nil, nil}
	root := &TreeNode{3, leaf9, leaf20}
	result := verticalTraversal(root)
	fmt.Println(result)
}

在这里插入图片描述

c++ 完整代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

struct Info {
    int row;
    int col;
    int val;
    Info(int r, int c, int v) {
        row = r;
        col = c;
        val = v;
    }
};

struct InfoComparator {
    bool operator() (const Info& o1, const Info& o2) {
        if (o1.col != o2.col) {
            return o1.col < o2.col;
        }
        if (o1.row != o2.row) {
            return o1.row < o2.row;
        }
        return o1.val < o2.val;
    }
};

void dfs(TreeNode* root, Info rootInfo, vector<Info>& collects) {
    if (root->left != nullptr) {
        Info leftInfo(rootInfo.row + 1, rootInfo.col - 1, root->left->val);
        collects.push_back(leftInfo);
        dfs(root->left, leftInfo, collects);
    }
    if (root->right != nullptr) {
        Info rightInfo(rootInfo.row + 1, rootInfo.col + 1, root->right->val);
        collects.push_back(rightInfo);
        dfs(root->right, rightInfo, collects);
    }
}

vector<vector<int>> verticalTraversal(TreeNode* root) {
    vector<Info> collects;
    Info rootInfo(0, 0, root->val);
    collects.push_back(rootInfo);
    dfs(root, rootInfo, collects);
    sort(collects.begin(), collects.end(), InfoComparator());
    vector<vector<int>> ans;
    for (int i = 0; i < collects.size(); i++) {
        if (i == 0 || collects[i - 1].col != collects[i].col) {
            ans.push_back(vector<int>());
        }
        ans.back().push_back(collects[i].val);
    }
    return ans;
}

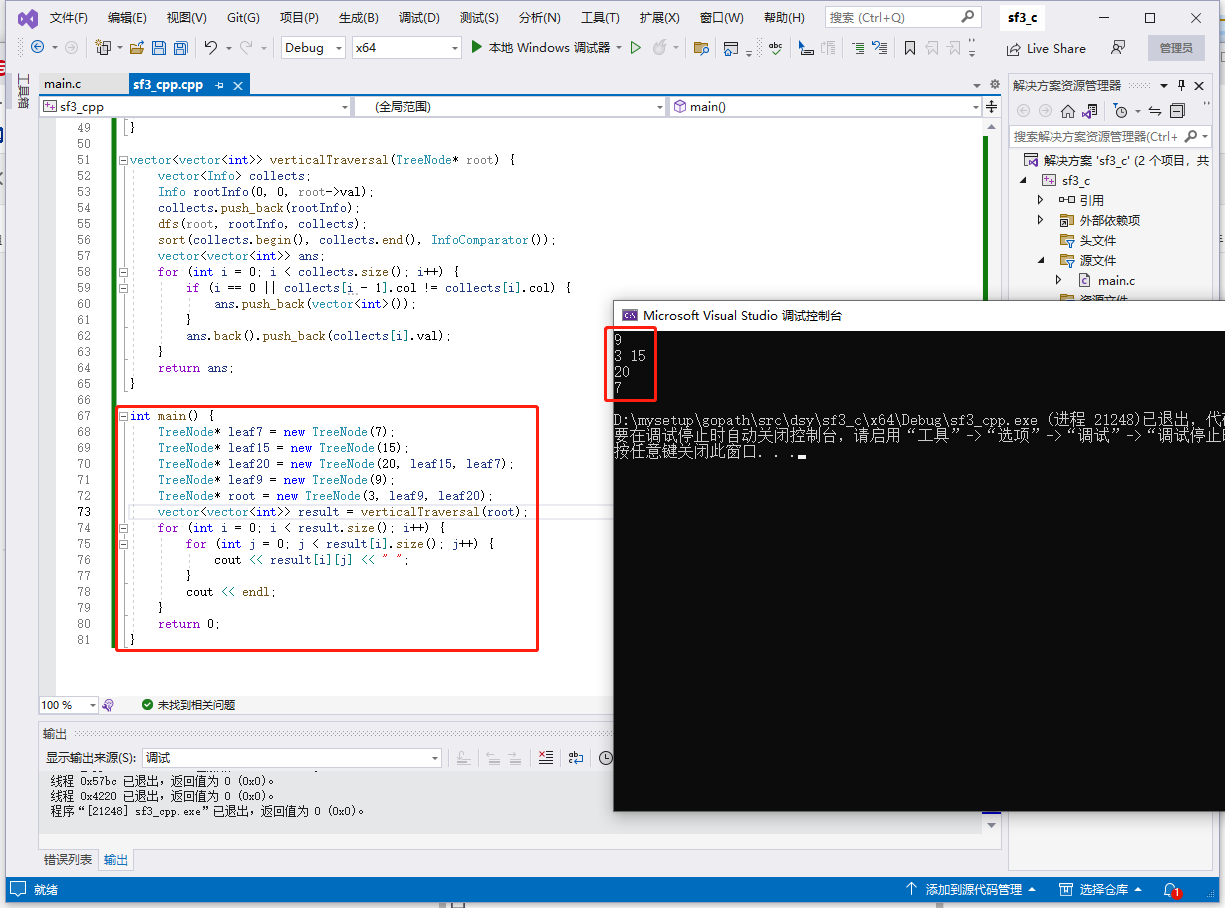
int main() {
    TreeNode* leaf7 = new TreeNode(7);
    TreeNode* leaf15 = new TreeNode(15);
    TreeNode* leaf20 = new TreeNode(20, leaf15, leaf7);
    TreeNode* leaf9 = new TreeNode(9);
    TreeNode* root = new TreeNode(3, leaf9, leaf20);
    vector<vector<int>> result = verticalTraversal(root);
    for (int i = 0; i < result.size(); i++) {
        for (int j = 0; j < result[i].size(); j++) {
            cout << result[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

在这里插入图片描述

Batch update returned unexpected row count from update: 0 actual row count: 0 expected: 1

@OneToMany 单向时，保存主体时，出现异常：

Batch update returned unexpected row count from update: 0 actual row count: 0 expected: 1

@OneToMany(fetch=FetchType.EAGER)
@JoinColumn(name="ztid",updatable=false,insertable=false)  
private List<SlrZttp> slrZttps;
public String getZtid(){
    return ztid;
}

并不希望保存从体。

插入 updateble,insertable 异常解决。

今天关于Sybase IQ：在 Sybase IQ 中是否存在类似于 ROW CHANGE (DB2)/ORA_ROWSCN (Oracle) 的函数？的分享就到这里，希望大家有所收获，若想了解更多关于$row = $this->m_childlist[$i]->display($row, $sublist); 这是什么意思？该怎么解决、2023-04-14：n对情侣坐在连续排列的 2n 个座位上，想要牵到对方的手，人和座位由一个整数数组 row 表示，其中 row[i] 是坐在第 i 个座位上的人的ID，情侣们按顺序编号，第一对、2023-06-06：给你二叉树的根结点 root ，请你设计算法计算二叉树的垂序遍历序列。对位于 (row, col) 的每个结点而言，其左右子结点分别位于 (row + 1, col -、Batch update returned unexpected row count from update: 0 actual row count: 0 expected: 1等相关知识，可以在本站进行查询。

本文标签：