GVKun编程网logo

leetcode 437. Path Sum III 路径总和 III(中等)（leetcode路径数）

19

在这篇文章中，我们将为您详细介绍leetcode437.PathSumIII路径总和III(中等)的内容，并且讨论关于leetcode路径数的相关问题。此外，我们还会涉及一些关于437.PathSum

在这篇文章中，我们将为您详细介绍leetcode 437. Path Sum III 路径总和 III(中等)的内容，并且讨论关于leetcode路径数的相关问题。此外，我们还会涉及一些关于437. Path Sum III - Easy、437. 路径总和 III、Combination Sum I & II & IIIleetcode、Leetcode - Combination Sum I，II，III的知识，以帮助您更全面地了解这个主题。

本文目录一览：

leetcode 437. Path Sum III 路径总和 III(中等)（leetcode路径数）

leetcode 437. Path Sum III 路径总和 III(中等)（leetcode路径数）

一、题目大意

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

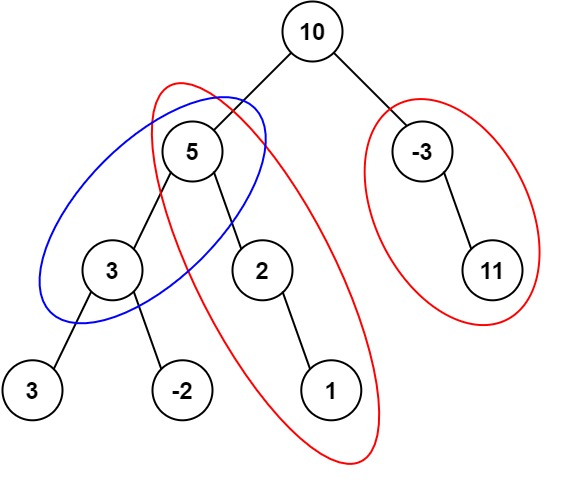
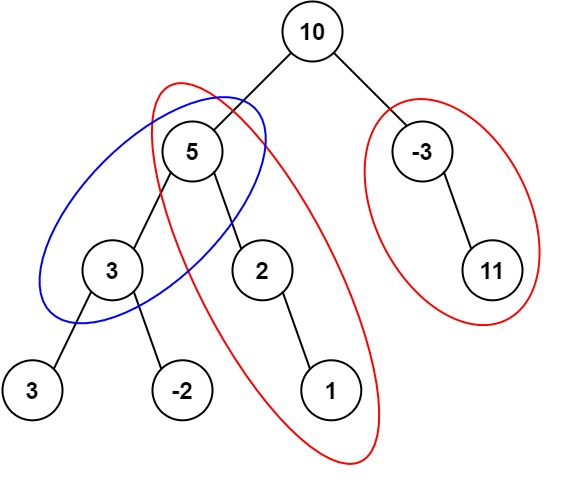
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出：3 解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出：3

提示:

  • 二叉树的节点个数的范围是 [0,1000]

  • -109 <= Node.val <= 109

  • -1000 <= targetSum <= 1000

二、解题思路

双层递归实现，注意分情况考虑：1、如果选取该节点加入路径，则之后必须继续加入连续节点，或停止加入节点；2、如果不选取该节点加入路径，则对其左右节点进行重新考虑。因此一个方便的方法是我们创建一个辅函数，专门用来计算连续加入节点的路径。

三、解题方法

3.1 Java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return 0;
        }
        return pathSumStartWithRoot(root, targetSum) + pathSum(root.left, targetSum) + pathSum(root.right, targetSum);
    }

    /**
     * 注意，这里入参类型为long，否则通不过下面这个用例
     * 这里root.val太大，递归调用多了targetNum-root.val就会溢出整数型的最小值，把参数换成long即可
     * [1000000000,1000000000,null,294967296,null,1000000000,null,1000000000,null,1000000000]
     * 0
     */
    int pathSumStartWithRoot(TreeNode root, long targetSum) {
        if (root == null) {
            return 0;
        }

        int count = root.val == targetSum ? 1 : 0;
        count += pathSumStartWithRoot(root.left, targetSum - root.val);
        count += pathSumStartWithRoot(root.right, targetSum - root.val);
        return count;
    }
}

四、总结小记

  • 2022/9/8 求人不如求己

437. Path Sum III - Easy

437. Path Sum III - Easy

You are given a binary tree in which each node contains an integer value.

Find the number of paths that sum to a given value.

The path does not need to start or end at the root or a leaf,but it must go downwards (traveling only from parent nodes to child nodes).

The tree has no more than 1,000 nodes and the values are in the range -1,000,000 to 1,000.

Example:

root = [10,5,-3,3,2,null,11,-2,1],sum = 8

      10
     /      5   -3
   / \      3   2   11
 / \   3  -2   1

Return 3. The paths that sum to 8 are:

1.  5 -> 3
2.  5 -> 2 -> 1
3. -3 -> 11

 

注意一下这里的路径不是从root到leaf，中间有部分的路径加和为sum也可

time: O(n),space: O(height)

/**
 * DeFinition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int pathSum(TreeNode root,int sum) {
        if(root == null) {
            return 0;
        }
        return dfs(root,sum) + pathSum(root.left,sum) + pathSum(root.right,sum);
    }
    
    public int dfs(TreeNode root,int sum) {
        if(root == null) {
            return 0;
        }
        int cnt = 0;
        if(root.val == sum) {
            cnt++;
        }
        cnt += dfs(root.left,sum - root.val);
        cnt += dfs(root.right,sum - root.val);
        return cnt;
    }
}

437. 路径总和 III

437. 路径总和 III

https://leetcode-cn.com/problems/pa-sum-iii/

使用语言 Golang

先上正确的解决方案：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sumChild(root *TreeNode, sum int) int {
    if root == nil {
        return 0
    }
    
    r := 0
    if root.Val == sum {
        r = 1
    }
    
    newSum := sum - root.Val
    return r + sumChild(root.Left, newSum) + sumChild(root.Right, newSum)
}
func pathSum(root *TreeNode, sum int) int {
    if root == nil {
        return 0
    }
    return sumChild(root, sum) + pathSum(root.Left, sum) + pathSum(root.Right, sum)
}

感悟：思路正确的程序，一定是最简洁直观的。

其实我最开始的思路就一直很正确，我把问题分解了一下，实际上就是求每个路径的和，其中和等于目标值的次数。下面是我第一次的提交：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sumChild(root *TreeNode, targetSum int, sum int) int {
        if root == nil {
        return 0
    }
    if root.Val == sum {
        return 1 + sumChild(root.Left, targetSum, targetSum) + sumChild(root.Right, targetSum, targetSum)
    } else if root.Val > sum {
        return 0 + sumChild(root.Left, targetSum, targetSum) + sumChild(root.Right, targetSum, targetSum)
    }
    
    newSum := sum - root.Val
    return sumChild(root.Left, targetSum, newSum) + sumChild(root.Right, targetSum, newSum) + sumChild(root.Left, targetSum, sum) + sumChild(root.Right, targetSum, sum)
}
func pathSum(root *TreeNode, sum int) int {
    return sumChild(root, sum, sum)
}

sumChild 的逻辑比较复杂，除了判断边界，我还判断了当前值与目标值的差异，这样其实是有问题的：并不是当前值比目标值大，就意味着整条路径都没有希望了。我也是在测试用例跑挂之后才想明白这个问题。

改了一版变成了这样：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sumChild(root *TreeNode, targetSum int, sum int) int {
    if root == nil {
        return 0
    }
    if root.Val == sum {
        return 1 + sumChild(root.Left, targetSum, targetSum) + sumChild(root.Right, targetSum, targetSum)
    }
    
    newSum := sum - root.Val
    return sumChild(root.Left, targetSum, newSum) + sumChild(root.Right, targetSum, newSum) + sumChild(root.Left, targetSum, targetSum) + sumChild(root.Right, targetSum, targetSum)
}
func pathSum(root *TreeNode, sum int) int {
    return sumChild(root, sum, sum)
}

这回只针对等值的情况做了处理，然而测试用例依然没跑过，挂在了下面这个输入上：

[1,null,2,null,3,null,4,null,5]
3

期望结果是 2，但是我跑出来是 3。想了想之后，我明白了：
我的程序中发生了重复遍历！

就是同一条路径，遍历了多次。

很明显，我为了确保能够遍历到每一条路径，在 sumChild 中故意留了一个 targetSum，并用这个 targetSum 向每个子树进行递归。但实际上 sumChild 自己也在递归。拿左子树举个例子，左子树用新值递归了一遍，又用真实的目标值递归了一遍，对于左子树的左子树来讲，他一定会被递归到两次。

我忽然意识到，targetSum 这样一个很变扭的东西或许本身就不该出现，当你觉得一个东西很变扭的时候，可能他真的有问题。思考之后，我把程序改成了这样：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sumChild(root *TreeNode, sum int) int {
    if root == nil {
        return 0
    }
    
    r := 0
    if root.Val == sum {
        r = 1
    }
    
    newSum := sum - root.Val
    return r + sumChild(root.Left, newSum) + sumChild(root.Right, newSum)
}
func pathSum(root *TreeNode, sum int) int {
    if root == nil {
        return 0
    }
    return sumChild(root, sum) + pathSum(root.Left, sum) + pathSum(root.Right, sum)
}

整个程序变的豁然开朗，pathSum 负责遍历每个子树，而 sumChild 负责计算子树上的可能路径的和。

很多时候 简洁 = 正确。

Combination Sum I & II & IIIleetcode

Combination Sum I & II & IIIleetcode

Combination Sum I

Given a set of candidate numbers (C) and a target number (T), find all
unique combinations in C where the candidate numbers sums to T.

The same repeated number may be chosen from C unlimited number of
times.

Note: All numbers (including target) will be positive integers.
Elements in a combination (a1, a2, … , ak) must be in non-descending
order. (ie, a1 ≤ a2 ≤ … ≤ ak). The solution set must not contain
duplicate combinations. For example, given candidate set 2,3,6,7 and
target 7, A solution set is: [7] [2, 2, 3]

回溯法

说明

做法是我们遍历所有的结果, 然后找出符合的答案. 每次遍历我们只找当前的数和后面的数来选取, 所以要先给数组排序.这样就不会漏下答案

复杂度

时间O(n!) 空间栈O(n)

代码

public List<List<Integer>> combinationSum(int[] candidates, int target) {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    if (candidates == null || candidates.length == 0 ) {
        return res;
    }
    Arrays.sort(candidates);
    List<Integer> tem = new ArrayList<Integer>();
    helper(res, tem, target, candidates, 0);
    return res;
}
public void helper(List<List<Integer>> res, List<Integer> tem, int target, int[] candidates, int pos) {
    if (target == 0) {
        res.add(new ArrayList<Integer>(tem));
        return;
    }
    if (target < 0) {
        return;
    }
    for (int i = pos; i < candidates.length; i++) {
        tem.add(candidates[i]);
        helper(res, tem, target - candidates[i], candidates, i);
        tem.remove(tem.size() - 1);
    }
}

Combination Sum II

Given a collection of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.

Each number in C may only be used once in the combination.

Note:
All numbers (including target) will be positive integers.
Elements in a combination (a1, a2, … , ak) must be in non-descending order. (ie, a1 ≤ a2 ≤ … ≤ ak).
The solution set must not contain duplicate combinations.
For example, given candidate set 10,1,2,7,6,1,5 and target 8, 
A solution set is: 
[1, 7] 
[1, 2, 5] 
[2, 6] 
[1, 1, 6]

回溯法

说明

类似subsetII, 对于递归过程中每次新选取的可以是和递归数组有相同的，但是后面的元素就不能相同了

复杂度

时间O(n!) 空间栈O(n)

代码

public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    if (candidates == null || candidates.length == 0 ) {
        return res;
    }
    Arrays.sort(candidates);
    List<Integer> tem = new ArrayList<Integer>();
    helper(res, tem, target, candidates, 0);
    return res;
}
public void helper(List<List<Integer>> res, List<Integer> tem, int target, int[] candidates, int pos) {
    if (target == 0) {
        res.add(new ArrayList<Integer>(tem));
        return;
    }
    if (target < 0) {
        return;
    }
    for (int i = pos; i < candidates.length; i++) {
        if (i != pos && candidates[i] == candidates[i - 1]) {
            continue;
        }
        tem.add(candidates[i]);
        helper(res, tem, target - candidates[i], candidates, i + 1);
        tem.remove(tem.size() - 1);
    }
}

Combination Sum III

Find all possible combinations of k numbers that add up to a number n,
given that only numbers from 1 to 9 can be used and each combination
should be a unique set of numbers.

Ensure that numbers within the set are sorted in ascending order.

Example 1:

Input: k = 3, n = 7

Output:

[[1,2,4]]

Example 2:

Input: k = 3, n = 9

Output:

[[1,2,6], [1,3,5], [2,3,4]]

回溯法

说明

这道题更加类似combinations那道题, 只是返回条件不仅仅是k数目相等, 递归得到的n也要相等才能返回.

代码

public List<List<Integer>> combinationSum3(int k, int n) {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    if (n <= 0 || k <= 0) {
        return res;
    }
    List<Integer> tem = new ArrayList<Integer>();
    helper(tem, res, 1, n, k);
    return res;
}
public void helper(List<Integer> tem, List<List<Integer>> res, int index, int n, int k) {
    if (tem.size() == k && n == 0) {
        res.add(new ArrayList<Integer>(tem));
        return;
    }
    if (tem.size() > k || n < 0) {
        return;
    }
    for (int i = index; i <= 9; i++) {
        tem.add(i);
        helper(tem, res, i + 1, n - i, k);
        tem.remove(tem.size() - 1);
    }
}

Leetcode - Combination Sum I，II，III

Leetcode - Combination Sum I，II，III

Leetcode Combination Sum I，II，III 均是dfs + backtraing 模板题目，适合集中练习

Leetcode - 039. Combination Sum

我的思路：
1.排序是必要的，为什么排序是必要的？考虑到我们dfs + backtraing 的标准三步(1.优先判定可行解 2.剪枝 3.遍历下行状态，更新backtracing的追踪变量)，我们如何判定是一个可行解，显然是当前sum = target，那么如果我们不排序的话当前sum > target 还有可能pop 最后一个元素然后与之后较小的元素形成可行解，这样带来了不必要的麻烦而且无法剪枝，所以我们应该排序原数组
2.遵循标准三步，注意是可重复的peek，那么每次的下行状态包括当前状态的终止位置

class Solution {
public:

    void dfs(vector<vector<int>> &vct, vector<int> &cur, vector<int>& nums,
        const int target, int cursum, int index)
    {
        if (cursum == target)
        {
            vct.push_back(cur);
            return;
        }
        int n = nums.size();
        if (cursum > target || index >= n)
            return;
        for (int i = index; i < n; ++i)
        {
            cur.push_back(nums[i]);
            dfs(vct, cur, nums, target, cursum + nums[i], i);
            cur.pop_back();
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> vct;
        vector<int> cur;
        if (candidates.size() <= 0)
            return vct;
        sort(candidates.begin(), candidates.end());
        dfs(vct, cur, candidates, target, 0, 0);
        return vct;
    }
};

Leetcode - 040. Combination Sum II

我的思路：
1.主体思路与Combination Sum 是一致的
2.有重复元素
3.元素只能使用一次
这里的去重操作需要技巧：
首先，每个元素(不管是否与其他元素相等)只能使用一次，可以用used数组标识
考虑到样例中给出的 1 + 1 + 6 = 8，不能单纯的后置元素等于前置元素去重，那我们考虑什么时候重复？
假设样本[1,1,1,3] , target = 5, 那么解为[1,1,3]
根据深搜的性质，一定是index = 0,1,3的元素组成了解，那么我们可以了解到的是，当元素存在前置等值元素且其前置等值元素还未被使用时就使用当前元素必然会发生重复解。了解这一点，稍作判断修改即可AC


class Solution {
public:

    void dfs(vector<vector<int>> &vct, vector<int> cur, vector<int>& nums, vector<int>& used,
        const int target, int cursum, int index)
    {
        if (cursum == target)
        {
            vct.push_back(cur);
            return;
        }
        int n = nums.size();
        if (cursum > target || index >= n)
            return;
        for (int i = index + 1; i < n; ++i)
        {
            int j = i - 1;
            int placable = 1;
            while (j >= 0 && nums[j] == nums[i])
            {
                if (used[i] == 0)
                {
                    placable = 0;
                    break;
                }
            }
            if (placable == 0)
                continue;
            used[i] = 1;
            cur.push_back(nums[i]);
            dfs(vct, cur, nums, used, target, cursum + nums[i], i + 1);
            cur.pop_back();
            used[i] = 0;
        }

    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<vector<int>> vct;
        vector<int> cur;
        int n = candidates.size();
        if (n <= 0)
            return vct;
        vector<int> used(n, 0);
        sort(candidates.begin(), candidates.end());
        dfs(vct, cur, candidates, used,target, 0, 0);
        return vct;
    }
};

Leetcode - 216. Combination Sum III

我的思路：
1.使用k个1 - 9之间的正整数组成target，主体思路同上
2.剪枝的时候多加一个当前解空间的大小判断一下即可，论起来比起Combination Sum II还要容易一些

class Solution {
public:

    void dfs(vector<vector<int>> &vct, vector<int> &cur, vector<int> &nums,
        int k, int n, int index, int cursum)
    {
        if (int(cur.size()) == k && cursum == n)
        {
            vct.push_back(cur);
            return;
        }
        // 注意这里可以取等和不能取等的
        if (int(cur.size()) >= k || cursum >= n || index > 9)
            return;
        for (int i = index; i <= 9; ++i)
        {
            cur.push_back(i);
            dfs(vct, cur, nums, k, n, i + 1, cursum + i);
            cur.pop_back();
        }
    }

    vector<vector<int>> combinationSum3(int k, int n) {
        vector<vector<int>> vct;
        vector<int> cur;
        vector<int> nums{ 0,1,2,3,4,5,6,7,8,9 };
        dfs(vct, cur, nums, k, n, 1, 0);
        return vct;
    }
};

今天的关于leetcode 437. Path Sum III 路径总和 III(中等)和leetcode路径数的分享已经结束，谢谢您的关注，如果想了解更多关于437. Path Sum III - Easy、437. 路径总和 III、Combination Sum I & II & IIIleetcode、Leetcode - Combination Sum I，II，III的相关知识，请在本站进行查询。

本文标签：

上一篇leetcode 101. Symmetric Tree 对称二叉树(简单)（对称的二叉树）

下一篇Docker搭建私有镜像仓库与WordPress（docker 搭建私有镜像仓库）

相关文章