GVKun编程网logo

Python中的动态时间规整（python动态数据）

21

在这篇文章中，我们将为您详细介绍Python中的动态时间规整的内容，并且讨论关于python动态数据的相关问题。此外，我们还会涉及一些关于DDTW导数动态时间规整算法、DTW动态时间规整算法、pyth

在这篇文章中，我们将为您详细介绍Python中的动态时间规整的内容，并且讨论关于python动态数据的相关问题。此外，我们还会涉及一些关于DDTW 导数动态时间规整算法、DTW动态时间规整算法、python – django中的动态数据库表、python+tkinter制作一个可自定义的动态时钟及详细解释，珍藏版的知识，以帮助您更全面地了解这个主题。

本文目录一览：

Python中的动态时间规整（python动态数据）

Python中的动态时间规整（python动态数据）

有人知道具有DTW实现的python库吗？mlpy似乎有我想要的东西，但我似乎无法正确安装它-
当前正在等待邮件列表中的答复，因此我认为我将扩大其他库的范围。

答案1

小编典典

作为记录，我已经能够使用R，R中的DTW和rpy2的混搭。在Python中使用R十分简单，并且大大扩展了python的统计功能。这是查找偏移噪声正弦和余弦序列之间的距离的示例：

    import rpy2.robjects as robjects    r = robjects.r    r(''library("dtw")'')    idx = r.seq(0,6.28,len=100)    template = r.cos(idx)    query = r.sin(idx)+r(''runif(100)/10'')    alignment=r.dtw(query,template,keep=r(''TRUE''))    robjects.globalenv["alignment"] =  alignment    dist = r(''alignment$distance'')    print(dist)

DDTW 导数动态时间规整算法

DDTW 导数动态时间规整算法

DDTW 导数动态时间规整算法

Derivative Dynamic Time Warping（DDTW） 是对 Dynamic Time Warping (DTW) 的一种改进。缓解了经典DTW算法所产生的“奇点”（Singularities）问题，本文将从以下几个方面介绍DDTW算法。

1、算法背景

时间序列是几乎每一个科学学科中普遍存在的数据形式。时间序列的常见处理任务是将一个序列与另一个序列进行比较，以比较两个时间序列的相似度。在某些领域，使用非常简单的距离度量（例如欧式距离）就足够了。

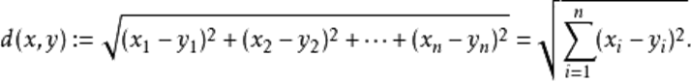image.png 但是，在大多情况下，两个序列的总体组成形状大致相同，但是这些形状在X轴上并不对齐。（图1）

为了找到这些序列之间的相似性，或作为对它们进行平均之前的预处理步骤，我们必须“扭曲”一个（或全部两个）序列的时间轴以实现更好的比对。动态时间规整（DTW）是一种有效实现这种规整的技术。

例如图A所示，实线和虚线分别是同一个词“pen”的两个语音波形（在y轴上拉开了，以便观察）。可以看到他们整体上的波形形状很相似，但在时间轴上却是不对齐的，假设一个序列中的第i个点与另一序列中的第i个点对齐将产生“悲观差异”（pessimistic dissimilarity）。而在图B中，DTW就可以通过找到这两个波形对齐的点，这样计算它们的距离才是正确的。 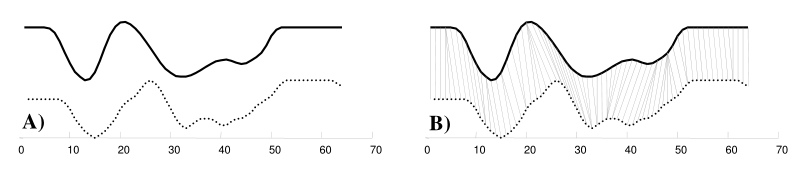image.png （图1） 因此，DTW显示出了很好的能力，除了在数据挖掘（Keogh＆Pazzani 2000，Yi et. al.1998，Berndt＆Clifford 1994）上的应用，DTW还被用于手势识别（Gavrila＆Davis 1995），机器人技术（Schmill et. al 1999），语音处理（Rabiner＆Juang 1993），制造业（Gollmer＆Posten 1995）和医药行业（Caiani et. al 1998）。

2、经典动态时间规整算法

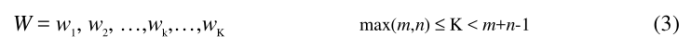假设我们有两个时间序列Q和C，长度分别为n和m，其中： image.png 为了对齐这两个序列，我们需要构造一个n x m的矩阵网格，矩阵元素(i, j)表示qi和cj两个点的距离d(qi, cj)（也就是序列Q的每一个点和C的每一个点之间的相似度，距离越小则相似度越高。这里先不管顺序），一般采用欧式距离。每一个矩阵元素(i, j)表示点qi和cj的对齐。有了这个矩阵，我们就能够对两个时间序列之间的距离进行计算，并显示出一条规整路径warping path（W）。由于有许多不同的对时间轴的“扭曲”方式，因此我们能够得到很多条规整路径（W的公式如下），但我们的目标是找到一条最短的规整路径，以判断两条时间序列之间的“距离”也就是相似度，而如何快速地找到这条路径呢？我们发现动态规划（Dynamic Programming）可以为我们提供很大的方便。 Dynamic Programming算法可以归结为寻找一条通过此网格中若干格点的路径，路径通过的格点即为两个序列进行计算的对齐的点。 image.png w的第i个元素为w=(i,j)定义了两条时间序列的映射。并且，规整路径一般受到以下几种约束条件。 1）边界条件：定义了规整路径必须在矩阵的对角元素中开始和结束； 2）连续性：这将规整路径中的允许步骤限制为相邻的单元（包括对角相邻的单元）； 3）单调性：这迫使W中的点在时间上单调进行。

结合连续性和单调性约束，每一个格点的路径就只有三个方向了。例如如果路径已经通过了格点(i, j)，那么下一个通过的格点只可能是下列三种情况之一：(i+1, j)，(i, j+1)或者(i+1, j+1)。 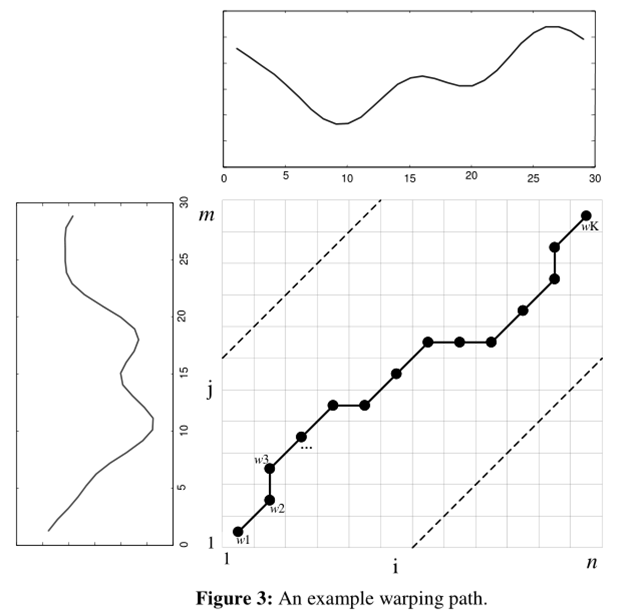image.png 由上文所述，我们可以通过比较满足以上条件所有规整路径找出最短的规整路径，但是DP为我们提供了一个更好地方法来计算最短路径。我们首先定义一个累积距离cumulative distance γ，累积距离γ(i,j)为当前格点距离d(i,j)，也就是点qi和cj的欧式距离与可以到达该点的最小的邻近元素的累积距离之和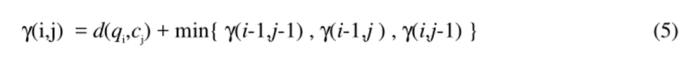： image.png 通过动态规划算法，我们可以较简单地得到最短的累积距离。

3、动态时间规划的“奇点”问题

DTW算法最重要的特征就是通过“扭曲”X轴来解释Y轴变量，以达到使时间序列对齐的目的。但是简单的通过Y轴的变量值来扭曲X轴会导致“不直观”（unintuitive）的对齐，其中一个时间序列上的单个点会映射到另一个时间序列的一部分上。我们称这种我们不期望看到的行为为“奇点”（singularities）。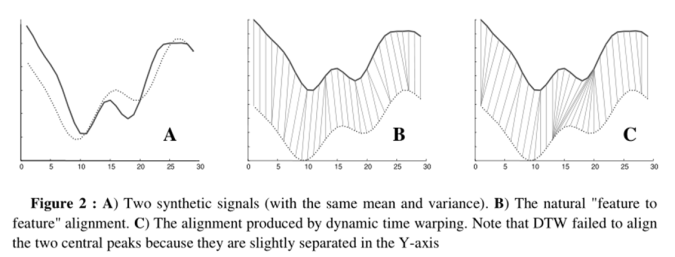

已经提出了很多临时的方法来缓解这种奇点问题，这些方法都具有一个共同点，即基本上都限制了可能的“扭曲”。但是，它们造成的缺点是，可能阻止发现“正确的”“扭曲”。 因此，我们引入了Derivative DTW 来改进这种问题。

4、导数动态时间规整算法

如前文所述，DTW算法粗暴地（wildly）根据Y轴变量的值对X轴进行warp，这样在Y轴变量有细微变动时很容易造成奇点问题，如下图所示。而最正确的时间序列的对齐应该是特征之间的对应（feature to feature），于是我们考虑比DTW更高一层次的特征选取，根据形状（shape）来进行对齐。 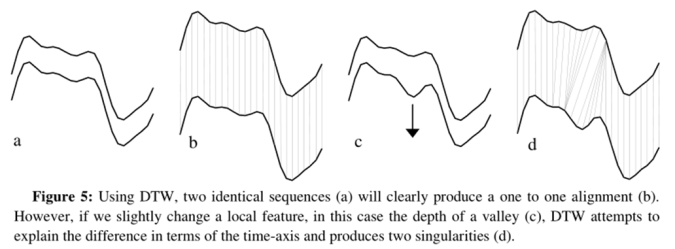image.png

4.1、DDTW算法细节

那么如何才能获取关于形状的信息，我们知道一阶导数可以反映斜率，而斜率是我们判断时间序列形状的一个指数，因此我们通过考虑序列的一阶导数来获得有关形状的信息，因此将我们的算法称为Derivative Dynamic Time Warping(DDTW)。 如前所述，我们构造了一个n×m矩阵，其中矩阵的（i th，j th）元素包含两个点q i和c j之间的距离d（q i，c j）。DTW算法根据欧式距离来计算两个时间序列对应点之间的距离，DDTW则通过qi和cj之间估计导数差值的平方来代替DTW算法的距离公式。在这里我们不去考虑繁琐精确的一阶导数计算公式，反之我们使用简单的导数估计方法，以增加方法的泛化性。估计导数公式如下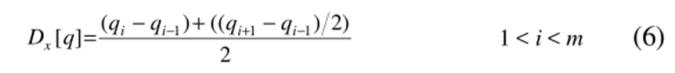： image.png 大家可以看到，该估计值只是通过该点及其左邻点的直线的斜率以及通过左邻点和右邻点的直线的斜率的平均值来得出的。值得注意的是该公式比仅利用两个数据点对于离群点更具有鲁棒性。另外值得注意的是该公式并不包括第一个与最后一个点，反之是运用第二个点与倒数第二个点来代替。 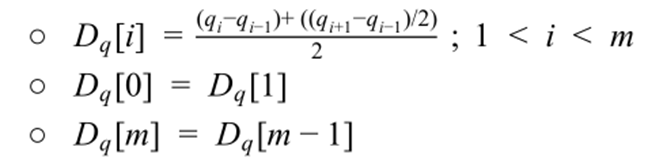image.png 以下是简单的一个例子。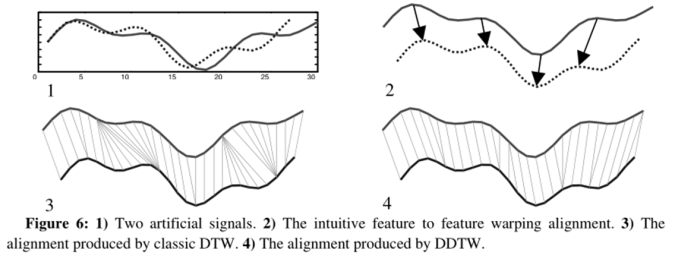 image.png

5、实验与结果

为了验证DDTW对于奇点问题的改进，作者设计了两个实验分别从正反两个方面来进行论证。

5.1 错误的规整（spurious warping）

为了简便地对比两种算法的差异，我们采用较为简单的K值（规整路径的长度）来进行计算。其中K的取值范围在max(m,n)<K<m+n-1。同时由于在该实验中两条时间序列的长度相似，因此m ≤ K < 2m-1。于是我们定义W为warp的次数，因此我们得到以下公式： image.png

W可以反映两种算法warp扭曲的次数，如果算法在两个序列之间没有发现扭曲，则W将等于零；扭曲越多，发现W的值越大。对于上文所述三个数据集，我们进行多次实验并取平均值后得到以下结果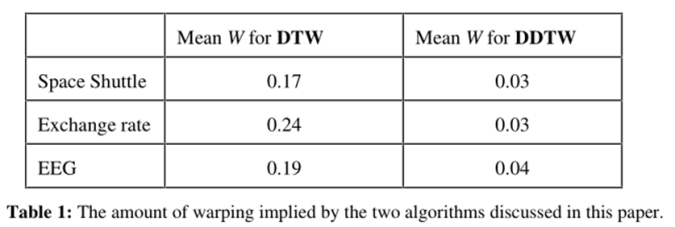： image.png

通过实验，DTW尝试粗暴（wild）的通过时间轴的扭曲来纠正序列之间的微小差异。相应的DDTW则因为考虑“更高层次的特征”从而更不容易发现不存在的warp。 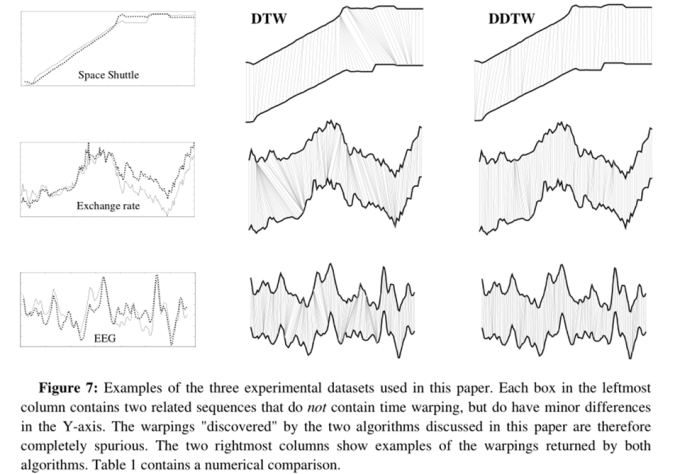image.png 在这里值得注意的是，由于这三组时间序列是高度相关但不相同的，并且在Y轴上包含细微的差别，所以对于这三组时间序列分别的warp其实是完全错误的（completely spurious）。也就是说两种算法找到的warp越多，那么他们对于奇点问题的识别排出就越差。因此我们可以看到，DDTW在奇点问题上对于DTW具有很大的提升。

5.2 寻找正确的“扭曲”（find the correct warping）

该实验是为了验证两种算法对于需要warp的时间序列的敏感性。因此作者通过一条时间序列Q与时间序列Q的复制Q''来进行实验。简单来说，作者通过对时间序列Q''插入三种不同水平的Gaussian bump以达到对时间序列在Y轴上的细微变化，再通过两种算法对时间序列Q和Q''进行warp，观察算法的效果。 与第一个实验相同，我们设定M为错误warp的次数，并且在以下条件下得到公式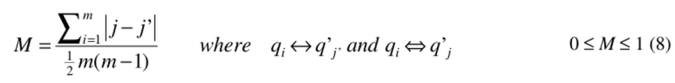： image.png

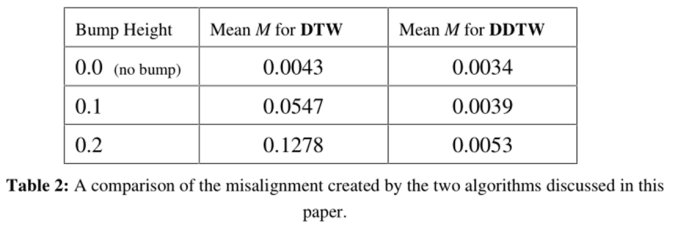
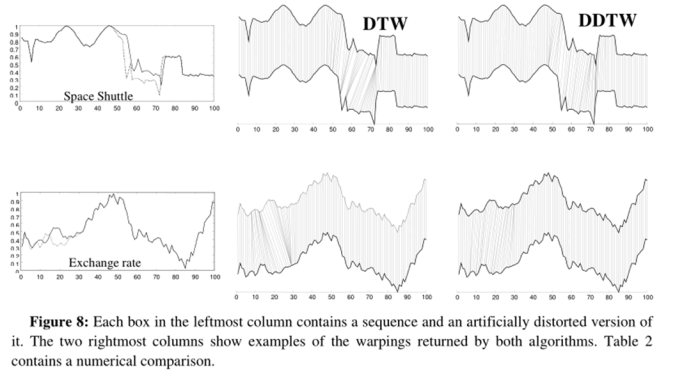
条件中的双箭头对应表示时间序列Q与Q''之间正确的对应关系，单箭头对应表示由算法返回的实际对应关系。当且仅当两个条件都符合时，我们计算两条时间序列对应Y轴变量的差值。公示中分母是为了标准化而做的计算。 分析公式8我们可以知道，当时间序列上对应点正确匹配时，差值为零，如果算法产生了很多奇点，那么M的值就会越大，因此我们可以通过该公式比较两种算法对于寻找正确warp的能力。实验结果如下： image.png

由以上实验可知，DDTW可在时间序列之间产生出色的对齐方式；并且DDTW可以更好地找到两个序列之间的正确变形。

6、参考资料

论文：Eamonn J. Keogh, Derivative Dynamic Time Warping 暂无论文实验数据，仅提供参考代码，供大家学习理解：https://momodel.cn/explore/5d837ba0870b9dc68fd13fdc?type=app

关于我们

Mo（网址：https://momodel.cn）是一个支持 Python 的人工智能在线建模平台，能帮助你快速开发、训练并部署模型。

Mo 人工智能俱乐部 是由网站的研发与产品设计团队发起、致力于降低人工智能开发与使用门槛的俱乐部。团队具备大数据处理分析、可视化与数据建模经验，已承担多领域智能项目，具备从底层到前端的全线设计开发能力。主要研究方向为大数据管理分析与人工智能技术，并以此来促进数据驱动的科学研究。

目前俱乐部每两周在杭州举办线下论文分享与学术交流。希望能汇聚来自各行各业对人工智能感兴趣的朋友，不断交流共同成长，推动人工智能民化、应用普及化。 image.png

DTW动态时间规整算法

DTW动态时间规整算法

[TOC]

1、基本介绍

  • DTW：Dynamic Time Warping，即动态时间归整。DTW算法基于DP动态规划思想，解决了发音长短不一的模板匹配问题，常用于语音识别（孤立词识别）。

  • HMM算法在训练阶段需要提供大量的语音数据，通过反复急速那才能得到模型参数；而DTW算法的训练中几乎不需要额外的计算。因此DTW算法得到了广泛使用。

2、算法原理（理论原理）

无论在训练和建立模板阶段还是在识别阶段，都先采用端点算法确定语音的起点和终点。

2.1 主要术语

  • 参考模板：以存入模板库的各个词条成为参考模板，可以理解为训练集，表示形式为：

    $$R = {R(1), R(2), ..., R(m), ..., R(M)}$$

其中，m为训练语音帧的时序标号，m=1为起点语音帧，m=M为终点语音帧，因此M为该模板所包含的语音帧总数，R(m)为第m帧的语音特征矢量。

  • 测试模板：需要识别的一个输入词条语音，可以理解为测试集，表示形式为：

    $$T = {T(1), T(2), ..., T(n), ..., T(N)}$$

其中，n为测试语音帧的时序标号，n=1为起点语音帧，n=N为终点语音帧，因此N为该模板所包含的语音帧总数，T(n)为第n帧的语音特征矢量。

  • 重点：参考模板与测试模板一半采用相同类型的特征矢量（MFCC、FPC系数）、相同的帧长、相同的窗函数和相同的帧移。

2.2 算法由来和改进过程

  • 传统方法：

    • 首先，需要比较相似度，一般采用欧式距离$D[T, R]$，距离越小则相似度越高。为了计算失真距离，应该让T和R中各个对应帧之间的距离算起。

    • 若N=M，则可以直接计算$d(T,R) = \sqrt{(T_{1} - R_{1})^{2} + (T_{2} - R_{2})^{2} + ...+ (T_{N} - R_{N})^{2}}$

    • 若N<M，则需要将T(n)和R(m)对对齐。对齐采用线性扩张的方法，即将测试模板T线性映射为一个M帧（参考模板长度）的序列，再计算测试模板T与参考模板R的欧式距离。

  • 改进方法（采用DP算法）：由于传统方法计算没有考虑到语音各个段在不同情况下的持续时间会产生或短或长的变化，因此识别效果不佳。更多的是采用动态规划DP算法。

    • 具体实施方法：可以将测试模板和参考模板投影到一个二维直角坐标系中，测试模板的各个帧号可以在横轴上标出，参考模板的各个帧号可以在纵轴上标出。通过这些表示帧号的证书坐标画出一些纵横线即可形成一个网络，网络中的每一个交叉点(n,m)表示测试模式中某一帧的交汇点。

    • 其中的DP算法：DP算法可以归结为寻找一条通过此网络中若干格点的路径，路径通过的格点即为测试和参考模板中进行计算的帧号。

    • 描述路劲：假设路径通过的所有格点依次为：(n1, m1), ..., (ni, mi), ..., (nN, mM)，其中(n1,m1)=(1,1)，(nN, mM)=(N,M)。路径函数为Oslash，如果路径已经通过格点(n,m)，那么下一个通过的格点(n,m)只可能是下列三种情况在之一：

      • (n,m) -> (n+1, m+1)

      • (n,m) -> (n+1, m+1)

      • (n,m) -> (n, m+1) 用$\eta$描述上述三个约束条件，则求最佳路径的问题可以归结为满足约束条件时 ，求最佳路劲函数m=&Oslash。使得沿着路劲的积累距离达到最小值。

      • 最佳路径函数Oslash？？？

    • 搜索该路径的方法为：搜索从(n,m)点出发，可以展开若干条满足$\eta$的路径，假设可计算每条路径达到(n,m)点时的积累距离，具有最小积累距离者即为最佳路径。容易证明，由于约束条件$\eta$，点(n,m)一定选择(n-1,m-1)、(n-1,m)和(n,m-1)等这3个距离之路径延伸通过，此卢晶晶的积累距离为： $$D[(n,m)] = d[T(n), R(m)] + \min{D(n-1,m-1), D(n-1, m), D(n,m-1)}$$ 因此从(n,m)=(1,1)出发搜索(n,m)，对每一个(n,m)都存储相应的距离，这个距离是当前格点的匹配距离与前一个累计距离最小的格点。搜索到(n,m)时，只保留一条最佳路径。通过逐点向前寻找就可以求得整条路劲，这套DP算法便是DTW算法。

    • 总结：DTW算法可以直接按照描述来实现，即分配两个NxM的矩阵，分别为积累距离矩阵D和帧匹配距离矩阵d，其中帧匹配距离矩阵d(i,j)的值为测试模板的第i帧与参考模板的第j帧间的距离。D(N,M)即为最佳匹配路径所对应的匹配距离。

2.3 DTW算法流程

  • 等待完善

  • 代码实现

3、算法DTW和算法HMM的比较

  • 优点：

    • （1）DTW算法本身简单且有效，而HMM算法比较复杂，对于孤立词识别，在相同条件下，两者算法的识别效果相差不大。

    • （2）HMM需要在训练阶段提供大量的语音数据，通过反复计算才能得到参数模型，而DTW算法的训练中几乎不需要额外的计算。

  • 缺点：

    • （1）DTW算法没有一个有效地用统计方法进行训练的框架，不容易将底层和顶层的各种知识用到语音识别模型中，因此在解决大词汇量、连续语音、非特定语音识别问题时较之HMM相形见绌。而HMM是一种用参数表示的，用于描述随机过程统计特性的概率模型。

参考：

  1. DTW算法：https://baike.baidu.com/item/dtw/3219286?fr=aladdin

  2. DTW原理实现：https://blog.csdn.net/ljh0302/article/details/50884303

python – django中的动态数据库表

python – django中的动态数据库表

我正在开发一个项目,该项目要求我使用该用户的用户名创建一个在网站上注册的每个用户的表.表中的列对于每个用户都是相同的.

在研究时我发现了这个Django dynamic model fields.我不知道如何使用django-mutant来实现这个目标.另外,有没有办法在不使用任何外部应用程序的情况下执行此操作？

PS：我使用的后端是MysqL

最佳答案
一个有趣的问题,可能会引起更广泛的兴趣.

为每个用户创建一个表是维护的噩梦.您应该定义一个表来保存所有用户的数据,然后使用数据库的功能仅检索与感兴趣的用户相关的那些行(如果需要,在检查权限之后,因为给任何用户不受限制不是一个好主意访问其他用户的数据,但未设置特定权限).

采用您提出的解决方案需要您构造包含相关用户的表名的sql语句.对数据库的连续查询通常会有所不同,这会减慢工作量,因为每个sql语句都必须“准备好”(必须检查语法,必须验证表和列的名称,请求用户的权限)必须授权访问命名资源,等等.

通过使用单个表(模型),可以重复使用相同的查询,其中参数用于改变特定数据值(在这种情况下是正在搜索其数据的用户的名称).您的数据库工作将更快地进行,您只需要一个模型来描述所有用户的数据,并且数据库管理不会是一场噩梦.

另一个优点是Django(您似乎正在使用)具有广泛的基于用户的权限模型,并且可以轻松地用于验证用户登录(一旦您知道如何).这些优点非常引人注目,我希望你能从你的异端中退出,并决定你可以使用单个表(并且,如果你计划使用标准的Django登录,那么与用户模型的关系,作为任何Django的核心部分)项目).

在您继续操作时,请随时提出更多问题.您似乎对数据库工作不熟悉,因此我尝试提供适当级别的详细信息.如果您无法访问知识渊博的建议,则存在许多此类陷阱. SO上的人会帮助你.

python+tkinter制作一个可自定义的动态时钟及详细解释，珍藏版

python+tkinter制作一个可自定义的动态时钟及详细解释，珍藏版

1.效果图

2.完整代码

#第1步：导出模块
from tkinter import *
import math,time
#第2步：定义窗口的相关设置
root = Tk()
root.title("a DIY clock") #定义窗口名称
root.geometry("1020x800+500+0") #位置坐标=500,0=就是顶格向右水平移动500
root.configure(bg=''pink'') #定义窗口的背景颜色
#第3步：定义全局变量
global List #定义全局变量，list列表
global i   #定义i
List = [] #定义了一个初始化空的list


#第4步：定义一个画布canvas,大小、背景颜色
canvas = Canvas(root,width=400, height=500,bg=''green'')
canvas.pack() #居中顶上线pack的特点
#生成外圆，圆内填充颜色是fill设置
canvas.create_oval(50, 50, 350, 350,fill=''orange'') 
#生成外圆，可以引申复习一下：canvas的画图形学习，画圆、长方形、正方形、椭圆形

#附加：如果在root的tk窗口上还有其他的东西，建议放在这里设置
#如果放在while循环后面，因为一旦进入while循环时，就不能停止，除非停止才进行下一步，才显示。
#而显示动态的时间是一个死循环，故建议放在while循环前进行设置
#设置字体最大20，与label的属性有关
label=Label(root,text=''新年快乐'',width=10,height=1,font=20,fg=''red'')
label.pack() #label位置的方法一
#label.place(x=400,y=501) #canvas的height=500，还是pack好，窗口大小改变，依旧居中顶在画画布下

#第5步：定义时针上的刻度1~12h
def points():
    for i in range(1,13): #定义时针刻度（1~12h）
        x = 200 + 130*math.sin(2*math.pi*i/12)
        y = 200 - 130*math.cos(2*math.pi*i/12)
        #时针上的小时刻度的显示，位置，字体大小,注意字体颜色是用fill，不是color或者fg或bg
        canvas.create_text(x,y,text=i,font=10,fill=''red'') 
points() #生成数字

#第6步：定义指针=时针、分针、秒针
def createline(radius,line_width,rad):
    x = 200 + radius * math.sin(rad)
    y = 200 - radius * math.cos(rad)
    #指针的设置，包括时针、分针、秒针，及颜色fill相当于指针的颜色设置
    i = canvas.create_line(200, 200, x, y, width=line_width,fill=''blue'')
    List.append(i) #列表末尾添加i

#第7步：
#注意时钟是一直循环的，while循环等于1相当于true，一直循环的
#如果不加try和except TclError:pass，那么关闭tk窗口的右上角的’x‘，强制中断，跳出循环，就会报错
try:
#定义循环
    while True:
        tm=time.localtime() #获取当前时间
        #cur_time2 = time.strftime(''%Y-%m-%d %X'', time.localtime())
        #加上文字：当前时间，注意换行符号：\n
        cur_time2 = time.strftime(''当前时间：\n''+''%Y-%m-%d %X'', time.localtime())
        t_hour=0
        if tm.tm_hour<=12:
            t_hour=tm.tm_hour
        else:
            t_hour=tm.tm_hour-12
        #定义指针大小
        rad1=2*math.pi*(t_hour+tm.tm_min/60)/12 #时针
        rad2=2*math.pi*(tm.tm_min+tm.tm_sec/60)/60 #分针
        rad3=2*math.pi*tm.tm_sec/60 #秒针
        #画指针
        createline(50,6,rad1) #时针
        createline(90,3,rad2) #分针
        createline(120,1,rad3) #秒针

        
        #当前时间显示地址、文字显示、字体大小、fill相当于字体颜色设置
        time_text=canvas.create_text(200,450,text=cur_time2,font=10,fill=''purple'')
        root.update() #窗口刷新或更新，因当前时间是一秒一秒跳动的，否则不动了
        time.sleep(1) #暂停1秒，代表秒针是1秒1秒的走动这个循环
        #循环走动一次，及时删除画布上的相关数据，否则有残影
        for j in List:
        #备注这里的i与上面的i不同，是局部变量，也可以设置item或者j
            canvas.delete(j)
        canvas.delete(time_text)
except TclError: #如果出现错误，就是强制跳出死循环，那么pass=忽略跳出
    pass

#循环走起
root.mainloop()
View Code

 

关于Python中的动态时间规整和python动态数据的介绍已经告一段落，感谢您的耐心阅读，如果想了解更多关于DDTW 导数动态时间规整算法、DTW动态时间规整算法、python – django中的动态数据库表、python+tkinter制作一个可自定义的动态时钟及详细解释，珍藏版的相关信息，请在本站寻找。

本文标签：

上一篇交互式Python：尽管line_profiler正确导入，但无法使％lprun正常工作

下一篇使用Python的multiprocessing.Process类（python multiprocessing process）

相关文章