对于想了解PythonDijkstra算法的读者,本文将提供新的信息,我们将详细介绍pythondijkstra算法30个节点运算速度,并且为您提供关于DijkstraAlgorithm迪克特斯拉算法
对于想了解Python Dijkstra算法的读者,本文将提供新的信息,我们将详细介绍python dijkstra算法30个节点运算速度,并且为您提供关于Dijkstra Algorithm 迪克特斯拉算法--Python、Dijkstra算法、Dijkstra算法 (迪杰斯特拉)、Dijkstra算法 c语言实现的有价值信息。
本文目录一览:- Python Dijkstra算法(python dijkstra算法30个节点运算速度)
- Dijkstra Algorithm 迪克特斯拉算法--Python
- Dijkstra算法
- Dijkstra算法 (迪杰斯特拉)
- Dijkstra算法 c语言实现

Python Dijkstra算法(python dijkstra算法30个节点运算速度)
我正在尝试编写Dijkstra的算法,但是我在努力如何在代码中“说”某些事情而苦苦挣扎。为了可视化,这是我要使用数组表示的列:
max_nodes A B C Length Predecessor Visited/UnvisitedA 0 1 2 -1 UB 1 0 1 -1 UC 2 1 0 -1 U因此,将有几个数组,如下面的代码所示:
def dijkstra (graph, start, end)network[max_nodes][max_nodes]state [max_nodes][length]state2 [max_nodes][predecessor]state3 [max_nodes][visited]initialNode = 0 for nodes in graph: D[max_nodes][length] = -1 P[max_nodes][predecessor] = "" V[max_nodes][visited] = false for l in graph: length = lengthFromSource[node] + graph[node][l] if length < lengthFromSourceNode[w]: state[l][length] = x state2[l][predecessor] state3[l][visited] = true x +=1粗体部分是我要坚持的地方-我正在尝试实现算法的这一部分:
3.对于当前节点,请考虑其所有未访问的邻居并计算其暂定距离。
例如,如果当前节点(A)的距离为6,并且将其与另一个节点(B)相连的边为2,则通过A到B的距离将为6 + 2 =
8。如果此距离小于以前记录的距离,则覆盖距离
4。完成考虑当前节点的所有邻居后,将其标记为已访问。访问过的节点将不再被检查;现在记录的距离是最终的和最小的
我认为我走在正确的轨道上,我只是停留在怎么说:“从节点开始,获取从源到节点的长度,如果长度较小,则覆盖先前的值,然后移至下一个节点
答案1
小编典典首先,我认为这是一个作业问题,因为最好的建议是不要自己去写,而是在网络上找到现有的实现。
例如,这看起来不错。
假设您 确实 需要重新设计轮子,那么那里引用的代码将使用字典来存储节点数据。因此,您可以输入以下内容:
{ ''s'': {''u'' : 10, ''x'' : 5}, ''u'': {''v'' : 1, ''x'' : 2}, ''v'': {''y'' : 4}, ''x'': {''u'' : 3, ''v'' : 9, ''y'' : 2}, ''y'': {''s'' : 7, ''v'' : 6}}这似乎是呈现图形信息的更直观的方法。访问的节点和距离也可以保存在字典中。

Dijkstra Algorithm 迪克特斯拉算法--Python
迪克斯拉特算法:
1、找出代价最小的节点,即可在最短时间内到达的节点;
2、更新节点的邻居的开销;
3、重复这个过程,直到图中的每个节点都这样做了;
4、计算最终路径。
''''''
迪克斯特拉算法:
1、以字典的方式更新图,包括权重
2、创建开销字典,关键在于起点临近的点开销为实际数值,其他点为暂时未到达,开销为无穷,随后更新
3、创建父节点列表保存每个点的父节点,以便记录走过的路径
''''''
from queue import LifoQueue
graph = {}
graph[''start''] = {}
graph[''start''][''a''] = 6
graph[''start''][''b''] = 2
graph[''a''] = {}
graph[''a''][''end''] = 4
graph[''b''] = {}
graph[''b''][''a''] = 3
graph[''b''][''c''] = 2
graph[''c''] = {}
graph[''c''][''end''] = 3
graph[''end''] = {}
print(graph)
infinity = float(''inf'')
costs = {}
costs[''a''] = 6
costs[''b''] = 2
costs[''c''] = infinity
costs[''end''] = infinity
parents = {}
parents[''a''] = ''start''
parents[''b''] = ''start''
parents[''c''] = ''b''
parents[''end''] = None
processed = []
def find_lowest_cost_node(costs):
lowest_cost = float(''inf'')
lowest_cost_node = None
for node in costs:
cost = costs[node]
if (cost < lowest_cost and node not in processed):
lowest_cost = cost
lowest_cost_node = node
return lowest_cost_node
node = find_lowest_cost_node(costs)
while(node is not None):
cost = costs[node]
neighbors = graph[node]
for n in neighbors.keys():
new_cost = cost + neighbors[n]
if costs[n] > new_cost:
costs[n] = new_cost
parents[n] = node
processed.append(node)
node = find_lowest_cost_node(costs)
#输出最短路径
p = ''end''
path = LifoQueue()
while(True):
path.put(p)
if(p == ''start''):
break
p = parents[p]
while not path.empty():
print(path.get())

Dijkstra算法
Dijkstra算法:即迪杰斯特拉算法
待续....

Dijkstra算法 (迪杰斯特拉)
定义
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
原理
设图 G=(V,E) 所有顶点的集合为 V,起点为 S,最短路径树中包含的顶点集合为 S。在各计算步骤中,我们将选出最短路径树的边和顶点并将其添加至S。
对于各顶点 i,设仅经由S内的顶点的 s 到 i 的最短路径成本为 d[i], i 在最短路径树中的父节点为 p[i]。
①初始状态下将 S 置空。
初始化 s 的 d[s]=0;除 s 外,所有属于 V 的顶点 i 的 d[i]=∞。
②循环进行下述处理,直至 S=V 为止。
从 V-S 中选出 d[u] 最小的顶点 u。
将 u 添加至 S,同时将与 u 相邻且属于 V-S 的所有顶点 v 的值按照下述方式更新
if(d[u] + w(u,v) < d[v])
d[v] = d[u] + w(u,v) , p[v] = u ;
❗ 显然迪杰斯特拉算法并不能处理负权图。下图中A->B的最短路应为 3=8-5,但用此算法算出来的A->B的最短路为7。
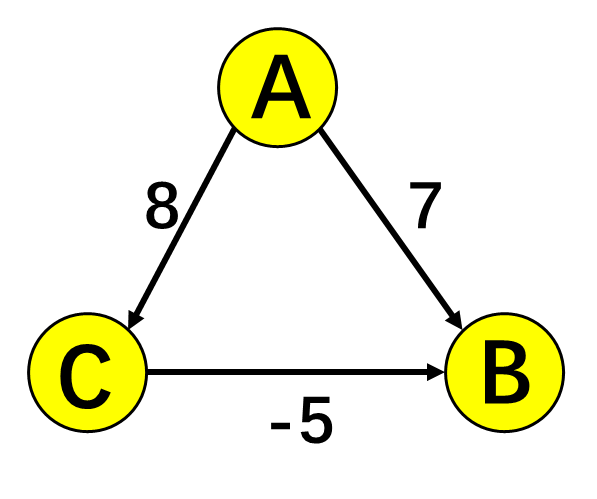
迪杰斯特拉最短路径算法和普利姆算法贼像。:)
实现

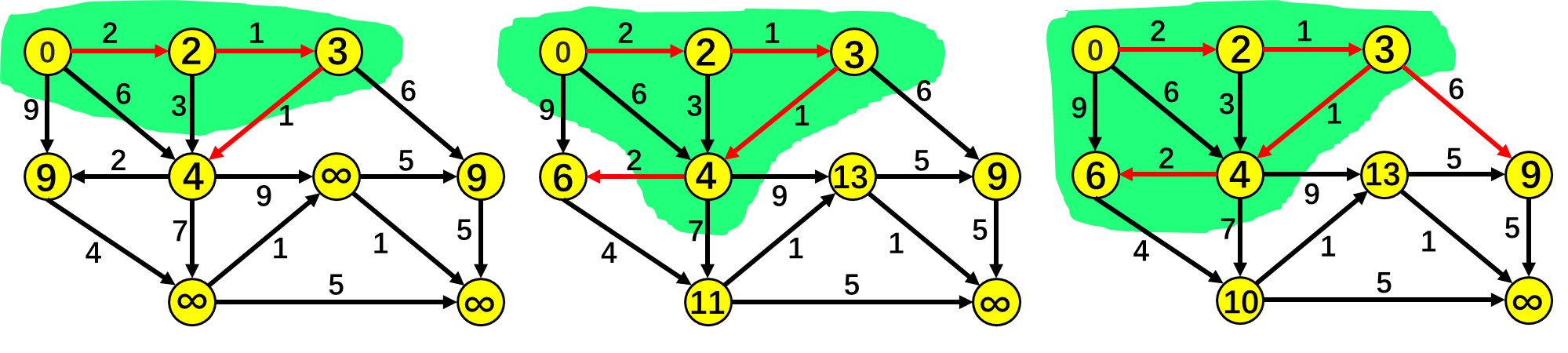
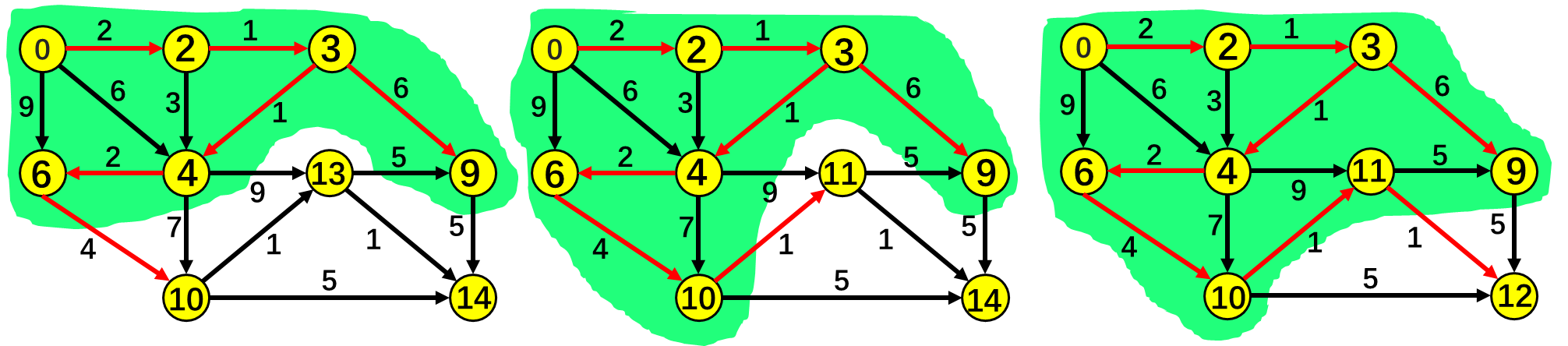
原算法
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int inf=0x3f3f3f3f;
struct node
{
int v,w;
node(){}
node(int a,int b)
{v=a;w=b;}
};
vector<node> e[maxn];
int n,m;
void dij();
int main()
{
int i,u,v,w;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
e[u].push_back(node(v,w));
}
dij();
system("pause");
return 0;
}
void dij()
{
int dis[maxn],vis[maxn]={0},i,j,mmin,f;
fill(dis,dis+maxn,inf);
dis[1]=0;
for(i=1;i<=n;i++)
{
mmin=inf;
for(j=1;j<=n;j++)
if(!vis[j]&&dis[j]<mmin)
mmin=dis[f=j];
vis[f]=1;
for(j=0;j<e[f].size();j++)
{
if(dis[e[f][j].v]>dis[f]+e[f][j].w)
dis[e[f][j].v]=dis[f]+e[f][j].w;
}
}
for(j=1;j<=n;j++)
printf("1->%d %d\n",j,dis[j]);
}优先队列优化
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int inf=0x3f3f3f3f;
struct node
{
int v,w;
node(){}
node(int a,int b)
{v=a;w=b;}
bool operator <(const node &n) const
{return w>n.w;}
};
vector<node> e[maxn];
int n,m;
void dij_queue();
int main()
{
int i,u,v,w;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
e[u].push_back(node(v,w));
}
dij_queue();
system("pause");
return 0;
}
void dij_queue()
{
int dis[maxn],vis[maxn]={0},u,v,w,i;
node p;
priority_queue<node> que;
que.push(node(1,0));
fill(dis,dis+maxn,inf);
dis[1]=0;
while(!que.empty())
{
p=que.top();que.pop();
u=p.v;
if(vis[u]) continue;
vis[u]=1;
for(i=0;i<e[u].size();i++)
{
w=e[u][i].w;v=e[u][i].v;
if(!vis[v]&&dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
que.push(node(v,dis[v]));
}
}
}
for(i=1;i<=n;i++)
printf("1->%d %d\n",i,dis[i]);
}挑战程序设计竞赛(第2版)

Dijkstra算法 c语言实现
Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。 Dijkstra算法 能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
例如,对下图中的有向图,应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。

Dijkstra算法的迭代过程:
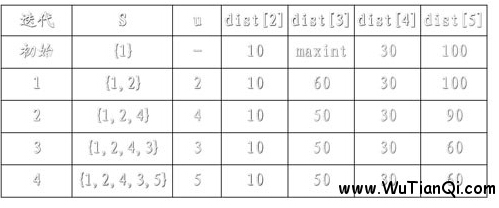
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#define X 10000
#define VertexNum 7 //实际上共有六个顶点(1---6)
#define EdgeNum 9
int Graph[VertexNum][VertexNum] =
//0 1 2 3 4 5 6
{ X, X, X, X, X, X, X, //0
X, X, 6, 3, X, X, X, //1
X, X, X, X, 5, X, X, //2
X, X, 2, X, 3, 4, X, //3
X, X, X, X, X, X, 3, //4
X, X, X, X, 2, X, 5, //5
X, X, X, X, X, X, X //6
};
int Visited[VertexNum];
int path[VertexNum];
int Distance[VertexNum];
void Dijkstra(int Begin)
{
int MinEdge, Vertex, i,j, Edges;
Edges = 1;
Visited[Begin] = 1;
for (i = 1; i<VertexNum; i++) Distance[i] = Graph[Begin][i];
Distance[Begin] = 0;
printf(" 1 2 3 4 5 6\\n");
printf("-----------------------------------\\n");
printf("s:%d", Edges);
for( i=1; i<VertexNum; i++)
if (Distance[i] == X) printf(" *"); else printf("%3d",Distance[i]);
printf("\\n");
while( Edges<VertexNum-1)
{
Edges++; MinEdge = X;
for(j=1; j<VertexNum; j++)
if (Visited[j]==0 && MinEdge > Distance[j] )
{
Vertex = j; MinEdge = Distance[j];
}
Visited[Vertex] = 1;
printf("s:%d",Edges);
for(j=1; j<VertexNum; j++)
{
if (Visited[j] == 0 && Distance[Vertex] + Graph[Vertex][j] <Distance[j])
{ Distance[j] = Distance[Vertex] + Graph[Vertex][j];
path[j] = Vertex;
}
//printf("%6d",Distance[j]);
if (Distance[j] == X) printf(" *"); else printf("%3d",Distance[j]);
}
printf("\\n");
}
}
void main()
{
int i;
int k;
// clrscr();
for(i=0; i<VertexNum; i++) { Visited[i] = 0; path[i] = 1;}
Dijkstra(1);
printf("\\n\\nAll Path-------------------------\\n");
for(i=2; i<VertexNum; i++) //printf("%5d",Visited[i]);
{
printf("[%d] ",Distance[i]);
k = i;
do
{
printf("%d<--",k);
k = path[k];
} while (k!=1);
printf("1 \\n");
}
}
以上代码参考了数据结构课本
下面的是网上的代码:
以下是具体的实现(C/C++):
/***************************************
* About: 有向图的Dijkstra算法实现
* Author: Tanky Woo
* Blog: www.WuTianQi.com
***************************************/
#include <iostream>
using namespace std;
const int maxnum = 100;
const int maxint = 999999;
void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])
{
bool s[maxnum]; // 判断是否已存入该点到S集合中
for(int i=1; i<=n; ++i)
{
dist[i] = c[v][i];
s[i] = 0; // 初始都未用过该点
if(dist[i] == maxint)
prev[i] = 0;
else
prev[i] = v;
}
dist[v] = 0;
s[v] = 1;
// 依次将未放入S集合的结点中,取dist[]最小值的结点,放入结合S中
// 一旦S包含了所有V中顶点,dist就记录了从源点到所有其他顶点之间的最短路径长度
for(int i=2; i<=n; ++i)
{
int tmp = maxint;
int u = v;
// 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!s[j]) && dist[j]<tmp)
{
u = j; // u保存当前邻接点中距离最小的点的号码
tmp = dist[j];
}
s[u] = 1; // 表示u点已存入S集合中
// 更新dist
for(int j=1; j<=n; ++j)
if((!s[j]) && c[u][j]<maxint)
{
int newdist = dist[u] + c[u][j];
if(newdist < dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
}
void searchPath(int *prev,int v, int u)
{
int que[maxnum];
int tot = 1;
que[tot] = u;
tot++;
int tmp = prev[u];
while(tmp != v)
{
que[tot] = tmp;
tot++;
tmp = prev[tmp];
}
que[tot] = v;
for(int i=tot; i>=1; --i)
if(i != 1)
cout << que[i] << " -> ";
else
cout << que[i] << endl;
}
int main()
{
freopen("input.txt", "r", stdin);
// 各数组都从下标1开始
int dist[maxnum]; // 表示当前点到源点的最短路径长度
int prev[maxnum]; // 记录当前点的前一个结点
int c[maxnum][maxnum]; // 记录图的两点间路径长度
int n, line; // 图的结点数和路径数
// 输入结点数
cin >> n;
// 输入路径数
cin >> line;
int p, q, len; // 输入p, q两点及其路径长度
// 初始化c[][]为maxint
for(int i=1; i<=n; ++i)
for(int j=1; j<=n; ++j)
c[i][j] = maxint;
for(int i=1; i<=line; ++i)
{
cin >> p >> q >> len;
if(len < c[p][q]) // 有重边
{
c[p][q] = len; // p指向q
c[q][p] = len; // q指向p,这样表示无向图
}
}
for(int i=1; i<=n; ++i)
dist[i] = maxint;
for(int i=1; i<=n; ++i)
{
for(int j=1; j<=n; ++j)
printf("%8d", c[i][j]);
printf("\n");
}
Dijkstra(n, 1, dist, prev, c);
// 最短路径长度
cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl;
// 路径
cout << "源点到最后一个顶点的路径为: ";
searchPath(prev, 1, n);
}
输入数据:
5
7
1 2 10
1 4 30
1 5 100
2 3 50
3 5 10
4 3 20
4 5 60
输出数据:
999999 10 999999 30 100
10 999999 50 999999 999999
999999 50 999999 20 10
30 999999 20 999999 60
100 999999 10 60 999999
源点到最后一个顶点的最短路径长度: 60
源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5
最后给出两道题目练手,都是直接套用模版就OK的:
1.HDOJ 1874 畅通工程续
http://www.wutianqi.com/?p=1894
2.HDOJ 2544 最短路
http://www.wutianqi.com/?p=1892
本文同步分享在 博客“shiter”(CSDN)。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。
今天关于Python Dijkstra算法和python dijkstra算法30个节点运算速度的讲解已经结束,谢谢您的阅读,如果想了解更多关于Dijkstra Algorithm 迪克特斯拉算法--Python、Dijkstra算法、Dijkstra算法 (迪杰斯特拉)、Dijkstra算法 c语言实现的相关知识,请在本站搜索。
本文标签:





