对于如何简化sympy中指数的对数？感兴趣的读者，本文将会是一篇不错的选择，我们将详细介绍指数运算python，并为您提供关于5.2Python数据处理篇之Sympy系列(二)---Sympy的基本操

对于如何简化sympy中指数的对数？感兴趣的读者，本文将会是一篇不错的选择，我们将详细介绍指数运算python，并为您提供关于5.2Python数据处理篇之Sympy系列(二)---Sympy的基本操作、5.3Python 数据处理篇之 Sympy 系列 (三)--- 简化操作、C++ 函数的未来展望：新特性将如何简化代码开发？、NumPy：以n为底的对数的有用信息。

本文目录一览：

• 如何简化sympy中指数的对数？（指数运算python）
• 5.2Python数据处理篇之Sympy系列(二)---Sympy的基本操作
• 5.3Python 数据处理篇之 Sympy 系列 (三)--- 简化操作
• C++ 函数的未来展望：新特性将如何简化代码开发？
• NumPy：以n为底的对数

如何简化sympy中指数的对数？（指数运算python）

当我打字

import sympy as spx = sp.Symbol(''x'')sp.simplify(sp.log(sp.exp(x)))

我得到

log(e^x)

代替x。我知道此功能“没有保证”。

题。 是否有一些特定的简化（通过级数展开或其他方式）将指数的对数转换为恒等函数？

答案1

小编典典

您必须设置x为实型，您的代码才能工作：

import sympy as spx = sp.Symbol(''x'', real=True)print(sp.simplify(sp.log(sp.exp(x))))

输出：x。

对于x该公式的复杂结果，并不总是等于x。例子在这里。

5.2Python数据处理篇之Sympy系列(二)---Sympy的基本操作

目录

[TOC]

前言

符号化运算也是数值运算中的一个主要的领域，今天我们来学习以下，python里强大的符号运算库---sympy。今天讲的是第一讲，sympy的操作。

对应于官网的：Basic Operations

Basic Operation s：

https://docs.sympy.org/latest/tutorial/basic_operations.html

（一）符号的初始化与输出设置-symbol() symbols() latex()

1.作用：

在sympy里进行符号运算之前，必须先定义sympy的符号，这样sympy才能识别该符号。

.init_printing(use_latex=True)开启时，在jupyter运行时，输出的是LaTeX的格式

使用：latex()函数，同样返回LaTeX的格式。

2.操作：

（1）说明：

符号的初始化分为两种形式：

1. 单个符号的初始化：x = sympy.Symbol(''x'')
2. 多个符号的初始化：x,y=sympy.symbol("x y")

（2）源代码：

import sympy as sy

# 符号化变量
x = sy.Symbol(''x'')
y, z = sy.symbols(''y z'')

# 输出设置
sy.init_printing(use_latex=True)

# 输出结果
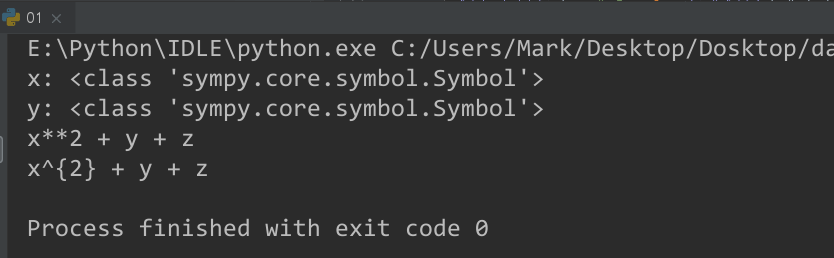
print("x:", type(x))
print("y:", type(y))
print(x**2+y+z)
print(sy.latex(x**2+y+z))

（3）输出效果

（二）替换符号-subs(old,new)

1.说明：

sub是Substitution的简称，也就是替换，其有两个作用：

语法是：expr.sub(old,new)

1. 数值替换，用数值替换符号，进行带入计算。
2. 符号替换，用一些符号替换符号。

2.源代码：

from sympy import *

# 符号化变量
x, y, z = symbols(''x y z'')

expr = x**2+1

# 数值替换
result = expr.subs(x, 2)
print("原式：", expr)
print("数值计算的结果：", result)

# 符号替换
new_expr = expr.subs(x, y+z)
print("符号替换的结果：", new_expr)

3.输出效果:

4.注意点：

（1）是否改变原表达式

subs()函数不改变原表达式，并且返回一个修改的表达式。

（2）替换多个表达式

当需要替换多个表达式时，可以在subs()里使用列表

如：subs([(x,2), (y, 3), (z, 4)])

表示：将x替换成2，y替换成3，z替换成4

（三）将字符串变为sympy的表达式-sympify（）

1.说明：

不要混淆了sympify()函数与 simplify()函数，前者是转化，后者是简化。

2.源代码：

from sympy import *

string = "x**2+2*y + z/2"

# 转化
expr = sympify(string)

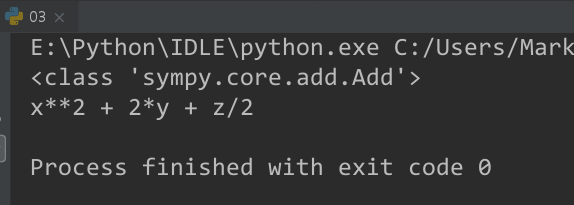
print("类型：", type(expr))
print("表达式：", expr)

3.输出效果：

（四）数值计算-evalf()

1.说明：

相当于python自带的eval()函数，只是进行的是float浮点数运算。

2.操作：

（1）对于数值表达式的运算

直接使用.evalf()函数

from sympy import *

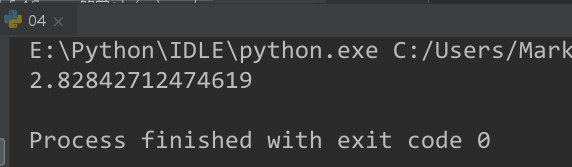
expr = sqrt(8)

# 进行计算
result = expr.evalf()

print(result)

（2）对于符号表达式的运算

对于表达式常用的是:

.evalf(subs={x: 2.4})

from sympy import *

# 符号化
x = Symbol(''x'')

# 进行计算
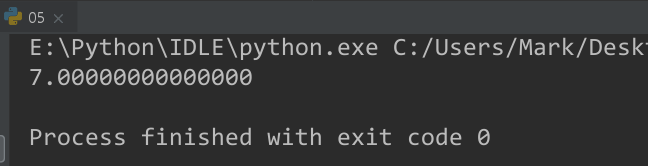
expr = x**2+3
result = expr.evalf(subs={x: 2})

print(result)

（五）自定义表达式-lambdify（）

1.说明：

该函数有点类似于lambda（）,用于自己构造一个函数表达

2.源代码：

from sympy import *
import numpy as np

x = Symbol(''x'')

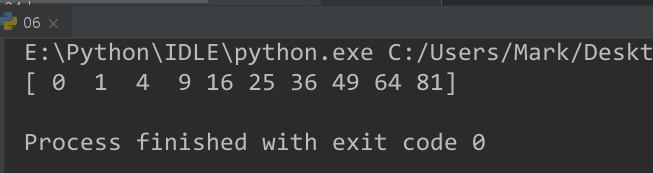
a = np.arange(10)

expr = x**2

# 构造自己的函数
f = lambdify(x, expr, "numpy")

print(f(a))

3.输出效果：

作者：Mark

日期：2019/03/15 周五

5.3Python 数据处理篇之 Sympy 系列 (三)--- 简化操作

5.3 简化操作

目录

[TOC]

前言

既然 sympy 是对于符号的运算，那么它对于符号表达式的简化与展开一定很强大。

今天我们学习的是符号表达式的简化与展开。

本章节对应官网的 Simplification

官网的 Simplification

https://docs.sympy.org/latest/tutorial/simplification.html

（一）有理数与多项式的简化

1. 最简化 - simplify（）

（1）说明：

simplify（）是尽可能的让表达式最简化，其最简化的形式是不定的。

####　（2）源代码：

from sympy import *


x = Symbol(''x'')

expr1 = cos(x)**2+sin(x)**2

expr2 = (x**3 + x**2 - x - 1)/(x**2 + 2*x + 1)

# 简化表达式
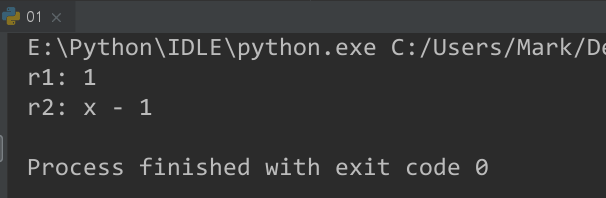
r1 = simplify(expr1)
r2 = simplify(expr2)

print(r1)
print(r2)

（3）输出：

$cos(x)^2+sin(x)^2$-->1

$(x^3 + x^2 - x - 1)/(x^2 + 2x + 1)$-->$x-1$

2. 展开 - expand（）

（1）说明：

expand（）是对括号里的多项式进行展开。

（2）源代码：

from sympy import *

x = Symbol(''x'')

expr1 = (x+1)**2
expr2 = ((x + 1)*(x - 2) - (x - 1)*x)

# 展开
r1 = expand(expr1)
r2 = expand(expr2)

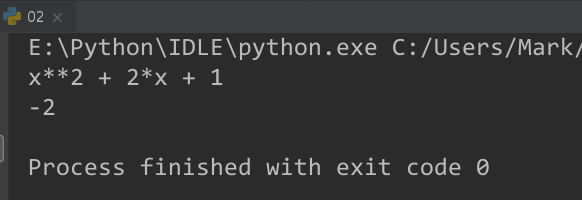
print(r1)
print(r2)

（3）输出：

$(x+1)^2$-->$x^2+2x+1$

$(x + 1)(x - 2) - (x - 1)x$-->-2

3. 提公因式 - factor（）

（1）说明：

factor（）是对展开的多项式进行提公因式

（2）源代码：

from sympy import *

x = Symbol(''x'')

expr1 = (x ** 3 - x ** 2 + x - 1)

# 提公因数
r1 = factor(expr1)

print(r1)
print(latex(expr1))
print(latex(r1))

（3）输出：

$x^{3} - x^{2} + x - 1$-->$\left(x - 1\right) \left(x^{2} + 1\right)$

4. 合并同类项 - ceiling（）

（1）说明：

对于多项式进行合并同类项

（2）源代码：

from sympy import *

x = Symbol(''x'')
y = Symbol(''y'')
z = Symbol(''z'')

expr1 = x*y + x - 3 + 2*x**2 - z*x**2 + x**3
expr2 = x**3+x*2-3*x**2+x**3-x**2+x*4-5

# 合并同类项
r1 = ceiling(expr1)
r2 = ceiling(expr2)

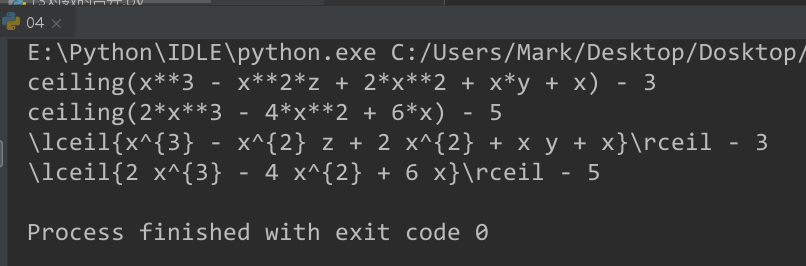
print(r1)
print(r2)
print(latex(r1))
print(latex(r2))

（3）输出：

$xy + x - 3 + 2x^2 - zx^2 + x^3$ --> $\lceil{x^{3} - x^{2} z + 2 x^{2} + x y + x}\rceil - 3$

$x^3+x2-3x^2+x^3-x^2+x4-5$ --> $\lceil{2 x^{3} - 4 x^{2} + 6 x}\rceil - 5$

5. 简化分式 - cancel（）

（1）说明：

cancle 既有约分又有简化的作用

（2）源代码：

from sympy import *

x = Symbol(''x'')

expr1 = (x**2 + 2*x + 1)/(x**2 + x)
expr2 = 1/x + (3*x/2 - 2)/(x - 4)

# 约分消去分式的公因数
r1 = cancel(expr1)

# 简化分式
r2 = cancel(expr2)

# 结果
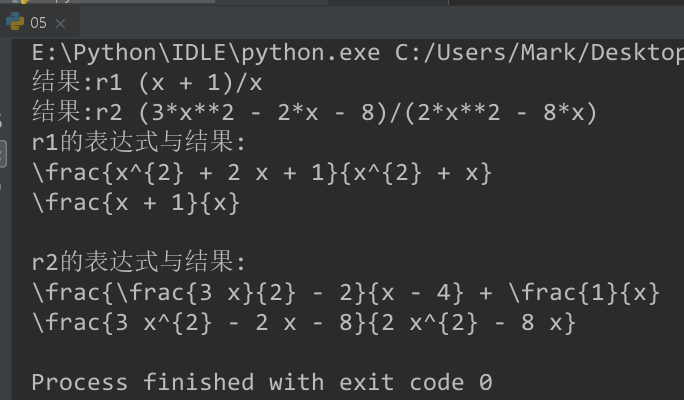
print("结果:r1", r1)
print("结果:r2", r2)

# r1的表达式与结果
print("r1的表达式与结果:")
print(latex((x**2 + 2*x + 1)/(x**2 + x)))
print(latex(r1))


# r2的表达式与结果
print("\nr2的表达式与结果:")
print(latex(1/x + (3*x/2 - 2)/(x - 4)))
print(latex(r2))

（3）输出：

$\frac{x^{2} + 2 x + 1}{x^{2} + x}$ --》 $\frac{x + 1}{x}$

$\frac{\frac{3 x}{2} - 2}{x - 4} + \frac{1}{x}$ --》 $\frac{3 x^{2} - 2 x - 8}{2 x^{2} - 8 x}$

6. 分式展开 - apart（）

（1）说明：

原本只有一项的分式表达式，展开为多项的分式表达式。

（2）源代码：

from sympy import *

x = Symbol(''x'')

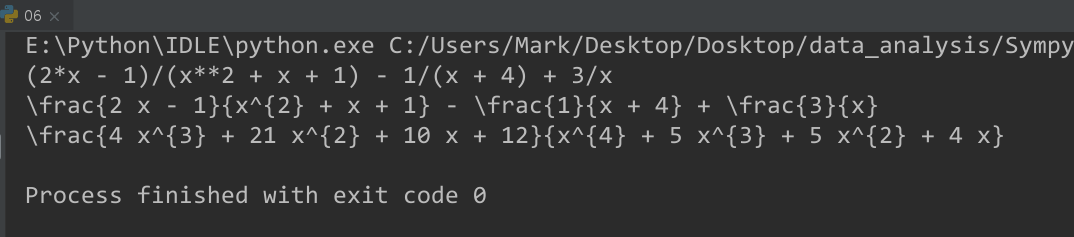
expr1 = (4*x**3 + 21*x**2 + 10*x + 12)/(x**4 + 5*x**3 + 5*x**2 + 4*x)

# 对于分式进行展开
r1 = apart(expr1)

print(r1)
print(latex(r1))
print(latex(expr1))

（3）输出：

4x3+21x2+10x+12x4+5x3+5x2+4x

---》 2x−1x2+x+1−1x+4+3x

（二）三角函数的简化

1. 三角形的简化 - trigsimp（）

####　（１）说明：

使用 trigsimp（）可以简化三角函数，反三角函数也可以。

####　（２）源代码：

from sympy import *

x = Symbol(''x'')

expr1 = sin(x)**2+cos(x)**2
expr2 = sin(x)**4 - 2*cos(x)**2*sin(x)**2 + cos(x)**4

# 进行三角形简化
r1 = trigsimp(expr1)
r2 = trigsimp(expr2)


print("r1:", r1)
print("r2:", r2)

# r1的latex
print("="*20)
print("expr1-latex:", latex(expr1))
print("r1-latex:", latex(r1))

# r2的latex
print("="*20)
print("expr2-latex:", latex(expr2))
print("r2-latex:", latex(r2))

####　（３）输出：

$\sin^{2}{\left (x \right )} + \cos^{2}{\left (x \right )}$ --> $1$

$\sin^{4}{\left (x \right )} - 2 \sin^{2}{\left (x \right )} \cos^{2}{\left (x \right )} + \cos^{4}{\left (x \right )}$ --> $\frac{\cos{\left (4 x \right )}}{2} + \frac{1}{2}$

2. 三角形的展开 - expand_trig ()

（１）说明：

使用 expand_trig () 可以展开三角函数，同样反三角函数也可以。

（２）源代码：

from sympy import *

x = Symbol(''x'')
y = Symbol(''y'')

expr1 = sin(x+y)
expr2 = tan(2*x)

# 三角形的展开
r1 = expand_trig(expr1)
r2 = expand_trig(expr2)

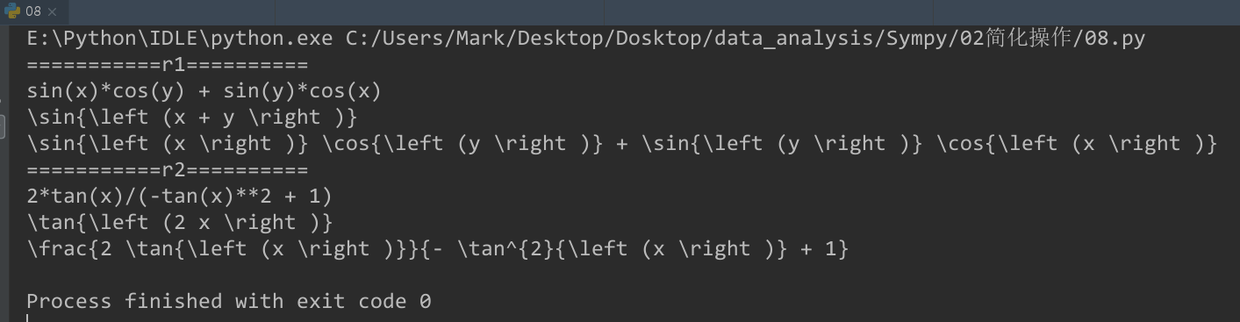
print("===========r1==========")
print(r1)
print(latex(expr1))
print(latex(r1))

print("===========r2==========")
print(r2)
print(latex(expr2))
print(latex(r2))

（３）输出：

$\sin{\left (x + y \right )}$ --> $\sin{\left (x \right )} \cos{\left (y \right )} + \sin{\left (y \right )} \cos{\left (x \right )}$

$\tan{\left (2 x \right )}$ --> $\frac{2 \tan{\left (x \right )}}{- \tan^{2}{\left (x \right )} + 1}$

（三）指数函数的简化

1. 指数的合并一 - powsimp ()

（１）说明：

powsimp () 主要用于同底数或者同指数

（２）源代码：

from sympy import *

# 假设 x与y 是正值， a 是真实的值
x = Symbol(''x'', positive=True)
y = Symbol(''y'', positive=True)
a = Symbol(''a'', real=True)

expr1 = x**2*x**3
expr2 = x**a*y**a


# 进行指数的合并，如果不符合，则不进行简化
r1 = powsimp(expr1)
r2 = powsimp(expr2)


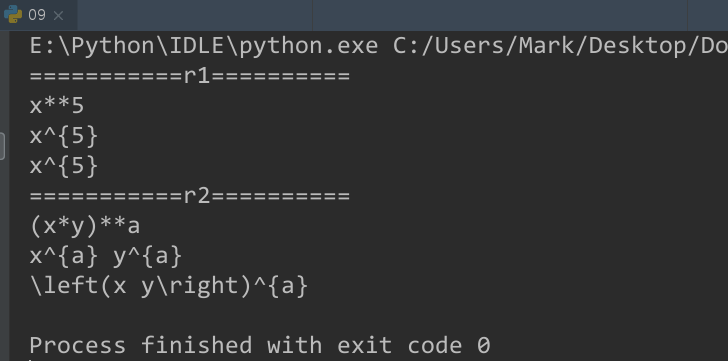
print("===========r1==========")
print(r1)
print(latex(expr1))
print(latex(r1))

print("===========r2==========")
print(r2)
print(latex(expr2))
print(latex(r2))

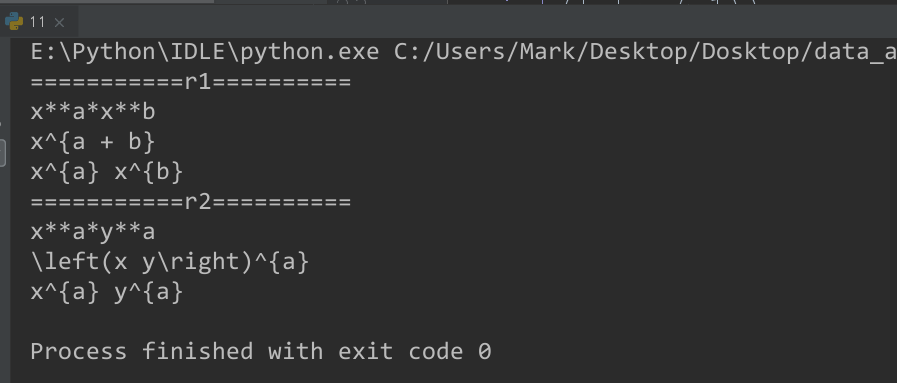
（３）输出：

$x^2x^3$ --> $x^5$

$x^ay^b$ --> $\left(x y\right)^{a}$

2. 指数的合并二 - powdenest ()

（１）说明：

powdenest () 主要用于只有一个底数的不同指数。

（２）源代码：

from sympy import *

# 假设 x与y 是正值， a 是真实的值
x = Symbol(''x'', positive=True)
y = Symbol(''y'', positive=True)
a = Symbol(''a'', real=True)
b = Symbol(''b'', real=True)

expr1 = (x**a)**b
expr2 = (((x**2)**a)**b)


# 进行指数的合并，如果不符合，则不进行简化
r1 = powdenest(expr1)
r2 = powdenest(expr2)


print("===========r1==========")
print(r1)
print(latex(expr1))
print(latex(r1))

print("===========r2==========")
print(r2)
print(latex(expr2))
print(latex(r2))

（３）输出：

$(x^a)^b$ --> $x^{ab}$

${{x^2}^a}^b$ --> $x^{2ab}$

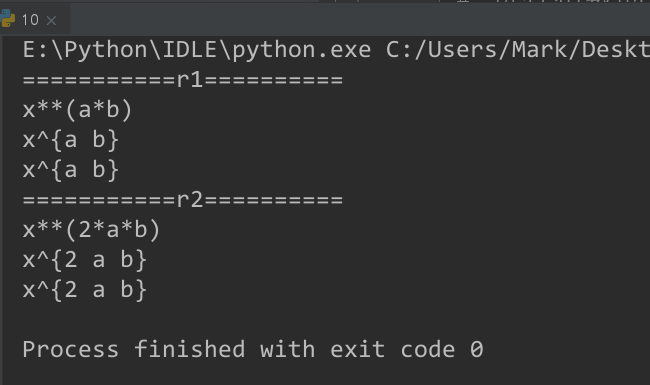
3. 指数的展开：-expand_power_exp\expand_power_base

（１）说明：

1. expand_power_exp () 用于同底数的展开
2. expand_power_base () 用于同指数的展开

（２）源代码：

from sympy import *

# 假设 x与y 是正值， a 是真实的值
x = Symbol(''x'', positive=True)
y = Symbol(''y'', positive=True)
a = Symbol(''a'', real=True)
b = Symbol(''b'', real=True)

expr1 = x**(a+b)
expr2 = (x*y)**a


# 进行指数的展开
# 底数相同展开
r1 = expand_power_exp(expr1)

# 指数相同展开
r2 = expand_power_base(expr2)


print("===========r1==========")
print(r1)
print(latex(expr1))
print(latex(r1))

print("===========r2==========")
print(r2)
print(latex(expr2))
print(latex(r2))

（３）输出：

$x^{a+b}$ --> $x^{a} x^{b}$

$\left(x y\right)^{a}$ --> $x^{a} y^{a}$

（四）对数函数的简化

1. 对数的简化 - logcombine ()

（１）说明：

logcombine () 用于合并对数。

（２）源代码：

from sympy import *

# 假设 x与y 是正值， a 是真实的值
x = Symbol(''x'', positive=True)
y = Symbol(''y'', positive=True)
n = Symbol(''n'', real=True)

expr1 = log(x) + log(y)
expr2 = log(x) - log(y)
expr3 = n*log(x)


# 对于对数的展开
r1 = logcombine(expr1)
r2 = logcombine(expr2)
r3 = logcombine(expr3)

print(r1)
print(r2)
print(r3)

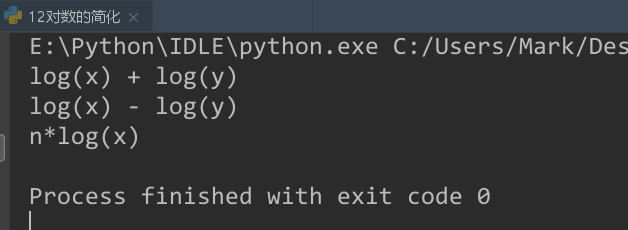
（３）输出：

$log(x) + log(y)$ --> $log(xy)$

$log(x)-log(y)$ --> $\log(xy)$

$n\log(x)$ --> $log(x^n)$

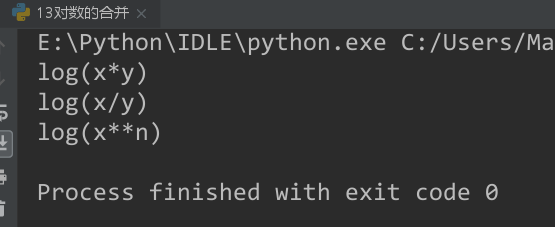
2. 对数的展开 - expand_log（）

（１）说明：

expand_log（）用于对数的展开。

（２）源代码：

from sympy import *

# 假设 x与y 是正值， a 是真实的值
x = Symbol(''x'', positive=True)
y = Symbol(''y'', positive=True)
n = Symbol(''n'', real=True)

expr1 = log(x*y)
expr2 = log(x/y)
expr3 = log(x**n)


# 对于对数的展开
r1 = expand_log(expr1)
r2 = expand_log(expr2)
r3 = expand_log(expr3)

print(r1)
print(r2)
print(r3)

（３）输出：

$log(xy)$ --> $log(x)+log(y)$

$log(x/y)$ --> $log(x)-\log(y)​$

$log(x^n)$ --> ​$n\log(x)$

（五）其他函数的简化

###　１. 阶乘与排列组合 - factorial ()\binomial ()

（１）说明：

1. factorial () 用于求阶乘
2. binomial () 用于求排列组合

（２）源代码：

from sympy import *

n = Symbol("n")

# 求阶乘
r1 = factorial(3)
r2 = factorial(n)


print(r1)
print(r2)

# 排列组合
print(binomial(4, 2))

（３）输出：

作者：Mark

日期：2019/03/16 周六

C++ 函数的未来展望：新特性将如何简化代码开发？

c++++ 函数特性将革新代码开发，其新特性包括：范围约束：确保传入函数的参数类型满足指定约束。constexpr 函数：在编译期间执行函数，加快程序运行速度。声明折叠：消除冗余声明，使代码简洁。

C++ 函数的未来展望：新特性如何简化代码开发？

随着 C++ 语言的不断发展，其函数特性也迎来了重大创新。这些特性旨在简化代码开发，提高程序员的工作效率。本文将探讨未来 C++ 函数即将推出的新特性，并深入研究它们的实际应用。

新特性概览

C++ 即将推出的函数新特性包括：

• 范围约束 (concepts)：确保传入函数的参数类型符合指定约束。
• constexpr 函数：允许在编译期间执行函数，从而加快程序运行速度。
• 声明折叠：消除冗余的声明，使代码更加简洁。

实战案例

范围约束

考虑以下排序函数：

立即学习“C++免费学习笔记（深入）”；

使用范围约束，我们可以指定 arr 参数必须是一个可遍历数据类型，并且 size 参数必须是一个无符号整型：

这确保了我们只能为排序函数传入有效的参数，并有助于防止类型错误。

constexpr 函数

考虑以下获取文件大小的函数：

使用 constexpr 函数，我们可以将此函数的计算移到编译期：

这显著提高了程序运行速度，因为在运行时无需实际调用该函数。

声明折叠

考虑以下声明两组相似类型的函数：

使用声明折叠，我们可以将这组声明合并为：

这极大地减少了代码冗余，使代码更易于维护。

结论

C++ 函数即将推出的新特性将通过简化代码开发、提高程序性能以及增强代码简洁性，为程序员提供强大的优势。这些特性为 C++ 的未来提供了令人振奋的前景，值得密切关注其发展趋势。

以上就是C++ 函数的未来展望：新特性将如何简化代码开发？的详细内容，更多请关注php中文网其它相关文章！

NumPy：以n为底的对数

从有关对数的numpy文档中，我发现了以
e
，2和10为底取对数的函数：

import numpy as npnp.log(np.e**3) #3.0np.log2(2**3)   #3.0np.log10(10**3) #3.0

但是，如何在numpy中使用以 n 为底的对数（例如42）？

答案1

小编典典

要使用自定义底数获取对数，请使用math.log：

import mathnumber = 74088  # = 42**3base = 42exponent = math.log(number, base)  # = 3

要使用自定义底数获取对数，请使用numpy.log：

import numpy as nparray = np.array([74088, 3111696])  # = [42**3, 42**4]base = 42exponent = np.log(array) / np.log(base)  # = [3, 4]

如您所料，请注意默认情况下np.log(np.e) == 1.0。

---

提醒一下，对数基数更改规则是：

今天的关于如何简化sympy中指数的对数？和指数运算python的分享已经结束，谢谢您的关注，如果想了解更多关于5.2Python数据处理篇之Sympy系列(二)---Sympy的基本操作、5.3Python 数据处理篇之 Sympy 系列 (三)--- 简化操作、C++ 函数的未来展望：新特性将如何简化代码开发？、NumPy：以n为底的对数的相关知识，请在本站进行查询。

本文标签：

• Python
• SymPy
• 指数运算
• 对数简化