本文将带您了解关于CodeforcesRound#435(Div.2)-异或规律&思维-MahmoudandEhabandthexor的新内容，同时我们还将为您解释异或的代码的相关知识，另外，我们还将
本文将带您了解关于Codeforces Round #435 (Div. 2)-异或规律&思维-Mahmoud and Ehab and the xor的新内容，同时我们还将为您解释异或的代码的相关知识，另外，我们还将为您提供关于CF 959 E. Mahmoud and Ehab and the xor-MST、CF959E Mahmoud and Ehab and the xor-MST 思维、Codeforces #396 (Div. 2) D. Mahmoud and a Dictionary （并查集+map、Codeforces 1099 B. Squares and Segments-思维(Codeforces Round #530 (Div. 2))的实用信息。
本文目录一览：- Codeforces Round #435 (Div. 2)-异或规律&思维-Mahmoud and Ehab and the xor（异或的代码）
- CF 959 E. Mahmoud and Ehab and the xor-MST
- CF959E Mahmoud and Ehab and the xor-MST 思维
- Codeforces #396 (Div. 2) D. Mahmoud and a Dictionary （并查集+map
- Codeforces 1099 B. Squares and Segments-思维(Codeforces Round #530 (Div. 2))
Codeforces Round #435 (Div. 2)-异或规律&思维-Mahmoud and Ehab and the xor（异或的代码）
总结
以上是小编为你收集整理的Codeforces Round #435 (Div. 2)-异或规律&思维-Mahmoud and Ehab and the xor全部内容。
如果觉得小编网站内容还不错，欢迎将小编网站推荐给好友。
CF 959 E. Mahmoud and Ehab and the xor-MST
E. Mahmoud and Ehab and the xor-MST
https://codeforces.com/contest/959/problem/E
分析：
每个点x应该和x ^ lowbit(x)连边，那么现在就是求$\sum_{i=1}^{n}lowbit(i)$，然后打表找规律。
代码：
1 #include<cstdio>
2 #include<algorithm>
3 #include<cstring>
4 #include<iostream>
5 #include<cmath>
6 #include<cctype>
7 #include<set>
8 #include<queue>
9 #include<vector>
10 #include<map>
11 using namespace std;
12 typedef long long LL;
13
14 inline int read() {
15 int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch==''-'')f=-1;
16 for(;isdigit(ch);ch=getchar())x=x*10+ch-''0'';return x*f;
17 }
18
19 int main() {
20 LL n, res = 0;
21 cin >> n; n--;
22 for (LL x = 1; x <= n; x <<= 1)
23 res += ((n - x) / (x + x) + 1) * x;
24 cout << res;
25 return 0;
26 }
CF959E Mahmoud and Ehab and the xor-MST 思维
Ehab is interested in the bitwise-xor operation and the special graphs. Mahmoud gave him a problem that combines both. He has a complete graph consisting of n vertices numbered from 0 to n - 1. For all 0 ≤ u < v < n, vertex u and vertex v are connected with an undirected edge that has weight 
(where 
is the bitwise-xor operation). Can you find the weight of the minimum spanning tree of that graph?
You can read about complete graphs in https://en.wikipedia.org/wiki/Complete_graph
You can read about the minimum spanning tree in https://en.wikipedia.org/wiki/Minimum_spanning_tree
The weight of the minimum spanning tree is the sum of the weights on the edges included in it.
The only line contains an integer n (2 ≤ n ≤ 1012), the number of vertices in the graph.
The only line contains an integer x, the weight of the graph''s minimum spanning tree.
44In the first sample: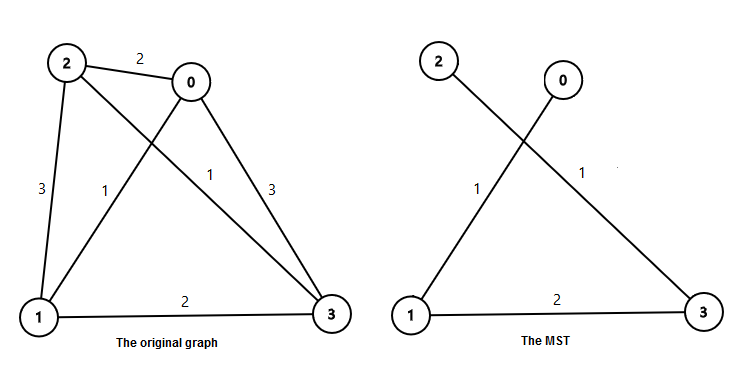 
The weight of the minimum spanning tree is 1+2+1=4.
题意翻译
n个点的完全图标号(0-n-1),i和j连边权值为i^j,求MST的值
不妨先手算几项，可以发现每一位上的贡献为当前n 的一半；
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 300005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
inline ll rd() {
ll x = 0;
char c = getchar();
bool f = false;
while (!isdigit(c)) {
if (c == ''-'') f = true;
c = getchar();
}
while (isdigit(c)) {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }
/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) {
x = 1; y = 0; return a;
}
ans = exgcd(b, a%b, x, y);
ll t = x; x = y; y = t - a / b * y;
return ans;
}
*/
ll qpow(ll a, ll b, ll c) {
ll ans = 1;
a = a % c;
while (b) {
if (b % 2)ans = ans * a%c;
b /= 2; a = a * a%c;
}
return ans;
}
int main()
{
//ios::sync_with_stdio(0);
ll n; rdllt(n);
ll ans = 0;
ll tmp = 1;
while (n>1) {
ans += tmp * (n >> 1); tmp <<= 1; n -= (n >> 1);
// cout << n<<'' ''<<ans << endl;
}
cout << ans << endl;
return 0;
}
Codeforces #396 (Div. 2) D. Mahmoud and a Dictionary （并查集+map
总结
以上是小编为你收集整理的Codeforces #396 (Div. 2) D. Mahmoud and a Dictionary （并查集+map全部内容。
如果觉得小编网站内容还不错，欢迎将小编网站推荐给好友。
Codeforces 1099 B. Squares and Segments-思维(Codeforces Round #530 (Div. 2))
B. Squares and Segments
Little Sofia is in fourth grade. Today in the geometry lesson she learned about segments and squares. On the way home, she decided to draw nn squares in the snow with a side length of 11. For simplicity, we assume that Sofia lives on a plane and can draw only segments of length 11, parallel to the coordinate axes, with vertices at integer points.
In order to draw a segment, Sofia proceeds as follows. If she wants to draw a vertical segment with the coordinates of the ends (x,y)(x,y) and (x,y+1)(x,y+1). Then Sofia looks if there is already a drawn segment with the coordinates of the ends (x′,y)(x′,y) and (x′,y+1)(x′,y+1) for some x′x′. If such a segment exists, then Sofia quickly draws a new segment, using the old one as a guideline. If there is no such segment, then Sofia has to take a ruler and measure a new segment for a long time. Same thing happens when Sofia wants to draw a horizontal segment, but only now she checks for the existence of a segment with the same coordinates xx, x+1x+1 and the differing coordinate yy.
For example, if Sofia needs to draw one square, she will have to draw two segments using a ruler:
After that, she can draw the remaining two segments, using the first two as a guide:
If Sofia needs to draw two squares, she will have to draw three segments using a ruler:
After that, she can draw the remaining four segments, using the first three as a guide:
Sofia is in a hurry, so she wants to minimize the number of segments that she will have to draw with a ruler without a guide. Help her find this minimum number.
The only line of input contains a single integer nn (1≤n≤1091≤n≤109), the number of squares that Sofia wants to draw.
Print single integer, the minimum number of segments that Sofia will have to draw with a ruler without a guide in order to draw nn squares in the manner described above.
122344
题意就是找最接近当前数的一个数的两个因数，比如41，就是6*7，就是6+7的结果。如果按照41来算，那么需要41+1=42，如果是按照42来算，就是6+7，还有10，最接近的是3+4，是12的，就是这样的题目。
代码:
1 //B
2 #include<iostream>
3 #include<cstdio>
4 #include<cstring>
5 #include<algorithm>
6 #include<bitset>
7 #include<cassert>
8 #include<cctype>
9 #include<cmath>
10 #include<cstdlib>
11 #include<ctime>
12 #include<deque>
13 #include<iomanip>
14 #include<list>
15 #include<map>
16 #include<queue>
17 #include<set>
18 #include<stack>
19 #include<vector>
20 using namespace std;
21 typedef long long ll;
22
23 const double PI=acos(-1.0);
24 const double eps=1e-6;
25 const ll mod=1e9+7;
26 const int inf=0x3f3f3f3f;
27 const int maxn=2e7+10;
28 const int maxm=100+10;
29 #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
30
31 int main()
32 {
33 int n;
34 cin>>n;
35 int p=sqrt(n);
36 int ans=inf,flag=0;
37 if(n==1){
38 ans=2;
39 cout<<ans<<endl;
40 return 0;
41 }
42 if(p*p==n)ans=min(2*p,ans);
43 else if(p*(p+1)>=n) ans=min(p+p+1,ans);
44 else ans=min(2*(p+1),ans);
45 cout<<ans<<endl;
46 }
我们今天的关于Codeforces Round #435 (Div. 2)-异或规律&思维-Mahmoud and Ehab and the xor和异或的代码的分享就到这里，谢谢您的阅读，如果想了解更多关于CF 959 E. Mahmoud and Ehab and the xor-MST、CF959E Mahmoud and Ehab and the xor-MST 思维、Codeforces #396 (Div. 2) D. Mahmoud and a Dictionary （并查集+map、Codeforces 1099 B. Squares and Segments-思维(Codeforces Round #530 (Div. 2))的相关信息，可以在本站进行搜索。
本文标签：
