对于想了解DepthMapPredictionfromaSingleImageusingaMulti-ScaleDeepNetwork的读者，本文将提供新的信息，并且为您提供关于AlexNet:Ima

对于想了解Depth Map Prediction from a Single Image using a Multi-Scale Deep Network的读者，本文将提供新的信息，并且为您提供关于AlexNet: ImageNet Classification with Deep Convolutional Neural Networks、AlexNet论文翻译-ImageNet Classification with Deep Convolutional Neural Networks、Communication-Efficient Learning of Deep Networks from Decentralized Data、COMPRESSING DEEP CONVOLUTIONAL NETWORKS USING VECTOR QUANTIZATION 论文笔记的有价值信息。

本文目录一览：

• Depth Map Prediction from a Single Image using a Multi-Scale Deep Network
• AlexNet: ImageNet Classification with Deep Convolutional Neural Networks
• AlexNet论文翻译-ImageNet Classification with Deep Convolutional Neural Networks
• Communication-Efficient Learning of Deep Networks from Decentralized Data
• COMPRESSING DEEP CONVOLUTIONAL NETWORKS USING VECTOR QUANTIZATION 论文笔记

Depth Map Prediction from a Single Image using a Multi-Scale Deep Network

AlexNet: ImageNet Classification with Deep Convolutional Neural Networks

[TOC]

AlexNet

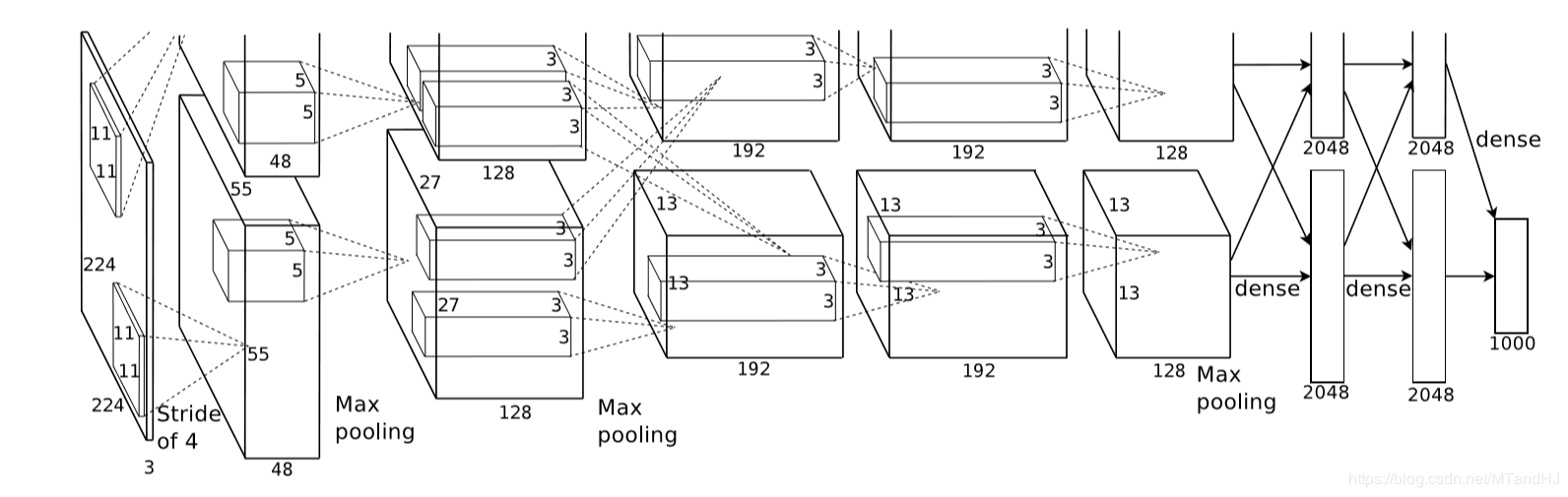
上图是论文的网络的结构图，包括5个卷积层和3个全连接层，作者还特别强调，depth的重要性，少一层结果就会变差，所以这种超参数的调节可真是不简单.

激活函数

首先讨论的是激活函数，作者选择的不是$f(x)=\mathrm{tanh}(x)=(1+e^{-x})^{-1}$，而是ReLUs ( Rectified Linear Units)——$f(x)=\max (0, x)$, 当然，作者考虑的问题是比赛的那个数据集，其网络的收敛速度为: 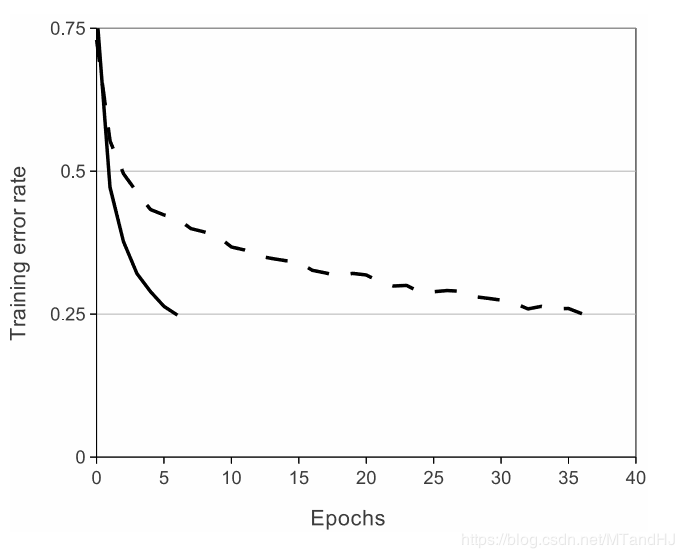接下来，作者讨论了标准化的问题，说ReLUs是不需要进行这一步的，论文中的那句话我感觉理解的怪怪的:

ReLUs have the desirable property that they do not require input normalization to prevent them fromsaturating.

饱和？

然后是关于池化层的部分，一般的池化层的核是不用重叠的，作者这部分也考虑进去了.

防止过拟合

为了防止过拟合，作者提出了他的几点经验.

增加数据

这个数据不是简单的多找点数据，而是通过一些变换使得数据增加.

比如对图片进行旋转，以及PCA提主成分，改变score等.

Dropout

多个模型，进行综合评价是防止过拟合的好方法，但是训练网络不易，dropout, 即让隐层的神经元以一定的概率输出为0来，所以每一次训练，网络的结构实际上都是不一样的，但是整个网络是共享参数的，所以可以一次性训练多个模型?

细节

batch size： 128 momentum: 0.9 weight decay: 0.0005

一般的随机梯度下降好像是没有weight decay这一部分的，但是作者说，实验中这个的选择还是蛮有效的.

代码

"""
epochs: 50
lr: 0.001
batch_size = 128
在训练集上的正确率达到了97%, 
在测试集上的正确率为83%.
"""
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
import os






class AlexNet(nn.Module):

    def __init__(self, output_size=10):
        super(AlexNet, self).__init__()
        self.conv1 = nn.Sequential(  # 3 x 227 x 227
            nn.Conv2d(3, 96, 11, 4, 0),  # 3通道 输出96通道 卷积核为11 x 11 滑动为4 不补零
            nn.BatchNorm2d(96),
            nn.ReLU()
        )
        self.conv2 = nn.Sequential(  # 96 x 55 x 55
            nn.Conv2d(48, 128, 5, 1, 2),
            nn.BatchNorm2d(128),
            nn.ReLU(),
            nn.MaxPool2d(3, 2)
        )
        self.conv3 = nn.Sequential(  # 256 x 27 x 27
            nn.Conv2d(256, 192, 3, 1, 1),
            nn.BatchNorm2d(192),
            nn.ReLU(),
            nn.MaxPool2d(3, 2)
        )
        self.conv4 = nn.Sequential(  # 384 x 13 x 13
            nn.Conv2d(192, 192, 3, 1, 1),
            nn.BatchNorm2d(192),
            nn.ReLU()
        )
        self.conv5 = nn.Sequential(  # 384 x 13 x 13
            nn.Conv2d(192, 128, 3, 1, 1),
            nn.BatchNorm2d(128),
            nn.ReLU(),
            nn.MaxPool2d(3, 2)
        )
        self.dense = nn.Sequential(
            nn.Linear(9216, 4096),
            nn.BatchNorm1d(4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, 4096),
            nn.BatchNorm1d(4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, output_size)
        )

    def forward(self, input):
        x = self.conv1(input)
        x1, x2 = x[:, :48, :, :], x[:, 48:, :, :]  # 拆分
        x1 = self.conv2(x1)
        x2 = self.conv2(x2)
        x = torch.cat((x1, x2), 1)  # 合并
        x1 = self.conv3(x)
        x2 = self.conv3(x)
        x1 = self.conv4(x1)
        x2 = self.conv4(x2)
        x1 = self.conv5(x1)
        x2 = self.conv5(x2)
        x = torch.cat((x1, x2), 1)
        x = x.view(-1, 9216)
        output = self.dense(x)
        return output


class Train:

    def __init__(self, lr=0.001, momentum=0.9, weight_decay=0.0005):
        self.net = AlexNet()
        self.criterion = nn.CrossEntropyLoss()
        self.opti = torch.optim.SGD(self.net.parameters(),
                                    lr=lr, momentum=momentum,
                                    weight_decay=weight_decay)
        self.generate_path()


    def gpu(self):
        self.device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
        if torch.cuda.device_count() > 1:
            print("Let''us use %d GPUs" % torch.cuda.device_count())
            self.net = nn.DataParallel(self.net)
        self.net = self.net.to(self.device)



    def generate_path(self):
        """
        生成保存数据的路径
        :return:
        """
        try:
            os.makedirs(''./paras'')
            os.makedirs(''./logs'')
            os.makedirs(''./images'')
        except FileExistsError as e:
            pass
        name = self.net.__class__.__name__
        paras = os.listdir(''./paras'')
        self.para_path = "./paras/{0}{1}.pt".format(
            name,
            len(paras)
        )
        logs = os.listdir(''./logs'')
        self.log_path = "./logs/{0}{1}.txt".format(
            name,
            len(logs)
        )


    def log(self, strings):
        """
        运行日志
        :param strings:
        :return:
        """
        # a 往后添加内容
        with open(self.log_path, ''a'', encoding=''utf8'') as f:
            f.write(strings)

    def save(self):
        """
        保存网络参数
        :return:
        """
        torch.save(self.net.state_dict(), self.para_path)

    def derease_lr(self, multi=10):
        """
        降低学习率
        :param multi:
        :return:
        """
        self.opti.param_groups()[0][''lr''] /= multi


    def train(self, trainloder, epochs=50):
        data_size = len(trainloder) * trainloder.batch_size
        for epoch in range(epochs):
            running_loss = 0.
            acc_count = 0.
            if (epoch + 1) % 10 is 0:
                self.derease_lr()
                self.log(
                    "learning rate change!!!\n"
                )
            for i, data in enumerate(trainloder):
                imgs, labels = data
                imgs = imgs.to(self.device)
                labels = labels.to(self.device)
                out = self.net(imgs)
                loss = self.criterion(out, labels)
                _, pre = torch.max(out, 1)  #判断是否判断正确
                acc_count += (pre == labels).sum().item() #加总对的个数

                self.opti.zero_grad()
                loss.backward()
                self.opti.step()

                running_loss += loss.data

                if (i+1) % 10 is 0:
                    strings = "epoch {0:<3} part {1:<5} loss: {2:<.7f}\n".format(
                        epoch, i, running_loss * 50
                    )
                    self.log(strings)
                    running_loss = 0.
            self.log(
                "Accuracy of the network on %d train images: %d %%\n" %(
                    data_size, acc_count / data_size * 100
                )
            )
            self.save()

class Test:

    def __init__(self, classes, path=0):
        self.net = AlexNet()
        self.classes = classes
        self.load(path)

    def load(self, path=0):
        if isinstance(path, int):
            name = self.net.__class__.__name__
            path = "./paras/{0}{1}.pt".format(
                name, path
            )
        #加载参数, map_location 因为是用GPU训练的, 保存的是是GPU的模型
        #如果需要在cpu的情况下测试, 选择map_location="cpu".
        self.net.load_state_dict(torch.load(path, map_location="cpu"))
        self.net.eval()

    def showimgs(self, imgs, labels):
        n = imgs.size(0)
        pres = self.__call__(imgs)
        n = max(n, 7)
        fig, axs = plt.subplots(n)
        for i, ax in enumerate(axs):
            img = imgs[i].numpy().transpose((1, 2, 0))
            img = img / 2 + 0.5
            label = self.classes[labels[i]]
            pre = self.classes[pres[i]]
            ax.set_title("{0}|{1}".format(
                label, pre
            ))
            ax.plot(img)
            ax.get_xaxis().set_visible(False)
            ax.get_yaxis().set_visible(False)
        plt.tight_layout()
        plt.show()

    def acc_test(self, testloader):
        data_size = len(testloader) * testloader.batch_size
        acc_count = 0.
        for (imgs, labels) in testloader:
            pre = self.__call__(imgs)
            acc_count += (pre == labels).sum().item()
        return acc_count / data_size

    def __call__(self, imgs):
        out = self.net(imgs)
        _, pre = torch.max(out, 1)
        return pre

AlexNet论文翻译-ImageNet Classification with Deep Convolutional Neural Networks

ImageNet Classification with Deep Convolutional Neural Networks

深度卷积神经网络的ImageNet分类

Abstract

　　We trained a large, deep convolutional neural network to classify the 1.2 million high-resolution images in the ImageNet LSVRC-2010 contest into the 1000 different classes. On the test data, we achieved top-1 and top-5 error rates of 37.5% and 17.0% which is considerably better than the previous state-of-the-art. The neural network, which has 60 million parameters and 650,000 neurons, consists of five convolutional layers, some of which are followed by max-pooling layers, and three fully-connected layers with a final 1000-way softmax. To make training faster, we used non-saturating neurons and a very efficient GPU implementation of the convolution operation. To reduce overfitting in the fully-connected layers we employed a recently-developed regularization method called “dropout” that proved to be very effective. We also entered a variant of this model in the ILSVRC-2012 competition and achieved a winning top-5 test error rate of 15.3%, compared to 26.2% achieved by the second-best entry.

摘要

　　我们训练了一个大型深度卷积神经网络来将ImageNet LSVRC-2010竞赛的120万高分辨率的图像分到1000不同的类别中。在测试数据上，我们得到了top-1 37.5%和top-5 17.0%的错误率，这个结果比目前的最好结果好很多。这个神经网络有6000万参数和650000个神经元，包含5个卷积层（某些卷积层后面带有池化层）和3个全连接层，最后是一个1000维的softmax。为了训练的更快，我们使用了非饱和神经元，并在进行卷积操作时使用了非常有效的GPU。为了减少全连接层的过拟合，我们采用了一个最近开发的名为dropout的正则化方法，结果证明是非常有效的。我们也使用这个模型的一个变种参加了ILSVRC-2012竞赛，赢得了冠军并且与第二名top-5 26.2%的错误率相比，我们取得了top-5 15.3%的错误率。

1 Introduction

　　Current approaches to object recognition make essential use of machine learning methods. To improve their performance, we can collect larger datasets, learn more powerful models, and use better techniques for preventing overfitting. Until recently, datasets of labeled images were relatively small -- on the order of tens of thousands of images (e.g., NORB [16], Caltech-101/256 [8, 9], and CIFAR-10/100 [12]). Simple recognition tasks can be solved quite well with datasets of this size, especially if they are augmented with label-preserving transformations. For example, the current best error rate on the MNIST digit-recognition task (<0.3%) approaches human performance [4]. But objects in realistic settings exhibit considerable variability, so to learn to recognize them it is necessary to use much larger training sets. And indeed, the shortcomings of small image datasets have been widely recognized (e.g., Pinto et al. [21]), but it has only recently become possible to collect labeled datasets with millions of images. The new larger datasets include LabelMe [23], which consists of hundreds of thousands of fully-segmented images, and ImageNet [6], which consists of over 15 million labeled high-resolution images in over 22,000 categories.

1 引言

　　当前的目标识别方法基本上都使用了机器学习方法。为了提高目标识别的性能，我们必须收集更大的数据集，学习更强大的模型，使用更好的技术来防止过拟合。直到最近，标注图像的数据集都相对较小——都在几万张图像的数量级上（例如，NORB[16]，Caltech-101/256 [8, 9]和CIFAR-10/100 [12]）。简单的识别任务在这样大小的数据集上可以被解决的相当好，尤其是如果通过标签保留变换进行数据增强的情况下。例如，目前在MNIST数字识别任务上（<0.3%）的最好准确率已经接近了人类水平[4]。但真实环境中的对象表现出了相当大的可变性，因此为了学习识别它们，有必要使用更大的训练数据集。实际上，小图像数据集的缺点已经被广泛认识到（例如，Pinto et al. [21]），但收集上百万图像的标注数据仅在最近才变得的可能。新的更大的数据集包括LabelMe [23]，它包含了数十万张完全分割的图像，以及包含了22000个类别上的超过1500万张标注的高分辨率的图像ImageNet[6]。

　　To learn about thousands of objects from millions of images, we need a model with a large learning capacity. However, the immense complexity of the object recognition task means that this problem cannot be specified even by a dataset as large as ImageNet, so our model should also have lots of prior knowledge to compensate for all the data we don’t have. Convolutional neural networks (CNNs) constitute one such class of models [16, 11, 13, 18, 15, 22, 26]. Their capacity can be controlled by varying their depth and breadth, and they also make strong and mostly correct assumptions about the nature of images (namely, stationarity of statistics and locality of pixel dependencies). Thus, compared to standard feedforward neural networks with similarly-sized layers, CNNs have much fewer connections and parameters and so they are easier to train, while their theoretically-best performance is likely to be only slightly worse.

　　为了从数百万张图像中学习几千个对象，我们需要一个有很强学习能力的模型。然而对象识别任务的巨大复杂性意味着这个问题不能被特定化，即使通过像ImageNet这样足够大的数据集，因此我们的模型应该也有许多先验知识来补偿我们所没有的数据。卷积神经网络(CNNs)构成了一类这样的模型[16, 11, 13, 18, 15, 22, 26]。它们的容量可以通过改变它们的深度和广度来控制，它们也可以对图像的本质进行强大且通常正确的假设（也就是说，统计的稳定性和像素依赖的局部性）。因此，与具有层次大小相似的标准前馈神经网络相比，CNNs有更少的连接和参数，因此它们更容易训练，而它们理论上的最佳性能可能仅比标准前馈神经网络稍微差一点。

　　Despite the attractive qualities of CNNs, and despite the relative efficiency of their local architecture, they have still been prohibitively expensive to apply in large scale to high-resolution images. Luckily, current GPUs, paired with a highly-optimized implementation of 2D convolution, are powerful enough to facilitate the training of interestingly-large CNNs, and recent datasets such as ImageNet contain enough labeled examples to train such models without severe overfitting.

　　尽管CNN具有引人注目的质量，尽管它们的局部架构相对有效，但是将它们应用到大规模的高分辨率图像中仍然是极其昂贵的。幸运的是，目前的GPU，搭配了高度优化的2D卷积实现，强大到足够促进有趣大量CNN的训练，以及最近的数据集例如ImageNet包含足够多的标注样本来训练这样的模型而没有严重的过拟合。

　　The specific contributions of this paper are as follows: we trained one of the largest convolutional neural networks to date on the subsets of ImageNet used in the ILSVRC-2010 and ILSVRC-2012 competitions [2] and achieved by far the best results ever reported on these datasets. We wrote a highly-optimized GPU implementation of 2D convolution and all the other operations inherent in training convolutional neural networks, which we make available publicly[1]. Our network contains a number of new and unusual features which improve its performance and reduce its training time, which are detailed in Section 3. The size of our network made overfitting a significant problem, even with 1.2 million labeled training examples, so we used several effective techniques for preventing overfitting, which are described in Section 4. Our final network contains five convolutional and three fully-connected layers, and this depth seems to be important: we found that removing any convolutional layer (each of which contains no more than 1% of the model’s parameters) resulted in inferior performance.

　　本文具体的贡献如下：我们在ILSVRC-2010和ILSVRC-2012[2]的ImageNet子集上训练了到目前为止最大的神经网络之一，并取得了迄今为止在这些数据集上报道过的最好结果。我们编写了高度优化的2D卷积GPU实现以及训练卷积神经网络固有的所有其它操作，我们把它公开了¹。我们的网络包含许多新的不寻常的特性，这些特性提高了神经网络的性能并减少了训练时间，详见第三节。即使使用了120万标注的训练样本，我们的网络尺寸仍然使过拟合成为一个明显的问题，因此我们使用了一些有效的技术来防止过拟合，详见第四节。我们最终的网络包含5个卷积层和3个全连接层，深度似乎是非常重要的：我们发现移除任何卷积层（每个卷积层包含的参数不超过模型参数的1%）都会导致更差的性能。

　　In the end, the network’s size is limited mainly by the amount of memory available on current GPUs and by the amount of training time that we are willing to tolerate. Our network takes between five and six days to train on two GTX 580 3GB GPUs. All of our experiments suggest that our results can be improved simply by waiting for faster GPUs and bigger datasets to become available.

最后，网络尺寸主要受限于目前GPU的内存容量和我们能忍受的训练时间。我们的网络在两个GTX 580 3GB GPU上训练五六天。我们的所有实验表明我们的结果可以简单地通过等待更快的GPU和更大的可用数据集来提高。

2 The Dataset

　　ImageNet is a dataset of over 15 million labeled high-resolution images belonging to roughly 22,000 categories. The images were collected from the web and labeled by human labelers using Amazon’s Mechanical Turk crowd-sourcing tool. Starting in 2010, as part of the Pascal Visual Object Challenge, an annual competition called the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC) has been held. ILSVRC uses a subset of ImageNet with roughly 1000 images in each of 1000 categories. In all, there are roughly 1.2 million training images, 50,000 validation images, and 150,000 testing images.

2 数据集

　　ImageNet数据集有超过1500万的标注高分辨率图像，这些图像属于大约22000个类别。这些图像是从网上收集的，使用了亚马逊（Amazon）的Mechanical Turk的众包工具通过人工标注的。从2010年起，作为Pascal视觉对象挑战赛的一部分，每年都会举办ImageNet大规模视觉识别挑战赛（ILSVRC）。ILSVRC使用ImageNet的一个子集，1000个类别每个类别大约1000张图像。总计，大约120万训练图像，50000张验证图像和15万测试图像。

　　ILSVRC-2010 is the only version of ILSVRC for which the test set labels are available, so this is the version on which we performed most of our experiments. Since we also entered our model in the ILSVRC-2012 competition, in Section 6 we report our results on this version of the dataset as well, for which test set labels are unavailable. On ImageNet, it is customary to report two error rates: top-1 and top-5, where the top-5 error rate is the fraction of test images for which the correct label is not among the five labels considered most probable by the model.

　　ILSVRC-2010是ILSVRC竞赛中唯一可以获得测试集标签的版本，因此我们大多数实验都是在这个版本上运行的。由于我们也使用我们的模型参加了ILSVRC-2012竞赛，因此在第六节我们也报告了模型在这个版本的数据集上的结果，这个版本的测试标签是不可获得的。在ImageNet上，按照惯例报告两个错误率：top-1和top-5，top-5错误率是指测试图像的正确标签不在模型认为的五个最可能的便签之中的分数。

　　ImageNet consists of variable-resolution images, while our system requires a constant input dimensionality. Therefore, we down-sampled the images to a fixed resolution of 256 × 256. Given a rectangular image, we first rescaled the image such that the shorter side was of length 256, and then cropped out the central 256×256 patch from the resulting image. We did not pre-process the images in any other way, except for subtracting the mean activity over the training set from each pixel. So we trained our network on the (centered) raw RGB values of the pixels.

　　ImageNet包含各种分辨率的图像，而我们的系统要求固定的输入维度。因此，我们将图像进行下采样到固定的256×256分辨率。给定一个矩形图像，我们首先缩放图像短边长度为256，然后从结果图像中裁剪中心的256×256大小的图像块。除了在训练集上对像素减去平均活跃度外，我们不对图像做任何其它的预处理。因此我们在原始的RGB像素值（中心化的）上训练我们的网络。

3 The Architecture

　　The architecture of our network is summarized in Figure 2. It contains eight learned layers — five convolutional and three fully-connected. Below, we describe some of the novel or unusual features of our network’s architecture. Sections 3.1-3.4 are sorted according to our estimation of their importance, with the most important first.

3 架构

　　我们的网络架构概括为图2。它包含八个学习层——5个卷积层和3个全连接层。下面，我们将描述我们网络结构中的一些新奇的或者不寻常的特性。3.1-3.4小节按照我们对它们评估的重要性进行排序，最重要的排在最前面。

3.1 ReLU Nonlinearity

　　The standard way to model a neuron’s output f as a function of its input x is with f(x) = tanh(x) or f(x) = (1 + e^−x)⁻¹. In terms of training time with gradient descent, these saturating nonlinearities are much slower than the non-saturating nonlinearity f(x) = max(0,x). Following Nair and Hinton [20], we refer to neurons with this nonlinearity as Rectified Linear Units (ReLUs). Deep convolutional neural networks with ReLUs train several times faster than their equivalents with tanh units. This is demonstrated in Figure 1, which shows the number of iterations required to reach 25% training error on the CIFAR-10 dataset for a particular four-layer convolutional network. This plot shows that we would not have been able to experiment with such large neural networks for this work if we had used traditional saturating neuron models.

3.1 ReLU非线性

　　将神经元输出f建模为输入x的函数的标准方式是用f(x) = tanh(x)或f(x) = (1 + e^−x)⁻¹。考虑到梯度下降的训练时间，这些饱和的非线性比非饱和非线性f(x) = max(0,x)更慢。根据Nair和Hinton[20]的说法，我们将这种非线性神经元称为修正线性单元(ReLU)。采用ReLU的深度卷积神经网络训练时间比等价的tanh单元要快好几倍。在图1中，对于一个特定的四层卷积网络，在CIFAR-10数据集上达到25%的训练误差所需要的迭代次数可以证实这一点。这幅图表明，如果我们采用传统的饱和神经元模型，我们将不能在如此大的神经网络上实验该工作。

Figure 1: A four-layer convolutional neural network with ReLUs (solid line) reaches a 25% training error rate on CIFAR-10 six times faster than an equivalent network with tanh neurons (dashed line). The learning rates for each network were chosen independently to make training as fast as possible. No regularization of any kind was employed. The magnitude of the effect demonstrated here varies with network architecture, but networks with ReLUs consistently learn several times faster than equivalents with saturating neurons.

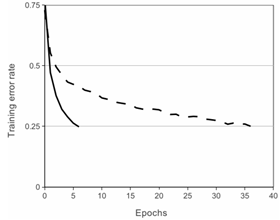
图1：使用ReLU的四层卷积神经网络在CIFAR-10数据集上达到25%的训练误差比使用tanh神经元的等价网络（虚线）快六倍。为了使训练尽可能快，每个网络的学习率是单独选择的。没有采用任何类型的正则化。影响的大小随着网络结构的变化而变化，这一点已得到证实，但使用ReLU的网络一直比等价的饱和神经元快几倍。

　　We are not the first to consider alternatives to traditional neuron models in CNNs. For example, Jarrett et al.[11] claim that the nonlinearity f(x) = |tanh(x)| works particularly well with their type of contrast normalization followed by local average pooling on the Caltech-101 dataset. However, on this dataset the primary concern is preventing overfitting, so the effect they are observing is different from the accelerated ability to fit the training set which we report when using ReLUs. Faster learning has a great influence on the performance of large models trained on large datasets.

　　我们不是第一个考虑替代CNN中传统神经元模型的人。例如，Jarrett等人[11]声称非线性函数f(x) = |tanh(x)|与对比归一化以及局部均值池化在Caltech-101数据集上表现甚好。然而，在这个数据集上主要的关注点是防止过拟合，因此他们观测到的影响（预防过拟合）不同于我们使用ReLU拟合数据集时的反映的加速能力。更快的学习速率对大型模型在大型数据集上的性能有很大的影响。

3.2 Training on Multiple GPUs

　　A single GTX 580 GPU has only 3GB of memory, which limits the maximum size of the networks that can be trained on it. It turns out that 1.2 million training examples are enough to train networks which are too big to fit on one GPU. Therefore we spread the net across two GPUs. Current GPUs are particularly well-suited to cross-GPU parallelization, as they are able to read from and write to one another’s memory directly, without going through host machine memory. The parallelization scheme that we employ essentially puts half of the kernels (or neurons) on each GPU, with one additional trick: the GPUs communicate only in certain layers. This means that, for example, the kernels of layer 3 take input from all kernel maps in layer 2. However, kernels in layer 4 take input only from those kernel maps in layer 3 which reside on the same GPU. Choosing the pattern of connectivity is a problem for cross-validation, but this allows us to precisely tune the amount of communication until it is an acceptable fraction of the amount of computation.

3.2 在多GPU上训练

　　单个GTX580 GPU只有3G内存，这限制了可以在GTX580上进行训练的网络最大尺寸。事实证明120万图像用来进行网络训练是足够的，但网络太大不能在单个GPU上进行训练。因此我们将网络分布在两个GPU上。目前的GPU非常适合跨GPU并行，因为它们可以直接互相读写内存，而不需要通过主机内存。我们采用的并行方案基本上每个GPU放置一半的核（或神经元），还有一个额外的技巧：只在某些特定的层上进行GPU通信。这意味着，例如，第3层的核会将第2层的所有核映射作为输入。然而，第4层的核只将位于相同GPU上的第3层的核映射作为输入。这种连接模式的选择有一个关于交叉验证的问题，但这可以让我们准确地调整通信数量，直到它的计算量在可接受的范围内。

　　The resultant architecture is somewhat similar to that of the “columnar” CNN employed by Ciresan et al.[5], except that our columns are not independent (see Figure 2). This scheme reduces our top-1 and top-5 error rates by 1.7% and 1.2%, respectively, as compared with a net with half as many kernels in each convolutional layer trained on one GPU. The two-GPU net takes slightly less time to train than the one-GPU net[2].

　　除了我们的列不是独立的之外（看图2），最终的架构有点类似于Ciresan等人[5]采用的“柱状”CNN。与每个卷积层中只有一半的核在单GPU上训练的网络相比，这个方案分别降低了我们的top-1 1.7%，top-5 1.2%的错误率。双GPU网络比单GPU网络稍微减少了训练时间²。

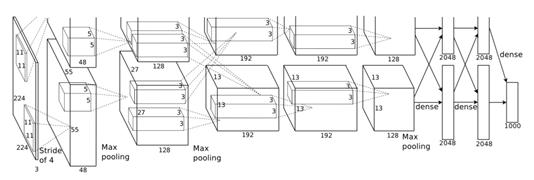
Figure 2: An illustration of the architecture of our CNN, explicitly showing the delineation of responsibilities between the two GPUs. One GPU runs the layer-parts at the top of the figure while the other runs the layer-parts at the bottom. The GPUs communicate only at certain layers. The network’s input is 150,528-dimensional, and the number of neurons in the network’s remaining layers is given by 253,440-186,624-64,896-64,896-43,264-4096-4096-1000.

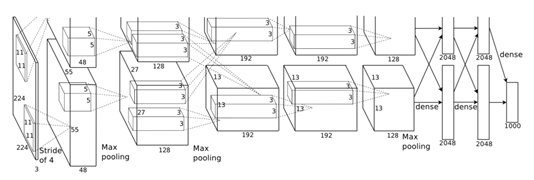图2：我们CNN架构图解，明确描述了两个GPU之间的职责。一个GPU运行图中上面部分的层，而另一个GPU运行图下面部分的层。两个GPU只在特定的层进行通信。网络的输入是150,528维，网络剩下层的神经元数目分别是253,440-186,624-64,896-64,896-43,264-4096-4096-1000。

3.3 Local Response Normalization

　　ReLUs have the desirable property that they do not require input normalization to prevent them from saturating. If at least some training examples produce a positive input to a ReLU, learning will happen in that neuron. However, we still find that the following local normalization scheme aids generalization. Denoting by  the activity of a neuron computed by applying kernel i at position (x,y) and then applying the ReLU nonlinearity, the response-normalized activity  given by the expression

 

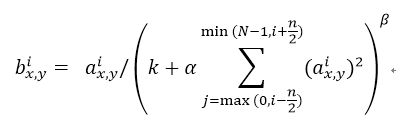
　　where the sum runs over n “adjacent” kernel maps at the same spatial position, and N is the total number of kernels in the layer. The ordering of the kernel maps is of course arbitrary and determined before training begins. This sort of response normalization implements a form of lateral inhibition inspired by the type found in real neurons, creating competition for big activities amongst neuron outputs computed using different kernels. The constants k, n, α, and β are hyper-parameters whose values are determined using a validation set; we used k = 2, n = 5, α = 0.0001, and β = 0.75. We applied this normalization after applying the ReLU nonlinearity in certain layers (see Section 3.5).

3.3 局部响应归一化

　　ReLU具有让人满意的特性，即它不需要通过输入归一化来防止饱和。如果至少一些训练样本对ReLU产生了正输入，那么那个神经元上将发生学习。然而，我们仍然发现接下来的局部归一化有助于泛化。 表示神经元激活，通过在(x,y)位置应用核i，然后应用ReLU非线性来计算，响应归一化激活 通过下式给定：

 

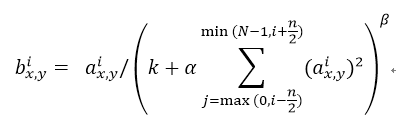
　　求和运算在n个“毗邻的”核映射的同一位置上执行，N是本层的卷积核数目。核映射的顺序当然是任意的，在训练开始前确定。响应归一化的顺序实现了一种侧抑制形式，灵感来自于真实神经元中发现的类型，为使用不同核进行神经元输出计算的较大活动创造了竞争。常量k，n，α，β是超参数，它们的值通过验证集确定；我们设k=2，n=5，α=0.0001，β=0.75。我们在特定的层使用的ReLU非线性之后应用了这种归一化（请看3.5小节）。

　　This scheme bears some resemblance to the local contrast normalization scheme of Jarrett et al.[11], but ours would be more correctly termed “brightness normalization”, since we do not subtract the mean activity. Response normalization reduces our top-1 and top-5 error rates by 1.4% and 1.2%, respectively. We also verified the effectiveness of this scheme on the CIFAR-10 dataset: a four-layer CNN achieved a 13% test error rate without normalization and 11% with normalization[3].

　　这个方案与Jarrett等人[11]的局部对比度归一化方案有一定的相似性，但我们更恰当的称其为“亮度归一化”，因为我们没有减去均值。响应归一化分别减少了top-1 1.4%，top-5 1.2%的错误率。我们也在CIFAR-10数据集上验证了这个方案的有效性：没有归一化的四层CNN取得了13%的错误率，而使用归一化取得了11%的错误率³。

3.4 Overlapping Pooling

　　Pooling layers in CNNs summarize the outputs of neighboring groups of neurons in the same kernel map. Traditionally, the neighborhoods summarized by adjacent pooling units do not overlap (e.g., [17, 11, 4]). To be more precise, a pooling layer can be thought of as consisting of a grid of pooling units spaced s pixels apart, each summarizing a neighborhood of size z × z centered at the location of the pooling unit. If we set s = z, we obtain traditional local pooling as commonly employed in CNNs. If we set s < z, we obtain overlapping pooling. This is what we use throughout our network, with s = 2 and z = 3. This scheme reduces the top-1 and top-5 error rates by 0.4% and 0.3%, respectively, as compared with the non-overlapping scheme s = 2, z = 2, which produces output of equivalent dimensions. We generally observe during training that models with overlapping pooling find it slightly more difficult to overfit.

3.4 重叠池化

　　CNN中的池化层使用相同的核映射归纳了神经元相邻组的输出。习惯上，相邻池化单元归纳的区域是不重叠的（例如[17, 11, 4]）。更确切的说，池化层可看作由池化单元网格组成，网格间距为s个像素，每个网格归纳池化单元中心位置z × z大小的邻居。如果设置s = z，我们会得到通常在CNN中采用的传统局部池化。如果设置s < z，我们会得到重叠池化。这就是我们网络中使用的方法，设置s = 2，z = 3。这个方案与非重叠方案s = 2, z = 2相比，分别降低了top-1 0.4%，top-5 0.3%的错误率，两者的输出维度是相等的。我们在训练过程发现，采用重叠池化的模型更难以过拟合。

3.5 Overall Architecture

　　Now we are ready to describe the overall architecture of our CNN. As depicted in Figure 2, the net contains eight layers with weights; the first five are convolutional and the remaining three are fully-connected. The output of the last fully-connected layer is fed to a 1000-way softmax which produces a distribution over the 1000 class labels. Our network maximizes the multinomial logistic regression objective, which is equivalent to maximizing the average across training cases of the log-probability of the correct label under the prediction distribution.

3.5 整体架构

　　现在我们准备描述我们的CNN的整体架构。如图2所示，我们的网络包含8个带权重的层；前5层是卷积层，剩下的3层是全连接层。最后一层全连接层的输出喂给1000维的softmax层，softmax会产生1000类标签的分布。我们的网络最大化多项逻辑回归的目标，这等价于最大化预测分布下训练样本正确标签的对数概率的均值。

　　The kernels of the second, fourth, and fifth convolutional layers are connected only to those kernel maps in the previous layer which reside on the same GPU (see Figure 2). The kernels of the third convolutional layer are connected to all kernel maps in the second layer. The neurons in the fully-connected layers are connected to all neurons in the previous layer. Response-normalization layers follow the first and second convolutional layers. Max-pooling layers, of the kind described in Section 3.4, follow both response-normalization layers as well as the fifth convolutional layer. The ReLU non-linearity is applied to the output of every convolutional and fully-connected layer.

　　第2，4，5卷积层的神经元只与位于同一GPU上的前一层的核映射相连接（见图2）。第3卷积层的核与第2层的所有核映射相连。全连接层的神经元与前一层的所有神经元相连。第1，2卷积层之后是响应归一化层。第3.4节描述的这种最大池化层加在了响应归一化层和第5卷积层之后。ReLU非线性应用在每个卷积层和全连接层的输出上。

　　The first convolutional layer filters the 224 × 224 × 3 input image with 96 kernels of size 11 × 11 × 3 with a stride of 4 pixels (this is the distance between the receptive field centers of neighboring neurons in a kernel map). The second convolutional layer takes as input the (response-normalized and pooled) output of the first convolutional layer and filters it with 256 kernels of size 5 × 5 × 48. The third, fourth, and fifth convolutional layers are connected to one another without any intervening pooling or normalization layers. The third convolutional layer has 384 kernels of size 3 × 3 × 256 connected to the (normalized, pooled) outputs of the second convolutional layer. The fourth convolutional layer has 384 kernels of size 3 × 3 × 192 , and the fifth convolutional layer has 256 kernels of size 3 × 3 × 192. The fully-connected layers have 4096 neurons each.

　　第1卷积层使用96个核对224 × 224 × 3的输入图像进行滤波操作，核大小为11 × 11 × 3，步长是4个像素（核映射中相邻神经元感受野中心之间的距离）。第2卷积层使用第1卷积层的输出（响应归一化和池化）作为输入，并使用256个大小为5 × 5 × 48核进行滤波。第3，4，5卷积层依次连接，中间没有接入任何池化层或归一化层。第3卷积层有384个大小为3 × 3 × 256的核，与第2卷积层的输出（归一化的，池化的）相连。第4卷积层有384个大小为3 × 3 × 192的核，第5卷积层有256个核大小为3 × 3 × 192的核。每个全连接层有4096个神经元。

4 Reducing Overfitting

　　Our neural network architecture has 60 million parameters. Although the 1000 classes of ILSVRC make each training example impose 10 bits of constraint on the mapping from image to label, this turns out to be insufficient to learn so many parameters without considerable overfitting. Below, we describe the two primary ways in which we combat overfitting.

4 减少过拟合

　　我们的神经网络架构有6000万参数。尽管ILSVRC的1000类使每个训练样本从图像到标签的映射上强加了10比特的约束，但这不足以学习这么多的参数而没有相当大的过拟合。下面，我们会描述我们用来克服过拟合的两种主要方式。

4.1 Data Augmentation

　　The easiest and most common method to reduce overfitting on image data is to artificially enlarge the dataset using label-preserving transformations (e.g., [25, 4, 5]). We employ two distinct forms of data augmentation, both of which allow transformed images to be produced from the original images with very little computation, so the transformed images do not need to be stored on disk. In our implementation, the transformed images are generated in Python code on the CPU while the GPU is training on the previous batch of images. So these data augmentation schemes are, in effect, computationally free.

4.1 数据增强

　　图像数据上最简单常用的用来减少过拟合的方法是使用标签保留变换（例如[25, 4, 5]）来人工增大数据集。我们使用了两种不同的数据增强方式，这两种方式都是从原始图像通过非常少的计算量产生变换的图像，因此变换图像不需要存储在硬盘上。在我们的实现中，变换图像通过CPU的Python代码生成，而此时GPU正在训练前一批图像。因此，实际上这些数据增强方案没有消耗计算量。

　　The first form of data augmentation consists of generating image translations and horizontal reflections. We do this by extracting random 224 × 224 patches (and their horizontal reflections) from the 256×256 images and training our network on these extracted patches[4]. This increases the size of our training set by a factor of 2048, though the resulting training examples are, of course, highly interdependent. Without this scheme, our network suffers from substantial overfitting, which would have forced us to use much smaller networks. At test time, the network makes a prediction by extracting five 224 × 224 patches (the four corner patches and the center patch) as well as their horizontal reflections (hence ten patches in all), and averaging the predictions made by the network’s softmax layer on the ten patches.

　　第一种数据增强方式包括产生图像平移和水平翻转。我们从256× 256图像上通过随机提取224 × 224的图像块（以及这些图像块的水平翻转）实现了这种方式，然后在这些提取的图像块上进行训练⁴。这通过一个2048因子增大了我们的训练集，尽管最终的训练样本是高度相关的。没有这个方案，我们的网络会有大量的过拟合，这会迫使我们使用更小的网络。在测试时，网络会提取5个224 × 224的图像块（四个角上的图像块和中心的图像块）和它们的水平翻转（因此总共10个图像块）进行预测，然后对网络在10个图像块上的softmax层的预测结果进行平均。

　　The second form of data augmentation consists of altering the intensities of the RGB channels in training images. Specifically, we perform PCA on the set of RGB pixel values throughout the ImageNet training set. To each training image, we add multiples of the found principal components, with magnitudes proportional to the corresponding eigenvalues times a random variable drawn from a Gaussian with mean zero and standard deviation 0.1. Therefore to each RGB image pixel  we add the following quantity:

 

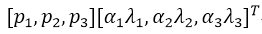
　　where p_i and λ_i are ith eigenvector and eigenvalue of the 3 × 3 covariance matrix of RGB pixel values, respectively, and α_i is the aforementioned random variable. Each α_i is drawn only once for all the pixels of a particular training image until that image is used for training again, at which point it is re-drawn. This scheme approximately captures an important property of natural images, namely, that object identity is invariant to changes in the intensity and color of the illumination. This scheme reduces the top-1 error rate by over 1%.

　　第二种数据增强方式包括改变训练图像的RGB通道的强度。具体地，我们在整个ImageNet训练集上对RGB像素值集合执行主成分分析（PCA）。对于每幅训练图像，我们加上多倍找到的主成分，大小成正比的对应特征值乘以一个随机变量，随机变量通过均值为0，标准差为0.1的高斯分布得到。因此对于每幅RGB图像像素 ，我们加上下面的数量：

 

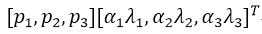
　　p_i，λ_i分别是RGB像素值3 × 3协方差矩阵的第i个特征向量和特征值，α_i是前面提到的随机变量。对于某个训练图像的所有像素，每个α_i只获取一次，直到图像进行下一次训练时才重新获取。这个方案近似抓住了自然图像的一个重要特性，即光照的强度和颜色发生变化时，物体本身没有发生变化。这个方案减少了top 1错误率1%以上。

4.2 Dropout

　　Combining the predictions of many different models is a very successful way to reduce test errors [1, 3], but it appears to be too expensive for big neural networks that already take several days to train. There is, however, a very efficient version of model combination that only costs about a factor of two during training. The recently-introduced technique, called “dropout”[10], consists of setting to zero the output of each hidden neuron with probability 0.5. The neurons which are “dropped out” in this way do not contribute to the forward pass and do not participate in back-propagation. So every time an input is presented, the neural network samples a different architecture, but all these architectures share weights. This technique reduces complex co-adaptations of neurons, since a neuron cannot rely on the presence of particular other neurons. It is, therefore, forced to learn more robust features that are useful in conjunction with many different random subsets of the other neurons. At test time, we use all the neurons but multiply their outputs by 0.5, which is a reasonable approximation to taking the geometric mean of the predictive distributions produced by the exponentially-many dropout networks.

4.2 丢弃（Dropout）

　　将许多不同模型的预测结果结合起来是降低测试误差[1, 3]的一个非常成功的方法，但对于需要花费几天来训练的大型神经网络来说，这似乎将花费太长时间以至于无法训练。然而，有一个非常有效的模型结合版本，它只花费两倍的训练成本。这种最近推出的技术，叫做“dropout”[10]，它会以0.5的概率对每个隐层神经元的输出设为0。那些用这种方式“丢弃”的神经元不再进行前向传播并且不参与反向传播。因此每次输入时，神经网络会采样一个不同的架构，但所有架构共享权重。这个技术减少了复杂的神经元互适应，因为一个神经元不能依赖特定的其它神经元的存在。因此，神经元被强迫学习更鲁棒的特征，它在与许多不同的其它神经元的随机子集结合时是有用的。在测试时，我们使用所有的神经元但它们的输出乘以0.5，对指数级的许多失活网络的预测分布进行几何平均，这是一种合理的近似。

　　We use dropout in the first two fully-connected layers of Figure 2. Without dropout, our network exhibits substantial overfitting. Dropout roughly doubles the number of iterations required to converge.

　　我们在图2中的前两个全连接层使用失活。如果没有失活，我们的网络表现出大量的过拟合。失活大致上使要求收敛的迭代次数翻了一倍。

5 Details of learning

　　We trained our models using stochastic gradient descent with a batch size of 128 examples, momentum of 0.9, and weight decay of 0.0005. We found that this small amount of weight decay was important for the model to learn. In other words, weight decay here is not merely a regularizer: it reduces the model’s training error. The update rule for weight w was

 

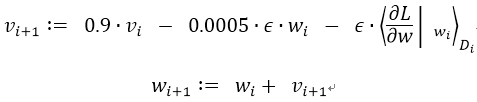
　　where i is the iteration index, v is the momentum variable, ϵ is the learning rate, and is the average over the ith batch D_i of the derivative of the objective with respect to w, evaluated at w_i.

5 学习细节

　　我们使用随机梯度下降来训练我们的模型，样本的batch size为128，动量为0.9，权重衰减率为0.0005。我们发现少量的权重衰减对于模型的学习是重要的。换句话说，权重衰减不仅仅是一个正则项：而且它减少了模型的训练误差。权重ww的更新规则是：

 

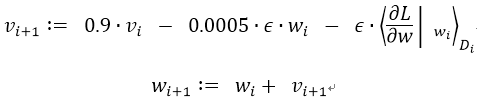
　　i是迭代索引，v是动量变量，ϵ是学习率， 是目标函数对w，在w_i上的第i批微分D_i的平均。

　　We initialized the weights in each layer from a zero-mean Gaussian distribution with standard deviation 0.01. We initialized the neuron biases in the second, fourth, and fifth convolutional layers, as well as in the fully-connected hidden layers, with the constant 1. This initialization accelerates the early stages of learning by providing the ReLUs with positive inputs. We initialized the neuron biases in the remaining layers with the constant 0.

　　我们使用均值为0，标准差为0.01的高斯分布对每一层的权重进行初始化。我们在第2，4，5卷积层和全连接隐层将神经元偏置初始化为常量1。这个初始化通过为ReLU提供正输入加速了早期阶段的学习。我们对剩下的层的神经元偏置初始化为0。

　　We used an equal learning rate for all layers, which we adjusted manually throughout training. The heuristic which we followed was to divide the learning rate by 10 when the validation error rate stopped improving with the current learning rate. The learning rate was initialized at 0.01 and reduced three times prior to termination. We trained the network for roughly 90 cycles through the training set of 1.2 million images, which took five to six days on two NVIDIA GTX 580 3GB GPUs.

　　我们对所有的层使用相等的学习率，这个是在整个训练过程中我们手动调整得到的。当验证误差在当前的学习率下停止改善时，我们遵循启发式的方法将学习率除以10。学习率初始化为0.01，在训练停止之前降低三次。我们在120万图像的训练数据集上训练神经网络大约90个循环，在两个NVIDIA GTX 580 3GB GPU上花费了五到六天。

6 Results

　　Our results on ILSVRC-2010 are summarized in Table 1. Our network achieves top-1 and top-5 test set error rates of 37.5% and 17.0%[5]. The best performance achieved during the ILSVRC-2010 competition was 47.1% and 28.2% with an approach that averages the predictions produced from six sparse-coding models trained on different features [2], and since then the best published results are 45.7% and 25.7% with an approach that averages the predictions of two classifiers trained on Fisher Vectors (FVs) computed from two types of densely-sampled features [24].

 

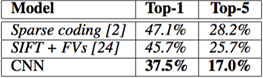
Table 1: Comparison of results on ILSVRC-2010 test set. In italics are best results achieved by others.

6 结果

　　我们在ILSVRC-2010上的结果概括为表1。我们的神经网络取得了top-1 37.5%，top-5 17.0%的错误率⁵。在ILSVRC-2010竞赛中最佳结果是top-1错误率47.1%和top-5错误率28.2%，使用的方法是对6个在不同特征上训练的稀疏编码模型生成的预测进行平均，之后公布的最好结果是top-1错误率45.7%和top-5错误率25.7%，使用的方法是在Fisher向量（FV）上训练的两个分类器的预测结果取平均，Fisher向量是通过两种密集采样特征计算得到的[24]。

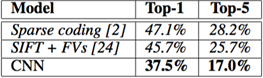
表1：ILSVRC-2010测试集上的结果对比。斜体表示的是其它人取得的最好结果。

　　We also entered our model in the ILSVRC-2012 competition and report our results in Table 2. Since the ILSVRC-2012 test set labels are not publicly available, we cannot report test error rates for all the models that we tried. In the remainder of this paragraph, we use validation and test error rates interchangeably because in our experience they do not differ by more than 0.1% (see Table 2). The CNN described in this paper achieves a top-5 error rate of 18.2%. Averaging the predictions of five similar CNNs gives an error rate of 16.4%. Training one CNN, with an extra sixth convolutional layer over the last pooling layer, to classify the entire ImageNet Fall 2011 release (15M images, 22K categories), and then “fine-tuning” it on ILSVRC-2012 gives an error rate of 16.6%. Averaging the predictions of two CNNs that were pre-trained on the entire Fall 2011 release with the aforementioned five CNNs gives an error rate of 15.3%. The second-best contest entry achieved an error rate of 26.2% with an approach that averages the predictions of several classifiers trained on FVs computed from different types of densely-sampled features [7].

Table 2: Comparison of error rates on ILSVRC-2012 validation and test sets. In italics are best results achieved by others. Models with an asterisk were “pre-trained” to classify the entire ImageNet 2011 Fall release. See Section 6 for details.

　　我们也用我们的模型参加了ILSVRC-2012竞赛并在表2中报告了我们的结果。由于ILSVRC-2012的测试集标签没有公开，因此我们不能报告我们尝试的所有模型的测试错误率。在这段的其余部分，我们会将验证误差率和测试误差率互换，因为在我们的实验中它们的差别不会超过0.1%（看图2）。本文中描述的CNN取得了top-5 18.2%的错误率。五个类似的CNN预测的平均误差率为16.4%。为了对ImageNet 2011秋季发布的整个数据集（1500万图像，22000个类别）进行分类，我们在最后的池化层之后有一个额外的第6卷积层，训练了一个CNN，然后在它上面进行“微调”，在ILSVRC-2012取得了16.6%的错误率。对在ImageNet 2011秋季发布的整个数据集上预训练的两个CNN和前面提到的五个CNN的预测进行平均得到了15.3%的错误率。第二名的最好竞赛团队取得了26.2%的错误率，他的方法是对FV上训练的一些分类器的预测结果进行平均，FV在不同类型密集采样特征计算得到的。

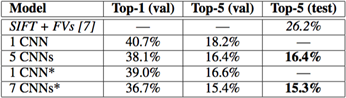
表2：ILSVRC-2012验证集和测试集的误差对比。斜线部分是其它人取得的最好的结果。带星号的是“预训练的”对ImageNet 2011秋季数据集进行分类的模型。更多细节请看第六节。

　　Finally, we also report our error rates on the Fall 2009 version of ImageNet with 10,184 categories and 8.9 million images. On this dataset we follow the convention in the literature of using half of the images for training and half for testing. Since there is no established test set, our split necessarily differs from the splits used by previous authors, but this does not affect the results appreciably. Our top-1 and top-5 error rates on this dataset are 67.4% and 40.9%, attained by the net described above but with an additional, sixth convolutional layer over the last pooling layer. The best published results on this dataset are 78.1% and 60.9% [19].

　　最后，我们也报告了我们在ImageNet 2009秋季数据集上的错误率，ImageNet 2009秋季数据集有10,184个类，890万图像。在这个数据集上我们按照文献中的惯例，用一半的图像来训练，一半的图像来测试。由于数据集上没有建立好的测试集，我们对数据集分割必然不同于以前作者的数据集分割，但这对结果没有明显的影响。我们在这个数据集上的的top-1和top-5错误率是67.4%和40.9%，使用的是上面描述的在最后的池化层之后有一个额外的第6卷积层网络。这个数据集上公开可获得的top-1和top-5错误率最好结果是78.1%和60.9%[19]。

6.1 Qualitative Evaluations

　　Figure 3 shows the convolutional kernels learned by the network’s two data-connected layers. The network has learned a variety of frequency and orientation-selective kernels, as well as various colored blobs. Notice the specialization exhibited by the two GPUs, a result of the restricted connectivity described in Section 3.5. The kernels on GPU 1 are largely color-agnostic, while the kernels on on GPU 2 are largely color-specific. This kind of specialization occurs during every run and is independent of any particular random weight initialization (modulo a renumbering of the GPUs).

Figure 3: 96 convolutional kernels of size 11×11×3 learned by the first convolutional layer on the 224×224×3 input images. The top 48 kernels were learned on GPU 1 while the bottom 48 kernels were learned on GPU 2. See Section 6.1 for details.

6.1 定性评估

　　图3显示了网络的两个数据连接层学习到的卷积核。网络学习到了大量的频率核、方向选择核，也学到了各种颜色点。注意两个GPU表现出的专业化，3.5小节中描述的受限连接的结果。GPU 1上的核主要是没有颜色的，而GPU 2上的核主要是针对颜色的。这种专业化在每次运行时都会发生，并且是与任何特别的随机权重初始化（以GPU的重新编号为模）无关的。

图3：第一卷积层在224×224×3的输入图像上学习到的大小为11×11×3的96个卷积核。上面的48个核是在GPU 1上学习到的而下面的48个卷积核是在GPU 2上学习到的。更多细节请看6.1小节。

　　In the left panel of Figure 4 we qualitatively assess what the network has learned by computing its top-5 predictions on eight test images. Notice that even off-center objects, such as the mite in the top-left, can be recognized by the net. Most of the top-5 labels appear reasonable. For example, only other types of cat are considered plausible labels for the leopard. In some cases (grille, cherry) there is genuine ambiguity about the intended focus of the photograph.

   

Figure 4: (Left) Eight ILSVRC-2010 test images and the five labels considered most probable by our model. The correct label is written under each image, and the probability assigned to the correct label is also shown with a red bar (if it happens to be in the top 5). (Right) Five ILSVRC-2010 test images in the first column. The remaining columns show the six training images that produce feature vectors in the last hidden layer with the smallest Euclidean distance from the feature vector for the test image.

　　在图4的左边部分，我们通过在8张测试图像上计算它的top-5预测定性地评估了网络学习到的东西。注意即使不在图像中心的目标也能被网络识别，例如左上角的小虫。大多数的top-5标签似乎是合理的。例如，对于美洲豹来说，只有其它类型的猫被认为是看似合理的标签。在某些案例（格栅，樱桃）中，照片的预期焦点确实存在的模糊性。。

    

图4：（左）8张ILSVRC-2010测试图像和我们的模型认为最可能的5个标签。每张图像的下面是它的正确标签，正确标签的概率用红色柱形表示（如果正确标签在top 5中）。（右）第一列是5张ILSVRC-2010测试图像。剩下的列展示了6张训练图像，这些图像在最后的隐藏层的特征向量与测试图像的特征向量有最小的欧氏距离。

　　Another way to probe the network’s visual knowledge is to consider the feature activations induced by an image at the last, 4096-dimensional hidden layer. If two images produce feature activation vectors with a small Euclidean separation, we can say that the higher levels of the neural network consider them to be similar. Figure 4 shows five images from the test set and the six images from the training set that are most similar to each of them according to this measure. Notice that at the pixel level, the retrieved training images are generally not close in L2 to the query images in the first column. For example, the retrieved dogs and elephants appear in a variety of poses. We present the results for many more test images in the supplementary material.

　　探索网络可视化知识的另一种方式是思考最后的4096维隐藏层在图像上得到的特征激活。如果两幅图像生成的特征激活向量之间有较小的欧式距离，我们可以认为神经网络的更高层特征认为它们是相似的。图4表明根据这个度量标准，测试集的5张图像和训练集的6张图像中的每一张都是最相似的。注意在像素级别，检索到的训练图像与第一列的查询图像在L2上通常是不接近的。例如，检索的狗和大象似乎有不同的姿态。我们在补充材料中对更多的测试图像呈现了这种结果。

　　Computing similarity by using Euclidean distance between two 4096-dimensional, real-valued vectors is inefficient, but it could be made efficient by training an auto-encoder to compress these vectors to short binary codes. This should produce a much better image retrieval method than applying auto-encoders to the raw pixels [14], which does not make use of image labels and hence has a tendency to retrieve images with similar patterns of edges, whether or not they are semantically similar.

　　通过两个4096维实值向量间的欧氏距离来计算相似性是效率低下的，但通过训练一个自动编码器将这些向量压缩为短二值编码可以使其变得高效。这应该会产生一种比将自动编码器应用到原始像素上[14]更好的图像检索方法，自动编码器应用到原始像素上的方法没有使用图像标签，因此会趋向于检索与要检索的图像具有相似边缘模式的图像，无论它们是否是语义上相似。

7 Discussion

　　Our results show that a large, deep convolutional neural network is capable of achieving record-breaking results on a highly challenging dataset using purely supervised learning. It is notable that our network’s performance degrades if a single convolutional layer is removed. For example, removing any of the middle layers results in a loss of about 2% for the top-1 performance of the network. So the depth really is important for achieving our results.

7 讨论

　　我们的结果表明一个大型深度卷积神经网络在一个具有高度挑战性的数据集上使用纯有监督学习可以取得破纪录的结果。值得注意的是，如果移除任何一个卷积层，我们的网络性能会降低。例如，移除任何中间层都会引起网络损失大约2%的top-1性能。因此深度对于实现我们的结果非常重要。

　　To simplify our experiments, we did not use any unsupervised pre-training even though we expect that it will help, especially if we obtain enough computational power to significantly increase the size of the network without obtaining a corresponding increase in the amount of labeled data. Thus far, our results have improved as we have made our network larger and trained it longer but we still have many orders of magnitude to go in order to match the infero-temporal pathway of the human visual system. Ultimately we would like to use very large and deep convolutional nets on video sequences where the temporal structure provides very helpful information that is missing or far less obvious in static images.

　　为了简化我们的实验，我们没有使用任何无监督的预训练，尽管我们希望它会有所帮助，特别是在如果我们能获得足够的计算能力来显著增加网络的大小而标注的数据量没有对应增加的情况下。到目前为止，我们的结果已经提高了，因为我们的网络更大、训练时间更长，但为了匹配人类视觉系统的下颞线（视觉专业术语）我们仍然有许多数量级要达到。最后我们想在视频序列上使用非常大的深度卷积网络，视频序列的时序结构会提供非常有帮助的信息，这些信息在静态图像上是缺失的或远不那么明显。

References

参考文献

[1] R. M. Bell and Y. Koren. Lessons from the Netflix prize challenge. ACMSIGKDD Explorations Newsletter, 9(2):75–79, 2007.

[2] A. Berg, J. Deng, and L. Fei-Fei. Large scale visual recognition challenge 2010. www.imagenet.org/challenges. 2010.

[3] L. Breiman. Random forests. Machine learning, 45(1):5–32, 2001.

[4] D. Cires ̧an, U. Meier, and J. Schmidhuber. Multi-column deep neural networks for image classification. Arxiv preprint arXiv:1202.2745, 2012.

[5] D.C. Cires ̧an, U. Meier, J. Masci, L.M. Gambardella, and J. Schmidhuber. High-performance neural networks for visual object classification. Arxiv preprint arXiv:1102.0183, 2011.

[6] J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. Fei-Fei. ImageNet: A Large-Scale Hierarchical Image Database. In CVPR09, 2009.

[7] J. Deng, A. Berg, S. Satheesh, H. Su, A. Khosla, and L. Fei-Fei. ILSVRC-2012, 2012. URL http://www.image-net.org/challenges/LSVRC/2012/.

[8] L. Fei-Fei, R. Fergus, and P. Perona. Learning generative visual models from few training examples: An incremental bayesian approach tested on 101 object categories. Computer Vision and Image Understanding, 106(1):59–70, 2007.

[9] G. Griffin, A. Holub, and P. Perona. Caltech-256 object category dataset. Technical Report 7694, California Institute of Technology, 2007. URL http://authors.library.caltech.edu/7694.

[10] G.E. Hinton, N. Srivastava, A. Krizhevsky, I. Sutskever, and R.R. Salakhutdinov. Improving neural networks by preventing co-adaptation of feature detectors. arXiv preprint arXiv:1207.0580, 2012.

[11] K. Jarrett, K. Kavukcuoglu, M. A. Ranzato, and Y. LeCun. What is the best multi-stage architecture for object recognition? In International Conference on Computer Vision, pages 2146–2153. IEEE, 2009.

[12] A. Krizhevsky. Learning multiple layers of features from tiny images. Master’s thesis, Department of Computer Science, University of Toronto, 2009.

[13] A. Krizhevsky. Convolutional deep belief networks on cifar-10. Unpublished manuscript, 2010.

[14] A. Krizhevsky and G.E. Hinton. Using very deep autoencoders for content-based image retrieval. In ESANN, 2011.

[15] Y. Le Cun, B. Boser, J.S. Denker, D. Henderson, R.E. Howard, W. Hubbard, L.D. Jackel, et al. Handwritten digit recognition with a back-propagation network. In Advances in neural information processing systems, 1990.

[16] Y. LeCun, F.J. Huang, and L. Bottou. Learning methods for generic object recognition with invariance to pose and lighting. In Computer Vision and Pattern Recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE Computer Society Conference on, volume 2, pages II–97. IEEE, 2004.

[17] Y. LeCun, K. Kavukcuoglu, and C. Farabet. Convolutional networks and applications in vision. In Circuits and Systems (ISCAS), Proceedings of 2010 IEEE International Symposium on, pages 253–256. IEEE, 2010.

[18] H. Lee, R. Grosse, R. Ranganath, and A.Y. Ng. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In Proceedings of the 26th Annual International Conference on Machine Learning, pages 609–616. ACM, 2009.

[19] T. Mensink, J. Verbeek, F. Perronnin, and G. Csurka. Metric Learning for Large Scale Image Classification: Generalizing to New Classes at Near-Zero Cost. In ECCV - European Conference on Computer Vision, Florence, Italy, October 2012.

[20] V. Nair and G. E. Hinton. Rectified linear units improve restricted boltzmann machines. In Proc. 27th International Conference on Machine Learning, 2010.

[21] N. Pinto, D.D. Cox, and J.J. DiCarlo. Why is real-world visual object recognition hard? PLoS computational biology, 4(1):e27, 2008.

[22] N. Pinto, D. Doukhan, J.J. DiCarlo, and D.D. Cox. A high-throughput screening approach to discovering good forms of biologically inspired visual representation. PLoS computational biology, 5(11):e1000579,2009.

[23] B.C. Russell, A. Torralba, K.P. Murphy, and W.T. Freeman. Labelme: a database and web-based tool for image annotation. International journal of computer vision, 77(1):157–173, 2008.

[24] J. Sánchezand F. Perronnin. High-dimensional signature compression for large-scale image classification. In Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on, pages 1665–1672. IEEE,2011.

[25] P.Y. Simard, D. Steinkraus, and J.C. Platt. Best practices for convolutional neural networks applied to visual document analysis. In Proceedings of the Seventh International Conference on Document Analysis and Recognition, volume 2, pages 958–962, 2003.

[26] S. C. Turaga, J. F. Murray, V. Jain, F. Roth, M. Helmstaedter, K. Briggman, W. Denk, and H. S. Seung. Convolutional networks can learn to generate affinity graphs for image segmentation. Neural Computation, 22(2):511–538, 2010.

 

论文脚注：

Communication-Efficient Learning of Deep Networks from Decentralized Data

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

 

Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS) 2017, Fort Lauderdale, Florida, USA. JMLR: W&CP volume 54. Copyright 2017 by the author(s).

 

 

Abstract

　　现代移动设备可以访问大量适合模型学习的数据，从而大大改善设备上的用户体验。例如，语言模型可以改善语音识别和文本输入，图像模型可以自动选择好的照片。然而，这些丰富的数据往往对隐私敏感，数量庞大，或者两者兼而有之，这可能会妨碍登录到数据中心并使用传统方法进行训练。我们提倡一种替代方法，将训练数据分布在移动设备上，并通过聚集本地计算的更新来学习共享模型。我们将这种去中心化的方法称为联邦学习。我们提出了一种基于迭代模型平均的深度网络联邦学习的实用方法，并对五种不同的模型结构和四种数据集进行了广泛的实证评估。这些实验表明，该方法对不平衡和非独立同分布（non-IID）的数据分布具有鲁棒性，这是该设置的一个定义特征。通信成本是主要的限制条件，与同步随机梯度下降相比，我们所需的通信轮数减少了10–100倍。

 

1　　Introduction

　　手机和平板电脑日益成为许多人的主要计算设备[30，2]。这些设备（包括摄像头、麦克风和GPS）上强大的传感器，再加上它们经常被携带，意味着它们能够获得前所未有的数据量，其中大部分数据是私有的。在这些数据上学习到的模型有希望通过驱动更智能的应用程序来大大提高可用性，但数据的敏感性意味着将其集中存储存在风险和责任。

　　我们研究了一种学习技术，它允许用户在不需要集中存储数据的情况下，从这些丰富的数据中获得共享模型的好处。因为学习任务是通过一个由中央服务器协调的参与设备（我们称之为客户机）的松散联合来解决的，所以我们称之为联邦学习。每个客户机都有一个从未上载到服务器的本地训练数据集。相反，每个客户机对由服务器维护的当前全局模型进行更新计算，并且只传递此更新到服务器。这是对《2012年白宫消费者数据隐私报告》提出的集中收集或数据最小化原则的直接应用[39]。由于这些更新是专门用于改进当前模型的，因此没有理由在应用后进行存储。

　　这种方法的一个主要优点是将模型训练与直接访问原始训练数据的需求分离开来。显然，负责协调训练的服务器仍然需要一些信任。但是，对于可以根据每个客户端上可用的数据指定训练目标的应用程序，联邦学习可以通过将攻击面仅限于设备，而不是设备和云，来显著降低隐私和安全风险。

　　我们的主要贡献是：1）将移动设备分散数据训练问题，作为一个重要的研究方向；2）选择出了一种可应用于此设置的简单实用的算法；3）对提出的方法进行了广泛的实证评估。更具体地说，我们引入了联邦平均（FederatedAveraging）算法，它将每个客户机上的局部随机梯度下降（SGD）与执行模型平均的服务器相结合。我们对该算法进行了大量的实验，证明了该算法对不平衡和非IID数据分布的鲁棒性，并能将在分散数据上训练深度网络所需的通信次数减少若干个数量级。

 

Federated Learning　　联邦学习的理想问题具有以下特性：1）对来自移动设备的真实数据进行训练比对数据中心中通常提供的代理数据进行训练具有明显的优势。2）此数据对隐私敏感或大小较大（与模型的大小相比），因此最好不要仅出于模型训练（服务于集中收集原则）的目的将其记录到数据中心。3）对于有监督的任务，数据上的标签可以从用户交互中自然推断出来。

　　许多支持移动设备智能行为的模型都符合上述标准。作为两个例子，我们考虑了图像分类，例如预测哪些照片在未来最可能被多次查看或共享；以及语言模型，通过改进解码、预测下一个单词，甚至预测整个回复[10]来改进触摸屏键盘上的语音识别和文本输入。这两项任务的潜在训练数据（用户拍摄的所有照片以及他们在移动键盘上键入的所有内容，包括密码、URLs、消息等）可能对隐私敏感。这些示例的分布也可能与容易获得的代理数据集有很大的不同：在聊天和文本消息中使用的语言通常与标准语言语料库（如维基百科和其他Web文档）有很大的不同；人们拍摄在他们手机上的的照片可能与典型的Flickr照片大不相同。最后，这些问题的标签是直接可用的；输入的文本是用于语言模型学习的自我标签，照片标签可以通过用户与他们的照片应用程序的自然交互来定义（哪些照片是删除、共享或查看的）。

　　这两项任务都非常适合神经网络学习。对于图像分类任务，前馈深度网络，尤其是在特定的卷积网络，能够提供最先进的结果[26，25]。对于语言建模任务，递归神经网络，尤其是LSTMs，已经取得了最先进的结果[20，5，22]。

 

Privacy　　与数据中心对持久数据的训练相比，联邦学习具有明显的隐私优势。即使拥有一个“匿名”的数据集，通过与其他数据的连接，仍然会使用户隐私受到威胁[37]。相比之下，联邦学习传输的信息是改进特定模型所必需的最小更新（自然地，隐私获益的强度取决于更新的内容）。更新本身可以（并且应该）是短暂的。它们永远不会包含比原始训练数据更多的信息（由于数据处理的不平等），而且通常包含的信息要少得多。此外，聚合算法不需要更新的来源，因此可以在不识别元数据的情况下通过混合网络（如Tor[7]）或受信任的第三方传输更新。本文最后简要讨论了联邦学习与安全多方计算和差异隐私相结合的可能性。

 

Federated Optimization　　我们将联邦学习中隐含的优化问题称为联邦优化，并与分布式优化建立了联系（和对比）。联合优化有几个关键特性，可以将其与典型的分布式优化问题区分开来：

• 非独立同分布：给定客户机上的训练数据通常基于特定用户对移动设备的使用，因此任何特定用户的本地数据集都不能代表总体分布。
• 不平衡：同样，一些用户会比其他用户更频繁地使用服务或应用程序，从而导致不同数量的本地训练数据。
• 大规模分布：我们预计参与优化的客户机数量将远远大于每个客户机的平均样例数量。
• 有限的沟通：移动设备经常处于离线状态，或连接速度慢或费用高。

　　在这项工作中，我们的重点是优化的非IID和不平衡特性，以及通信约束的临界性质。部署的联邦优化系统还必须解决大量的实际问题：随着数据的添加和删除而变化的客户端数据集；以复杂方式与本地数据分布相关联的客户端可用性（例如，来自美式英语使用者的电话与说英式英语使用者的电话充电有着不同的时间）；以及客户从不响应或发送损坏的更新。

　　这些问题超出了当前工作的范围；相反，我们使用一个适合实验的受控环境，但仍然需要解决客户机可用性和不平衡和非IID数据的关键问题。我们假设一个同步更新方案，该方案进行多轮通信。有一组固定的K个客户机，每个客户机都有一个固定的本地数据集。在每一轮开始时，客户机随机划分成了占比为C的若干个部分，服务器将当前全局算法状态发送给每个客户机（例如，当前模型参数）。为了提高效率，我们只选择了一个部分的客户，因为我们的实验表明，超过某一点增加更多客户的回报会减少。然后，每个选定的客户机根据全局状态及其本地数据集执行本地计算，并向服务器发送更新。然后，服务器将这些更新应用于其全局状态，并重复该过程。

　　当我们关注非凸神经网络目标时，我们考虑的算法适用于任何形式的有限和目标

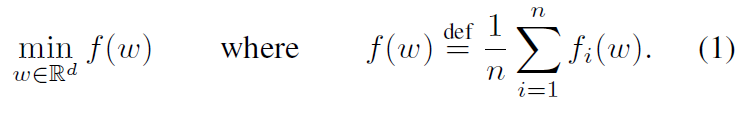
　　对于机器学习问题，我们通常采用 f_i(w) = l(x_i , y_i ; w)，即模型参数w在样例（x_i；y_i）上的预测损失。我们假设有K个客户机对数据进行划分，P_k是客户机k上的数据点的索引集，其中n_k＝|P_k|。因此，我们可以将目标（1）改写为

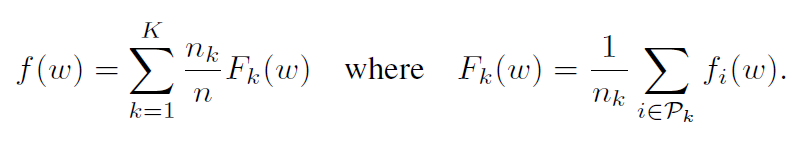
　　如果划分P_k是通过在客户机上均匀随机分布训练样例形成的，那么我们将得到 E_Pk[F_k(w)] = f(w)，其中期望值计算的是分配给固定客户机k的一组样例。这是通常由分布式优化算法所做的IID假设；我们将其他情况称为非IID设置（即F_k可能是 f 的任意错误近似值）。

　　在数据中心优化中，通信成本相对较小，计算成本占主导地位，最近的许多重点是使用GPU来降低这些成本。相反，在联邦优化中，通信成本占主导地位——我们通常会受到1 MB/s或更低的上传带宽的限制。此外，客户通常只在接入电源和使用未计量的Wi-Fi连接时自愿参与优化。此外，我们希望每个客户每天只参与少量的更新轮次。另一方面，由于与总数据集大小相比，任何单个设备上的数据集都很小，而且现代智能手机具有相对较快的处理器（包括GPU），因此对许多类型的模型来说，与通信成本相比，计算基本上是免费的。因此，我们的目标是使用额外的计算来减少训练模型所需的通信轮数。有两种主要的方法可以添加计算：1）增加并行性，在每轮通信之间使用更多独立工作的客户机；2）增加每个客户机上的计算，而不是执行像梯度计算这样的简单计算，每个客户机在每轮通信之间形成一个更复杂的计算。我们研究了这两种方法，但是我们实现的加速主要是由于一旦使用了客户机上的最小并行级别，就在每个客户机上增加了更多的计算。

 

Related Work　　局部迭代平均训练模型的分布式训练被McDonald等人[28]用于感知器，同时也被Povey等人[31]用于语音识别DNNs。Zhang等人[42]研究了具有“软”平均的异步方法。这些工作只考虑集群/数据中心的设置（最多16个工作人员，基于快速网络的挂钟时间），而没考虑不平衡和非IID的数据集。这是对联邦学习设置至关重要的属性。我们将这种类型的算法应用到联邦设置，并执行适当的实证评估。这体现出了不同于数据中心设置的问题，并且需要不同的方法。

　　与我们的动机相似，Neverova等人[29]也讨论了在设备上保留敏感用户数据的优点。Shokri和Shmatikov[35]的工作与我们有几个方面的关联：专注于训练深度网络，强调隐私的重要性，并且通过在每轮通信中只共享参数的一个子集来解决通信成本；但是，他们也没考虑不平衡的非IID数据，实证评估有限。

　　在凸设置中，分布式优化和估计问题受到了广泛关注[4，15，33]，一些算法特别关注通信效率[45，34，40，27，43]。除了假设凸性之外，现有的工作通常要求客户机的数量比每个客户机的样例数量小得多，数据以IID的方式分布在客户机上，并且每个节点都有相同数量的数据点——所有这些假设都违反了联邦优化的设置。异步分布形式的SGD也被应用于训练神经网络，例如Dean等人[12]。但是这些方法需要在联邦设置中进行大量的更新。分布式共识算法（如[41]）放宽了IID的假设，但仍然不适合在许多客户机上进行通信受限的优化。

　　我们考虑的（参数化）算法系列的一个端点是简单的单次平均，其中每个客户机都会解决模型问题，使本地数据损失最小化（可能是规则化），这些模型被平均以生成最终的全局模型。这种方法在具有IID数据的凸情况下得到了广泛的研究，并且众所周知，在最坏的情况下，生成的全局模型并不比在单个客户机上训练模型更好[44，3，46]。

 

2　　The FederatedAveraging Algorithm

　　最近许多成功的深度学习应用几乎完全依赖于变量的随机梯度下降（SGD）来进行优化；事实上，许多进展可以理解为使模型结构（以及损失函数）更易于通过简单的基于梯度的方法[16]进行优化。因此，我们很自然地从SGD开始构建联邦优化算法。

　　SGD可以简单地应用于联邦优化问题，在联邦优化问题中，每轮通信都要进行一次单批梯度计算（比如在随机选择的客户机上）。这种方法计算效率很高，但需要大量的训练来生成好的模型（例如，即使使用先进的方法，如批量标准化，Ioffe和Szegedy[21]在MNIST数据集上用大小为60的小批量上训练了50000步）。我们在CIFAR-10实验中考虑了这个基线。

　　在联邦设置中，涉及更多客户时，壁钟时间成本很低。因此对于我们的基线，我们使用大批量同步SGD；Chen等人[8]的实验显示此方法在数据中心设置中是最先进的，它优于异步方法。为了在联邦设置中应用这种方法，我们在每一轮中选择占比为C的客户机，并计算这些客户机所持有的所有数据的损失梯度。因此，C控制全局批大小，C=1对应于整批（非随机）梯度下降。我们将此基线算法称为联邦SGD（或FedSGD）。

 

 

　　(部分省略) 也就是说，每个客户端使用其本地数据在当前模型上进行一步梯度下降，然后服务器对生成的模型进行加权平均。我们称之为联邦平均算法（FedAvg）。以这种方式编写算法后，我们可以在平均步骤之前多次迭代本地更新，从而向每个客户机添加更多的计算。计算量由三个关键参数控制：C，每轮执行计算的客户端的占比；E，每个客户端在每轮对本地数据集进行训练的次数；B，用于客户端更新的本地小批量大小。我们令B = ∞来表明将完整的本地数据集视为单个小批处理。因此，在该算法家族中，我们可以取B = ∞且E = 1，这与FedSGD完全对应。对于具有n_k个本地样例的客户机，每轮本地更新的次数由u_k = E * n_k / B给出；完整的伪代码在算法1中给出。

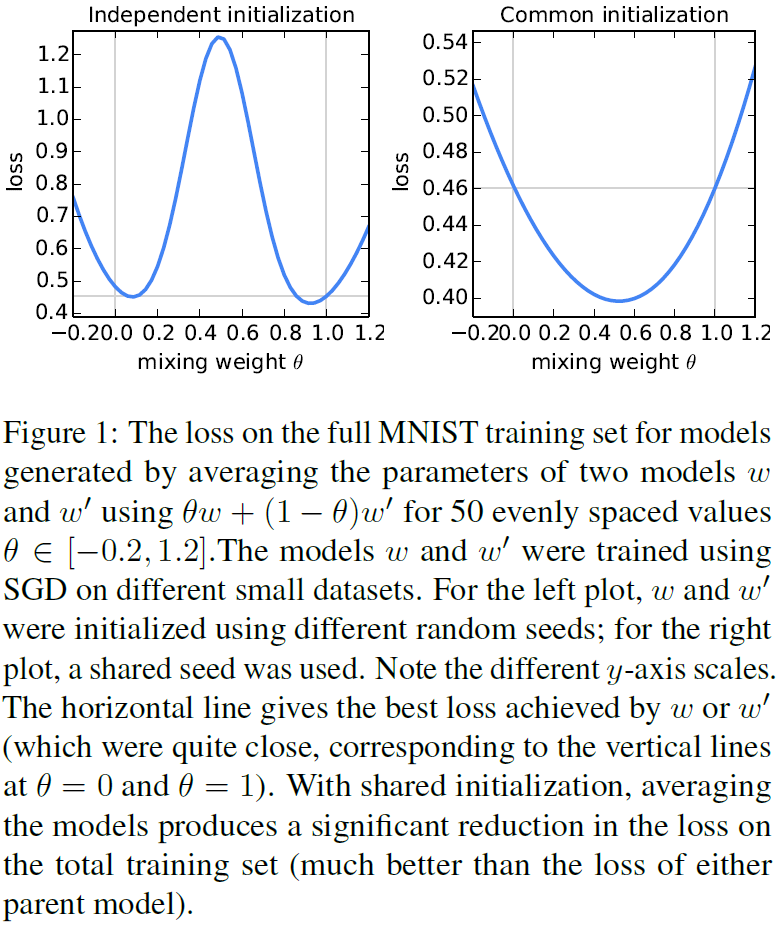
　　对于一般的非凸目标，参数空间中的平均模型会产生任意的坏模型。遵循Goodfellow等人[17]的方法，当我们将两个从不同初始条件训练的MNIST数字识别模型取平均时，我们可以看到这种不良表现（图1，左图）。对于这个图，父模型w和w’分别接受了来自MNIST训练集的600个不重叠的IID样本的训练。通过SGD进行训练，固定学习率为0.1，在大小为50的小批量上更新迭代了240次（或E=20，通过大小为600的小数据集）。这大约是模型开始过度适合其本地数据集的训练量。

　　最近的研究表明，在实践中，充分超参数化NNs的损失面表现出令人惊讶的良好，特别是比先前想象的更不容易出现不良的局部极小值[11，17，9]。事实上，当我们从相同的随机初始化开始两个模型，然后在不同的数据子集上对每个模型进行独立的训练（如上所述），我们发现简单的参数平均非常有效（图1，右）：这两个模型的平均值，w/2+w''/2，实现了对整个MNIST训练集损失的大幅降低，而不是通过单独对任何一个小数据集进行训练而获得的最佳模型。虽然图1从随机初始化开始，但是注意到对于每一轮FedAvg都使用一个共享的启动模型w_t，因此同样的直觉也适用。

 

3　　Experimental Results

　　我们受到图像分类和语言建模任务的激励，良好的模型可以大大提高移动设备的可用性。对于这些任务中的每一个，我们首先选择一个足够小的代理数据集，这样我们就可以彻底研究FedAvg算法的超参数。虽然每个单独的训练运行相对较小，但我们为这些实验训练了2000多个单独的模型。然后，我们在基准CIFAR-10图像分类任务上给出了结果。最后，为了证明FedAvg在采用客户机自然划分数据的实际问题上的有效性，我们对一个大型语言建模任务进行了评估。

　　我们的初步研究包括两个数据集上的三个模型族。前两个用于MNIST数字识别任务[26]：1）一个简单的多层感知器，具有两个隐层，每个层有200个单元，使用ReLu激活（共199210个参数），我们称之为MNIST 2NN。2）具有两个5x5卷积层的CNN（第一个具有32个通道，第二个具有64个通道，每个通道后面都有2x2最大池），一个具有512个单元和ReLu激活的全连接层，以及一个最终的softmax输出层（总参数1663370）。为了研究联邦优化，我们还需要指定数据如何分布在客户机上。我们研究了在客户机上对MNIST数据进行划分的两种方法：IID，在IID中对数据进行洗牌，然后将数据分为100个客户机，每个客户机接收600个样例；而非IID，我们首先按数字标签对数据进行排序，将其分为200个大小为300的碎片，然后将这些碎片分配给100个客户机，每个客户机2个碎片。这是一个病理性的非IID数据分区，因为大多数客户只有两位数的样例。因此，这让我们可以探索我们的算法在高度非IID数据上的突破程度。然而，这两个划分都是平衡的。

　　为了进行语言建模，我们从威廉·莎士比亚的完整作品中构建了一个数据集[32]。我们用至少两行文本为剧本中每个有对话的角色构建了一个客户端数据集。这产生了一个拥有1146个客户机的数据集。对于每个客户机，我们将数据分成一组训练行（角色的前80%行）和测试行（最后20%，四舍五入到至少一行）。生成的数据集在训练集中有3564579个字符，在测试集中有870014个字符。这些数据基本上是不平衡的，许多角色只有几行，而少数角色有大量行。此外，观察测试集不是随机的线条样本，而是由每个剧本的时间顺序暂时分开的。使用相同的训练/测试拆分，我们还可以形成平衡和IID版本的数据集，同时拥有1146个客户机。

　　在这些数据上，我们训练了一个堆叠的字符级LSTM语言模型[22]，该模型在读取一行中的每个字符后，预测下一个字符。该模型以一系列字符作为输入，并将每个字符嵌入到一个已知的8维空间中。然后通过两个LSTM层处理嵌入的字符，每个层有256个节点。最后，将第二个LSTM层的输出发送到softmax输出层，每个字符一个节点。整个模型有866578个参数，我们使用80个字符的展开长度进行训练。

　　SGD对学习速率参数η的调整很敏感。这里报告的结果是基于一个足够宽的学习率网格上的训练（通常给η取11-13个值，在一个乘法分辨率10^1/3或10^1/6网格上）。我们检查以确保最佳学习率在网格中间，并且最佳学习率之间没有显著差异。除非另有说明，我们为每个x轴值分别选择的最佳执行率绘制度量。我们发现，最佳学习率与其他参数之间的关联不大，不存在明显的函数关系。

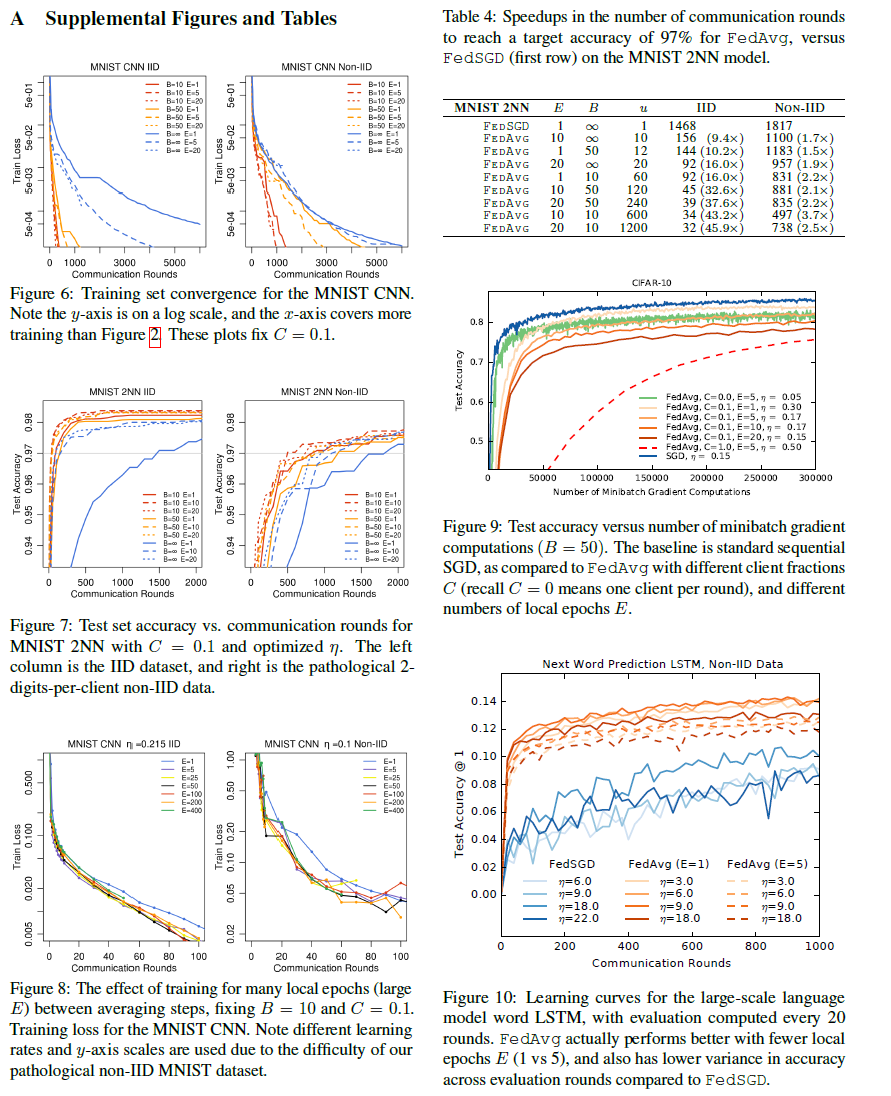
Increasing parallelism　　我们首先对客户端占比C进行实验，它控制多客户端并行的数量。表1显示了不同的C对两个MNIST模型的影响。我们报告了实现目标测试集精度所需的通信轮数。为了计算这一点，我们为每个参数设置组合构建了一条学习曲线，如前所述对η进行优化，然后利用在所有先前轮次中获得的测试集精度的最佳值，对每条曲线加以改进。然后，我们使用组成曲线的离散点之间的线性插值，计算曲线与目标精度交汇处的轮数。参考图2可以更好地理解这一点，其中灰色线表示目标。

 

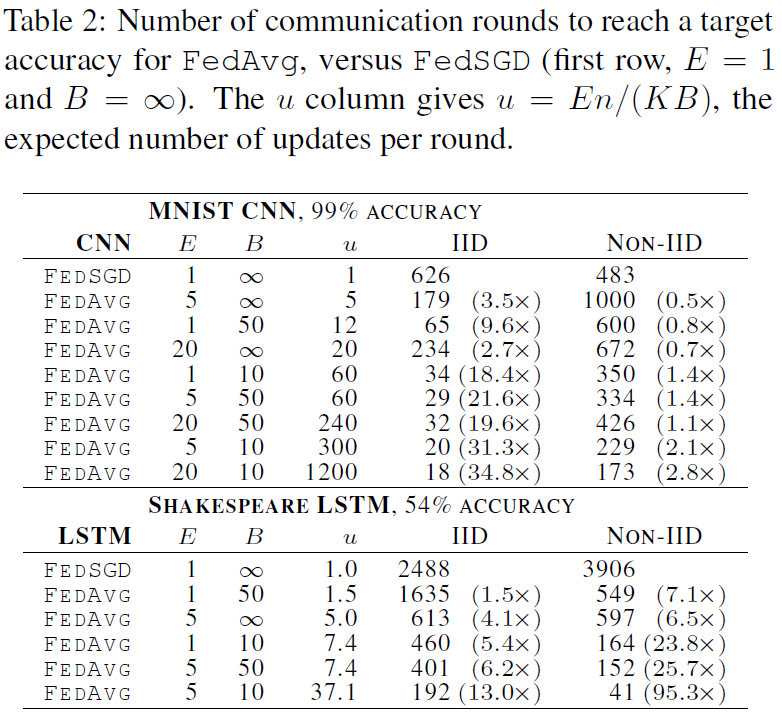
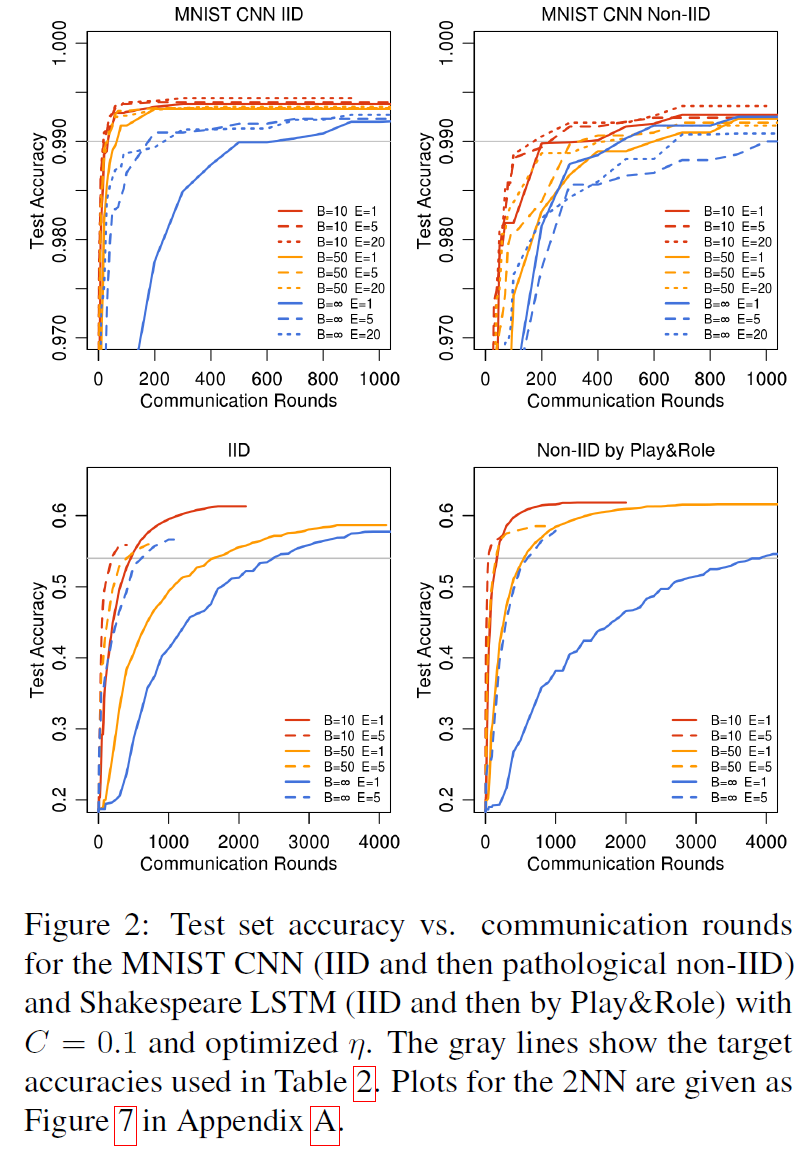
　　当B=∞时（对于MNIST，将所有600个客户机样例处理作为每轮的一批），增加客户机占比的优势很小。当使用C≥0.1时，特别是在非IID情况下，更小的批处理大小B=10显示出显著的改进。基于这些结果，在我们剩下的大部分实验中，我们将C=0.1固定下来，这在计算效率和收敛速度之间达到了很好的平衡。将表1中B=∞和B=10列的轮数进行比较，可以看到一个急剧性的加速，我们接下来将对此进行研究。

 

Increasing computation per client　　在本节中，我们将C=0.1固定下来，并在每一轮中为每个客户机添加更多的计算，要么减少B，要么增加E，要么两者兼而有之。图2表明，每轮增加更多的本地SGD更新可以显著降低通信成本，表2量化了这些加速。每轮每个客户机的预期更新数为u = (E[n_k] / B)E = nE / (KB) ，其中预期值超过随机客户机k的绘制值。我们通过此统计对表2的每个部分中的行进行排序。我们看到通过改变E和B来增加u是有效的。只要B足够大，可以充分利用客户机硬件上可用的并行性，就基本上不需要花费计算时间来降低它，因此在实践中，这应该是第一个被调优的参数。

　　对于MNIST数据的IID划分，每个客户使用更多的计算，减少了达到目标精度的轮数，其中CNN减少了35倍，2NN减少了46倍（有关2NN的详细信息，请参见附录A中的表4）。病理性划分非IID数据的加速率更小，但仍相当可观（2.8–3.7倍）。令人印象深刻的是，对训练不同数字对的模型参数，当我们幼稚地进行平均时，平均值提供了所有的优势（而实际上是分散的）。因此，我们认为这是该方法鲁棒性的有力证据。

　　莎士比亚（根据戏剧中的角色）的不平衡和非IID分布更能代表我们对现实应用所期望的那种数据分布。令人欣慰的是，对于这个问题，学习非IID和不平衡数据实际上要容易得多（95倍加速，而平衡IID数据为13倍加速）；我们推测这主要是由于某些角色具有相对较大的本地数据集，这使得增加的本地训练尤其有价值。

　　对于所有的三个模型类，FedAvg比基线FedSGD模型收敛到更高的测试集精度水平。即使这些线超出了绘制的范围，这种趋势也会继续。例如，对于CNN来说，B=∞；E=1 FedSGD模型在1200轮之后最终达到99.22%的精度（6000轮之后没有进一步提高），而B=10；E=20 FedAvg模型在300轮之后达到99.44%的精度。我们推测，除了降低通信成本外，模型平均还能产生类似于Dropout[36]所获得的正则化收益。

　　我们主要关注的是泛化性能，但是FedAvg在优化训练损失方面也很有效，甚至超过了测试集精度的最大值。我们观察了所有三个模型类的类似行为，并在附录A的图6中展示了MNIST CNN的图。

 

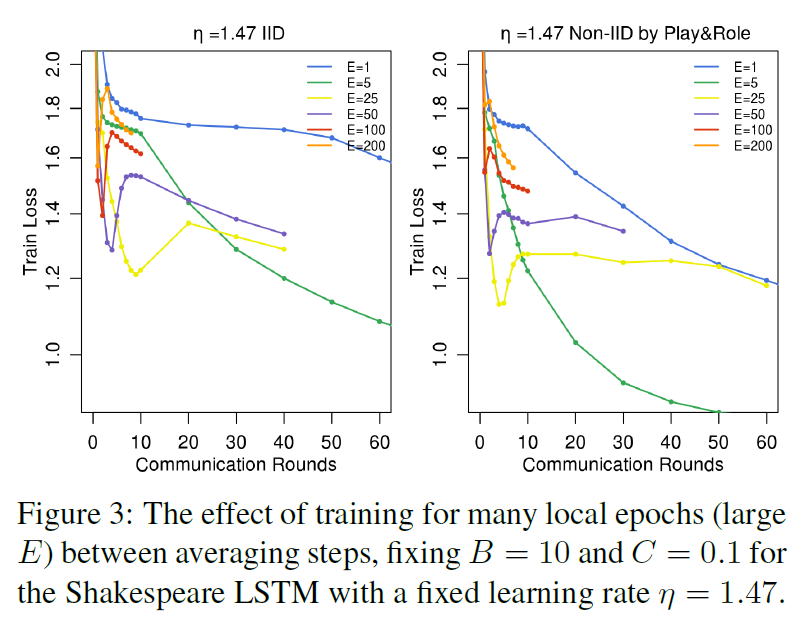
Can we over-optimize on the client datasets?　　当前模型参数只影响通过初始化在每个ClientUpdate中执行的优化。因此，当E 一> ∞，至少对于凸问题，最终初始条件应该是无关的，并且无论初始化如何，都会达到全局最小值。即使对于非凸问题，也可以推测，只要初始化在同一个盆地中，算法就会收敛到相同的局部极小值。也就是说，我们希望，虽然一轮平均可能会产生一个合理的模型，但额外的一轮交流（和平均）不会产生进一步的改进。

　　图3显示了初始训练选择大的E值对莎士比亚LSTM问题的影响。事实上，对于非常大的本地epoch（1个epoch等于使用训练集中的全部样本训练一次），FedAvg可以是平稳的，也可以是发散的。这一结果表明，对于某些模型，特别是在收敛的后期阶段，用衰减学习率的方法衰减每轮的局部计算量（移动到更小的E或更大的B）可能是有用的。附录A中的图8给出了MNIST CNN的类似实验。有趣的是，对于这个模型，我们看不到大数值的E对收敛速度的显著下降。但是，对下面描述的大规模语言建模任务（参见附录A中的图10），我们看到E=1的性能略好于E=5。

CIFAR experiments　　我们还对CIFAR-10数据集[24]进行了实验，以进一步验证FedAvg。数据集由10类32x32的RGB图像组成。我们将50000个训练样例和10000个测试样例分成100个客户机，每个客户机包含500个训练样例和100个测试样例；由于此数据没有自然的用户划分，因此我们考虑了平衡和IID设置。模型架构取自TensorFlow教程[38]，该模型由两个卷积层、两个全连接的层和一个线性转换层组成，以生成总共约10⁶个参数的逻辑。请注意，最先进的方法已经达到了CIFAR的96.5%[19]的测试精度；然而，我们使用的标准模型足以满足我们的需要，因为我们的目标是评估我们的优化方法，而不是在这项任务上实现可能的最佳精度。图像作为训练输入管道的一部分进行预处理，包括将图像裁剪为24x24，随机左右翻转，调整对比度、亮度和白化。

 

　　对于这些实验，我们考虑了一个额外的基线，即全训练集（无用户划分）上的标准SGD训练，使用大小为100的小批量。在197500个小批量更新之后，我们获得了86%的测试精度（每个小批量更新都需要在联邦设置中进行通信）。FedAvg仅在2000次通信轮次后达到了85%的类似测试精度。对于所有算法，除了初始学习速率外，我们还调整了学习速率衰减参数。表3给出了基线SGD、FedSGD和FedAvg达到三个不同精度目标的通信次数，图4给出了FedAvg与FedSGD的学习率曲线。

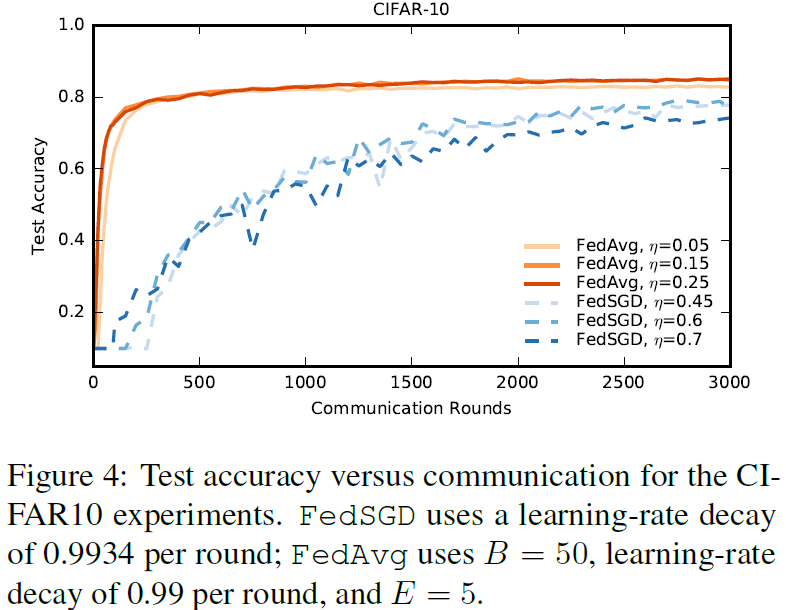
　　通过对SGD和FedAvg运行B=50的小批量实验，我们还可以将精度视为此类小批量梯度计算数量的函数。我们期望SGD在这里做得更好，因为在每一个小批量计算之后都会有一个连续的步骤。然而，如附录中的图9所示，对于C和E的适度值，FedAvg在每一个小批量计算中都有类似的进展。此外，我们发现每轮只有一个客户机的标准SGD和FedAvg（C=0）在精度上表现出显著的振荡，而对更多客户机的平均则可以消除这种振荡。

 

 

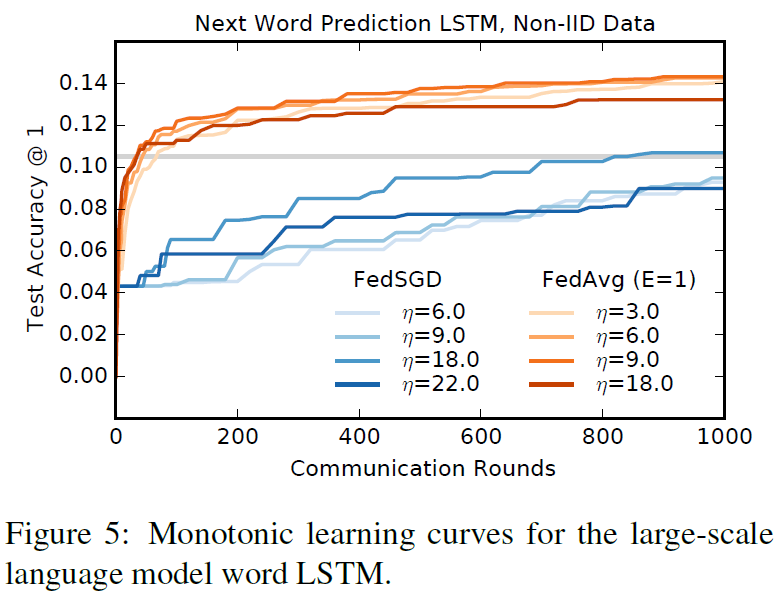
Large-scale LSTM experiments　　我们对一个大规模的下一个单词预测任务进行了实验，以证明我们的方法在现实问题上的有效性。我们的训练数据集包括来自大型社交网络的1000万个公共邮件。我们按作者对这些邮件进行分组，总共有50多万个客户。此数据集是用户移动设备上存在的文本输入数据类型的现实代理。我们将每个客户数据集限制在最多5000个字，并在来自不同（非训练）作者的1e5邮件测试集上报告准确性（在10000个可能性中，预测概率最高的数据部分在正确的下一个词上）。我们的模型是一个256节点的LSTM，词汇表上有10000个单词。每个字的输入和输出嵌入尺寸为192，并与模型共同训练，共有4950544个参数。我们用了10个单词展开。

　　这些实验需要大量的计算资源，因此我们没有彻底地探索超参数：所有的实验都在每轮200个客户机上进行；FedAvg使用B=8和E=1。我们研究了FedAvg和基线FedSGD的各种学习率。图5显示了最佳学习率的单调学习曲线。η=18.0的FedSGD需要820轮才能达到10.5%的精度，而η=9.0的FedAvg仅在35个通信轮次中达到10.5%的精度（比FedSGD少23倍）。我们观察到FedAvg的测试精度差异较低，见附录A中的图10。该图还包括E=5的结果，该结果比E=1稍差。

 

4 Conclusions and Future Work

　　我们的实验表明，联邦学习是可行的，因为FedAvg使用相对较少的通信轮次来训练高质量的模型，正如在各种模型结构上的结果所证明的那样：一个多层感知器，两个不同的卷积NNs，一个两层字符LSTM和大规模的字级LSTM。             

　　虽然联邦学习提供了许多实际的隐私好处，但通过差异隐私[14、13、1]提供更强大的保证，安全的多方计算[18]或它们的组合是未来工作的一个有趣方向。请注意，这两类技术最自然地应用于同步算法，如FedAvg。

 

References

[1] Martin Abadi, Andy Chu, Ian Goodfellow, Brendan McMahan, Ilya Mironov, Kunal Talwar, and Li Zhang. Deep learning with differential privacy. In 23rd ACM Conference on Computer and Communications Security (ACM CCS), 2016.
[2] Monica Anderson. Technology device ownership: 2015. http://www.pewinternet.org/2015/10/29/technology-device-ownership-2015/, 2015.
[3] Yossi Arjevani and Ohad Shamir. Communication complexity of distributed convex learning and optimization. In Advances in Neural Information Processing Systems 28. 2015.
[4] Maria-Florina Balcan, Avrim Blum, Shai Fine, and Yishay Mansour. Distributed learning, communication complexity and privacy. arXiv preprint arXiv:1204.3514, 2012.
[5] Yoshua Bengio, R´ejean Ducharme, Pascal Vincent, and Christian Janvin. A neural probabilistic language model. J. Mach. Learn. Res., 2003.
[6] Keith Bonawitz, Vladimir Ivanov, Ben Kreuter, Antonio Marcedone, H. Brendan McMahan, Sarvar Patel, Daniel Ramage, Aaron Segal, and Karn Seth. Practical secure aggregation for federated learning on user-held data. In NIPS Workshop on Private Multi-Party Machine Learning, 2016.
[7] David L. Chaum. Untraceable electronic mail, return addresses, and digital pseudonyms. Commun. ACM, 24(2), 1981.
[8] Jianmin Chen, Rajat Monga, Samy Bengio, and Rafal Jozefowicz. Revisiting distributed synchronous sgd. In ICLR Workshop Track, 2016.
[9] Anna Choromanska, Mikael Henaff, Micha¨el Mathieu, G´erard Ben Arous, and Yann LeCun. The loss surfaces of multilayer networks. In AISTATS, 2015.
[10] Greg Corrado. Computer, respond to this email. http://googleresearch.blogspot.com/2015/11/computer-respond-to-this-email.html, November 2015.
[11] Yann N. Dauphin, Razvan Pascanu, C¸ aglar G¨ulc¸ehre, KyungHyun Cho, Surya Ganguli, and Yoshua Bengio. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In NIPS, 2014.
[12] Jeffrey Dean, Greg S. Corrado, Rajat Monga, Kai Chen, Matthieu Devin, Quoc V. Le, Mark Z. Mao, Marc’Aurelio Ranzato, Andrew Senior, Paul Tucker, Ke Yang, and Andrew Y. Ng. Large scale distributed deep networks. In NIPS, 2012.
[13] John Duchi, Michael I. Jordan, and Martin J. Wainwright. Privacy aware learning. Journal of the Association for Computing Machinery, 2014.
[14] Cynthia Dwork and Aaron Roth. The Algorithmic Foundations of Differential Privacy. Foundations and Trends in Theoretical Computer Science. Now Publishers, 2014.
[15] Olivier Fercoq, Zheng Qu, Peter Richt´arik, and Martin Tak´ac. Fast distributed coordinate descent for nonstrongly convex losses. In Machine Learning for Signal Processing (MLSP), 2014 IEEE International Workshop on, 2014.
[16] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. Book in preparation for MIT Press, 2016.
[17] Ian J. Goodfellow, Oriol Vinyals, and Andrew M. Saxe. Qualitatively characterizing neural network optimization problems. In ICLR, 2015.
[18] Slawomir Goryczka, Li Xiong, and Vaidy Sunderam. Secure multiparty aggregation with differential privacy: A comparative study. In Proceedings of the Joint EDBT/ICDT 2013 Workshops, 2013.
[19] Benjamin Graham. Fractional max-pooling. CoRR, abs/1412.6071, 2014. URL http://arxiv.org/abs/1412.6071.
[20] Sepp Hochreiter and J¨urgen Schmidhuber. Long shortterm memory. Neural Computation, 9(8), November 1997.
[21] Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015.
[22] Yoon Kim, Yacine Jernite, David Sontag, and Alexander M. Rush. Character-aware neural language models. CoRR, abs/1508.06615, 2015.
[23] Jakub Koneˇcn´y, H. Brendan McMahan, Felix X. Yu, Peter Richtarik, Ananda Theertha Suresh, and Dave Bacon. Federated learning: Strategies for improving communication efficiency. In NIPS Workshop on Private Multi-Party Machine Learning, 2016.
[24] Alex Krizhevsky. Learning multiple layers of features from tiny images. Technical report, 2009.
[25] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS. 2012.
[26] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 1998.
[27] Chenxin Ma, Virginia Smith, Martin Jaggi, Michael I Jordan, Peter Richt´arik, and Martin Tak´aˇc. Adding vs. averaging in distributed primal-dual optimization. In ICML, 2015.
[28] Ryan McDonald, Keith Hall, and Gideon Mann. Distributed training strategies for the structured perceptron. In NAACL HLT, 2010.
[29] Natalia Neverova, Christian Wolf, Griffin Lacey, Lex Fridman, Deepak Chandra, Brandon Barbello, and Graham W. Taylor. Learning human identity from motion patterns. IEEE Access, 4:1810–1820, 2016.
[30] Jacob Poushter. Smartphone ownership and internet usage continues to climb in emerging economies. Pew Research Center Report, 2016.
[31] Daniel Povey, Xiaohui Zhang, and Sanjeev Khudanpur. Parallel training of deep neural networks with natural gradient and parameter averaging. In ICLR Workshop Track, 2015.
[32] William Shakespeare. The Complete Works of William Shakespeare. Publically available at https://www.gutenberg.org/ebooks/100.
[33] Ohad Shamir and Nathan Srebro. Distributed stochastic optimization and learning. In Communication, Control, and Computing (Allerton), 2014.
[34] Ohad Shamir, Nathan Srebro, and Tong Zhang. Communication efficient distributed optimization using an approximate newton-type method. arXiv preprint arXiv:1312.7853, 2013.
[35] Reza Shokri and Vitaly Shmatikov. Privacy-preserving deep learning. In Proceedings of the 22Nd ACM SIGSAC Conference on Computer and Communications Security, CCS ’15, 2015.
[36] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. 15, 2014.
[37] Latanya Sweeney. Simple demographics often identify people uniquely. 2000.
[38] TensorFlow team. Tensorflow convolutional neural networks tutorial, 2016. http://www.tensorflow.org/tutorials/deep_cnn.
[39] White House Report. Consumer data privacy in a networked world: A framework for protecting privacy and promoting innovation in the global digital economy. Journal of Privacy and Confidentiality, 2013.
[40] Tianbao Yang. Trading computation for communication: Distributed stochastic dual coordinate ascent. In Advances in Neural Information Processing Systems, 2013.
[41] Ruiliang Zhang and James Kwok. Asynchronous distributed admm for consensus optimization. In ICML. JMLR Workshop and Conference Proceedings, 2014.
[42] Sixin Zhang, Anna E Choromanska, and Yann LeCun. Deep learning with elastic averaging sgd. In NIPS. 2015.
[43] Yuchen Zhang and Lin Xiao. Communication-efficient distributed optimization of self-concordant empirical loss. arXiv preprint arXiv:1501.00263, 2015.
[44] Yuchen Zhang, Martin J Wainwright, and John C Duchi. Communication-efficient algorithms for statistical optimization. In NIPS, 2012.
[45] Yuchen Zhang, John Duchi, Michael I Jordan, and Martin J Wainwright. Information-theoretic lower bounds for distributed statistical estimation with communication constraints. In Advances in Neural Information Processing Systems, 2013.
[46] Martin Zinkevich, Markus Weimer, Lihong Li, and Alex J. Smola. Parallelized stochastic gradient descent. In NIPS. 2010.

 

 

 

COMPRESSING DEEP CONVOLUTIONAL NETWORKS USING VECTOR QUANTIZATION 论文笔记

• 摘要

深度卷积神经网络（CNN）已成为最有前途的物体识别方法，近年来反复展示了图像分类和物体检测的破纪录结果。然而，非常深的CNN通常涉及具有数百万个参数的许多层，使得网络模型的存储非常大。这限制在资源有限的硬件上使用深度CNN，尤其是手机或其他嵌入式设备。在本文中，我们通过研究用于压缩CNN参数的信息理论矢量量化方法来解决该模型存储问题。特别地，我们已经发现在压缩大多数存储要求密集的连接层方面，矢量量化方法比现有的矩阵分解方法具有明显的增益。简单地将k均值聚类应用于权重或进行product量化可以在模型大小和识别准确度之间实现非常好的平衡。对于ImageNet挑战中的1000类别分类任务，我们能够使用最先进的CNN实现16-24倍的网络压缩，只有1％的分类精度损失。

• 压缩紧密的连接层

在本节中，我们考虑两类压缩密集连接层中的参数的方法。 我们首先考虑矩阵分解方法，然后介绍矢量量化方法。

• 矩阵分解法

我们首先考虑矩阵分解方法，这些方法已被广泛用于加速CNN（Denton等，2014）以及压缩线性模型中的参数（Denton等，2014）。 特别地，我们考虑使用奇异值分解（SVD）来分解参数矩阵。 给定一个密集连通层中的参数W ，我们将其分解为(公式见论文）

为了使用两个小得多的矩阵近似W，我们可以在U和V中选择具有相应特征值的前k个奇异向量，以重建W：（公式见论文）

SVD的近似由沿着S中的特征值的衰减控制.SVD方法在Frobenius范数的意义上是最优的，其最小化了近似矩阵和原始W之间的MSE误差。两个低秩矩阵U''和V''以及特征值必须存储。 因此，给定m，n和k的压缩率计算为mn = k（m + n + 1）。

•  向量量化法

　　1.二值化

　　我们从量化参数矩阵的最简单方法开始。 给定参数W，我们采用矩阵的符号作为量化结果。

　　这种方法主要受到Dropconnect（Wan et al。，2013）的启发，它在训练期间将部分参数（神经元）随机设置为0。 在这里，我们采取更积极的方法，如果它是正的，则打开每个神经元，当它是负的时将其关闭。 从几何角度来看，假设密集连接层是一组超平面，我们实际上是将每个超平面四舍五入到最近的坐标。 该方法将数据压缩32倍，因为每个神经元由一位表示。

　　2.使用k-means进行标量量化

　　另一种简单的方法是对参数执行标量量化。 对于W，我们可以将其所有标量值收集为w，并对值进行k-means聚类（公式见论文）

　　其中w和c都是标量。 在聚类之后，w中的每个值被分配一个聚类索引，并且可以由聚类中心的c形成码本。 在预测期间，我们可以直接在c中查找每个wij的值。 因此，重建矩阵是：（公式见论文）

　　对于这种方法，我们只需要将索引和码本存储为参数。 给定k个中心，我们只需要log2（k）位来编码中心。 例如，如果我们使用k = 256个中心，则每个簇索引只需要8位。 因此，压缩率是32 = log2（k），假设我们使用原始W的浮点数并假设码本本身可以忽略不计。 尽管这种方法很简单，但我们的实验表明，这种方法在压缩参数方面具有令人惊讶的良好性能

　　3.Product 量化

　　接下来，我们考虑用于压缩参数的结构化矢量量化方法。 特别是，我们考虑使用product量化（PQ）（Jegou等，2011），它探讨了向量空间中结构的冗余。 PQ的基本思想是将向量空间划分为许多不相交的子空间，并在每个子空间中执行量化。 由于假设每个子空间中的向量都是冗余的并且通过在每个子空间中执行量化，我们能够更好地探索冗余结构。 具体来说，给定矩阵W，我们将它逐列分成几个子矩阵：（公式见论文）

　　注意，PQ可以应用于矩阵的x轴或y轴。 在我们的实验中，我们评估了两种情况。

　　对于这种方法，我们需要为每个子向量存储索引和码本。 特别是，与标量量化情况相反，这里的码本不可忽略。

　　4.Residual 量化

　　我们考虑的第三种量化方法是残差量化（Chen et al。，2010），它是结构化量化的另一种形式。 基本思想是首先将矢量量化为k个中心，然后递归地量化残差。 例如，给定一组向量wi，在第一阶段，我们首先使用k-means聚类将它们量化为k个不同的向量：（公式见论文）

　　每个向量wz将由其最近的中心c1j表示。 接下来，我们计算所有数据点的wz和c1j之间的残差r1z，并将残差矢量r1z递归地量化为k个不同的码字c2j。 最后，可以通过在每个阶段添加相应的中心来重建矢量：（公式见论文）

　　5.其他方法和讨论

　　上述（KM，PQ和RQ）是用于压缩矩阵的三种不同类型的矢量量化方法。 KM仅捕获每个神经元的冗余（单个标量）; PQ探索了一些局部冗余结构; 并且RQ试图探索权重向量之间的全局冗余结构。 研究学习参数的行为中存在哪种冗余将是有趣的。

　　许多基于学习的二值化或product量化方法是可用的，例如Spectral Hashing（Weiss等人，2008），Iterative Quantization（Gong等人，2012）和Catesian kmeans（Norouzi＆Fleet，2013）等。 然而，它们不适合于该特定任务，因为我们需要存储非常大的学习参数矩阵（例如，旋转矩阵）。 因此，我们不考虑本文中的其他方法。 在执行PQ时探索W中的结构也很有趣。 特别是，因为在不同滤波器的一组输出上学习W，所以将来自特定滤波器的输出分组在一起或将来自不同滤波器的特定维度分组在一起可能是有趣的。 然而，在我们的初步调查中，我们在进行PQ时通过探索这种结构没有发现任何改善。 因此，我们按默认顺序对这些维度进行分组。

• 实验
• 实验设置

　　我们在ILSVRC2012基准图像分类数据集上评估了这些不同的方法。 该数据集包含来自1000个对象类别的100多万个训练图像。 它还具有20,000个图像的验证集，每个类别包含20个图像。 我们对标准训练集进行了训练，对参数进行了压缩，并在验证集上进行了测试。

　　我们使用的卷积神经网络，来自Zeiler＆Fergus（2013），包含5个卷积层和3个密集连接层。 首先将所有输入图像调整为最小尺寸257，之后我们对进行随机裁剪到分辨率为225X225。 然后将图像馈送到5个不同的卷积层中，各自的滤波器尺寸为7,5,3,3和3.前两个卷积层之后是局部响应归一化层和最大池化层。 此时我们已经获得了三个完全连接的尺寸为9216X2048,2048X2048和2048X1000的层。我们在这里使用的非线性函数是RELU。 在70个epochs之后，网络在1个GPU上训练了大约5天。 学习率从0.02开始，每5-10个epochs减半; 重量衰减设定为0.0005;动量设定为0.9。

　　为了评估不同的方法，我们使用验证集上的分类准确度作为评估协议。 我们使用精度@ 1和精度@ 5来评估不同的参数压缩方法。 目标是在相同的压缩率下得到更高的精度或相同的精度实现更高的压缩率。

• Product 量化分析

　　我们首先对基于PQ的参数压缩进行了分析，因为PQ有几个不同的参数。 我们使用了不同数量的簇k = 4;8; 16（对应于2; 3; 4位）。 对于每个固定的k，我们显示不同段尺寸（列）尺寸s = 1;2;3; 4的结果，它将压缩率从低变为高。 如3.2.3节所述，我们能够对x轴或y轴执行PQ，因此显示两种情况的结果。 我们将在对齐分段大小时比较不同的PQ方法，并将它们与对齐的压缩率进行比较。

　　对于不同的轴对准，图1和图2（图见论文）中报告了精度@ 1的结果。 从图1中的结果可以看出，通过使用更多的中心k和更小的段大小s，我们能够获得更小的分类误差。 例如，在图1中，红色曲线的分类错误总是比其他方法小得多。 该结果与先前对PQ的观察结果一致（即，在每个片段中使用更多中心通常可以获得较低的量化误差率）。 但是，当我们考虑码本的大小并测量相同压缩率的准确度时，如图2所示，我们发现使用更多的中心并不总是有帮助的

　　因为他们会积极地增加码本的大小。 例如，当我们使用k = 16个中心时，分类误差显然不低于我们使用较少数量的聚类时（例如k = 8）。 这种差异是因为码本本身使用了太多的存储空间，并且压缩率非常低。 当我们比较压缩x轴和y轴的结果时，x轴的结果略好一些。 这种改进可能是因为x轴有更多的尺寸，这使得码本尺寸更大，从而减少了信息的损失。 在下一组实验中，我们将中心数量固定为8（每段3位），因为这种方法在压缩率和准确度之间实现了良好的平衡。

• 整体比较

　　下面的图3包含了我们在此介绍的所有量化方法的比较。 与上面的部分类似，我们提出了与压缩率有关的分类错误。 对于没有要调谐的参数的二进制量化，压缩率为32.对于PQ，我们每段使用8个中心并改变每个段的维度（从1到4）以实现不同的压缩率。 对于kmeans（KM），我们将簇的数量从1改为32以实现32和1之间的压缩率。对于SVD，我们改变输出维度以实现不同的压缩率。 RQ的表现不尽如人意; 在这里，我们仅报告256个中心的结果，其中t = 2; 3次迭代。 我们还尝试使用较少数量的RQ中心，但发现性能更差。

　　精度@ 1和精度@ 5都显示在图3中，我们看到这两个数字的趋势是一致的。 特别是，SVD在压缩和加速卷积层方面取得了令人瞩目的成果（Denton等，2014），但在压缩密集连接层方面效果不佳。 这种差异主要是因为仍然需要为SVD存储两个分解矩阵，

　　这不是为节省存储而优化的。 有些令人惊讶的是，kmeans虽然简单，但却能很好地完成这项任务。 我们能够使用KM实现4-8倍的压缩率，同时保持精度损失在1％以内。 应用PQ等结构化量化方法可以进一步提高KM的结果以外的性能。 对于RQ，我们发现它无法实现非常高的压缩率，主要是因为码本大小太大。 给定相同的压缩率，其准确性也比其他方法差得多。 最后，最简单的二值化方法运行得相当好。 我们无法改变其压缩率，但考虑到相同的压缩率，其性能可与KM或PQ相媲美。 此外，它的存储非常简单。 因此，当目标是非常极度地压缩数据时，这种方法也是一个不错的选择。

　　KM，PQ和RQ之间的比较提出了一些有趣的见解。 首先，KM工作得相当好，可以在不牺牲性能的情况下实现下降压缩率。 这些结果表明每个神经元之间存在相当大的冗余。 应用PQ工作得更好，这意味着在这些权重矩阵中存在非常有意义的子向量局部结构。 RQ对于这样的任务非常糟糕，这可能意味着这些权重向量中的全局结构很少。

• 单层误差分析

　　我们还对压缩每个单层的分类错误率进行了额外的分析，同时将其他层固定为未压缩。 结果报告在图4中（仅适用于精度@ 1）。 我们发现压缩第八层和第九层隐藏层通常不会导致性能显着下降，但压缩第十层和最终分类层会导致精度下降得多。 将所有三个层压缩在一起通常会导致更大的误差，尤其是当压缩率很高时。 最后，一些样本预测结果如图5所示。

• 应用于图像检索

　　本节介绍了压缩CNN在图像检索中的应用，以验证压缩网络的泛化能力。 在实际的工业应用中，许多情况下不允许将照片上传到服务器，或者将大量照片上传到服务器是不可承受的。 实际上，由于带宽限制，我们只能将一些处理过的数据（例如，图像的特征或散列）上传到服务器。 鉴于上面压缩的CNN，我们能够在手机端使用压缩的CNN处理图像，并通过仅上载处理的特征在数据库侧执行检索。

　　我们在Holidays数据集上进行了实验（Jegou等，2008）。 这是一个广泛使用的标准基准数据集，用于图像检索，包含500个不同实例的1491个图像; 每个实例包含2-3个图像。 查询图像的数量固定为500; 其余用于填充数据库。 我们使用平均精度（mAP）来评估不同的方法。 我们使用每个压缩的CNN模型从最后一个隐藏层生成2048维激活特征，并将它们用作图像检索的特征。 我们使用余弦距离来测量图像特征之间的相似性。

　　根据表1的结果，不同方法的趋势与分类结果相似; 即，PQ始终比其他方法更好地工作。 一个令人惊讶的发现是，具有2个中心（1位）的kmeans给出了高结果 - 甚至高于原始特征（我们还验证了方差为0.1％）。 然而，这是一个特殊情况，可能是因为应用程序是接近重复的图像检索，并且因为将值量化为二进制对于小图像变换更加稳健。 然而，因为我们的目标是最好地重建原始权重矩阵，这种二元kmeans案例的改进确实表明它不是一个非常准确的近似。 我们在这里没有报告RQ的结果，因为它的性能非常差。

　　总之，我们发现矢量量化CNN可以安全地应用于图像分类以外的问题。

• 讨论

　　我们已经解决了在嵌入式系统中应用矢量量化来压缩深度卷积神经网络的存储问题。 我们的工作系统地研究了如何压缩深度卷积神经网络的10^8个参数，以节省模型的存储。 与之前考虑使用矩阵分解方法的方法不同，我们提出研究一系列用于压缩参数的矢量量化方法。 我们发现通过简单地使用kmeans对参数值进行标量量化，我们能够获得8-16的参数压缩率，而不会超过0.5％top5精度损失。 此外，通过使用结构化量化方法，我们能够将参数进一步压缩多达24倍，同时将前五精度的损失保持在1％以内。

　　通过压缩参数超过20倍，我们解决了在嵌入式设备中应用最先进的CNN的问题。 鉴于具有大约200MB参数的最先进模型，我们能够将它们减少到不到10MB，这使我们能够轻松部署这些模型。 本文的另一个有趣的含义是我们的实证结果证实了Denil等人的研究结果（2013）即CNN中的有用参数约为5％（我们能够将它们压缩约20倍）。

　　将来，在嵌入式设备上探索压缩模型的硬件高效操作以加速计算将是有趣的。 将微调应用于压缩层以提高性能也很有趣。 虽然本文主要关注压缩密集连接层，但研究是否可以应用相同的矢量量化方法来压缩卷积层将是有趣的。

 

关于Depth Map Prediction from a Single Image using a Multi-Scale Deep Network的介绍已经告一段落，感谢您的耐心阅读，如果想了解更多关于AlexNet: ImageNet Classification with Deep Convolutional Neural Networks、AlexNet论文翻译-ImageNet Classification with Deep Convolutional Neural Networks、Communication-Efficient Learning of Deep Networks from Decentralized Data、COMPRESSING DEEP CONVOLUTIONAL NETWORKS USING VECTOR QUANTIZATION 论文笔记的相关信息，请在本站寻找。

本文标签：

• 深度图预测
• 单张图像
• 多尺度深度网络
• 深度学习技术