本文将带您了解关于EducationalCodeforcesRound40C.MatrixWalk(思维)的新内容,同时我们还将为您解释思维map的相关知识,另外,我们还将为您提供关于CF-Educa
本文将带您了解关于Educational Codeforces Round 40 C. Matrix Walk( 思维)的新内容,同时我们还将为您解释思维map的相关知识,另外,我们还将为您提供关于CF-Educational Codeforces Round 44 (Rated for Div. 2)-D-Sand Fortress、codeforces Educational Codeforces Round 49 (Rated for Div. 2) C题、Codeforces Educational Codeforces Round 67、codeforces educational round 76的实用信息。
本文目录一览:- Educational Codeforces Round 40 C. Matrix Walk( 思维)(思维map)
- CF-Educational Codeforces Round 44 (Rated for Div. 2)-D-Sand Fortress
- codeforces Educational Codeforces Round 49 (Rated for Div. 2) C题
- Codeforces Educational Codeforces Round 67
- codeforces educational round 76

Educational Codeforces Round 40 C. Matrix Walk( 思维)(思维map)
Educational Codeforces Round 40 (Rated for Div. 2)
C. Matrix Walk
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
There is a matrix A of size x?×?y filled with integers. For every


You have traversed some path in this matrix. Your path can be described as a sequence of visited cells a1,a2,...,*a**n* denoting that you started in the cell containing the number a1,then moved to the cell with the number a2,and so on.
From the cell located in i-th line and j-th column (we denote this cell as (i,?j)) you can move into one of the following cells:
- (i?+?1,?j) — only if i?<?x;
- (i,?j?+?1) — only if j?<?y;
- (i?-?1,?j) — only if i?>?1;
- (i,?j?-?1) — only if j?>?1.
Notice that making a move requires you to go to an adjacent cell. It is not allowed to stay in the same cell. You don‘t kNow x and y exactly,but you have to find any possible values for these numbers such that you Could start in the cell containing the integer a1,then move to the cell containing a2 (in one step),then move to the cell containing a3 (also in one step) and so on. Can you choose x and y so that they don‘t conTradict with your sequence of moves?
Input
The first line contains one integer number n (1?≤?n?≤?200000) — the number of cells you visited on your path (if some cell is visited twice,then it‘s listed twice).
The second line contains n integers a1,*a**n* (1?≤?*a**i*?≤?109) — the integers in the cells on your path.
Output
If all possible values of x and y such that 1?≤?x,?y?≤?109 conTradict with the information about your path,print NO.
Otherwise,print YES in the first line,and in the second line print the values x and y such that your path was possible with such number of lines and columns in the matrix. Remember that they must be positive integers not exceeding 109.
Examples
input
copy
81 2 3 6 9 8 5 2
output
copy
YES3 3
input
copy
61 2 1 2 5 3
output
copy
NO
input
copy
21 10
output
copy
YES4 9
Note
The matrix and the path on it in the first test looks like this:

Also there exist multiple correct answers for both the first and the third examples.
题意:
有一个很大的方格,x行,y列,以及a(i,j)=(i-1)*y+j
现在给你n个数的数组,代表在方格中只走相邻节点的路径经过的节点数值,,让你是否能确定一个x和y,如果有,则输出对应的x和y,否则输出no。
思路:
如果是一个合法的路径序列,那么相邻的节点的数值之差的绝对值只可能是1和y,
如果差的绝对值size有多个值(即大于2),或者有2个值但没有1,那么一定是不存在的。
接下来就是size<=2的情况了,
假设y=size 中较大的那一个(如果相等,即都为1,那么直接特判输出答案即可,),
去再从1到n扫check下如果y是该值,是否满足该序列,
注意一下情况:
当前在左边界num,向num-1走
当前在右边界num,向num+1走
都是不合法的(已经排除了y=1的情况)
然后输出即可。
get:一般给你一些信息,让你确定一些值的时候,一般还会问你是否不存在满足该信息的数值,如果是输出no,那么我们就可以在找到假设的数值之后,再去过一遍给的信息,判定是否信息和数值对的上。这是一个很好的处理方法和思路。
细节见代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(),(x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X),sizeof((X)))
#define MSC0(X) memset((X),'\0',sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) {return b ? gcd(b,a % b) : a;}
ll lcm(ll a,ll b) {return a / gcd(a,b) * b;}
ll powmod(ll a,ll b,ll MOD) {a %= MOD; if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d",V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld",V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
set<int> st;
int y = 0;
int a[maxn];
int ans1 = 1e9;
int n;
int main()
{
//freopen("D:\\code\\text\\input.txt","r",stdin);
//freopen("D:\\code\\text\\output.txt","w",stdout);
gbtb;
cin >> n;
repd(i,1,n)
{
cin >> a[i];
}
if (n == 1)
{
cout << "YES" << endl;
cout << ans1 << " " << 1 << endl;
return 0;
}
repd(i,2,n)
{
st.insert(abs(a[i] - a[i - 1]));
y = max(y,abs(a[i] - a[i - 1]));
if (a[i] == a[i - 1])
{
st.insert(10);
st.insert(11);
st.insert(14);
break;
}
}
if (st.size() > 2)
{
cout << "NO" << endl;
} else
{
if (st.size() == 2 && (*st.begin()) != 1)
{
cout << "NO" << endl;
}
else if (y == 1)
{
cout << "YES" << endl;
cout << ans1 << " " << 1 << endl;
} else
{
int isok = 1;
repd(i,n - 1)
{
int cha = a[i + 1] - a[i];
if ((a[i] % y) == 0 && cha == 1)
{
isok = 0;
break;
} else if ((a[i] % y) == 1 && cha == -1)
{
isok = 0;
break;
}
}
if (isok)
{
cout << "YES" << endl;
cout << ans1 << " " << y << endl;
} else
{
cout << "NO" << endl;
}
}
}
return 0;
}
inline void getInt(int* p) {
char ch;
do {
ch = getchar();
} while (ch == ' ' || ch == '\n');
if (ch == '-') {
*p = -(getchar() - '0');
while ((ch = getchar()) >= '0' && ch <= '9') {
*p = *p * 10 - ch + '0';
}
}
else {
*p = ch - '0';
while ((ch = getchar()) >= '0' && ch <= '9') {
*p = *p * 10 + ch - '0';
}
}
}

CF-Educational Codeforces Round 44 (Rated for Div. 2)-D-Sand Fortress
总结
以上是小编为你收集整理的CF-Educational Codeforces Round 44 (Rated for Div. 2)-D-Sand Fortress全部内容。
如果觉得小编网站内容还不错,欢迎将小编网站推荐给好友。

codeforces Educational Codeforces Round 49 (Rated for Div. 2) C题
- 刚开始拿到这题很懵逼,知道了别人的思路之后开始写,但是还是遇到很多坑,要求求P2/S最大。p=a b。就是求(a2+ b2 +2ab)/ab最大,也就是a/b +b/a最大。那么题意就很明显了。
但是处理的时候还要注意,刚开始用map存入数据,保存数量大于2的数据。接着就是找最小的,千万不要用数组进行双重循环查找,这样的O(n*n)会爆时,要先排序O(lgn);然后对相邻的遍历比较一遍就可以了O(n)。当数据量很大的时候差距很明显。
附上ac代码(java)
package codeforces504;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
/*
* 贪心 数学 排序
*/
public class testC {
public static void main(String[] args) throws IOException {
// TODO 自动生成的方法存根
StreamTokenizer in=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
in.nextToken();
int n=(int)in.nval;
for(int i=0;i<n;i++)
{
in.nextToken();int num=(int)in.nval;
int a[]=new int[num];
Map<Integer,Integer>map=new HashMap();
for(int j=0;j<num;j++)
{
in.nextToken();
int q=(int)in.nval;
if(map.containsKey(q)) {
map.put(q, map.get(q)+1);}
else map.put(q, 1);
}
int index=0;int a2=0;int b2=0;
boolean b=false;
for(int q:map.keySet())
{
if(map.get(q)>=4) {
a2=q;b2=q;b=true;break;}
else
if(map.get(q)>=2) {
a[index++]=q;}
}
if(!b) {
Arrays.sort(a,0, index);//0-到index-1排序
double min=Double.MAX_VALUE;;
for(int q=0;q<index-1;q++)
{
double d=(double)a[q]/(double)a[q+1]+(double)a[q+1]/(double)a[q];
if(d<min) {
min=d;a2=a[q];b2=a[q+1];}
}
}
out.println(a2+" "+a2+" "+b2+" "+b2);
out.flush();
}
}
}
本文分享 CSDN - Big sai。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。

Codeforces Educational Codeforces Round 67
[TOC]
Contest Info
<hr> Data:2019.6.30 Solved:4/7
##Solutions
<hr> ### A. Stickers and Toys
题意: 有 $A$ 物品 $s$ 个,$B$ 物品 $t$ 个,现在将这些物品装到 $n$ 个箱子里,每个箱子只有一下三种情况:
- 只有一个 $A$ 物品
- 只有一个 $B$ 物品
- 有一个 $A$ 物品和一个 $B$ 物品
现在问你,至少要取多少个箱子,能够保证你最少有一个 $A$ 物品和一个 $B$ 物品。
思路: 根据鸽笼原理,显然对于 $A$ 物品,至少取 $n - s + 1$ 个箱子就可以有一个 $A$ 物品。 同理,对于 $B$ 物品至少要取 $n - t + 1$ 个箱子。 答案就是 $Min (n - s +1, n - t + 1)$
代码:
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, s, t;
int T; scanf("%d", &T);
while (T--) {
scanf("%d%d%d", &n, &s, &t);
int res = max(n - s + 1, n - t + 1);
printf("%d\n", res);
}
return 0;
}
B. Letters Shop
题意: 有一个字符串 $s$,每次询问一个字符串 $t$,问最短的一个 $s$ 的前缀使得这个前缀中拥有的字符可以组成字符串 $t$。
思路一: 可以维护一个字符个数的前缀和,然后二分。
代码一:
#include <bits/stdc++.h>
using namespace std;
#define N 200010
int n, m, lens, lent;
char s[N], t[N];
int sum[N][27];
int cnt[27];
bool ok(int x) {
for (int i = 0; i < 26; ++i) {
if (sum[x][i] < cnt[i]) {
return 0;
}
}
return 1;
}
int main() {
while (scanf("%d", &n) != EOF) {
memset(sum, 0, sizeof sum);
scanf("%s", s + 1); lens = strlen(s + 1);
for (int i = 1; i <= lens; ++i) {
++sum[i][s[i] - ''a''];
for (int j = 0; j < 26; ++j) {
sum[i][j] += sum[i - 1][j];
}
}
scanf("%d", &m);
while (m--) {
scanf("%s", t + 1); lent = strlen(t + 1);
memset(cnt, 0, sizeof cnt);
for (int i = 1; i <= lent; ++i) {
++cnt[t[i] - ''a''];
}
int l = 1, r = n, res = -1;
while (r - l >= 0) {
int mid = (l + r) >> 1;
if (ok(mid)) {
r = mid - 1;
res = mid;
} else {
l = mid + 1;
}
}
printf("%d\n", res);
}
}
return 0;
}
思路二: 维护 $s$ 串中某类字符的第 $i$ 个所在位置,显然对于 $t$ 串中的每类字符有 $x$ 个的话,$s$ 串前缀的长度要大于等于这类字符第 $x$ 个所在的位置。
代码二:
#include <bits/stdc++.h>
using namespace std;
#define N 200010
int n, m, lens, lent;
char s[N], t[N];
int sum[N][27];
int cnt[27];
bool ok(int x) {
for (int i = 0; i < 26; ++i) {
if (sum[x][i] < cnt[i]) {
return 0;
}
}
return 1;
}
int main() {
while (scanf("%d", &n) != EOF) {
memset(sum, 0, sizeof sum);
scanf("%s", s + 1); lens = strlen(s + 1);
for (int i = 1; i <= lens; ++i) {
++sum[i][s[i] - ''a''];
for (int j = 0; j < 26; ++j) {
sum[i][j] += sum[i - 1][j];
}
}
scanf("%d", &m);
while (m--) {
scanf("%s", t + 1); lent = strlen(t + 1);
memset(cnt, 0, sizeof cnt);
for (int i = 1; i <= lent; ++i) {
++cnt[t[i] - ''a''];
}
int l = 1, r = n, res = -1;
while (r - l >= 0) {
int mid = (l + r) >> 1;
if (ok(mid)) {
r = mid - 1;
res = mid;
} else {
l = mid + 1;
}
}
printf("%d\n", res);
}
}
return 0;
}
C. Vasya And Array
题意: 要求构造一个数列 $a_1, \cdots, a_n$,使得满足 $m$ 个限制。 限制有两种类型:
- 1 l r 表示 $[l, r]$ 范围内的数是非降序的
- 0 l r 表示 $[l, r]$ 范围内的数不是非降序的
给出构造结果,或者输出‘NO’表示不存在这样的数列。
思路: 显然非降序的 $[l, r]$,我们可以全都赋为 $1$,但是最后一位可以不用赋为 $1$。 然后将没有赋为 $1$ 的地方降序赋值。 再考虑不是非降序的,只要满足这个区间内存在一个 $i$ 满足 $a_i > a_{i + 1}$ 即可。 只要 check 一下这些限制的区间内是否有这样一对即可。 否则输出 ''NO''
因为没考虑这样的对在最后一位的情况被 HACK 了。
代码:
#include <bits/stdc++.h>
using namespace std;
#define N 1010
int n, m;
int s[N];
struct node {
int t, l, r;
node() {}
void scan() {
scanf("%d%d%d", &t, &l, &r);
}
}a[N];
bool ok(int l, int r) {
for (int i = l; i <= r; ++i) {
if (s[i] == 0) {
return 1;
}
}
return 0;
}
bool check(node a) {
if (a.t == 1) {
for (int i = a.l + 1; i <= a.r; ++i) {
if (s[i - 1] > s[i]) {
return 0;
}
}
return 1;
} else {
for (int i = a.l + 1; i <= a.r; ++i) {
if (s[i - 1] > s[i]) {
return 1;
}
}
return 0;
}
}
void work() {
memset(s, 0, sizeof s);
for (int i = 1; i <= m; ++i) {
if (a[i].t == 1) {
++s[a[i].l];
--s[a[i].r];
}
}
for (int i = 1; i <= n; ++i) s[i] += s[i - 1];
for (int i = 1; i <= n; ++i) {
if (s[i]) s[i] = 1;
}
for (int i = 1; i <= m; ++i) {
if (a[i].t == 0) {
if (!ok(a[i].l, a[i].r)) {
puts("NO");
return;
}
}
}
int cnt = n;
for (int i = 1; i <= n; ++i) {
if (s[i] == 0) {
s[i] = cnt;
--cnt;
}
}
for (int i = 1; i <= m; ++i) {
if (!check(a[i])) {
puts("NO");
return;
}
}
puts("YES");
for (int i = 1; i <= n; ++i) printf("%d%c", s[i], " \n"[i == n]);
}
int main() {
while (scanf("%d%d", &n, &m) != EOF) {
for (int i = 1; i <= m; ++i) {
a[i].scan();
}
work();
}
return 0;
}
D. Subarray Sorting
题意: 给出两个数组 $a_1, \cdots, a_n$, $b_1, \cdots, b_n$,可以将 $a$ 数组进行不限次数的区间排序,问能够变成 $b$ 数组。
思路: 考虑从左往右移动 $a$ 中的数使得满足 $a_i = b_i$, 我们发现对于我们需要的 $a_i$,它能移动过来当且仅当它之前不存在比它小的数, 权值线段树维护一下即可。
代码:
#include <bits/stdc++.h>
using namespace std;
#define N 300010
int n, a[N], b[N];
int cnt[N], nx[N], f[N];
struct SEG {
int a[N << 2];
void build(int id, int l, int r) {
a[id] = 1e9;
if (l == r) return;
int mid = (l + r) >> 1;
build(id << 1, l, mid);
build(id << 1 | 1, mid + 1, r);
}
void update(int id, int l, int r, int pos, int x) {
if (l == r) {
a[id] = x;
return;
}
int mid = (l + r) >> 1;
if (pos <= mid) update(id << 1, l, mid, pos, x);
else update(id << 1 | 1, mid + 1, r, pos, x);
a[id] = min(a[id << 1], a[id << 1 | 1]);
}
int query(int id, int l, int r, int ql, int qr) {
if (ql > qr) return 1e9;
if (l >= ql && r <= qr) {
return a[id];
}
int mid = (l + r) >> 1;
int res = 1e9;
if (ql <= mid) res = min(res, query(id << 1, l, mid, ql, qr));
if (qr > mid) res = min(res, query(id << 1 | 1, mid + 1, r, ql, qr));
return res;
}
}seg;
bool work() {
for (int i = 1; i <= n; ++i) {
cnt[i] = 0;
}
for (int i = 1; i <= n; ++i) {
++cnt[a[i]];
--cnt[b[i]];
}
for (int i = 1; i <= n; ++i) {
if (cnt[i] != 0) {
return 0;
}
}
seg.build(1, 1, n);
for (int i = n; i >= 1; --i) {
nx[i] = n + 1;
}
for (int i = n; i >= 1; --i) {
f[i] = nx[a[i]];
nx[a[i]] = i;
}
// for (int i = 1; i <= n; ++i) {
// printf("%d %d\n", i, nx[i]);
// }
for (int i = 1; i <= n; ++i) {
seg.update(1, 1, n, i, nx[i]);
}
for (int i = 1; i <= n; ++i) {
if (seg.query(1, 1, n, 1, b[i] - 1) < nx[b[i]]) return 0;
nx[b[i]] = f[nx[b[i]]];
seg.update(1, 1, n, b[i], nx[b[i]]);
}
return 1;
}
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", a + i);
}
for (int i = 1; i <= n; ++i) {
scanf("%d", b + i);
}
puts(work() ? "YES" : "NO");
}
return 0;
}
E. Tree Painting
题意: 有一种树上游戏,刚开始每个点为黑点,第一次可以先选择一个点染白,之后每一次都可以选择一个与白点相邻的黑点将其染白,获得的分数为这个黑点所在的由黑点构成的连通块大小。 问在最优策略下获得的最大分数是多少?
思路: 考虑到根固定的话,选择的固定的,即每次从根往下取,而不是隔层取。 树形 DP 即可。
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 200010
int n;
vector <vector<int>> G;
int fa[N], sze[N];
ll f[N], g[N], res;
void DFS(int u) {
sze[u] = 1;
f[u] = 0;
for (auto v : G[u]) if (v != fa[u]) {
fa[v] = u;
DFS(v);
sze[u] += sze[v];
f[u] += f[v];
}
f[u] += sze[u];
}
void DFS2(int u) {
if (u == 1) {
g[u] = 0;
} else {
g[u] = g[fa[u]] + f[fa[u]] - f[u] - sze[u] + n - sze[fa[u]];
res = max(res, f[u] + g[u] - sze[u] + n);
}
for (auto v : G[u]) if (v != fa[u]) {
DFS2(v);
}
}
int main() {
while (scanf("%d", &n) != EOF) {
G.clear(); G.resize(n + 1);
for (int i = 1, u, v; i < n; ++i) {
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
DFS(1);
res = f[1];
DFS2(1);
printf("%lld\n", res);
}
return 0;
}

codeforces educational round 76
A. Two Rival Students
B. Magic Stick
C. Dominated Subarray
Description
给出一个序列串,求满足下述要求的最短子串序列。
- 子串序列内出现最多的元素有且仅有一种。
Solution
贪心思路:原序列相等的两个值最近的间距。
最开始想偏了,写了个滑窗,tle。
D. Yet Another Monster Killing Problem
Description

Solution
思路来自codeforces论讨赛后讨论
对英雄而言,求每种耐力对应最大的攻击力,并求前缀最大值。
那么有判断条件
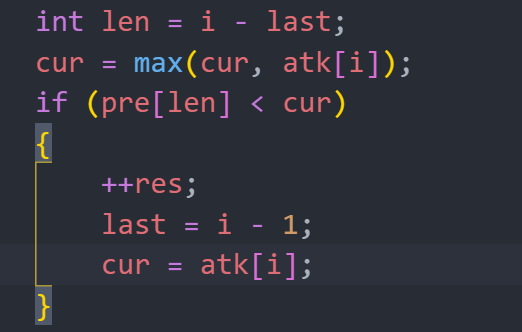
pre[i]代表耐力大于等于i的最大攻击值,c
F. Make Them Similar
Description
给定一个序列a,求一个数x使得a中每一个数与x异或后的二进制中1的个数相同。
Solution
看了题解发现了一种记录两个数组对应索引项之和是否相等的骚操作。
如对于$a=\{1,2,3,4,7\},b=\{7,6,5,4,1\}$
求a中数据全部减去a[0]后的值$a^1=\{0,1,2,3,6\}$
求b中数据全部被b[0]减去后的值$b^1=\{0,1,2,3,6\}$
发现$a^1=b^1$,那么就可以知道a+b中元素都相等。
回到本题,枚举每一个$x\ in\ [0,2^{30}-1]$显然复杂度炸裂,那么可以采用meet in the middle的方法。
先枚举高位再枚举低位,反过来亦可。
利用map对类差分序列进行记录。


1 #include <algorithm>
2 #include <cctype>
3 #include <cmath>
4 #include <cstdio>
5 #include <cstdlib>
6 #include <cstring>
7 #include <iostream>
8 #include <map>
9 #include <numeric>
10 #include <queue>
11 #include <set>
12 #include <stack>
13 #if __cplusplus >= 201103L
14 #include <unordered_map>
15 #include <unordered_set>
16 #endif
17 #include <vector>
18 #define lson rt << 1, l, mid
19 #define rson rt << 1 | 1, mid + 1, r
20 #define LONG_LONG_MAX 9223372036854775807LL
21 #define pblank putchar('' '')
22 #define ll LL
23 #define fastIO ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
24 using namespace std;
25 typedef long long ll;
26 typedef long double ld;
27 typedef unsigned long long ull;
28 typedef pair<int, int> P;
29 int n, m, k;
30 const int maxn = 1e5 + 10;
31 template <class T>
32 inline T read()
33 {
34 int f = 1;
35 T ret = 0;
36 char ch = getchar();
37 while (!isdigit(ch))
38 {
39 if (ch == ''-'')
40 f = -1;
41 ch = getchar();
42 }
43 while (isdigit(ch))
44 {
45 ret = (ret << 1) + (ret << 3) + ch - ''0'';
46 ch = getchar();
47 }
48 ret *= f;
49 return ret;
50 }
51 template <class T>
52 inline void write(T n)
53 {
54 if (n < 0)
55 {
56 putchar(''-'');
57 n = -n;
58 }
59 if (n >= 10)
60 {
61 write(n / 10);
62 }
63 putchar(n % 10 + ''0'');
64 }
65 template <class T>
66 inline void writeln(const T &n)
67 {
68 write(n);
69 puts("");
70 }
71 template <typename T>
72 void _write(const T &t)
73 {
74 write(t);
75 }
76 template <typename T, typename... Args>
77 void _write(const T &t, Args... args)
78 {
79 write(t), pblank;
80 _write(args...);
81 }
82 template <typename T, typename... Args>
83 inline void write_line(const T &t, const Args &... data)
84 {
85 _write(t, data...);
86 }
87 const int bit = 15;
88 map<vector<int>, int> mp;
89 int a[maxn];
90 int main(int argc, char const *argv[])
91 {
92 #ifndef ONLINE_JUDGE
93 freopen("in.txt", "r", stdin);
94 // freopen("out.txt", "w", stdout);
95 #endif
96 n = read<int>();
97 for (int i = 0; i < n; i++)
98 a[i] = read<int>();
99 mp.clear();
100 int tmp = 1 << bit;
101 for (int i = 0; i < tmp; i++)
102 {
103 vector<int> cur(n);
104 for (int j = 0; j < n; j++)
105 cur[j] = __builtin_popcount((a[j] & (tmp - 1)) ^ i);
106 for (int j = n - 1; j >= 0; j--)
107 cur[j] -= cur[0];
108 mp[cur] = i;
109 }
110 int f = 0;
111 for (int i = 0; i < tmp && !f; i++)
112 {
113 vector<int> cur(n);
114 for (int j = 0; j < n; j++)
115 cur[j] = __builtin_popcount((a[j] >> bit) ^ i);
116 for (int j = n - 1; j >= 0; j--)
117 cur[j] = cur[0] - cur[j];
118 if (mp.count(cur))
119 {
120 f = 1;
121 writeln((i << bit) | mp[cur]);
122 }
123 }
124 if (!f)
125 puts("-1");
126 return 0;
127 }
我们今天的关于Educational Codeforces Round 40 C. Matrix Walk( 思维)和思维map的分享就到这里,谢谢您的阅读,如果想了解更多关于CF-Educational Codeforces Round 44 (Rated for Div. 2)-D-Sand Fortress、codeforces Educational Codeforces Round 49 (Rated for Div. 2) C题、Codeforces Educational Codeforces Round 67、codeforces educational round 76的相关信息,可以在本站进行搜索。
本文标签:





