GVKun编程网logo

数组中的逆序对(python)（数组中的逆序对java）

3

在本文中，您将会了解到关于数组中的逆序对(python)的新资讯，同时我们还将为您解释数组中的逆序对java的相关在本文中，我们将带你探索数组中的逆序对(python)的奥秘，分析数组中的逆序对jav

在本文中，您将会了解到关于数组中的逆序对(python)的新资讯，同时我们还将为您解释数组中的逆序对java的相关在本文中，我们将带你探索数组中的逆序对(python)的奥秘，分析数组中的逆序对java的特点，并给出一些关于Error: Can‘t find Python executable “python“, you can set the PYTHON env variable、JZ-035-数组中的逆序对、LeetCode 面试题51. 数组中的逆序对、python / beautifulsoup查找[具有特定锚文本的](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)所有[内容](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)的实用技巧。

本文目录一览：

数组中的逆序对(python)（数组中的逆序对java）

数组中的逆序对(python)（数组中的逆序对java）

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述:

题目保证输入的数组中没有的相同的数字

数据范围：

对于%50的数据,size<=10^4

对于%75的数据,size<=10^5

对于%100的数据,size<=2*10^5

示例1

输入

复制 
1,2,3,4,5,6,7,0

输出

复制 
7
# -*- coding:utf-8 -*-
class Solution:
    def InversePairs(self, data):
        # write code here
        #用归并排序，归并拼接后用计算排序时元素的index变动了少
        _,s=self.MergeSort(data)
        return s%1000000007
    def MergeSort(self,data):
        n=len(data)
        #递归基
        if n==1:return data, 0
        #分两半来排序
        part1,part2=data[:n//2],data[n//2:]
        sorted_part1,s1=self.MergeSort(part1)
        sorted_part2,s2=self.MergeSort(part2)
        #排序后拼接这两半，拼接后先计数，然后将两个有序序列合并
        s,sorted_temp=0,sorted_part1+sorted_part2
        #用p、q两个指针指向两段，计算q中每个元素离插入点的index差
        p,q,len1,len_all=0,sorted_temp.index(sorted_part2[0]),len(sorted_part1),len(sorted_temp)
        while p<len1 and q<len_all:
            #移动p使p成为插入排序的插入点，计算要移动多少个位置
            while p<len1:
                if sorted_temp[q]<sorted_temp[p]:
                    s+=len1-p
                    break
                p+=1
            q+=1
        #完成排序，并把排序后的内容回溯给上一级做准备
        l=[]
        p,q=0,sorted_temp.index(sorted_part2[0])
        while p<len1 and q<len_all:
            if sorted_temp[p]<sorted_temp[q]:
                l.append(sorted_temp[p])
                p+=1
            else:
                l.append(sorted_temp[q])
                q+=1
        if p==len1:l+=sorted_temp[q:]
        if q==len_all:l+=sorted_part1[p:]
        return l,s+s1+s2

　　

Error: Can‘t find Python executable “python“, you can set the PYTHON env variable

Error: Can‘t find Python executable “python“, you can set the PYTHON env variable

在启动vue项目的时候，安装node.js组件node-sass过程中报错了，错误提示如下
Error: Can’t find Python executable “python”, you can set the PYTHON env variable

由错误提示可知：Node.js 在安装模块组件node-sass的时候，node.js缺少Visual Studio2015 Build Tools相关的组件和python的环境，如果安装了vs2015组件的小伙伴们就不用安装Visual Studio2015 Build Tools相应的组件，只用安装python2.7即可解决缺少的python组件的问题。

欲安装python2.7，请至python官网：www.python.org 下载，然后配置好python的环境变量即可。

不过博主我并不推荐上述的解决方案，因为对于程序员来说，效率第一，上述的问题一个命令就可以轻松解决你所遇到的麻烦，前面说了那么多，无非就是想告诉在看本篇博客的同仁们放下浮躁的心，遇到问题首先不是急着去解决问题，而是分析为什么会这样，然后才能水到聚成的去找到解决问题的方法。

运行下面这个命令即可解决你们遇到的Error问题

npm install --global --production windows-build-tools

注：上面讲述了一堆就是为了讲述此命令是干嘛的，上面已经描述很详细了，就不再赘述了，该操作与上述的一堆操作无异，效果却是一样的。

然后运气不好的小伙伴可能接着会遇到一个坑，那就是执行了：npm install --global --production windows-build-tools这个命令的人细心点会发现执行到一半就卡住了，这个卡住了没有红字重点提示，而且下方还有英文在等待中，粗心的小伙伴可能以为是命令执行完了，组件安装好了，其实不然，我这边已经解决了，就无法复现了，具体点就是中文的提示，提示我们由于有类似组件在运行或者下载导致无法继续下载安装组件了。稳妥点的解决办法是，将电脑重启，将底层正在运行的模块干掉，待电脑重启后再执行npm install --global --production windows-build-tools这条命令即可，博主我就是这样解决的，稳稳的幸福就会浮现在你面前如下图所示，你的可能和我不一样，因为我已经跑成功过一次了，没有你的那么多细节的log打印。
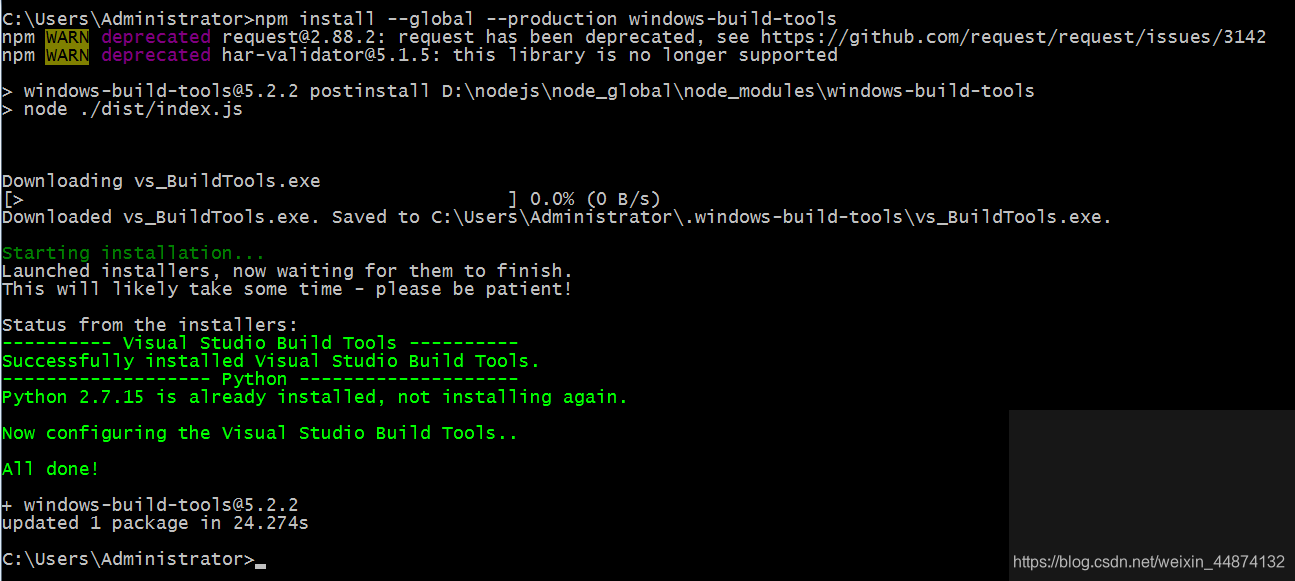
在这里插入图片描述

然后就是在你的项目下shift+鼠标右击你的项目运行npm run dev即可启动vue项目了。

JZ-035-数组中的逆序对

JZ-035-数组中的逆序对

数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

题目链接: 数组中的逆序对

代码

/**
 * 标题：数组中的逆序对
 * 题目描述
 * 在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
 * 题目链接：
 * https://www.nowcoder.com/practice/96bd6684e04a44eb80e6a68efc0ec6c5?tpId=13&&tqId=11188&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
 */
public class Jz35 {

    private long cnt = 0;
    private int[] tmp; // 在这里声明辅助数组，而不是在 merge() 递归函数中声明

    public int inversePairs(int[] array) {
        tmp = new int[array.length];
        mergeSort(array, 0, array.length - 1);
        return (int) (cnt % 1000000007);
    }

    private void mergeSort(int[] nums, int l, int h) {
        if (h - l < 1) {
            return;
        }
        int m = l + (h - l) / 2;
        mergeSort(nums, l, m);
        mergeSort(nums, m + 1, h);
        merge(nums, l, m, h);
    }

    private void merge(int[] nums, int l, int m, int h) {
        int i = l, j = m + 1, k = l;
        while (i <= m || j <= h) {
            if (i > m) {
                tmp[k] = nums[j++];
            } else if (j > h) {
                tmp[k] = nums[i++];
            } else if (nums[i] <= nums[j]) {
                tmp[k] = nums[i++];
            } else {
                tmp[k] = nums[j++];
                this.cnt += m - i + 1; // nums[i] > nums[j]，说明 nums[j..mid] 都大于 nums[j]
            }
            k++;
        }
        for (k = l; k <= h; k++) {
            nums[k] = tmp[k];
        }
    }

    public static void main(String[] args) {
        
    }
}
【每日寄语】 每一天都是全新的开始，每一天都会有最好的运气。

LeetCode 面试题51. 数组中的逆序对

LeetCode 面试题51. 数组中的逆序对

面试题51. 数组中的逆序对

题目来源：https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/

题目

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

解题思路

思路：归并排序

归并排序使用了分治的思想，这个过程需要使用递归来实现。在分治算法递归实现中，每层递归会涉及三个步骤：

  • 分解：将原问题分解为一系列子问题；
  • 解决：递归求解各个子问题，若子问题足够小，直接求解；
  • 合并：将子问题的结果合并为原问题。

在本题当中，

  • 分解：假设区间为 [left, right]，令 mid = [(left + right) / 2]，将 [left, right] 分成 [left, mid] 和 [mid + 1, right]；
  • 解决：使用递归排序两个子序列；
  • 合并：将已经排好的子序列 [left, mid] 和 [mid + 1, right] 合并

题目中要求返回数组构成逆序对的总数。逆序对：即是前面的一个数字大于后面的数字，那么这两个数字可以构成一个逆序对。

具体思想参考代码。

代码实现

class Solution:
    def reversePairs(self, nums: List[int]) -> int:
        n = len(nums)
        if n < 2:
            return 0
        # 辅助数组，用于归并
        temp = [0] * n
        return self.count_invs(nums, 0, n - 1, temp)
    
    def count_invs(self, nums, left, right, temp):
        if left == right:
            return 0
        
        mid = (left + right) // 2
        left_pairs = self.count_invs(nums, left, mid, temp)
        right_pairs = self.count_invs(nums, mid+1, right, temp)
        # 这里表示已经排序好，并且已经计算左右两部分未排序前的逆序对
        invs_pairs = left_pairs + right_pairs

        if nums[mid] < nums[mid + 1]:
            # 这个时候表示都是顺序排序，不用计算两个区间交叉的逆序对，直接返回
            return invs_pairs
        
        # 这里计算区间交叉的逆序对
        invs_cross_pairs = self.merge_count(nums, left, mid, right, temp)

        return invs_pairs + invs_cross_pairs
    
    def merge_count(self, nums, left, mid, right, temp):
        # 现在两个区间都是有序的
        # 合并计算此时区间交叉的逆序对个数
        # 复制原数组到辅助数组
        for i in range(left, right + 1):
            temp[i] = nums[i]
        
        p = left
        q = mid + 1
        ans = 0
        for i in range(left, right + 1):
            # 这里归并剩余的部分
            if p > mid:
                nums[i] = temp[q]
                q += 1
            elif q > right:
                nums[i] = temp[p]
                p += 1
            elif temp[p] <= temp[q]:
                # 这个时候，前面部分区间的元素出列
                # 因为 p 对应的元素，比 q 对应的元素小
                # 那么 p 对应的元素一定比 q 对应元素后面的元素都小
                # 所以这个时候不统计逆序对，p 往前移动
                nums[i] = temp[p]
                p += 1
            else:
                # 这种属于相反的情况
                # p 对应的元素比 q 对应的元素大，
                # 那么 p 对应的元素后面的元素一定更大
                # 所以，元素出列同时统计逆序对
                # 这个时候，数组位置 p 到该区间末尾有多少个元素就有多少个逆序对，即是 mid - p + 1
                nums[i] = temp[q]
                q += 1
                ans += (mid - p + 1)
        
        return ans

实现结果

实现结果

以上就是使用归并排序的思想，解决《面试题51. 数组中的逆序对》问题的主要内容。
欢迎关注微信公众号《书所集录》

python / beautifulsoup查找[具有特定锚文本的](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)所有[内容](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)

python / beautifulsoup查找[具有特定锚文本的](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)所有[内容](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)

[

我正在尝试使用漂亮的汤来解析html并找到具有特定锚标记的所有href

<a href="http://example.com">TEXT</a><a href="http://example.com/link">TEXT</a><a href="http://example.com/page">TEXT</a>

我要查找的所有链接都具有完全相同的锚文本，在本例中为TEXT。我不是在寻找单词TEXT，而是想使用单词TEXT查找所有不同的HREF

编辑：

为了澄清，寻找类似于使用类解析链接的内容

<a href="http://example.com">TEXT</a><a href="http://example.com/link">TEXT</a><a href="http://example.com/page">TEXT</a>

然后使用

findAll(''a'', ''visible'')

除了我正在解析的HTML没有一个类，而是总是相同的锚文本

](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)

答案1

小编典典

[

这样的事情行吗？

In [39]: from bs4 import BeautifulSoupIn [40]: s = """\   ....: <a href="http://example.com">TEXT</a>   ....: <a href="http://example.com/link">TEXT</a>   ....: <a href="http://example.com/page">TEXT</a>   ....: <a href="http://dontmatchme.com/page">WRONGTEXT</a>"""In [41]: soup = BeautifulSoup(s)In [42]: for link in soup.findAll(''a'', href=True, text=''TEXT''):   ....:     print link[''href'']   ....:   ....:http://example.comhttp://example.com/linkhttp://example.com/page

](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)

今天关于数组中的逆序对(python)和数组中的逆序对java的分享就到这里，希望大家有所收获，若想了解更多关于Error: Can‘t find Python executable “python“, you can set the PYTHON env variable、JZ-035-数组中的逆序对、LeetCode 面试题51. 数组中的逆序对、python / beautifulsoup查找[具有特定锚文本的](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)所有[内容](file:///C:/Users/Jiang/Desktop/spider/pages/python/page_750_08.html)等相关知识，可以在本站进行查询。

本文标签：

上一篇python 的进程与线程（二）（python中的进程和线程）

下一篇Python+Selenium+Unittest 框架使用 ——Selenium—— 定位元素（二）（python selenium定位元素方法）

相关文章