对于哈尔滨手机seo(哈尔滨手机回收)感兴趣的读者,本文将提供您所需要的所有信息,我们将详细讲解哈尔滨手机回收电话,并且为您提供关于"科林明伦杯"哈尔滨理工大学第八届程序设计竞赛题解、2017CCPC
对于哈尔滨手机seo(哈尔滨手机回收)感兴趣的读者,本文将提供您所需要的所有信息,我们将详细讲解哈尔滨手机回收电话,并且为您提供关于"科林明伦杯" 哈尔滨理工大学第八届程序设计竞赛 题解、2017 CCPC 哈尔滨、2017CCPC 哈尔滨 B、2020哈尔滨php培训哪里好?的宝贵知识。
本文目录一览:
哈尔滨手机seo(哈尔滨手机回收)(哈尔滨手机回收电话)
1. 哈尔滨手机回收
您好目前电信手机卡过户需要双方持身份证到当地营业厅才能办理的,如果没有原机主是不能过户的。
2. 哈尔滨手机回收机器
哈尔滨最大的手机卖场以前是华滨通讯航母,宣传口号是选来选去选华滨,当时是别的手机卖场和他没法比,大家买手机都认准来华滨买。但近几年随着时间推移,大家在网上买的比较多了,华滨也渐渐地消退了,目前七星手机连锁卖场在哈尔滨比较火,宣传的力度也比较大。
3. 哈尔滨手机回收门店
是大型综合商场,有手机。
4. 哈尔滨手机回收价格
就是13333333333。前阵子网上都报道了。
日前,“1333333尊贵吉祥号大礼包全国竞买会”落下帷幕,作为目前最长的手机连号13333333333,在竞买来宾的激烈角逐后,最终以182万元的天价被一北京男子买走,其他9个吉祥号也以高价成交。
5. 哈尔滨手机回收市场在哪
百脑汇对面的工大电子商城有换电池芯的这个我去过还有在和兴路和兴商城对面(立交桥头)有一个店铺写着专业换笔记本手机电池芯牌子很大容易找这个我没去过教化里面也有~
6. 哈尔滨手机回收报价表
哈尔滨手机卖场主要有:华滨、凌志、新天天、北斗星正规卖场:华滨、凌志;一般买手机都去这,售后有保证;讲价一般只能多要些小赠品;北斗星价格最优,但是传闻手机一般;建议:自己亲自挑选,去哈尔滨南岗“秋林”,所有卖场在秋林都有店,而且坐车公交方便,华滨2家,凌志n多家,花园街恒运大厦有北斗星,花园街还有苏宁电器,北方剧场有新天天,大世界3楼还有二手山寨手机等。
7. 哈尔滨手机号码回收
在远大购物中心一楼有专柜。现在远大在搞返券,施华洛世奇有些也参加,你可以去看看。
8. 哈尔滨哪里回收手机
哈尔滨有很多卖场都可以购买到安卓手机。比如你可以在哈尔滨找到很多家国美黑天鹅电器。苏宁电器。7星手机连锁。凌志手机连锁。包括很多,比如说联通电信的营业厅也会销售安卓手机。
9. 哈尔滨手机回收电话
电话卡可以异地补办,可由本人携带第二代身份证,到相关公司指定的营业厅进行办理跨区补卡服务。SIM卡是GSM系统移动用户持有的智能卡,可以在不同的手机上使用,也称为用户识别卡。SIM卡主要用于存储用户识别数据、短信数据和电话号码。GSM手机只能用这张卡。一旦SIM卡从手机上拔下,手机将无法享受网络运营商提供的各种服务,紧急呼叫除外。
10. 哈尔滨手机回收市场
自己上网买屏去手机店换给手续费最划算,有的自己就能换,我的就自己换的

"科林明伦杯" 哈尔滨理工大学第八届程序设计竞赛 题解
题目链接 Problems
Problem A
快速幂累加即可。
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
LL ans = 0;
LL n, d;
int T;
const LL mod = 1e9 + 7;
inline LL Pow(LL a, LL b, LL Mod){
LL ret(1);
for (; b; b >>= 1, (a *= a) %= Mod) if (b & 1) (ret *= a) %= Mod;
return ret;
}
int main(){
scanf("%d", &T);
while (T--){
cin >> n >> d;
ans = 0;
rep(i, 1, n){
ans += Pow(i, d, mod);
ans %= mod;
}
printf("%lld\n", ans);
}
return 0;
}
Problem B
对于每个帮派,并查集维护就可以了。
求第 $k$ 大的时候树状数组上二分就好了。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
const int N = 1e5 + 10;
int T;
int sz[N], c[N], father[N];
int n, m;
int num;
void update(int x, int val){
for (; x <= n; x += x & -x) c[x] += val;
}
int query(int x){
int ret = 0;
for (; x; x -= x & -x) ret += c[x];
return ret;
}
int getfather(int x){
return father[x] == x ? x : father[x] = getfather(father[x]);
}
int main(){
scanf("%d", &T);
while (T--){
scanf("%d%d", &n, &m);
memset(c, 0, sizeof c);
memset(father, 0, sizeof father);
rep(i, 1, n) father[i] = i;
rep(i, 1, n) update(1, 1);
num = n;
rep(i, 1, n) sz[i] = 1;
while (m--){
int op;
scanf("%d", &op);
if (op == 1){
int x, y;
scanf("%d%d", &x, &y);
int fx = getfather(x), fy = getfather(y);
if (fx == fy) continue;
father[fy] = fx;
int f1 = sz[fx], f2 = sz[fy], f3 = sz[fx] + sz[fy];
sz[fx] += sz[fy];
sz[fy] = 0;
--num;
update(f1, -1);
update(f2, -1);
update(f3, 1);
}
else{
int x;
scanf("%d", &x);
if (num < x){
puts("-1");
continue;
}
int l = 1, r = n;
while (l + 1 < r){
int mid = (l + r) >> 1;
if (num - query(mid - 1) >= x) l = mid;
else r = mid - 1;
}
if (num - query(r - 1) >= x) printf("%d\n", r);
else printf("%d\n", l);
}
}
}
return 0;
}
Problem C
递推。$f_{n} = 2f_{n-1} + f_{n-3}$
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
const int A = 5;
const LL mod = 1e9 + 7;
struct matrix{ LL a[A][A];} init, unit, aa;
int n;
LL m;
int T;
matrix Mul(matrix a, matrix b){
matrix c;
rep(i, 1, n) rep(j, 1, n){
c.a[i][j] = 0;
rep(k, 1, n) (c.a[i][j] += (a.a[i][k] * b.a[k][j] % mod)) %= mod;
}
return c;
}
matrix Pow(matrix a, LL k){
matrix ret(unit); for (; k; k >>= 1ll, a = Mul(a, a)) if (k & 1) ret = Mul(ret, a); return ret;
}
int main(){
n = 3;
matrix dd;
memset(dd.a, 0, sizeof dd.a);
memset(unit.a, 0, sizeof unit.a);
rep(i, 1, n) unit.a[i][i] = 1ll;
dd.a[1][1] = 2; dd.a[1][2] = 0; dd.a[1][3] = 1;
dd.a[2][1] = 1;
dd.a[3][2] = 1;
scanf("%d", &T);
while (T--){
scanf("%lld", &m);
LL fuck = m - 3;
if (m <= 3){
if (m == 1ll) puts("1");
if (m == 2ll) puts("2");
if (m == 3ll) puts("5");
continue;
}
matrix cc = Pow(dd, fuck);
LL ans = cc.a[1][1] * 5ll + cc.a[1][2] * 2ll + cc.a[1][3] * 1ll;
ans %= mod;
printf("%lld\n", ans);
}
return 0;
}
Problem D
最坏的情况即为斐波那契数列中的某几项。
那么当询问元素个数超过一定的时候(大概 $87$)直接输出 Yes 就好了。
否则就暴力特判。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
LL a[100010];
LL c[100010];
int n, q;
int cnt = 0;
int main(){
scanf("%d", &n);
rep(i, 1, n) scanf("%lld", a + i);
scanf("%d", &q);
while (q--){
int l, r;
scanf("%d%d", &l, &r);
if (r - l + 1 >= 100){
puts("Yes");
continue;
}
cnt = 0;
rep(i, l, r) c[++cnt] = a[i];
sort(c + 1, c + cnt + 1);
int fg = 0;
rep(i, 1, cnt - 2) if (c[i] + c[i + 1] > c[i + 2]){
fg = 1;
break;
}
puts(fg ? "Yes" : "No");
}
return 0;
}
Problem E
分解质因数之后令 $a_{i}$ 为每个质因数的指数。
答案为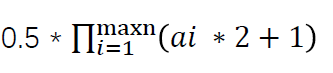
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
LL n;
int T;
LL bs;
LL cc;
LL ans;
int main(){
while (~scanf("%d", &T)){
while (T--){
scanf("%lld", &n);
LL bs = sqrt(n);
ans = 1;
for (LL i = 2; i <= sqrt(n); ++i){
LL cc = 0;
while (n % i == 0) ++cc, n /= i;
ans *= (2 * cc + 1ll);
}
if (n > 1) ans *= 3;
++ans;
ans /= 2;
printf("%lld\n", ans);
}
}
return 0;
}
Problem F
答案为 $2^{n-3} * n^{2} * (n+3)$
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
const LL mod = 1e9 + 7;
int T;
LL n, ans;
inline LL Pow(LL a, LL b, LL Mod){
LL ret(1);
for (; b; b >>= 1, (a *= a) %= Mod) if (b & 1) (ret *= a) %= Mod;
return ret;
}
int main(){
scanf("%d", &T);
while (T--){
scanf("%lld", &n);
if (n == 1ll){
puts("1");
continue;
}
if (n == 2ll){
puts("10");
continue;
}
if (n == 3ll){
puts("54");
continue;
}
LL ans = Pow(2, n - 3, mod);
ans *= n;
ans %= mod;
ans *= n;
ans %= mod;
ans *= (n + 3ll);
ans %= mod;
printf("%lld\n", ans);
}
return 0;
}
Problem G
从小到大枚举答案,每次做一遍极大极小搜索,若符合题意就直接输出。
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
const int N = 2e3 + 10;
LL a[N];
LL f[2][N];
LL s[N];
LL xxx;
int n;
int m;
int ans;
LL dp(int x, int pos){
if (~f[x][pos]) return f[x][pos];
if (pos == m){
if (x) return f[x][pos] = a[pos];
else return f[x][pos] = 0;
}
LL ret = 0;
if (x){
ret = a[pos] + dp(x ^ 1, pos + 1);
ret = max(ret, dp(x, pos + 1));
}
else{
ret = dp(x ^ 1, pos + 1);
ret = min(ret, a[pos] + dp(x, pos + 1));
}
return f[x][pos] = ret;
}
int main(){
while (~scanf("%d", &n) && n != -1){
rep(i, 1, n) scanf("%lld", a + i);
scanf("%lld", &xxx);
s[0] = 0;
rep(i, 1, n) s[i] = s[i - 1] + a[i];
ans = -1;
for (m = 1; m <= n; ++m){
memset(f, -1, sizeof f);
LL gg = dp(1, 1);
if (gg >= xxx){
ans = m;
break;
}
}
printf("%d\n", ans);
}
return 0;
}
Problem H
贪心。求出每个块的大小,然后枚举每个块。记块的个数为 $cnt$
两边的块如果有不小于 $2$ 的,那么答案用 $cnt + 1$ 更新。
中间的块大小如果有不小于 $3$ 的,那么答案用 $cnt + 2$ 更新。
UPD:哦草我好像没考虑 0011 然后翻转中间的 0 和 1 的情况,这也是一个 case
代码就不改乐
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
const int N = 1e5 + 10;
int a[N];
int c[N];
int n, cnt, xx, now;
int ans;
int main(){
while (~scanf("%d", &n)){
rep(i, 1, n) scanf("%1d", a + i);
xx = -1;
cnt = -1; now = 0;
rep(i, 1, n){
if (a[i] != xx){
c[++cnt] = now;
now = 1;
}
else ++now;
xx = a[i];
}
c[++cnt] = now;
ans = cnt;
if (c[1] == 2 || c[cnt] == 2) ans = max(ans, cnt + 1);
rep(i, 1, cnt) if (c[i] >= 3) ans = max(ans, cnt + 2);
printf("%d\n", ans);
}
return 0;
}Problem I
模拟题。
#include <cstdio>
#include <set>
#include <string>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
char s[11010];
int T;
set <string> mp;
int l;
int n;
set <string> :: iterator it;
int judge(char ch){
if ((ch >= ''a'' && ch <= ''z'') || (ch >= ''A'' && ch <= ''Z'') || (ch >= ''0'' && ch <= ''9'') || (ch == ''-'') || (ch == ''_'')) return 1;
return 0;
}
int main(){
scanf("%d", &T);
while (T--){
mp.clear();
scanf("%d", &n);
getchar();
rep(op, 1, n){
gets(s);
l = strlen(s);
string s1 = "";
int i;
for (i = 0; i < l; ++i){
if (s[i] == ''@''){
if (i && judge(s[i - 1])) continue;
s1 = "";
for (; i + 1 < l && judge(s[i + 1]); ){
s1 += s[i + 1];
++i;
}
if (s1 != "") mp.insert(s1);
}
}
}
printf("%d\n", (int)mp.size());
for (it = mp.begin(); it != mp.end(); ++it) cout << *it << endl;
}
return 0;
}
Problem J
签到。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
#define MP make_pair
#define fi first
#define se second
typedef long long LL;
int a[100010], b[100010];
int n ;
int T;
int main(){
scanf("%d", &T);
while (T--){
scanf("%d", &n);
rep(i, 1, n) scanf("%d", a + i);
rep(i, 1, n) scanf("%d", b + i);
int ff = 1, fg = 1;
rep(i, 1, n) if (a[i] > b[i]) ff = 0;
rep(i, 1, n) if (a[i] > b[n - i + 1]) fg = 0;
if (ff && fg) puts("both");
else if (ff && !fg) puts("front");
else if (!ff && fg) puts("back");
else puts("none");
}
return 0;
}

2017 CCPC 哈尔滨
A. 3:20:22(-1) solved by hl
WA点:三年竞赛一场空,不开LL见祖宗
由题意化为 要求左右两回文串都是奇数长度且相互覆盖对方的回文串中点。
用Manacher预处理之后 对于每个回文串x产生的后效性,在经过中点i的时候加入树状数组,经过终点i + Mp[i] + 1的移出树状数组
对于每个中点为i回文串作为后边那个产生的贡献,将所有中点位于 i + Mp[i] - 1 到 i - 1的回文串计出贡献
树状数组负责维护后缀和


#include <map>
#include <set>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <bitset>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
#define For(i, x, y) for(int i=x;i<=y;i++)
#define _For(i, x, y) for(int i=x;i>=y;i--)
#define Mem(f, x) memset(f,x,sizeof(f))
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%lld",&x)
#define Pri(x) printf("%d\n", x)
#define Prl(x) printf("%lld\n",x)
#define CLR(u) for(int i=0;i<=N;i++)u[i].clear();
#define LL long long
#define ULL unsigned long long
#define mp make_pair
#define PII pair<int,int>
#define PIL pair<int,long long>
#define PLL pair<long long,long long>
#define pb push_back
#define fi first
#define se second
typedef vector<int> VI;
int read(){int x = 0,f = 1;char c = getchar();while (c<''0'' || c>''9''){if (c == ''-'') f = -1;c = getchar();}
while (c >= ''0''&&c <= ''9''){x = x * 10 + c - ''0'';c = getchar();}return x*f;}
const double PI = acos(-1.0);
const double eps = 1e-9;
const int maxn = 5e5 + 10;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
int N,M,K;
char str[maxn];
char Ma[maxn << 1];
int Mp[maxn <<1];
void Manacher(char s[],int len){
int l = 0;
Ma[l++] = ''$'';
Ma[l++] = ''#'';
for(int i = 0 ; i < len; i ++){
Ma[l++] = s[i];
Ma[l++] = ''#'';
}
Ma[l] = 0;
int mx = 0,id = 0;
for(int i = 0 ; i < l; i ++){
Mp[i] = mx > i?min(Mp[2 * id - i],mx - i):1;
while(Ma[i + Mp[i]] == Ma[i - Mp[i]]) Mp[i]++;
if(i + Mp[i] > mx){
mx = i + Mp[i];
id = i;
}
}
}
vector<int>Q[maxn * 2];
LL tree[maxn * 2],l;
void add(int p,int x){
for(;p > 0; p -= p & -p) tree[p] += x;
}
LL getsum(int p){
if(!p) p ++;
LL ans = 0;
for(;p <= 2 * l + 2; p += p & -p) ans += tree[p];
return ans;
}
int main(){
int T; Sca(T);
while(T--){
scanf("%s",str);
l = strlen(str);
Manacher(str,l);
LL ans = 0;
for(int i = 0 ; i < 2 * l + 2; i ++) Q[i].clear();
for(int i = 0 ; i <= 2 * l + 2; i ++) tree[i] = 0;
for(int i = 2; i < 2 * l + 2; i += 2){
Mp[i]--;
ans += getsum(i - Mp[i] + 1);
if(Mp[i] > 1){
Q[i + Mp[i] - 1].pb(i);
add(i,1);
}
for(int j = 0 ; j < Q[i].size(); j ++){
add(Q[i][j],-1);
}
Q[i].clear();
}
Prl(ans);
}
return 0;
}
/*
*/
B.3:44:10(-1) solved by hl
二分最终答案,将原序列大于等于二分值的视为1,剩下的视为0
那么满足条件的区间的个数就是所有序列中区间和 >= K的区间的个数
线性时间求解完之后判断是否大于M


#include <map>
#include <set>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <bitset>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
#define For(i, x, y) for(int i=x;i<=y;i++)
#define _For(i, x, y) for(int i=x;i>=y;i--)
#define Mem(f, x) memset(f,x,sizeof(f))
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%lld",&x)
#define Pri(x) printf("%d\n", x)
#define Prl(x) printf("%lld\n",x)
#define CLR(u) for(int i=0;i<=N;i++)u[i].clear();
#define LL long long
#define ULL unsigned long long
#define mp make_pair
#define PII pair<int,int>
#define PIL pair<int,long long>
#define PLL pair<long long,long long>
#define pb push_back
#define fi first
#define se second
typedef vector<int> VI;
int read(){int x = 0,f = 1;char c = getchar();while (c<''0'' || c>''9''){if (c == ''-'') f = -1;c = getchar();}
while (c >= ''0''&&c <= ''9''){x = x * 10 + c - ''0'';c = getchar();}return x*f;}
const double PI = acos(-1.0);
const double eps = 1e-9;
const int maxn = 1e5 +10;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
int N;
LL M,K;
int a[maxn],b[maxn];
int pre[maxn],id[maxn];
bool check(int x){
for(int i = 1; i <= N ; i ++) b[i] = (a[i] >= x);
LL ans = 0;
for(int i = 1; i <= N ; i ++){
pre[i] = pre[i - 1] + b[i];
if(b[i]) id[pre[i]] = i;
if(pre[i] >= K) ans += id[pre[i] - K + 1];
}
return ans >= M;
}
int solve(){
int l = 0,r = INF;
int ans = INF;
while(l <= r){
int m = l + r >> 1;
if(check(m)){
ans = m;
l = m + 1;
}else{
r = m - 1;
}
}
return ans;
}
int main(){
int T; Sca(T);
while(T--){
scanf("%d%lld%lld",&N,&K,&M);
for(int i = 1; i <= N ; i ++) Sca(a[i]);
Pri(solve());
}
return 0;
}
F.0:11:37 solved by hl
下标为奇数的构造为1,2,3,4,5 ... x
下标为偶数的构造为x + 1,x + 2.. N


#include <map>
#include <set>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <bitset>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
#define For(i, x, y) for(int i=x;i<=y;i++)
#define _For(i, x, y) for(int i=x;i>=y;i--)
#define Mem(f, x) memset(f,x,sizeof(f))
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%lld",&x)
#define Pri(x) printf("%d\n", x)
#define Prl(x) printf("%lld\n",x)
#define CLR(u) for(int i=0;i<=N;i++)u[i].clear();
#define LL long long
#define ULL unsigned long long
#define mp make_pair
#define PII pair<int,int>
#define PIL pair<int,long long>
#define PLL pair<long long,long long>
#define pb push_back
#define fi first
#define se second
typedef vector<int> VI;
int read(){int x = 0,f = 1;char c = getchar();while (c<''0'' || c>''9''){if (c == ''-'') f = -1;c = getchar();}
while (c >= ''0''&&c <= ''9''){x = x * 10 + c - ''0'';c = getchar();}return x*f;}
const double PI = acos(-1.0);
const double eps = 1e-9;
const int maxn = 1e5 + 10;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
int N,M,K;
int a[maxn];
int main(){
int T; Sca(T);
while(T--){
int cnt = 0;
Sca(N);
for(int i = 1; i <= N; i += 2) a[i] = ++cnt;
for(int i = 2; i <= N ; i += 2) a[i] = ++ cnt;
for(int i = 1; i <= N ; i ++){
printf("%d ",a[i]);
}
puts("");
}
return 0;
}
H.3:09:34(-5) solved by gbs
很显然最终状态的最大公因数只要考虑质数就够了
预处理出1e5以下的所有素数,枚举所有素数然后贪心check


#include <iostream>
#include<stack>
#include<math.h>
#include<stdlib.h>
#include<string.h>
#include<string>
#include<ctime>
#include<complex>
#include<stdio.h>
#include<algorithm>
#include<map>
#include<queue>
#include<deque>
using namespace std;
typedef long long LL;
const int mod =1e9+7;
//10*n
const int maxn =1e5+35;
int n;
bool if_p[maxn+15];
int p_list[maxn/2+15];
int an[maxn];
LL sum ;
int p_num =0;
LL fen_list[500];
int fen_num;
LL fin_ans;
void pre()
{
memset(if_p,true,sizeof(if_p));
for (int i=2; i<maxn; i++)
{
if (if_p[i])
{
p_list[p_num++] = i;
//cout<<i<<endl;
for (int j = i<<1; j<maxn; j+= i)
{
if_p[j] =false;
}
}
}
}
void fen(LL n)
{
fen_num =0;
for (int i=0; i<p_num; i++)
{
if (p_list[i]>n)
break ;
if(n%p_list[i] == 0)
{
fen_list[fen_num++] = p_list[i];
while(n%p_list[i] == 0)
n/=p_list[i];
}
}
if (n> 1)
{
fen_list[fen_num++] =n;
}
}
int remain[maxn+15];
void judge(LL a)
{
LL now_time = 0;
LL best_time =0;
int h1;
if (a<= 100000)
{
memset(remain,0,sizeof(int)*(a+4));
for (int i=0; i<n; i++)
{
h1= an[i]%a;
if (h1==0)
continue;
remain[h1]++;
best_time += min(0LL+h1,a-h1);
if (best_time>=(fin_ans<<1))
return ;
}
}
else
{
sort(an,an+n);
int time2 = sum/a;
for (int i=0; i<n-time2; i++)
{
now_time += an[i];
}
fin_ans = min(fin_ans,now_time);
return ;
}
if (a == 2)
{
fin_ans = min(fin_ans,0LL+remain[1]/2);
return ;
}
int lef = 1;
int rif = a-1;//a-1
now_time += 1LL* (a-rif)*remain[rif] + 1LL * lef*remain[lef];
LL now_c = (a-rif)*remain[rif] - 1LL * lef*remain[lef];
while(lef!= rif-1)
{
if (now_c<0)
{
rif--;
now_c += (a-rif)*remain[rif];
now_time += (a-rif)*remain[rif];
}
else
{
lef++;
now_c -= 1LL*lef*remain[lef];
now_time += 1LL*lef*remain[lef];
}
}
LL time1 ;
time1 = abs(now_c)/a;
if (now_c >0)
{
now_time+= time1 * (2*rif-a);
}
else
{
now_time+= time1 * (a-lef-lef);
}
fin_ans = min(fin_ans,now_time/2);
}
/*void judge(LL a)
{
LL now_time = 0;
LL best_time =0;
int h1;
deque<LL>dqu;
if (a<= 100000)
{
memset(remain,0,sizeof(int)*(a+4));
for (int i=0; i<n; i++)
{
h1= an[i]%a;
if (h1==0)
continue;
remain[h1]++;
best_time += min(0LL+h1,a-h1);
if (best_time>=fin_ans<<1)
return ;
}
if (a == 2)
{
fin_ans = min(fin_ans,0LL+remain[1]/2);
return ;
}
for (int i=1; i<a; i++)
{
while(remain[i]--)
{
dqu.push_back(i);
}
}
}
else
{
sort(an,an+n);
for (int i=0; i<n; i++)
{
dqu.push_back(an[i]);
best_time +=min(0LL+an[i],a-an[i]);
if (best_time>=fin_ans<<1)
return ;
}
}
LL t1,t2,t3;
while(!dqu.empty())
{
t1 = dqu.front();
t2 = dqu.back();
dqu.pop_back();
dqu.pop_front();
t3 = min(t1,a-t2);
t1-=t3;
t2+=t3;
now_time += t3;
if (now_time >=fin_ans)
return ;
if (t1!= 0)
dqu.push_front(t1);
if (t2 != a)
dqu.push_back(t2);
}
fin_ans = min(fin_ans,now_time);
}*/
int main()
{
pre();
int t;
cin >>t;
while(t--)
{
cin >>n;
sum =0;
for (int i=0; i<n; i++)
{
scanf("%d",&an[i]);
//an[i] = 100000;
sum += an[i];
}
fin_ans = 1e17;
fen(sum);
if (sum == 0)
{
cout<<0<<endl;
continue;
}
for (int i =0; i<fen_num; i++)
{
//cout<<fen_list[i]<<"D"<<endl;
//cout<<sum<<"S"<<fen_list[i]<<endl;
judge(fen_list[i]);
}
cout<<fin_ans<<endl;
}
return 0;
}
/*
111
5111111 11111116 12133215 251111111
111
5 15 5 25
5 14 5 25
5 13 5 25
5 12 5 25
3
14 14 5 5
14 14 5 5
*/
J. 5:10:01 solved by zcz
HL:他弄了一个很复杂的公式给我敲,至于怎么整出来的,咱也不知道,咱也不敢问


#include <map>
#include <set>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <bitset>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
#define For(i, x, y) for(int i=x;i<=y;i++)
#define _For(i, x, y) for(int i=x;i>=y;i--)
#define Mem(f, x) memset(f,x,sizeof(f))
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%lld",&x)
#define Pri(x) printf("%d\n", x)
#define Prl(x) printf("%lld\n",x)
#define CLR(u) for(int i=0;i<=N;i++)u[i].clear();
#define LL long long
#define ULL unsigned long long
#define mp make_pair
#define PII pair<int,int>
#define PIL pair<int,long long>
#define PLL pair<long long,long long>
#define pb push_back
#define fi first
#define se second
typedef vector<int> VI;
int read(){int x = 0,f = 1;char c = getchar();while (c<''0'' || c>''9''){if (c == ''-'') f = -1;c = getchar();}
while (c >= ''0''&&c <= ''9''){x = x * 10 + c - ''0'';c = getchar();}return x*f;}
const double PI = acos(-1.0);
const double eps = 1e-9;
const int maxn = 110;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
int N,M,K;
LL quick_power(LL a,LL b){
LL ans = 1;
while(b){
if(b & 1) ans = ans * a % mod;
b >>= 1;
a = a * a % mod;
}
return ans;
}
LL inv(LL a){
return quick_power(a,mod - 2);
}
LL x[10],y[10];
LL fac(LL v){
x[1] = 2; y[1] = 2;
x[2] = 3; y[2] = 8;
x[3] = 4; y[3] = 20;
x[4] = 5; y[4] = 40;
x[5] = 6; y[5] = 70;
LL ans = 0;
for(int i = 1; i <= 5; i ++){
LL sum = 1;
for(int j = 1; j <= 5; j ++){
if(i != j) sum = sum * (x[i] + mod - x[j]) % mod;
}
sum = inv(sum);
sum = sum * y[i] % mod;
for(int j = 1; j <= 5; j ++){
if(i != j) sum = sum * (v - x[j] + mod) % mod;
}
ans = (ans + sum) % mod;
}
return ans;
}
LL fac2(LL v){
x[1] = 1; y[1] = 6;
x[2] = 2; y[2] = 30;
x[3] = 3; y[3] = 90;
x[4] = 4; y[4] = 210;
x[5] = 5; y[5] = 420;
LL ans = 0;
for(int i = 1; i <= 5; i ++){
LL sum = 1;
for(int j = 1; j <= 5; j ++){
if(i != j) sum = sum * (x[i] + mod - x[j]) % mod;
}
sum = inv(sum);
sum = sum * y[i] % mod;
for(int j = 1; j <= 5; j ++){
if(i != j) sum = sum * (v - x[j] + mod) % mod;
}
ans = (ans + sum) % mod;
}
return ans;
}
inline LL mul(LL a,LL b){
return a % mod * b % mod;
}
inline LL add(LL a,LL b){
return ((a + b) % mod + mod) % mod;
}
LL S3(LL x){
return x * (x + 1) % mod * x % mod * (x + 1) % mod * inv(2) % mod * inv(2) % mod;
}
LL S1(LL x){
return (x + 1) * x % mod * inv(2) % mod;
}
LL S2(LL x){
return mul(mul(mul(x,add(x,1)),add(2 * x % mod,1)),inv(6));
}
int main(){
int T;
Sca(T);
LL inv2 = inv(2);
while(T--)
{
LL a,b;
scanf("%lld %lld",&a,&b);
long long ans;
LL n = a;
if(b==1)
{
ans = mul(inv2,(add(add(-S3(n),-S2(n)),mul(add(S1(n),S2(n)),n))));
ans = mul(ans,inv(add(mul(S1(n),n),-S2(n))));
}
else
{
ans= mul(mul(inv2,add(S3(n),-S1(n))),inv(add(S2(n),-S1(n))));
}
printf("%lld\n",ans);
}
return 0;
}
L. unsolved by hl
赛后补题 HDU6241 17CCPC哈尔滨L
M.2:56:06(-14) solved by zcz
每次随机找3个点,求出他们的圆心去check是否为最终答案
因为至少一半的点在最终答案的圆上,每次就有1 / 8的概率中奖
因为每次都直接随机点,显然出题人不能构造出让我们TLE的数据


#include<iostream>
#include<cstring>
#include<cstdio>
#include<ctime>
#include<cstdlib>
#include<cmath>
using namespace std;
int random(int n)
{
return (long long)rand()*rand()%n;
}
struct Point
{
double x,y;
Point(double x0=0,double y0=0) : x(x0) , y(y0) { }
friend Point operator-(const Point &a,const Point &b)
{
return Point(a.x-b.x,a.y-b.y);
}
friend Point operator+(const Point &a,const Point &b)
{
return Point(a.x+b.x,a.y+b.y);
}
friend Point operator*(const Point &a,double b)
{
return Point(a.x*b,a.y*b);
}
};
double Cross(Point a,Point b)
{
return a.x*b.y-b.x*a.y;
}
Point getLineIntersection(const Point &P,const Point &v,const Point &Q,const Point &w)
{
Point u=P-Q;
double t=Cross(w,u)/Cross(v,w);
return P+v*t;
}
Point p[100005];
int n;
const double eps=1e-9;
int dcmp(double x)
{
return x>eps||x<-eps;
}
Point Get(Point a,Point b,Point c)
{
Point p1,p2,v1,v2;
p1.x=(a.x+b.x)/2;
p1.y=(a.y+b.y)/2;
p2.x=(a.x+c.x)/2;
p2.y=(a.y+c.y)/2;
v1.x=a.y-b.y;
v1.y=b.x-a.x;
v2.x=a.y-c.y;
v2.y=c.x-a.x;
if(dcmp(v1.x*v2.y-v2.x*v1.y)==0) return Point(0,0);
return getLineIntersection(p1,v1,p2,v2);
}
double dis(Point a,Point b)
{
return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
bool judge(Point T,double R)
{
int cnt=0;
for(int i=0;i<n;i++)
{
if(dcmp(sqrt(dis(T,p[i]))-sqrt(R))==0)
{
cnt++;
}
}
return cnt>=(n+1)/2;
}
void solve()
{
int t1,t2,t3;
if(n<=4)
{
if(n==1)
{
double tt=1;
printf("%lf %lf %lf\n",p[0].x+1,p[0].y,tt);
}
else
{
printf("%.10lf %.10lf %.10lf\n",(p[0].x+p[1].x)/2,(p[0].y+p[1].y)/2,sqrt(dis(p[0],p[1]))/2);
}
return ;
}
while(1)
{
t1=random(n);
do
{
t2=random(n);
}
while(t2==t1);
do
{
t3=random(n);
}
while(t3==t2||t3==t1);
Point T=Get(p[t1],p[t2],p[t3]);
double R=dis(p[t1],T);
double MAX=1e9;
if(sqrt(R)>=MAX||T.x>=MAX||T.x<=-MAX||T.y>=MAX||T.y<=-MAX) continue;
if(judge(T,R))
{
printf("%.10lf %.10lf %.10lf\n",T.x,T.y,sqrt(R));
break;
}
}
}
int main()
{
srand((unsigned)time(NULL));
int T;
cin>>T;
while(T--)
{
cin>>n;
for(int i=0;i<n;i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
}
solve();
}
return 0;
}

2017CCPC 哈尔滨 B
这题没有考虑到m这个东西,所以就没有往二分答案的方向想
二分答案
check的时候,我们找的是大于等于x的数有多少个被加入到那个数组中。如果 >= m说明这个数可能是答案,否则就不是。
用尺取来计数,还算比较好理解。
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 int n,k;
6 long long m;
7
8 int a[100005];
9 int b[100005];
10
11 bool check(int x) {
12
13 long long ans = 0;
14 int num = 0;
15 int pos = 1;
16
17 for(int i = 1; i <= n; i++) {
18 if(a[i] >= x) {
19 num++;
20 }
21 if(num == k) {
22
23 // 后面形成的区间,x作为第k大,或者有比它大的
24 // 但是一定会有n - i + 1个大于等于x的数被加入到ans数组中
25 ans += n - i + 1;
26
27 // 如果左端这个数小于x
28 // 那么去掉他没有影响
29 // 依然会有n - i + 1个大于等于x的数加入到ans数组中
30 while(a[pos] < x) {
31 ans += n - i + 1;
32 pos++;
33 }
34 pos++;
35 num--;
36 }
37
38
39 }
40
41 //cout<<ans<<endl;
42 if(ans >= m) return true;
43 return false;
44 }
45
46 int main() {
47
48 int t;
49 scanf("%d",&t);
50
51 while(t--) {
52 scanf("%d %d %lld",&n,&k,&m);
53
54 for(int i = 1; i <= n; i++) {
55 scanf("%d",&a[i]);
56 }
57
58 //cout<<num<<endl;
59 int L = 1,R = 1000000001;
60 int mid;
61 while(R - L > 1) {
62 mid = L + R >> 1;
63
64 //cout<<mid<<'' ''<<b[mid]<<endl;
65 if(check(mid)) {
66 L = mid;
67 }
68 else {
69 R = mid;
70 }
71 }
72
73
74 printf("%d\n",L);
75
76 }
77
78
79
80
81
82 return 0;
83 }

2020哈尔滨php培训哪里好?

2020年php工程师每个月仍然有数以万计的岗位空缺招聘需求,所以市面上php培训机构也越来越多,那么哈尔滨php培训哪里好?哈尔滨哪个php培训机构好?这就要从以下几点来看:
一、看这个培训机构的社会荣誉与行业地位
真正有实力、专业、靠谱的PHP培训机构除了社会口碑,有公信力,影响力才值得信赖。
二、看课程体系和教材
在课程体系上,我们应当先看课程体系设置的依据。一个好的课程体系,应当实用、具体;应当来源于企业的实际应用,即企业需要什么,就学习什么。再看课程体系内容是否全面、系统。
立即学习“PHP免费学习笔记(深入)”;
三、看学习时长
一共要学多久,包括每天学多少课时,每周学几天等等,一方面表明学习内容的多少,另因方面影响到学习费用。但是有很多PHP培训机构混淆概念,把免费上机的时间也算作了课时,看上去好像学习时间比较长,内容很多,其实并不是这样;还有一些培训机构,本身的课时并不多,但是学习周期很长,看上去同样学习内容较多,
但是实际情况并不是如此。另外,一些培训机构把学习其它课程的内容也安排到了课程当中,这样真正学习技术的课时并不多。所以,同学们还是应该自己计算一下真正的课时数量以及学习周期。
四、看学校和企业的合作关系
培训的最终目的是实现学员顺利就业,培训机构和互联网企业的关系将为学员的就业打下基础,同时和动漫游戏企业的合作也能体现出学校的实力。
五、看就业承诺,看学员输出
培训机构都会对学员作出就业承诺,学员应该对就业承诺作出理性分析,不能仅仅凭工作人员的口头说明作判断。
六、看教学授课方式
学习最好的方式是理论与实践相结合,并在一定的过程中,安排学员亲自动手操作真实的项目。
注:php中文网提供大量免费、原创、高清的php视频教程,并且会定期举行php公益培训!
相关推荐:1.《2020济南php培训机构哪个好?》2.《2020南京php培训机构哪家好?》
以上就是2020哈尔滨php培训哪里好?的详细内容,更多请关注php中文网其它相关文章!
关于哈尔滨手机seo(哈尔滨手机回收)和哈尔滨手机回收电话的介绍已经告一段落,感谢您的耐心阅读,如果想了解更多关于"科林明伦杯" 哈尔滨理工大学第八届程序设计竞赛 题解、2017 CCPC 哈尔滨、2017CCPC 哈尔滨 B、2020哈尔滨php培训哪里好?的相关信息,请在本站寻找。
本文标签:



![[转帖]Ubuntu 安装 Wine方法(ubuntu如何安装wine)](https://www.gvkun.com/zb_users/cache/thumbs/4c83df0e2303284d68480d1b1378581d-180-120-1.jpg)

