[Swift]LeetCode459. 重复的子字符串 | Repeated Substring Pattern（重复字符子串个数计算）

25-04-24 1

如果您对[Swift]LeetCode459.重复的子字符串|RepeatedSubstringPattern和重复字符子串个数计算感兴趣，那么这篇文章一定是您不可错过的。我们将详细讲解[Swift]

如果您对[Swift]LeetCode459. 重复的子字符串 | Repeated Substring Pattern和重复字符子串个数计算感兴趣，那么这篇文章一定是您不可错过的。我们将详细讲解[Swift]LeetCode459. 重复的子字符串 | Repeated Substring Pattern的各种细节，并对重复字符子串个数计算进行深入的分析，此外还有关于(?:pattern)与(?=pattern)的区别、2022-01-17：单词规律 II。给你一种规律 pattern 和一个字符串 str，请你判断 str 是否遵循其相同的规律。这里我们指的是完全遵循，例如 pattern 里的每个字母和字符、459. Repeated Substring Pattern、459. 重复的子字符串(LeetCodet题库)的实用技巧。

本文目录一览：

[Swift]LeetCode459. 重复的子字符串 | Repeated Substring Pattern（重复字符子串个数计算）
(?:pattern)与(?=pattern)的区别
2022-01-17：单词规律 II。给你一种规律 pattern 和一个字符串 str，请你判断 str 是否遵循其相同的规律。这里我们指的是完全遵循，例如 pattern 里的每个字母和字符
459. Repeated Substring Pattern
459. 重复的子字符串(LeetCodet题库)

[Swift]LeetCode459. 重复的子字符串 | Repeated Substring Pattern（重复字符子串个数计算）

Given a non-empty string check if it can be constructed by taking a substring of it and appending multiple copies of the substring together. You may assume the given string consists of lowercase English letters only and its length will not exceed 10000.、

Example 1:

Input: "abab"
Output: True
Explanation: It‘s the substring "ab" twice.

Example 2:

Input: "aba"
Output: False

Example 3:

Input: "abcabcabcabc"
Output: True
Explanation: It‘s the substring "abc" four times. (And the substring "abcabc" twice.)

给定一个非空的字符串，判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母，并且长度不超过10000。

示例 1:

输入: "abab"

输出: True

解释: 可由子字符串 "ab" 重复两次构成。

示例 2:

输入: "aba"

输出: False

示例 3:

输入: "abcabcabcabc"

输出: True

解释: 可由子字符串 "abc" 重复四次构成。 (或者子字符串 "abcabc" 重复两次构成。)

148ms

 1 class Solution {
 2     //kmp算法
 3     func repeatedSubstringPattern(_ s: String) -> Bool {
 4         var arr:[Character] = [Character]()
 5         for char in s.characters
 6         {
 7             arr.append(char)
 8         }
 9         var i:Int = 1
10         var j:Int = 0
11         var n:Int = s.count
12         var dp:[Int] = [Int](repeating:0,count:n + 1)
13         while(i < n)
14         {
15             if arr[i] == arr[j]
16             {
17                 i += 1
18                 j += 1
19                 dp[i] = j
20             }
21             else if j == 0
22             {
23                 i += 1
24             }
25             else
26             {
27                 j = dp[j]
28             }
29         }
30         return dp[n] % (n - dp[n]) == 0 && dp[n] != 0
31     }
32 }

292ms

1 class Solution {
2     func repeatedSubstringPattern(_ s: String) -> Bool {
3         let ss = s + s
4         let str = ss[ss.index(after: ss.startIndex)..<ss.index(before: ss.endindex)]
5         return str.contains(s)
6     }
7 }

480ms

 1 class Solution {
 2     func repeatedSubstringPattern(_ s: String) -> Bool {
 3         let length = s.count
 4         var index  = length / 2
 5 
 6         while index >= 1 {
 7             if length % index == 0 {
 8                 let c = length / index
 9                 var current = ""
10                 
11                 for _ in 0..<c {
12                     
13                     let offset = s.index(s.startIndex,offsetBy: index)
14                     current += String(s[..<offset])
15 
16                 }
17                 if current == s {
18                     return true
19                 }
20 
21             }
22             index -= 1
23         }
24  
25         return false
26     }
27 }

500ms

1 class Solution {
2     func repeatedSubstringPattern(_ s: String) -> Bool {
3         let chas = [Character](s)
4         let res = String(chas[1...]) + String(chas[..<(chas.count-1)])
5         
6         return res.contains(s)
7     }
8 }

604ms

 1 class Solution {
 2     func repeatedSubstringPattern(_ s: String) -> Bool {
 3         let count = s.count
 4         var huff = count / 2
 5         while huff >= 1 {
 6             if count % huff == 0 {
 7                 let toIndex = s.index(s.startIndex,offsetBy: huff)
 8                 let subString = s[s.startIndex..<toIndex]
 9                 
10                 var num = count / huff
11                 var sumString = ""
12                 
13                 while num > 0 {
14                     sumString = sumString + subString
15                     num = num - 1
16                 }
17                 
18                 if sumString == s {
19                     return true
20                 }
21             }
22             
23             huff = huff - 1
24         }
25         return false
26     }
27 }

3292ms

 1 class Solution {
 2     func repeatedSubstringPattern(_ s: String) -> Bool {
 3         let length = s.count
 4         
 5         var result = false;
 6         for index in 1...length {
 7             // 整除则对比
 8             if length % (index) == 0 {
 9                 // 从0到index
10                 let character = s.prefix(index)
11                 let increment = index;
12                 var start = increment;
13                 
14                 var isEqual = false;
15                 while (start < length) {
16                     let begin = s.index(s.startIndex,offsetBy: start)
17                     let stop = s.index(s.startIndex,offsetBy: start + increment)
18                     let temp = s[begin..<stop]
19                     
20                     if (character == temp) {
21                         start += increment;
22                         isEqual = true;
23                         continue;
24                     } else {
25                         isEqual = false;
26                         break;
27                     }
28                 }
29                 result = isEqual;
30                 if isEqual {
31                     break;
32                 }
33             }
34         }
35         return result
36     }
37 }

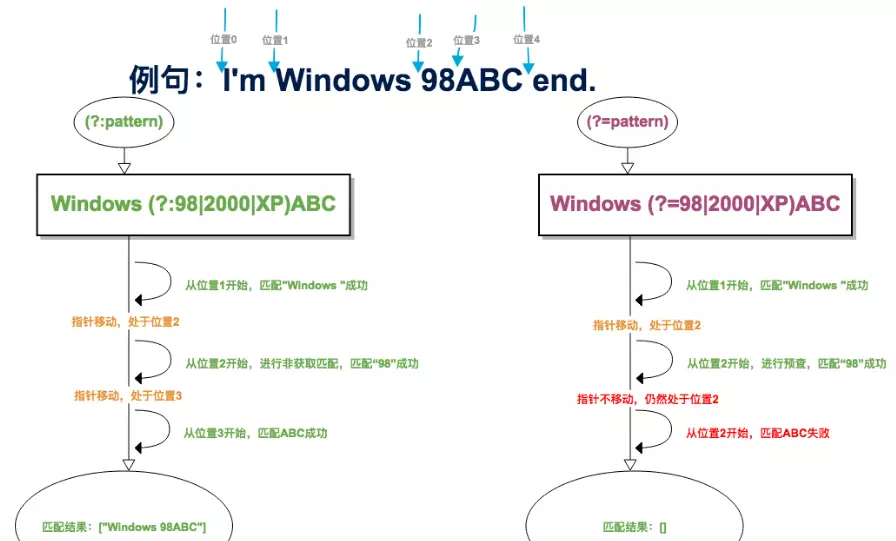
(?:pattern)与(?=pattern)的区别

官方定义

(?:pattern)

匹配 pattern 但不获取匹配结果，也就是说这是一个非获取匹配，不进行存储供以后使用。这在使用 "或" 字符 (|) 来组合一个模式的各个部分是很有用。例如， ''industr(?:y|ies) 就是一个比 ''industry|industries'' 更简略的表达式。

(?=pattern)

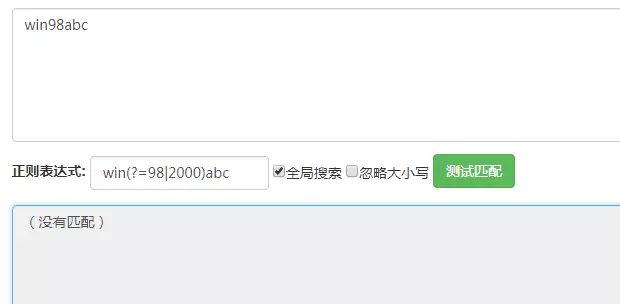
正向肯定预查（look ahead positive assert），在任何匹配pattern的字符串开始处匹配查找字符串。这是一个非获取匹配，也就是说，该匹配不需要获取供以后使用。例如，"Windows(?=95|98|NT|2000)"能匹配"Windows2000"中的"Windows"，但不能匹配"Windows3.1"中的"Windows"。预查不消耗字符，也就是说，在一个匹配发生后，在最后一次匹配之后立即开始下一次匹配的搜索，而不是从包含预查的字符之后开始。

(?!pattern)

正向否定预查(negative assert)，在任何不匹配pattern的字符串开始处匹配查找字符串。这是一个非获取匹配，也就是说，该匹配不需要获取供以后使用。例如"Windows(?!95|98|NT|2000)"能匹配"Windows3.1"中的"Windows"，但不能匹配"Windows2000"中的"Windows"。预查不消耗字符，也就是说，在一个匹配发生后，在最后一次匹配之后立即开始下一次匹配的搜索，而不是从包含预查的字符之后开始。

(?<=pattern)

反向(look behind)肯定预查，与正向肯定预查类似，只是方向相反。例如，"(?<=95|98|NT|2000)Windows"能匹配"2000Windows"中的"Windows"，但不能匹配"3.1Windows"中的"Windows"。

(?<!pattern)

反向否定预查，与正向否定预查类似，只是方向相反。例如"(?<!95|98|NT|2000)Windows"能匹配"3.1Windows"中的"Windows"，但不能匹配"2000Windows"中的"Windows"。

共同点

(?:pattern) 与 (?=pattern)都匹配pattern，但不会把pattern结果放到Matches的集合中。

区别

(?:pattern) 匹配得到的结果包含pattern。
(?=pattern) 则不包含。

对字符串："industry abc"的匹配结果：

industr(?:y|ies) ---> "industry"
industr(?=y|ies) ---> "industr"

是否消耗字符

(?:pattern) 消耗字符，下一字符匹配会从已匹配后的位置开始。
(?=pattern) 不消耗字符，下一字符匹配会从预查之前的位置开始。

即后者只预查，不移动匹配指针。如：

2022-01-17：单词规律 II。给你一种规律 pattern 和一个字符串 str，请你判断 str 是否遵循其相同的规律。这里我们指的是完全遵循，例如 pattern 里的每个字母和字符

2022-01-17：单词规律 II。给你一种规律 pattern 和一个字符串 str，请你判断 str 是否遵循其相同的规律。这里我们指的是完全遵循，例如 pattern 里的每个字母和字符

2022-01-17：单词规律 II。
给你一种规律 pattern 和一个字符串 str，请你判断 str 是否遵循其相同的规律。
这里我们指的是完全遵循，例如 pattern 里的每个字母和字符串 str 中每个非空单词之间，存在着双向连接的对应规律。
力扣 291。

答案 2022-01-17：

递归。str=abcabc，pattern=xx。先让 a=x，再让 ab=x, 再让 abc=x。直到完全匹配为止。

代码用 golang 编写。代码如下：

package main

import "fmt"

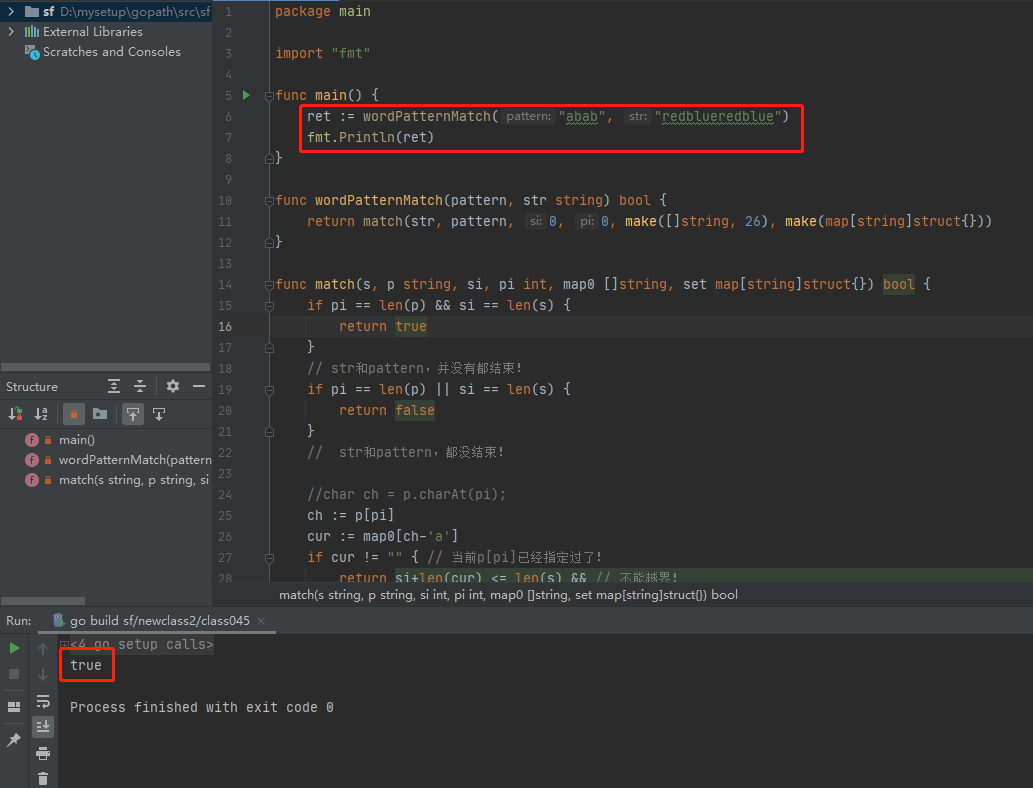
func main() {
   
    ret := wordPatternMatch("abab", "redblueredblue")
    fmt.Println(ret)
}

func wordPatternMatch(pattern, str string) bool {
   
    return match(str, pattern, 0, 0, make([]string, 26), make(map[string]struct{
   }))
}

func match(s, p string, si, pi int, map0 []string, set map[string]struct{
   }) bool {
   
    if pi == len(p) && si == len(s) {
   
        return true
    }
    // str和pattern，并没有都结束！
    if pi == len(p) || si == len(s) {
   
        return false
    }
    // str和pattern，都没结束！

    //char ch = p.charAt(pi);
    ch := p[pi]
    cur := map0[ch-''a'']
    if cur != "" {
    // 当前p[pi]已经指定过了！
        return si+len(cur) <= len(s) && // 不能越界！
            cur == s[si:si+len(cur)] &&
            match(s, p, si+len(cur), pi+1, map0, set)
    }
    // p[pi]没指定！
    end := len(s)
    // 剪枝！重要的剪枝！
    for i := len(p) - 1; i > pi; i-- {
   
        //end -= map0[p[i] - ''a''] == nil ? 1 : len(map0[p[i]-''a''])
        if map0[p[i]-''a''] == "" {
   
            end -= 1
        } else {
   
            end -= len(map0[p[i]-''a''])
        }

    }
    for i := si; i < end; i++ {
   
        // 从si出发的所有前缀串，全试
        cur = s[si : i+1]
        // 但是，只有这个前缀串，之前没占过别的坑！才能去尝试
        if _, ok := set[cur]; !ok {
   
            //set.add(cur);
            set[cur] = struct{
   }{
   }
            map0[ch-''a''] = cur
            if match(s, p, i+1, pi+1, map0, set) {
   
                return true
            }
            map0[ch-''a''] = ""
            //set.remove(cur);
            delete(set, cur)
        }
    }
    return false
}

执行结果如下：

左神 java 代码

459. Repeated Substring Pattern

题目链接：https://leetcode.com/problems...

利用kmp求prefix数组的方法来做，利用string自身的重复性，prefix[i] = k, k < i表示在s[0, i+1]中，最大的k使得s[0, k] == s[i-k+1, i+1]
参考视频：
https://www.youtube.com/watch...

所以如果这个string是呈现repeated substring pattern的样子的话，假设repeat的大小是m，则prefix[0] = prefix[1] = ... = prefix[m-1] = 0 并且prefix[n-1] = prefix[n-2] + 1 =... = prefix[m] + n-m-1 = n - m
根据n % m == 0可知：n%(n - prefix[n-1]) == 0，一旦中间出现不满足pattern的情况，prefix[n-1] < n / 2，所以n-prefix[n-1] > n / 2必然不是n的divisor，如果结尾处少了的话，例如abcabca，虽然prefix[n-1] > n/2，但不满足divisor的条件。

public class Solution {
    public boolean repeatedSubstringPattern(String str) {
        int[] prefix = build(str);
        int n = str.length();
        return prefix[n-1] != 0 && n % (n - prefix[n-1]) == 0;
    }
    
    private int[] build(String s) {
        int n = s.length();
        int[] res = new int[n];
        int i = 1, j = 0;
        while(i < n) {
            // match, add the length
            if(s.charAt(i) == s.charAt(j)) {
                res[i] = j + 1;
                i++; j++;
            }
            // not match, return to previous
            else {
                if(j == 0) i++;
                else j = res[j-1];
            }
        }
        return res;
    }
}

459. 重复的子字符串(LeetCodet题库)

链接：https://leetcode-cn.com/problems/repeated-substring-pattern

给定一个非空的字符串，判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母，并且长度不超过10000。

示例 1:

输入: "abab"

输出: True

解释: 可由子字符串 "ab" 重复两次构成。
示例 2:

输入: "aba"

输出: False
示例 3:

输入: "abcabcabcabc"

输出: True

解释: 可由子字符串 "abc" 重复四次构成。 (或者子字符串 "abcabc" 重复两次构成。)

思路:

给定一个字符串 s ，假如 s为重复X子.........

关于[Swift]LeetCode459. 重复的子字符串 | Repeated Substring Pattern和重复字符子串个数计算的问题就给大家分享到这里，感谢你花时间阅读本站内容，更多关于(?:pattern)与(?=pattern)的区别、2022-01-17：单词规律 II。给你一种规律 pattern 和一个字符串 str，请你判断 str 是否遵循其相同的规律。这里我们指的是完全遵循，例如 pattern 里的每个字母和字符、459. Repeated Substring Pattern、459. 重复的子字符串(LeetCodet题库)等相关知识的信息别忘了在本站进行查找喔。

本文标签：