在这篇文章中，我们将带领您了解[Swift]LeetCode435.无重叠区间|Non-overlappingIntervals的全貌，包括区间无重叠聚类算法的相关情况。同时，我们还将为您介绍有关(n

在这篇文章中，我们将带领您了解[Swift]LeetCode435. 无重叠区间 | Non-overlapping Intervals的全貌，包括区间无重叠聚类算法的相关情况。同时，我们还将为您介绍有关(non-)interactive (non-)login shell、2021-09-28：合并区间。以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals [i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠、352. Data Stream as Disjoint Intervals (TreeMap, lambda, heapq)、497. Random Point in Non-overlapping Rectangles的知识，以帮助您更好地理解这个主题。

• [Swift]LeetCode435. 无重叠区间 | Non-overlapping Intervals（区间无重叠聚类算法）
• (non-)interactive (non-)login shell
• 2021-09-28：合并区间。以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals [i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠
• 352. Data Stream as Disjoint Intervals (TreeMap, lambda, heapq)
• 497. Random Point in Non-overlapping Rectangles

[Swift]LeetCode435. 无重叠区间 | Non-overlapping Intervals（区间无重叠聚类算法）

Input: [ [1,2],[2,3],[3,4],[1,3] ]

Output: 1

Explanation: [1,3] can be removed and the rest of intervals are non-overlapping. 

Input: [ [1,2] ]

Output: 2

Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping. 

Input: [ [1,3] ]

Output: 0

Explanation: You don‘t need to remove any of the intervals since they‘re already non-overlapping.

输入: [ [1,3] ]

输出: 1

解释: 移除 [1,3] 后，剩下的区间没有重叠。

输入: [ [1,2] ]

输出: 2

解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

输入: [ [1,3] ]

输出: 0

解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

76ms

 1 /**
 2  * DeFinition for an interval.
 3  * public class Interval {
 4  *   public var start: Int
 5  *   public var end: Int
 6  *   public init(_ start: Int,_ end: Int) {
 7  *     self.start = start
 8  *     self.end = end
 9  *   }
10  * }
11  */
12 class Solution {
13     func eraSEOverlapIntervals(_ intervals: [Interval]) -> Int {
14         var intervals = intervals
15         if intervals.isEmpty {return 0}
16         intervals.sort(by:{(_ a:Interval,_ b:Interval) -> Bool in return a.start < b.start})
17         var res:Int = 0
18         var n:Int = intervals.count
19         var endLast:Int = intervals[0].end
20         for i in 1..<n
21         {
22             var t:Int = endLast > intervals[i].start ? 1 : 0
23             endLast = t == 1 ? min(endLast,intervals[i].end) : intervals[i].end
24             res += t            
25         }
26         return res
27     }
28 }

 1 /**
 2  * DeFinition for an interval.
 3  * public class Interval {
 4  *   public var start: Int
 5  *   public var end: Int
 6  *   public init(_ start: Int,_ end: Int) {
 7  *     self.start = start
 8  *     self.end = end
 9  *   }
10  * }
11  */
12 class Solution {
13     func eraSEOverlapIntervals(_ intervals: [Interval]) -> Int {
14         if intervals.count <= 1 {
15             return 0
16         }
17         
18         var move = 1
19         var ts = intervals
20         ts.sort { (i1,i2) -> Bool in
21                return i1.end <= i2.end                         
22           }
23 
24         var temp = ts[0]
25         for i in 1..<ts.count {
26             let start = ts[i].start
27             if start >= temp.end {
28                 move += 1
29                 temp = ts[i]
30             }
31         }
32         return intervals.count - move
33     }
34 }

(non-)interactive (non-)login shell

1 login shell

当bash以login shell形式登录的时候，bash会依次执行下列脚本，进行关键全局变量的初始化，如PATH。

1. /etc/profile
2. ~/.bash_profile
3. ~/.bash_login
4. ~/.profile

使用-，-l，--login选项可指定以login shell的形式登录，--noprofile选项可使bash不去执行这些脚本。

当login shell退出的时候，bash会执行如下脚本进行推出前处理：

1. ~/.bash_logout
2. /etc/bash.bash_logout

2 interactive shell

使用-i选项启动interactive shell，该类型的shell读下列脚本进行关键匿名的初始化，如alias ll='ls -l --color=auto'

1. ~/.bashrc

初始化文件可通过--norc选项屏蔽，或--rcfile重新指定

3 注意

/etc/bashrc一般会被/etc/profile，~/.bashrc用到，所以无论是interactive shell还是login shell，该文件的内容都会生效。

4 结论

无论interactive login shell，interactive non-login shell，non-interactive login shell，non-interactive non-login file，不同类型shell的组合其本质区别就在于初始化的脚本运行顺序不同。

5 参考

1. man bash
2. What are the differences between a login shell and interactive shell? - stackoverflow

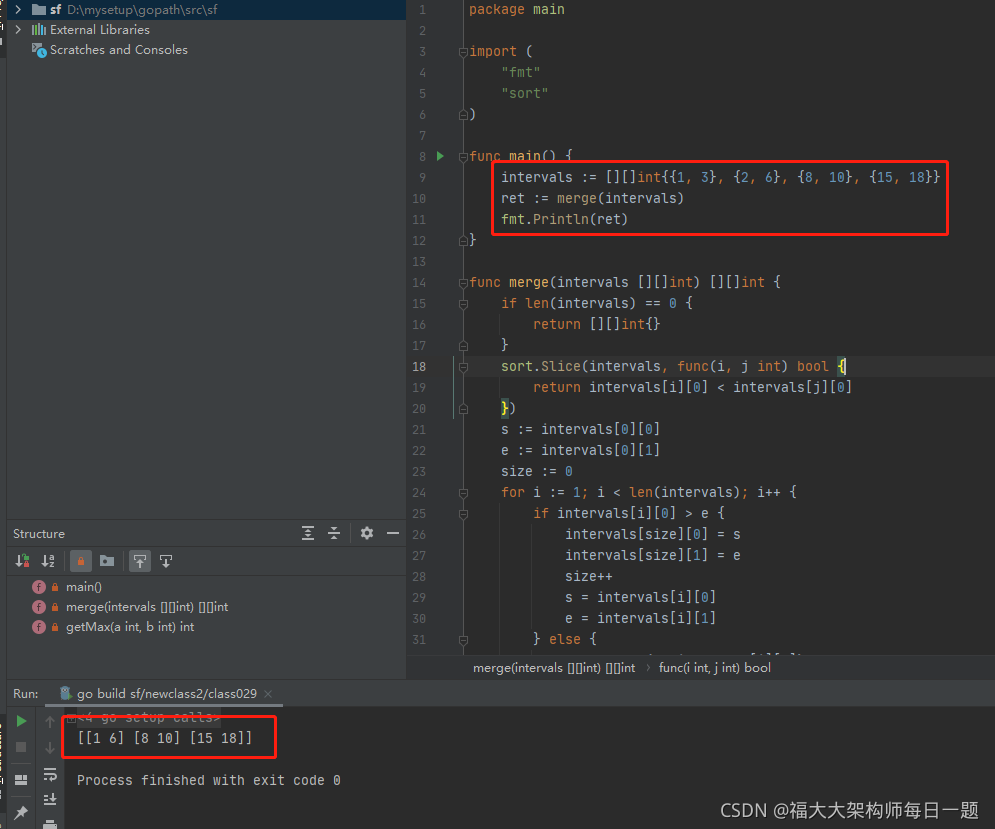
2021-09-28：合并区间。以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals [i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠

2021-09-28：合并区间。以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals [i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。力扣 56。

福大大 答案 2021-09-28：

按开始位置排序。i 的开始位置比之前的结束位置，需要计数。
时间复杂度：排序的。
额外空间复杂度：O (1)。原数组复用。

代码用 golang 编写。代码如下：

package main

import (
    "fmt"
    "sort"
)

func main() {
   
    intervals := [][]int{
   {
   1, 3}, {
   2, 6}, {
   8, 10}, {
   15, 18}}
    ret := merge(intervals)
    fmt.Println(ret)
}

func merge(intervals [][]int) [][]int {
   
    if len(intervals) == 0 {
   
        return [][]int{
   }
    }
    sort.Slice(intervals, func(i, j int) bool {
   
        return intervals[i][0] < intervals[j][0]
    })
    s := intervals[0][0]
    e := intervals[0][1]
    size := 0
    for i := 1; i < len(intervals); i++ {
   
        if intervals[i][0] > e {
   
            intervals[size][0] = s
            intervals[size][1] = e
            size++
            s = intervals[i][0]
            e = intervals[i][1]
        } else {
   
            e = getMax(e, intervals[i][1])
        }
    }
    intervals[size][0] = s
    intervals[size][1] = e
    size++
    return intervals[0:size]
}

func getMax(a int, b int) int {
   
    if a > b {
   
        return a
    } else {
   
        return b
    }
}

执行结果如下：

左神 java 代码

352. Data Stream as Disjoint Intervals (TreeMap, lambda, heapq)

[1, 1]
[1, 1], [3, 3]
[1, 1], [3, 3], [7, 7]
[1, 3], [7, 7]
[1, 3], [6, 7]

Approach #1: C++.

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */
class SummaryRanges {
private:
    vector<Interval> intervals = vector<Interval>();
    
    int binarySearch(vector<Interval> intervals, int val) {
        return binarySearchHelper(intervals, 0, intervals.size(), val);
    }
    
    int binarySearchHelper(vector<Interval> intervals, int start, int end, int val) {
        if (start == end) return -1;
        if (start+1 == end && intervals[start].start < val) return start;
        
        int mid = (start + end) / 2;
        
        if (intervals[mid].start == val) return mid;
        else if (intervals[mid].start < val) 
            return binarySearchHelper(intervals, mid, end, val);
        else 
            return binarySearchHelper(intervals, start, mid, val);
    }
    
public:
    /** Initialize your data structure here. */
    SummaryRanges() {
        
    }
    
    void addNum(int val) {
        int index = binarySearch(intervals, val);
        if (index != -1 && intervals[index].end >= val) 
            return;
        
        if (index != intervals.size() - 1 && val + 1 == intervals[index+1].start)
            intervals[index+1].start = val;
        else if (index != -1 && val - 1 == intervals[index].end) 
            intervals[index].end = val;
        else {
            intervals.insert(intervals.begin()+index+1, Interval(val, val));
        }
        
        if (index != -1 && intervals[index].end + 1 == intervals[index+1].start) {
            intervals[index].end = intervals[index+1].end;
            intervals.erase(intervals.begin()+index+1);
        }
        
        return ;
    }
    
    vector<Interval> getIntervals() {
        return this->intervals;
    }
};

/**
 * Your SummaryRanges object will be instantiated and called as such:
 * SummaryRanges obj = new SummaryRanges();
 * obj.addNum(val);
 * vector<Interval> param_2 = obj.getIntervals();
 */

Approach #2: Java.

/**
 * Definition for an interval.
 * public class Interval {
 *     int start;
 *     int end;
 *     Interval() { start = 0; end = 0; }
 *     Interval(int s, int e) { start = s; end = e; }
 * }
 */
class SummaryRanges {
     TreeMap<Integer, Interval> tree;

    /** Initialize your data structure here. */
    public SummaryRanges() {
        tree = new TreeMap<>();
    }
    
    public void addNum(int val) {
        if (tree.containsKey(val)) return ;
        Integer l = tree.lowerKey(val);
        Integer h = tree.higherKey(val);
        if (l != null && h != null && tree.get(l).end + 1 == val && h == val + 1) {
            tree.get(l).end = tree.get(h).end;
            tree.remove(h);
        } else if (l != null && tree.get(l).end + 1 >= val) {
            tree.get(l).end = Math.max(tree.get(l).end, val);
        } else if (h != null && h == val + 1) {
            tree.put(val, new Interval(val, tree.get(h).end));
            tree.remove(h);
        } else {
            tree.put(val, new Interval(val, val));
        }
    }
    
    public List<Interval> getIntervals() {
        return new ArrayList<>(tree.values());
    }
}

/**
 * Your SummaryRanges object will be instantiated and called as such:
 * SummaryRanges obj = new SummaryRanges();
 * obj.addNum(val);
 * List<Interval> param_2 = obj.getIntervals();
 */

Appraoch #3: Python.

# Definition for an interval.
# class Interval(object):
#     def __init__(self, s=0, e=0):
#         self.start = s
#         self.end = e

class SummaryRanges(object):

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.intervals = []
        

    def addNum(self, val):
        """
        :type val: int
        :rtype: void
        """
        heapq.heappush(self.intervals, (val, Interval(val, val)))
        

    def getIntervals(self):
        """
        :rtype: List[Interval]
        """
        stack = []
        while self.intervals:
            idx, cur = heapq.heappop(self.intervals)
            if not stack:
                stack.append((idx, cur))
            else:
                _, prev = stack[-1]
                if prev.end + 1 >= cur.start:
                    prev.end = max(prev.end, cur.end)
                else:
                    stack.append((idx, cur))
        self.intervals = stack
        return list(map(lambda x : x[1], stack))


# Your SummaryRanges object will be instantiated and called as such:
# obj = SummaryRanges()
# obj.addNum(val)
# param_2 = obj.getIntervals()

Note:

Java -----> Treemap.

Python -----> lambda.

当我们在传入函数时，有些时候，不需要显式地定义函数，直接传入匿名函数更方便。

在 Python 中，对匿名函数提供了有限支持。还是以 map() 函数为例，计算 f (x)=x2 时，除了定义一个 f(x) 的函数外，还可以直接传入匿名函数：

>>> list(map(lambda x: x * x, [1, 2, 3, 4, 5, 6, 7, 8, 9])) [1, 4, 9, 16, 25, 36, 49, 64, 81] 

通过对比可以看出，匿名函数 lambda x: x * x 实际上就是：

def f(x):
    return x * x 

关键字 lambda 表示匿名函数，冒号前面的 x 表示函数参数。

匿名函数有个限制，就是只能有一个表达式，不用写 return，返回值就是该表达式的结果。

用匿名函数有个好处，因为函数没有名字，不必担心函数名冲突。此外，匿名函数也是一个函数对象，也可以把匿名函数赋值给一个变量，再利用变量来调用该函数：

>>> f = lambda x: x * x
>>> f
<function <lambda> at 0x101c6ef28> >>> f(5) 25 

同样，也可以把匿名函数作为返回值返回，比如：

def build(x, y):
    return lambda: x * x + y * y 

Python -----> heapq.

This module provides an implementation of the heap queue algorithm, also known as the priority queue algorithm.

Heaps are arrays for which heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2] for all k, counting elements from zero. For the sake of comparison, non-existing elements are considered to be infinite. The interesting property of a heap is that heap[0] is always its smallest element.

The API below differs from textbook heap algorithms in two aspects: (a) We use zero-based indexing. This makes the relationship between the index for a node and the indexes for its children slightly less obvious, but is more suitable since Python uses zero-based indexing. (b) Our pop method returns the smallest item, not the largest (called a “min heap” in textbooks; a “max heap” is more common in texts because of its suitability for in-place sorting).

These two make it possible to view the heap as a regular Python list without surprises: heap[0] is the smallest item, and heap.sort() maintains the heap invariant!

To create a heap, use a list initialized to [], or you can transform a populated list into a heap via function heapify().

497. Random Point in Non-overlapping Rectangles

1. 问题

给定一系列不重叠的矩形，在这些矩形中随机采样一个整数点。

2. 思路

（1）一个矩形的可采样点个数就相当于它的面积，可以先依次对每个矩形的面积累加存起来（相当于概率分布中的分布累积函数CDF，Cumulative Distribution Function）。 （2）从 [1, 总面积] 中随机取一个数n（面积），表示要取第几个点，找到这个点即可完成题目要求的随机采样。 （3）找点可以先使用python的bisect_left方法，根据这个数（面积）在多个累加面积之间寻找合适的位置（第几个矩形）。然后根据这个数（面积）在那个矩形里找到这个点。 （4）bisect_left的作用是对已排序数组，查找目标数值将会插入的位置并返回（但是不会插入），数值相同时返回靠左的位置。

init：时间复杂度O(n)，空间复杂度O(n) pick：时间复杂度O(n)，空间复杂度O(1)

3. 代码

import random
import bisect

class Solution(object):
    def __init__(self, rects):
        """
        :type rects: List[List[int]]
        """
        self.rects = rects
        sums = 0
        self.accumulate = []
        for x1, y1, x2, y2 in rects:
            sums += (y2 - y1 + 1) * (x2 - x1 + 1)
            self.accumulate.append(sums)

    def pick(self):
        """
        :rtype: List[int]
        """
        n = random.randint(1, self.accumulate[-1])
        i = bisect.bisect_left(self.accumulate, n)
        x1, y1, x2, y2 = self.rects[i]
        if(i > 0):
            n -= self.accumulate[i - 1]
        n -= 1
        return [x1 + n % (x2 - x1 + 1), y1 + n / (x2 - x1 + 1)]

# Your Solution object will be instantiated and called as such:
# obj = Solution(rects)
# param_1 = obj.pick()

4. 类似题目

528. Random Pick with Weight

关于[Swift]LeetCode435. 无重叠区间 | Non-overlapping Intervals和区间无重叠聚类算法的问题我们已经讲解完毕，感谢您的阅读，如果还想了解更多关于(non-)interactive (non-)login shell、2021-09-28：合并区间。以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals [i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠、352. Data Stream as Disjoint Intervals (TreeMap, lambda, heapq)、497. Random Point in Non-overlapping Rectangles等相关内容，可以在本站寻找。